Базовые логические элементы и синтез на их основе минимизированных функционально-устойчивых комбинационных схем

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ РАДИОФИЗИКИ И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ

Кафедра интеллектуальных систем

В. С. Садов

Н. Н. Щетько

ИНТЕГРАЛЬНАЯ
ЭЛЕКТРОНИКА

Лабораторный практикум
для студентов специальностей:

1-31 04 02 «Радиофизика»,
1-31 04 03 «Физическая электроника»,
1-31 04 04 «Аэрокосмические радиоэлектронные
и информационные системы и технологии»,
1-98 01 01 «Компьютерная безопасность»

Направление специальности:
1-98 01 01-02 «Радиофизические методы
и программно-технические средства»,

1-31 03 07 «Прикладная информатика»

Направление специальности:
1-31 03 07-02 «Информационные технологии телекоммуникационных систем»

МИНСК

2014

УДК 621.382.049.77(076.5)

ББК 32.85я7

С14

Рекомендовано
советом факультета радиофизики и компьютерных технологий
27 июня 2014 г., протокол № 11

Лабораторный практикум содержит основные сведения и лабораторные задания по части учебного курса «Интегральная электроника», и предназначен для студентов специальностей «Радиофизика», «Физическая электроника», «Компьютерная безопасность», «Прикладная информатика» и «Аэрокосмические радиоэлектронные и информационные системы и технологии».

Цель издания – изучение принципов построения и функционирования основных микроэлектронных элементов и устройств цифровой и аналоговой электроники, на базе компьютерной программы “EWM 5.12” (Среда моделирования “Electronics Work-bench” (EWB) 5.12. Руководство пользователю) ”, а также получение практических навыков по созданию электронных устройств и анализу их работы.

УДК 621.382.049.77(076.5)

ББК 32.85я7

ã Садов В. С.,

Щетько Н. Н., 2014

ã БГУ, 2014

Лабораторная работа № 1

БАЗОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
И СИНТЕЗ НА ИХ ОСНОВЕ МИНИМИЗИРОВАННЫХ
ФУНКЦИОНАЛЬНО-УСТОЙЧИВЫХ
КОМБИНАЦИОННЫХ СХЕМ

Цель работы: изучение логических возможностей элементов И–НЕ, ИЛИ–НЕ их назначение и освоение процедуры логического синтеза минимизированных алгоритмически устойчивых комбинационных схем и их аналитическое и экспериментальное исследование.

Логические элементы относятся к комбинационным схемам – дискретным автоматам без памяти. Сигналы на выходах комбинационного устройства определяются сочетанием сигналов на входах, и не зависят от их предыдущих состояний.

Математический аппарат, описывающий поведение цифровых схем базируется на алгебре логики. Предметом рассмотрения алгебры логики является утверждение, которое может быть либо истинным, либо ложным. Принято «истинно» обозначать цифрой 1, «ложно» – цифрой 0.

Простейших логических операций три: отрицание (инверсия операция НЕ), логическое умножение (конъюнкция, операция И) и логическое сложение (дизъюнкция, операция ИЛИ). Операция отрицания выполняется над одной переменной и характеризуется следующими свойствами: функция Y=1 при аргументе Х=0 и Y=0, если Х=1. Обозначается отрицание чертой над переменной Х, с которой производится операция 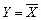(игрек равен не икс); в EWB обозначается как Y=Х'. Соответственно операция логического умножения Y=Х₁Х₂ для двух переменных выражается следующим образом: 0·0=0; 0·1=0; 1·0=0; 1·1=1. Операция логического сложения Y=Х₁ÚХ₂ или Y=Х₁+Х₂ двух переменных характеризуется следующими свойствами: 0+0=0; 0+1=1; 1+0=1; 1+1=1. Операции логического умножения и сложения могут быть распространены и на большее число переменных.

Функция называется булевой или логической (ЛФ), если она сама и ее аргументы принимают значения из множества {0, 1}.

Функция m переменных, определенная на всех 2^m их возможных наборах, называется полностью определенной. Если ЛФ не определена на некоторых наборах, то она называется недоопределенной, а эти наборы называют запрещенными.

Функциональная полнота логических элементов

Функционально полной системой (ФПС) логических элементов (ЛЭ) или элементным базисом, называется такой набор ЛЭ, на базе которого можно построить логическую схему любой сложности. Базис считается минимальным, если удаление хотя бы одного из входящих в него ЛЭ превращает его в функционально неполный. ФПС, состоящая из элементов НЕ, И, ИЛИ, не является минимальной, так как исключением из нее элементов либо И, либо ИЛИ получаются минимальные базисы И–НЕ, ИЛИ–НЕ соответственно. На рис. 1.1 показана реализация логических операций И, ИЛИ, НЕ в базисе И–НЕ.

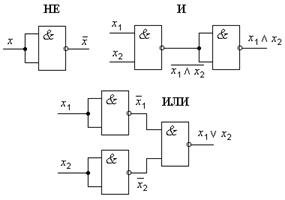
Рис. 1.1

Способы представления ЛФ. Булева функция может быть задана (представлена) словесно, таблично, аналитически, с помощью карт Карно.

Словесно описываются только простые ЛФ.

При табличном способе ЛФ задается таблицей истинности, в которой указаны все возможные наборы переменных и соответствующие им значения функции.

Аналитически (в виде формул) ЛФ может быть записана в совершенной дизъюнктивной нормальной форме (СДНФ) и в совершенной конъюнктивной нормальной форме (СКНФ).