Информационная карта к уроку
Тема: Действительные числа.
1. Теоретический минимум.
Числа, которые представляются бесконечной непериодической дробью, будем называть иррациональными.
Множество иррациональных чисел обозначим I.
Для иррациональных чисел нет единой формы обозначения. Отметим два иррациональных числа, которые обозначаются буквами – это числа π и е.
 | |||
 | |||
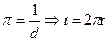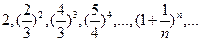Число e :
• 
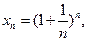Если рассмотреть числовую последовательность:
с общим членом последовательности
то с ростом n значения будут возрастать, но никогда не будет больше 3.
• Это означает, что последовательность ограничена.
• Такая последовательность имеет предел, который равен числу е.
 |
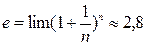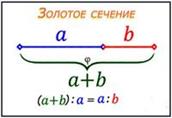Золотое сечение (золотая пропорция, гармоническое деление, деление в крайнем и среднем отношении) — соотношение числовых величин в математике и искусстве: отношение суммы двух величин к большей из них равно отношению большей величины к меньшей (рис. 1).
Золотое сечение (отношение) — иррациональное число, приблизительно равное 1.6180339887.
Т. е. равенство вида (a + b):a = a : b, или, в других обозначениях, равенство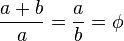 
(часто читается как: «(a + b) относится к a так же, как a относится к b»). Если (a + b):a = a : b, то (a + b) и b называют крайними, а a — средними членами пропорции.
Где:
- (a + b) — весь отрезок (крайний член)
- a — большая её часть(средний)
- b — меньшая её часть(крайний)
Золотое сечение часто обозначается греческой буквой —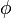 
.
 |
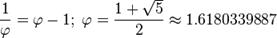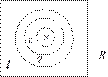
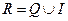Множество вещественных чисел – это объединение множества иррациональных и рациональных чисел.
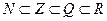Вывод:
Определение модуля действительного числа:
1) 
Пусть на числовой оси точка А имеет координату а. Расстояние от точки начала отсчета О до точки А называется модулем вещественного числа а и обозначается |a|.
 | |||
 | |||
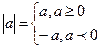2) Раскрытие модуля происходит по правилу:
Свойства модуля:
1.
 | ||
 | ||
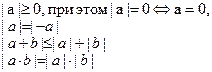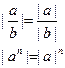2.
3.
4.
5.
6.
 |
2. Выполнение упражнений:
3. 
Самостоятельная работа.
1 вариант:
 |
2 вариант:
4. Домашнее задание: стр. 12, упр. 1 - 6