Работа №2: Определение коэффициентов линейной зависимости.
Необходимо найти коэффициенты a и b в эмпирической зависимости 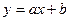 по данным
по данным 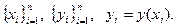
Рассмотрим два способа вычисления данных коэффициентов.
А) Метод средних значений. Считая, что числа 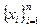 упорядочены, делим все уравнения
упорядочены, делим все уравнения 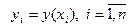 на две равные части (или почти равные). Складывая уравнения каждой части, получаем два уравнения, которые решаем относительно а и в:
на две равные части (или почти равные). Складывая уравнения каждой части, получаем два уравнения, которые решаем относительно а и в:
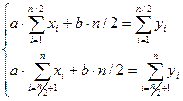 .
.
Б) Метод наименьших квадратов. В данном случае a и b выбираем из условия минимальности выражения 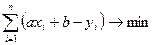 .
.
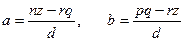 , где
, где
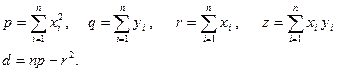
Задача 1.
Зависимость энергии активации от температуры задана таблицей:
| T | T1 | T2 | T3 | … | Tn |
| E | E1 | E2 | E3 | … | En |
Предполагая, что справедливо соотношение 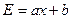 , где
, где 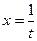 , определить коэффициенты а и b.
, определить коэффициенты а и b.
Задача 2.
Зависимость концентрации от времени в реакции первого порядка задается таблицей:
| T | T1 | T2 | T3 | … | Tn |
| C | C1 | C2 | C3 | … | Cn |
На основании предположения, что 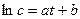 , определить коэффициенты а и b.
, определить коэффициенты а и b.
Задача 3.
Зависимость константы скорости реакции от температуры задана таблицей:
| T | T1 | T2 | T3 | … | Tn |
| К | К1 | К2 | К3 | … | Кn |
Предполагая, что данная зависимость имеет вид 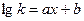 , где
, где 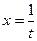 , определить коэффициенты а и b.
, определить коэффициенты а и b.
Замечание.
Выходная информации в задачах лабораторной работы должна содержать исходную таблицу, вид эмпирической зависимости с подставленными вычисленными значениями коэффициентов.
Работа №3: Вычисление определенных интегралов.
Указанные в работе задачи приводят к необходимости вычисления определенных интегралов по одной из квадратурных формул. Приведем простейшие формулы численного интегрирования, которые можно использовать для решения этих задач.
А) Формула трапеций.
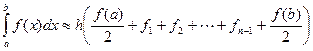 , где
, где 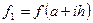 ,
, 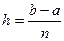 .
.
Б) Формула Симпсона.
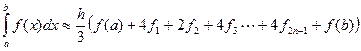 , где
, где 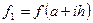 ,
, 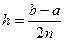 .
.
В) Формула прямоугольников.
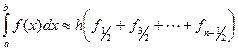 , где
, где 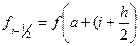 ,
, 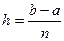
Задача 1. Приведенная свободная энтальпия термохимической системы определяется выражением:
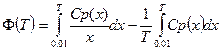 , где Т – абсолютная температура, Ср(х) – теплоемкость при температуре х,
, где Т – абсолютная температура, Ср(х) – теплоемкость при температуре х, 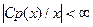 при всех х>0. Используя одну из квадратурных формул, вычислить приведенную свободную энтальпию при заданной температуре Т>0, считая теплоемкость заданной функцией.
при всех х>0. Используя одну из квадратурных формул, вычислить приведенную свободную энтальпию при заданной температуре Т>0, считая теплоемкость заданной функцией.
Задача 2. Вычислить величину f летучести газа при заданном давлении р, используя соотношение
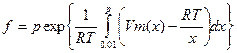 , где Т – абсолютная температура, R – универсальная газовая постоянная. Функция Vm(x), представляющая собой мольный объем реального газа при давлении х, считается известной.
, где Т – абсолютная температура, R – универсальная газовая постоянная. Функция Vm(x), представляющая собой мольный объем реального газа при давлении х, считается известной.
Задача 3. Вычислить интегральное среднее некоторого параметра C химического процесса (скорости реакции, теплоемкости, активности ионов и т.п.) за время (0, Т), используя формулу:
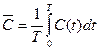 , где C(t) – заданная функция, описывающая поведение указанного параметра во времени.
, где C(t) – заданная функция, описывающая поведение указанного параметра во времени.
Работа №4: Приближенное вычисление производных.
Для решения задач раздела требуется использовать формулы численного дифференцирования для приближенного вычисления производных от функции f(x), заданной таблицей своих значений при дискретных значениях аргумента: 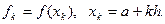
Приведем несколько таких формул.
А) Первая трехточечная формула
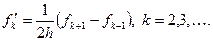
б) Вторая трехточечная формула
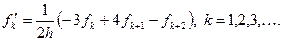
в) Четырехточечная формула
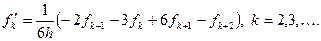
Примечание:
При вычислении производной в левой крайней точке необходимо пользоваться формулой б), в правых крайних точках можно пользоваться упрощенной формулой
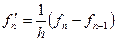
Задача 1.
Зависимость константы равновесия реакции от температуры задана таблицей:
| T | T1 | T2 | T3 | … | Tn |
| Кр | Кр1 | Кр2 | Кр3 | … | Крn |
где Тк+1=Тк+h.
Вычислить тепловой коэффициент реакции 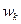 при различных значениях температуры, используя соотношение (к = 1, 2,…., n):
при различных значениях температуры, используя соотношение (к = 1, 2,…., n):
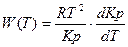 .
.
Задача 2.
Изменение концентрации соли в растворе описывается известной функцией 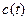 , где t –время. Вычислить значение скорости растворения
, где t –время. Вычислить значение скорости растворения 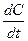 в n точках
в n точках 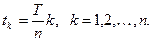
Задача 3.
Вычислить константу скорости реакции k для различных моментов времени 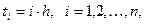 учитывая, что для реакций типа
учитывая, что для реакций типа 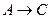 она определяется формулой
она определяется формулой 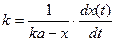 , где
, где 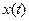 - известная зависимость концентрации вещества А от времени, ka – исходная концентрация вещества А.
- известная зависимость концентрации вещества А от времени, ka – исходная концентрация вещества А.
Замечание.
Выходная информация в задачах раздела должна иметь вид:
Расчет скорости растворения
| время | T1 | T2 | T3 | … | Tn |
| концентрация | С1 | С2 | С3 | … | Сn |
| скорость | DC1 | DC2 | DC3 | … | DCn |








