Примеры решения задач

Дата: 2025-06-02; Просмотры: 10

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

1. Основы молекулярно-кинетической теории

Основные положения молекулярно-кинетической теории и их опытное обоснование. Броуновское движение. Движение и взаимодействие атомов и молекул вещества. Зависимость скорости движения атомов и молекул от температуры. Диффузия. Количество вещества. Постоянная Авогадро. Молярная масса. Число молекул. Масса вещества. Масса и размеры атомов и молекул. Концентрация. Силы взаимодействия молекул. Скорость молекул газа. Средняя квадратичная скорость теплового движения молекул. Распределение молекул по скоростям. Опыт Штерна. Температура и тепловое равновесие. Измерение температуры (термометры). Абсолютная температура. Абсолютный нуль. Молекулярно-кинетический смысл температуры. Постоянная Больцмана. Тепловое расширение твердых и жидких тел.

2. Основы молекулярно-кинетической теории идеального газа

Свойства газов. Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа (вывод). Давление газа. Уравнение состояния идеального газа. Универсальная газовая постоянная. Изопроцессы в газах. Газовые законы. Закон Авогадро. Закон Дальтона.

§1. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ

Краткие теоретические сведения

Закон Авогадро. В равных объемах газа при одинаковых давлениях и температурах находится одинаковое число молекул.

Из закона Авогадро следует: один моль любого газа при одинаковых условиях занимает одинаковый объем. В том числе при нормальных условиях объем 1 моля любого газа равняется 22,4 л.

Нормальные условия:

р = 1,01·10⁵ Па = 0,101 МПа = 760 мм рт. ст., T = 273 K (0 ).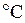

Число Авогадро 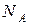– это физическая постоянная, которая численно равна количеству специфицированных структурных единиц в 1 моле вещества. Определяется как количество атомов в 12 граммах чистого изотопа углерода-12. CODATA (Committee on Data for Science and Technology – Комитет по данным для науки и техники) рекомендует следующее значение числа Авогадро:

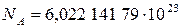моль^–1.

Количеством вещества называется физическая величина, характеризующая количество однотипных структурных единиц (молекул, атомов), содержащихся в веществе, и численно равная

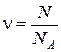, (1.1)

где 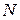– число структурных элементов (молекул, атомов).

Молярная масса вещества – масса одного моля вещества, т. е.

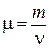, (1.2)

где 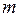– масса вещества, 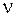– количество вещества.

Массу одной молекулы m₀ можно найти как

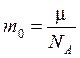Зависимость давления 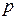газа от концентрации 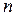молекул и температуры :

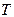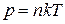, (1.3)

где 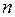– концентрация молекул, 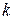= 1,3806·10^–23 Дж/К – постоянная Больцмана, 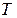– абсолютная температура газа.

Основное уравнение молекулярно-кинетической теории газов (уравнение Клаузиуса): давление газа численно равно двум третям средней кинетической энергии 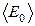поступательного движения всех молекул в единице объема:

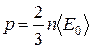. (1.4)

Средняя кинетическая энергия жесткой молекулы:

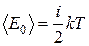, (1.5)

где 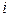– сумма поступательных и вращательных степеней свободы.

Числом степеней свободы молекулы называют количество независимых параметров, с помощью которых можно однозначно задать положение и ориентацию молекулы в пространстве.

Теорема Больцмана о равномерном распределении энергии по степеням свободы: на каждую степень свободы поступательного и вращательного движений приходится в среднем одинаковое количество энергии, равное 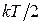. Для одноатомного газа 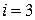, для жестких молекул двухатомного газа 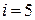, трех- и более атомных газов .

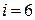Для идеального газа средняя квадратичная скорость определяется

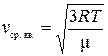. (1.6)

Основное уравнение молекулярно-кинетической теории газов (уравнение Клаузиуса) справедливо лишь для идеального газа, так как в процессе его вывода не учитывается взаимодействие молекул на расстоянии, столкновения молекул рассматриваются как удары упругих шариков. Поэтому уравнение (1.3) и связанное с ним (1.6) применяются лишь для разреженных газов и паров.

Примеры решения задач

Задача 1.1. В озеро, имеющее среднюю глубину 10 м и площадь поверхности 20 км², бросили кристаллик поваренной соли массой 0,01 г. Сколько молекул этой соли оказалось бы в наперстке воды объемом 2 см³, зачерпнутом из озера, если полагать, что соль, растворившись, равномерно распределилась во всем объеме воды?

Решение. Для химических элементов молярной массой является масса одного моля отдельных атомов этого элемента. В этом случае молярная масса элемента, выраженная в г/моль, численно совпадает с массой атома элемента, выраженной в а.е.м. (атомная единица массы). Однако надо чётко представлять разницу между молярной массой и молекулярной массой, понимая, что они равны лишь численно и отличаются по размерности.

Молярные массы сложных молекул можно определить, суммируя молярные массы входящих в них элементов. Тогда для нахождения молярной массы молекулы поваренной соли NaCl необходимо определить молярную массу натрия и молярную массу хлора, используя периодическую таблицу химических элементов Д.И. Менделеева, т. е.

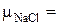
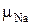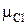+ = 35·1 + 23·1 = 58 (г/моль).

Один моль любого вещества содержит 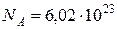моль^–1 частиц (число Авогадро). Одна молекула поваренной соли имеет массу:

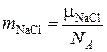Количество молекул в кристалле соли массой m:

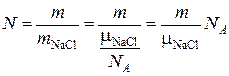Объем озера найдем, умножив его площадь S = 20 км² = 2·10¹¹ см² на его глубину h = 10 м = 10³ см:

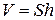Тогда количество молекул соли, находящихся в 1 см³ воды:

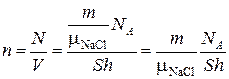Количество молекул в наперстке объемом V_Н:

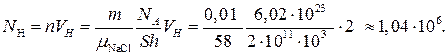
Обратите внимание, что при растворении в большом озере очень маленького количества соли (0,01 г), в наперстке воды окажется миллион молекул соли.

Задача 1.2. Кубическая кристаллическая решетка золота содержит один атом золота на элементарный куб. Плотность золота 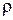= 19320 кг/м³, атомная масса А = 0,197 кг/моль. Определите расстояние между ближайшими атомами золота.

Решение. Решёткой является совокупность точек (атомов), которые обладают замечательным свойством: относительно каждой точки все остальные расположены совершенно одинаково. Для удобства анализа обычно точки решётки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с центрами молекул. Таким образом, объем золота можно вычислить по формуле 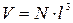, где l – расстояние между ближайшими атомами.

Плотность золота 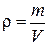, где масса золота т = т₀ · N (т₀ – масса одного атома, N – число атомов). Масса одного атома

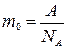т. е. плотность

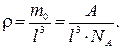
Откуда

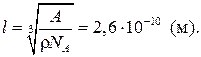
Задача 1.3. Какое давление на стенки сосуда производит кислород, если средняя квадратичная скорость его молекул 400 м/с и концентрация 2,7·10¹⁹ см^–3?

Решение. Воспользуемся периодической таблицей химических элементов Д.И. Менделеева. В молекуле кислорода два атома кислорода, каждый массой 16 а.е.м. Следовательно, молярная масса кислорода:

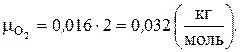
Один моль любого вещества содержит 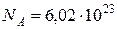моль^–1 частиц (число Авогадро). Одна молекула кислорода имеет массу:

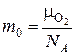Согласно основному уравнению молекулярно-кинетической теории, давление газа с массой молекул 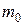, средней квадратичной скоростью 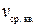и концентрацией (количество молекул в единице объема) n = 2,7 · 10¹⁹ частиц/см³= 2,7·10²⁵ частиц/м³:

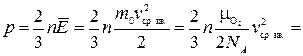
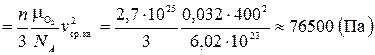Задача 1.4. Средняя квадратичная скорость молекул газа около 400 м/с. Определите объем газа при среднем давлении 1·10⁵ Н/м² и массе 1,0 кг.

Решение. Среднюю квадратичную скорость движения молекул найдем из связи давления газа со средней кинетической энергией молекул:

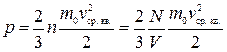Произведение массы одной молекулы на концентрацию молекул (число молекул в единице объема) n равно массе молекул, заключенных в единице объема, т. е. плотности газа 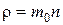. Следовательно, основное уравнение молекулярно-кинетической теории можно записать в виде:

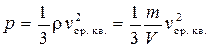Отсюда найдем объем газа:

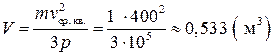ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.5. Найти массу 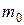атома водорода и гелия.

1.8. Кубическая кристаллическая решетка железа содержит один атом железа на элементарный куб, повторяя который, можно получить всю решетку кристалла. Определить расстояние между ближайшими атомами железа, если плотность железа ρ = 7,9 г/см³, атомная масса железа А = 56 г/моль.

1.10. Современные вакуумные насосы позволяют получать давления до 4 ^. 10^–10 атм (при комнатной температуре). Найти число молекул газа в 1 см³ и среднее расстояние между ними при этом давлении.

1.17. В сосуде объемом 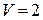л находится 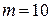г кислорода под давлением 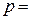8·10⁴ Па. Найти: а) среднюю квадратичную скорость молекул 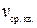; б) количество молекул в сосуде; в) плотность газа.

1.24. Альпинист при каждом вдохе поглощает 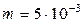кг воздуха. Какой объем воздуха должен вдыхать альпинист в горах, где давление воздуха равняется 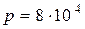Па при температуре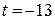 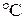? Сколько молекул он выдыхает за один раз? Найти их концентрацию.