Тема 6. Линии второго порядка.
Вопросы для обсуждения:
Окружность. Эллипс. Парабола. Гипербола.
Тематика рефератов: Поверхности 2-порядка.
Задачи.
1. Написать уравнение окружности с центром C(-2; 3) и радиусом, равным 5. Построить окружность. Определить принадлежность точек M1(2; 6), M2(1; 7), М3(0; 4) окружности.
2. Найти координаты центра и радиус окружности х2 + у2 - 8х + 6у - 11 = 0. Построить окружность.
Р е ш е н и е. Сгруппируем члены, содержащие переменные х и y, и дополним каждую группу до полного квадрата суммы или разности:
х2 – 8 x + 16 – 16+у2 + 6 y + 9- 9 - 11 = 0,
или
( x - 4)2 + ( y + З)2 — 36.
Откуда получаем координаты центра С(4; -3) и радиус R = 6. После этого может быть построена окружность.
3. Найти координаты центра и радиус окружности х2 + у2+4х-4y- 1 = 0.
4. Построить окружности:
а) х2 + у2 + 2х -3 = 0;
б) х2 + у2 - 8х + 6у = 0;
в) х2 + у2 + 10 x - 4у + 13 = 0.
5. Написать уравнение окружности, касающейся осей координат и проходящей через точку М1(2; 1).
6. Составить уравнение окружности, проходящей через точки M1(1; 2), М2(0; -1), М3(-3; 0).
7. Составить уравнение окружности, проходящей через точки M1(7; 7),
М2(-2; 4), если ее центр лежит на прямой 2х-у-2 = 0.
8. Определить траекторию точки М, которая при своем движении остается втрое ближе к точке М1(1; 0), чем к прямой х = 9.
9. Определить траекторию точек М, расстояния которых до точки А(0; 1) в 2 раза меньше расстояний до прямой у- 4 = 0.
10. Написать уравнение эллипса, если сумма фокальных радиусов равна 2 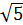 , а фокусы расположены в точках F 1 (-2; 0 ), F 2 (2;0).
, а фокусы расположены в точках F 1 (-2; 0 ), F 2 (2;0).
11. Построить кривые:
а) х2 + 4у2 - 6х +8у = 3;
б) х2 + 2у2 - 4х + 4у + 2 = 0.
12. Построить гиперболы:
а) 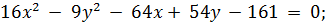
б) 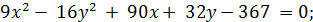
в) 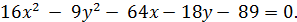
13. Построить параболы:
а) 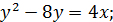
б) 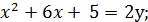
в) 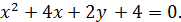
Тема 7. Комплексные числа.
Вопросы для обсуждения:
Комплексные числа. Модуль и аргумент комплексного числа. Формы записи комплексных чисел. Операции над комплексными числами. Формула Муавра-Лапласа. Алгебраические уравнения. Основная теорема алгебры.
Задачи.
1. Выполнить указанные действия:
a) (2 + 3 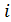 ) + (4 – 7
) + (4 – 7 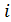 ); б) (1 –
); б) (1 – 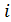 )(3 + 2
)(3 + 2 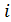 ); в)
); в) 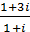 .
.
Решение.
а) (2 + 3 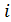 ) + (4 – 7
) + (4 – 7 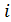 ) = (2 + 4) + (3 – 7)
) = (2 + 4) + (3 – 7) 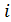 = 6 - 4
= 6 - 4 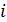 ;
;
б) (1 – 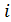 )(3 + 2
)(3 + 2 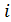 ) = 3 + 2
) = 3 + 2 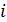 - 3
- 3 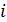 - 2
- 2 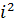 = 3 –
= 3 – 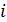 +2 = 5 –
+2 = 5 – 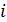 ;
;
в) 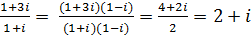 .
.
2. Выполнить действия:
а) 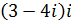 ; б)
; б) 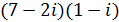 ; в)
; в) 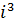 ; г)
; г) 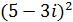 ; д)
; д) 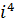 ; е)
; е) 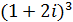 ;
;
ж) 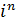 , где n – целое число.
, где n – целое число.
3. Вычислить:
а) 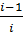 ; б)
; б) 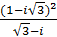 ; в)
; в) 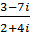 ; г)
; г) 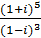 ; д)
; д) 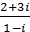 .
.
4. Заданы ли следующие комплексные числа в тригонометрической форме:
а) 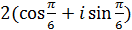 ; б)
; б) 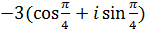 ; в)
; в) 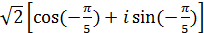 ;
;
г) 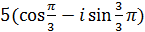 ; д)
; д) 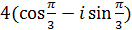 ; е)
; е) 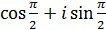 ;
;
ж) 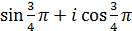 .
.
5. Записать в тригонометрической форме комплексные числа:
а) 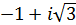 ; б)
; б) 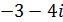 .
.
Решение.
а) 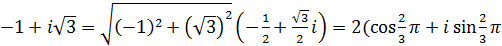 );
);
б) 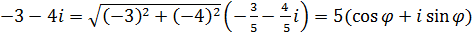 , где
, где 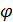 – угол третьей четверти, косинус которого равен
– угол третьей четверти, косинус которого равен 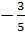 .
.
6. Представить в тригонометрической форме следующие комплексные числа:
а) 2; б) -5; в) 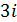 ; г)
; г) 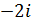 ; д)
; д) 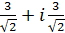 ; е)
; е) 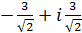 ; ж)
; ж) 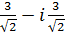 ; з)
; з) 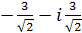 ;
;
и) 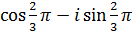 ; к)
; к) 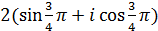 ; л)
; л) 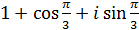 ; м)
; м) 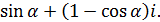
7. Вычислить, используя тригонометрическую форму комплексного числа:
а) 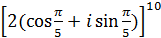 ; б)
; б) 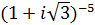 ;
;
Решение.
а) 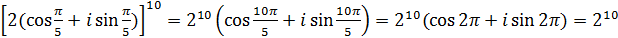 ;
;
б) 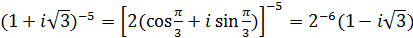 .
.
8. Вычислить, используя тригонометрическую форму комплексного числа:
а) 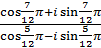 ; б)
; б) 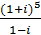 ; в)
; в) 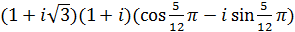 ;
;
г) 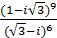 ; д)
; д) 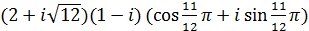 ;
;
е) 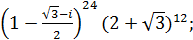 ж)
ж) 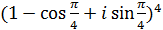 ; з)
; з) 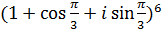 .
.
9. Найти все значения корней:
а) 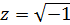 ; б)
; б) 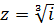 .
.
Решение.
а) 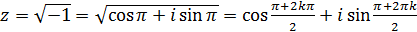 ;
;
k=0; 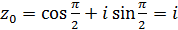 ;
;
k=1; 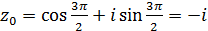 ;
;
б) 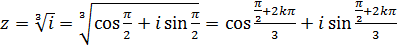 ;
;
k=0; 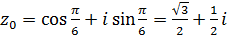 ;
;
k=1; 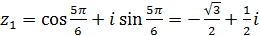 ;
;
k=2; 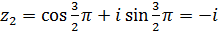 .
.
10. Найти все значения корней:
а) 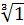 ; б)
; б) 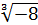 ; в)
; в) 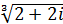 ; г)
; г) 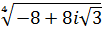 ; д)
; д) 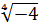 ; е)
; е) 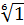 ;
;
11. Доказать, что:
а) 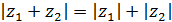 , если разность аргументов этих чисел равна
, если разность аргументов этих чисел равна 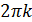 , k – целое число;
, k – целое число;
б) 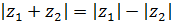 , если разность аргументов этих чисел равна
, если разность аргументов этих чисел равна 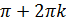 , k – целое число;
, k – целое число;
в) расстояние между точками 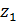 и
и 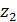 равно
равно 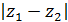 .
.
12. Построить на плоскости множество всех точек z, для которых:
а) 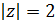 ; б)
; б) 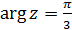 ; в)
; в) 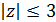 ; г)
; г) 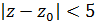 .
.
13. Решить уравнения:
а) 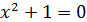 ; б)
; б) 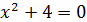 ; в)
; в) 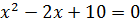 ; г)
; г) 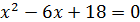 ;
;
д) 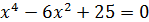 ; е)
; е) 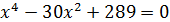 .
.
Процедура оценивания знаний, умений, навыков по дисциплине включает учет успешности выполнения практических работ, самостоятельной работы и тестовых заданий.
Практические работы считаются успешно выполненными в случае предоставления правильных ответов (решений) на вопросы (задачи) по теме работы. Шкала оценивания – «зачтено / не зачтено». «Зачтено» за практическую работу ставится в случае, если она полностью правильно выполнена, при этом обучающимся показано свободное владение материалом по дисциплине. «Не зачтено» ставится в случае, если работа решена неправильно, тогда она возвращается студенту на доработку и затем вновь сдается на проверку преподавателю.
Литература
Описание изданий основной литературы
1. Смирнова, Ю. М. Сборник задач по аналитической геометрии и линейной алгебре / Ю. М. Смирнова - Москва : Логос, 2017. - 376 с. - ISBN 5-94010-375-8. - Текст : электронный // ЭБС "Консультант студента" : [сайт]. - URL : https://www.studentlibrary.ru/book/ISBN5940103758.html
2. Ермаков, В.И. и др. Сборник задач по высшей математике для экономистов. М. ИНФРА-М. 2003. 575 с. 100экз.
3. Шерстов, С. В. Аналитическая геометрия и линейная алгебра: матрицы и системы уравнений / Шерстов С. В. - Москва : МИСиС, 2015. - 17 с. - ISBN 978-5-87623-970-9. - Текст : электронный // ЭБС "Консультант студента":[сайт].URL: https://www.studentlibrary.ru/book/ISBN9785876239709.html
4.Геворкян, П. С Высшая математика. Линейная алгебра и аналитическая геометрия / Геворкян П. С - Москва : ФИЗМАТЛИТ, 2014. - 208 с. - ISBN 978-5-9221-1582-7. - Текст : электронный // ЭБС "Консультант студента":[сайт].URL https://www.studentlibrary.ru/book/ISBN9785922115827.html
5. Беклемишев, Д. В. Решение задач из курса аналитической геометрии и линейной алгебры / Беклемишев Д. В. - Москва : ФИЗМАТЛИТ, 2014. - 192 с. - ISBN 978-5-9221-1480-6. - Текст : электронный // ЭБС "Консультант студента":[сайт].-URL : https://www.studentlibrary.ru/book/ISBN9785922114806.html
Описание изданий дополнительной литературы:
6. Ермаков, В.И. Общий курс высшей математики для экономистов. Учебник. - М.: ИНФРА-М, 2007. – 656 с. 70 экз.
7.Левин, В. А. Элементы линейной алгебры и аналитической геометрии на базе пакета "Mathematica". / Левин В. А. , Калинин В. В. , Рыбалка Е. В. - Москва : ФИЗМАТЛИТ, 2007. - 192 с. - ISBN 978-5-9221-0799-0. - Текст : электронный // ЭБС "Консультант студента" : [сайт]. - URL : https://www.studentlibrary.ru/book/ISBN9785922107990.html
Описание периодических изданий
8. Общероссийский портал Math-Net.Ru. Раздел "Журналы" — ключевой компонент портала — связывает российские периодические издания в области математических наук в единую информационную систему. http://www.mathnet.ru/ej.phtml?option_lang=rus
Перечень ресурсов информационно-телекоммуникационной сети "Интернет", необходимых для освоения дисциплины (модуля)
9. Нахождение определителя матрицы.
https://www.kontrolnaya-rabota.ru/s/matrix/determination/
10. Решение задач онлайн.
https://www.kontrolnaya-rabota.ru/s/
11. Решение системы уравнений в Microsoft Excel.
https://lumpics.ru/how-solve-system-equations-excel/#_4
12. Линии второго порядка на плоскости.
http://www.mathprofi.ru/linii_vtorogo_poryadka_ellips_i_okruzhnost.html
Интернет-ресурсы
13. Сайт Министерства финансов РФ www.minfin.ru
14. Сайт Министерства экономического развития РФ www.economy.gov.ru
15. МИР МАТЕМАТИЧЕСКИХ УРАВНЕНИЙ. Учебники и другие книги по математике. http://eqworld.ipmnet.ru/ru/library/mathematics.htm
16. Сайт Федеральной службы государственной статистики www.gks.ru
17.Научная электронная библиотека e-library.ru http://elibrary.ru
Источники ИОС
18. https://portal3.sstu.ru/Facult/SEI/BUH/
Профессиональные Базы Данных
19. Информационная справочная система «Гарант» https://www.garant.ru/








