10. Найти общее решение и одно частное решение системы уравнений
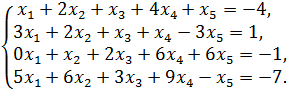
Решение. Запишем систему уравнений в виде таблицы:
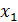
| 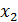
| 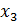
| 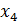
| 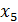
| b |
| 1 | 2 | 1 | 4 | 1 | -4 |
| 3 | 2 | 1 | 1 | -3 | 1 |
| 0 | 1 | 2 | 2 | 6 | -1 |
| 5 | 6 | 3 | 9 | -1 | -7 |
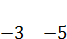
и найдем общее решение системы методом Гаусса.
Шаг 1. Данная система уравнений не содержит противоречивых и тривиальных уравнений. Первое уравнение не содержит разрешенного неизвестного.Неизвестное
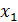 входит в это уравнение с коэффициентом единица. Исключив
входит в это уравнение с коэффициентом единица. Исключив 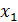 из других уравнений с помощью элементарных преобразований, получим систему уравнений
из других уравнений с помощью элементарных преобразований, получим систему уравнений
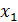
| 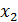
| 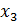
| 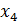
| 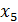
| b |
| 1 | 2 | 1 | 4 | 1 | -4 |
| 0 | -4 | -2 | -11 | -6 | 13 |
| 0 | 1 | 2 | 2 | 6 | -1 |
| 0 | -4 | -2 | -11 | -6 | 13 |
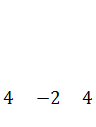
Шаг 2. Полученная после первого шага система не содержит противоречивых и тривиальных уравнений. Ни одно из уравнений, кроме первого, не содержит разрешенных неизвестных, но третье уравнение содержит неизвестное 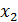 с коэффициентом единица. Исключим неизвестное
с коэффициентом единица. Исключим неизвестное 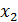 на остальных уравнений с помощью элементарных преобразований:
на остальных уравнений с помощью элементарных преобразований:
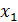
| 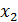
| 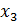
| 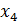
| 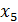
| b |
| 1 | 0 | -3 | 0 | -11 | -2 |
| 0 | 0 | 6 | -3 | 18 | 9 |
| 0 | 1 | 2 | 2 | 6 | -1 |
| 0 | 0 | 6 | -3 | 18 | 9 |
Шаг 3. Система уравнений, полученная после второго шага, не содержит противоречивых и тривиальных уравнении. Она не является разрешенной, так как второе уравнение не содержит разрешенного неизвестного. Разделим это уравнение на -3:
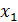
| 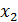
| 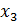
| 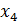
| 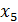
| b |
| 1 | 0 | -3 | 0 | -11 | -2 |
| 0 | 0 | -2 | 1 | -6 | -3 |
| 0 | 1 | 2 | 2 | 6 | -1 |
| 0 | 0 | 6 | -3 | 18 | 9 |
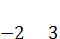
Теперь с помощью элементарных преобразований исключим неизвестное 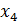 из третьего и четвертого уравнений:
из третьего и четвертого уравнений:
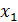
| 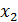
| 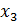
| 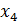
| 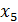
| b |
| 1 | 0 | -3 | 0 | -11 | -2 |
| 0 | 0 | -2 | 1 | -6 | -3 |
| 0 | 1 | 6 | 0 | 18 | 5 |
| 0 | 0 | 0 | 0 | 0 | 0 |
Итак, получена разрешенная система
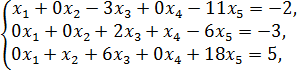
у которой 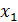 ,
, 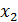 ,
, 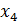 – разрешенные неизвестные, а
– разрешенные неизвестные, а 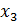 ,
, 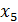 – свободные неизвестные. Общее решениеисходной системы имеет вид
– свободные неизвестные. Общее решениеисходной системы имеет вид
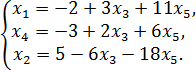
Если положить 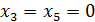 , то
, то 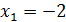 ,
, 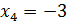 ,
, 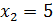 , т.е.
, т.е. 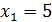 ,
, 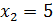 ,
, 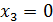 ,
, 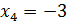 ,
, 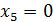 – частное решение исходной системы.
– частное решение исходной системы.
Исследовать совместность, найти общее решение и одно частное решение следующих систем уравнений:
11. 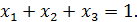
12. 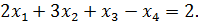
13. 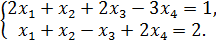
14. 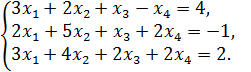
15. 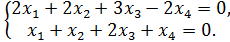
16. 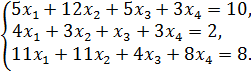
17. 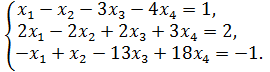
18. 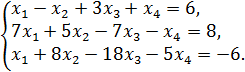
19. 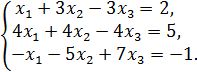
20. 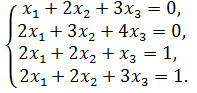
21. 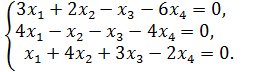
22. 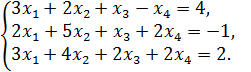
Тема 4. Линейные отображения.
Вопросы для обсуждения:
1. Понятие линейного отображения. Задание линейного отображения с помощью отображения базиса. Матрица линейного отображения. Связь между координатами вектора в различных базисах. Определения собственных векторов и собственных значений линейных операторов и методы их вычисления. Характеристическое уравнение.
2. Тематика рефератов:
1. Структура линейных операторов. Квадратичные формы.
2. Определение евклидова пространства. Критерий Сильвестра.
Задач и .
1.
Найти собственные значения матрицы
А= 
РЕШЕНИЕ. Найдём характеристической уравнение матрицы
Так как 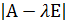 =
= 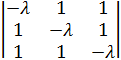 = -λ3+3λ +2,
= -λ3+3λ +2,
То
λ3+3λ +2=0  -(λ-2) (λ+1)2=0
-(λ-2) (λ+1)2=0
следовательно матрицы А имеет два собственных значения
λ 1=2 λ2=-1
2.
Найти собственные векторы матриц
А= 
Решение . в задаче 9.1 были найдены собственные значения матрицы А : λ 1=2 λ2=-1.
Теперь найдём множества А()2 и А(-1).система линейных уравнений (А-2Е) х = Ѳ, х =(х1,х2,х3),
Имеет вид
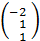 х1 +
х1 + 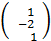 х2 +
х2 + 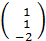 х3=
х3= 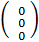
Её фундаментальная система решений состоит из одного вектора (1,1,1).следовательно вектор 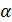 (1,1,1) –произвольный собственный вектор из А(2).
(1,1,1) –произвольный собственный вектор из А(2).
Теперь найдём множество А(-1). Векторы (-1,1,0) и (-1,1,0) образуют фундаментальную систему решений системы уравнений (А+Е)х=Ѳ и значит α (-1,1,0 )+ β(-1,0,1) – произвольный вектор из множества А(-1).
Найти собственные значения и собственные векторы матриц:
3 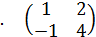 4.
4. 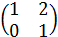
5. 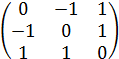 6.
6. 
7. 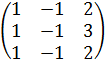 8.
8. 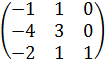 9.
9. 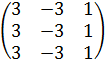 10.
10. 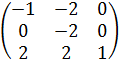
Тема 5. Аналитическая геометрия на плоскости: уравнение прямой
Вопросы для обсуждения:
1. Аналитическая геометрия на плоскости: уравнение прямой.
Задачи.
1. Построить прямые: а) Зх - y + 6 = 0; б) 5х +7у = 0; в) Зх – 4= 0; г) 5у + 4 = 0.
2. Определить параметры k и 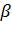 в уравнений (2.3) для каждой из прямых: а) 2х - 5у - 10. = 0; б) 2х + 5у = 0; в) у= 7; г)
в уравнений (2.3) для каждой из прямых: а) 2х - 5у - 10. = 0; б) 2х + 5у = 0; в) у= 7; г) 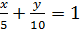
3. Уравнения прямых: а) Зх – 5y = 15; б) 5х - Зy + 10 = 0 привести к виду уравнения в отрезках на осях.
Решение. а) Данное уравнение нужно привести к виду 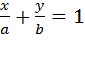 :
:
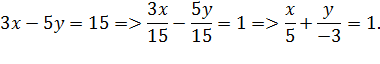
4. Дано общее уравнение прямой 12х - 5у - 65 .= 0. Написать,: а) уравнение с угловым коэффициентом; б) уравнение в отрезках на осях.
5. Можно ли уравнение прямой 19х + 98у = 0 записать в виде уравнения в отрезках на осях?
6. Какой угол образует с положительным направлением оси абсцисс прямая 5х + 5у - 7 = 0?
7. Определить площадь треугольника, образованного прямой 2х+ 5у - 20 = 0 с осями координат.
8. Написать уравнения сторон ромба с диагоналями 10 и 6 см, приняв большую диагональ за ось Ох и меньшую за ось Оу.
9. Написать уравнение прямой, проходящей через точку М(-4; 3) и отсекающей от координатного угла треугольник площадью, равной 3.
Указание. Использовать уравнение 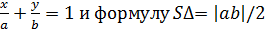
10. Даны точки O(0;0) и А(-3; 0). На отрезке OA построен параллелограмм, диагонали которого пересекаются в точке В(0; 2).Написать уравнения сторон и диагоналей параллелограмма.
11. Написать уравнение прямой, проходящей через точку М(4; 6) и отсекающей от осей 'Координат треугольник площадью, равной 6.
12. Составить уравнения прямых, проходящих через точку М(4;-5) и параллельных осям координат.








