1.2. Доказать: . Показать геометрически.

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

№1. Алгебра событий.

1.1. Получить результат геометрически: (A ◦ B) + (A ◦ C) + (B ◦ C).

1.2. Доказать: 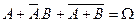. Показать геометрически.

1.3. Упростить ( А+В+С)(А+В)(А+В+ 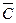)А.

1.4. Упростить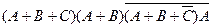

1.5. Упростить (А+В) ◦ (А+ 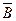)+(Ā+В) ◦ (Ā+ 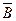). Проиллюстрировать геометрически.

1.6. Упростить (А+В) ◦ (Ā+ 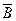)+(А+ 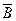) ◦ (Ā+В). Показать геометрически.

1.7. Проверить геометрически соотношение (А+В) ◦ С=АС + ВС.

1.8. Упростить (А+В)*(В+С). Показать геометрически.

1.9. Правильно ли соотношение ( А+В) ◦ С=Ā ◦ С+В ◦ С? Показать геометрически.

1.10. Правильно ли соотношение (А+В) ◦ С =Ā ◦ В ◦ С. Показать геометрически.

1.11. Упростить (A + B + C) – [(A ◦ B) + (A ◦ C) + (B ◦ C)]. Показать геометрически.

1.12. Показать геометрически результат: [C – (A + B)] + A◦B.

1.13. Найти геометрически результат: (A + B) – (A ◦ B + C).

1.14. Показать геометрически справедливость формул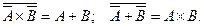

1.15. Доказать тождество (А+В) ◦ (А+В) ◦ (А+В) =А◦ В. Показать геометрически.

1.16. Доказать: А+Ā·В+А+В=Ω. Показать геометрически.

1.17. Получить результат геометрически: [(A ◦ B) + (A ◦ C) + (B ◦ C)] – ABC .

1.18. Обобщить формулы де Моргана: 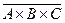=? Показать графически.

1.19. Получить результат геометрически: [C – (A + B)] + ABC .

1.20. Получить результат геометрически: [B + (A ◦ C)] – [(B ◦ C) + (A ◦ B)].

1.21. Получить результат геометрически: C + (A ◦ B) – [(A ◦ C) + (B ◦ C)].

1.22. Получить результат геометрически: A + B + C – [(A ◦ C) + (B ◦ C)].

1.23. Доказать, что Ā × В +А× В + А × В = А × В. Показать геометрически.

1.24. Доказать: 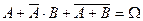. Показать графически.

1.25. Каково условие совместимости событий А+В, Ā+В, А+ 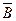. Показать графически.

1.26. Обобщить формулы де Моргана: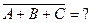

1.27. Обобщить формулы де Моргана: А+В+С=? Показать геометрически.

1.28. Обобщить формулы де Моргана: А◦В◦С=? Показать геометрически.

1.29. Упростить 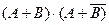. Показать геометрически.

1.30. Получить результат геометрически: (A – B) + (A ◦ C).

№2. Формулы комбинаторики.

2.1-2.5, 2.16-2.20. Сколькими различными способами можно расставить на полке собрание сочинений, состоящее из 10-ти томов, при условии, что первый и пятый тома не должны стоять рядом.

2.6-2.10, 2.21-2.25. Автокомбинат имеет 7 автомобилей малой грузоподъёмности и 10 большегрузных автомобилей. Нужно выбрать 3 автомобиля малой грузоподъёмности для обслуживания трёх торговых организаций и 5 большегрузных автомобилей для работы на стройке. Сколькими способами автокомбинат может осуществить свой выбор?

2.11-2.15, 2.26-2.30. Имеется пять кусков материи разных цветов. Сколько из этих кусков можно сшить различных флагов, если флаги состоят из трёх горизонтальных полос, причём две соседние полосы должны быть разного цвета?