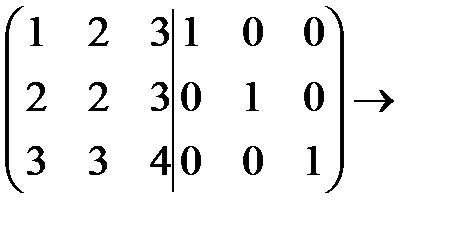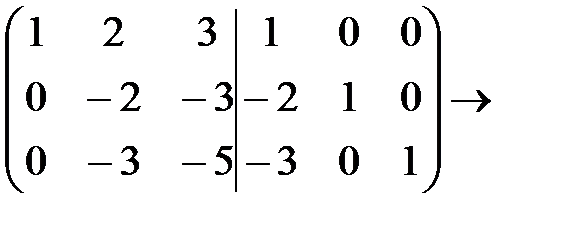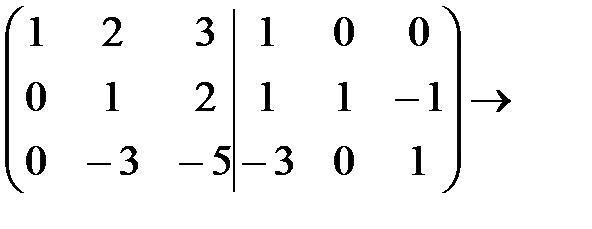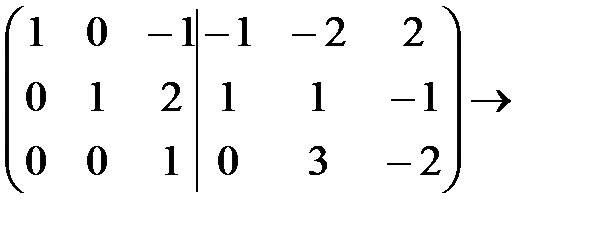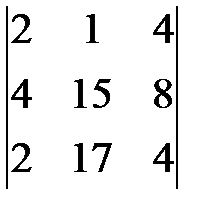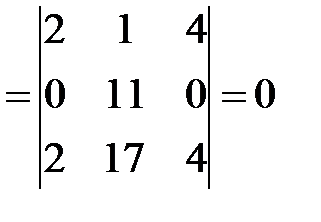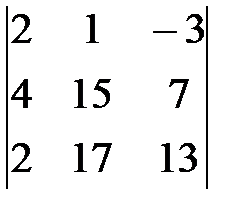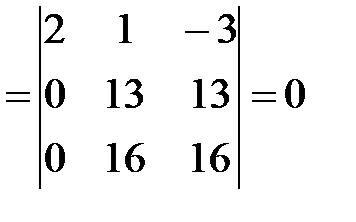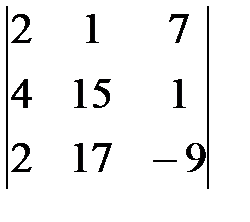Тема 2.2. Алгебра матриц. Обратные матрицы.
Вопросы для обсуждения:
Условие обратимости матрицы. Алгоритм нахождения обратной матрицы.
Тематика рефератов. Экономические примеры использования матриц :
1. Статическая модель межотраслевого баланса В. Леонтьева в матричной записи.
2. Продуктивность матрицы прямых затрат, критерии продуктивности.
Задачи.
1. Найти матрицу, обратную к матрице
А= 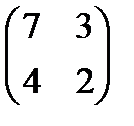 .
.
Р е ш е н и е. Определитель ∆ матрицы А равен 2, т.е. ∆ =2. Алгебраические дополнения её элементов : А11=2; А12= -4; А21= -3; А22=7. Следовательно,
А-1= 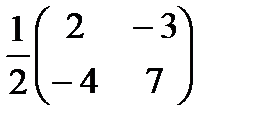 =
= 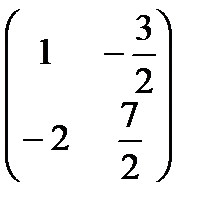 .
.
2. С помощью элементарных преобразований строк найти матрицу, обратную к матрице
А = 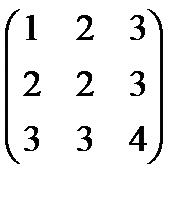 .
.
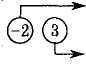
Р е ш е н и е. Припишем к матрице А справа единичную матрицу и будем выполнять элементарные преобразования строк объединенной матрицы до тех пор, пока матрица А не превратиться в единичную:

|
|
|
|
| |||||
|
|
|
|
| ||||
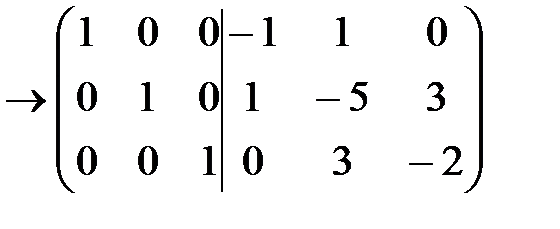 .
.
Таким образом,
А-1 = 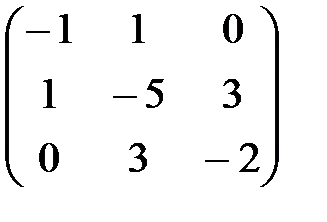 .
.
Найти обратную матрицу для следующих матриц:
2. 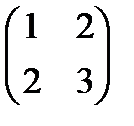 . 3.
. 3. 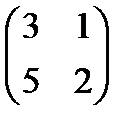 . 4.
. 4. 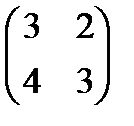 . 5.
. 5. 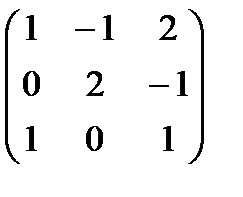 . 6.
. 6. 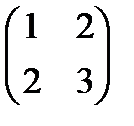 .
.
Тема 3.1. Системы линейных алгебраических уравнений. Метод Крамера.
Вопросы для обсуждения
1. Системы линейных уравнений (СЛУ). Формы записи систем линейных уравнений. Определения совместной, несовместной, определенной и неопределенной системы m линейных уравнений с n неизвестными. Нахождение решения системы линейных алгебраических уравнений по формулам Крамера
Задачи.
1. Решить систему уравнений
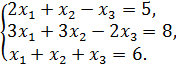
Решение. Вычислим определитель матрицы системы уравнений:
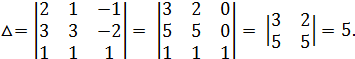
Следовательно, система имеет единственное решение, которое можно найти с помощью формул Крамера.
Вычислим определители:
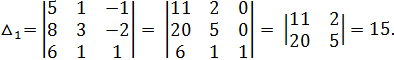
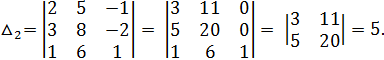
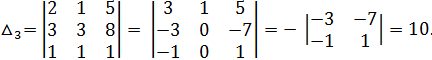
По формулам Крамера находим:
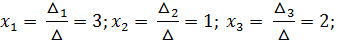
Решить системы уравнений:
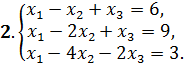
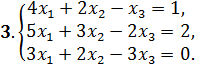
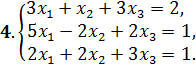
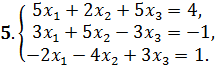
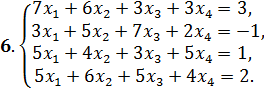
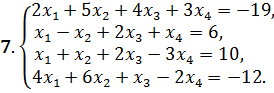
Тема 3.2. Системы линейных алгебраических уравнений.
Метод Жордано-Гаусса.
Вопросы для обсуждения:
Определение арифметического n-мерного векторного пространства. Метод Жордано-Гаусса. Теорема Кронекера-Капелли и следствие из нее. Вычисление ранга матрицы. Теорема о решении однородной СЛУ и следствие из нее. Нахождение решения системы линейных алгебраических уравнений матричным методом.
Задач и
1. Вычислить методом окаймления миноров ранг матрицы:
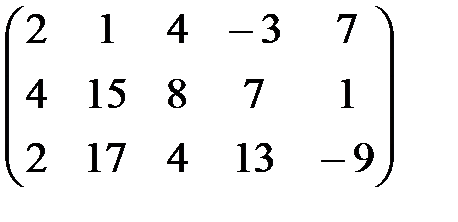
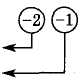
Р е ш е н и е. Так как матрица содержит ненулевые элементы, то ее ранг не меньше 1. Минор второго порядка d = 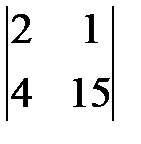 отличен от нуля и, значит, ранг матрицы не меньше 2. Вычислим окаймляющие d миноры третьего порядка:
отличен от нуля и, значит, ранг матрицы не меньше 2. Вычислим окаймляющие d миноры третьего порядка:
|
|
|
| |||||
|
|
|
| |||||
|
|
| 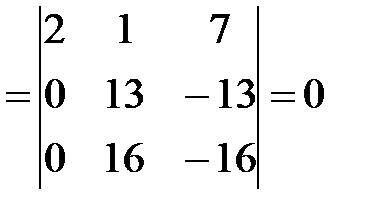
| |||||
Итак, все миноры, окаймляющие минор d, равны нулю. Следовательно, ранг данной матрицы равен 2.
2. Найти с помощью элементарных преобразований ранг матрицы:
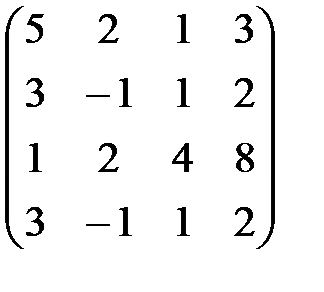 .
.
Р е ш е н и е. Превратим данную матрицу в трапецеидальную с помощью элементарных преобразований:
|
|
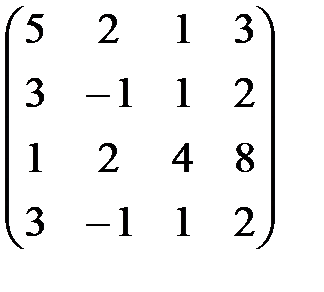
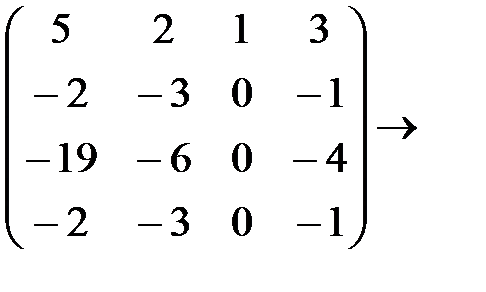
|
|
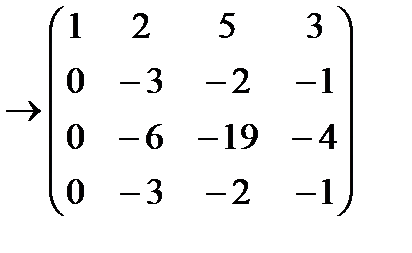
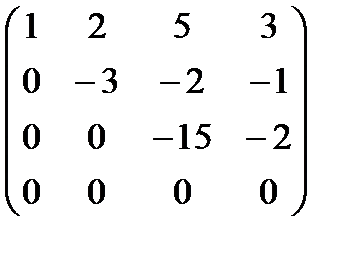
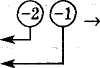
Таким образом, ранг матрицы равен 3.
Найти ранг матрицы:
3. 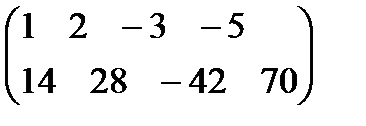 . 4.
. 4. 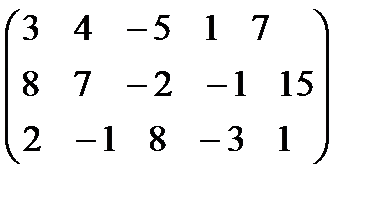 .
.
5. 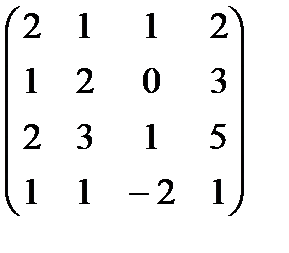 . 6.
. 6. 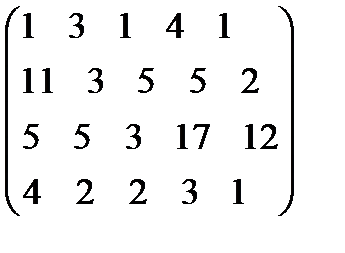 .
.
7. 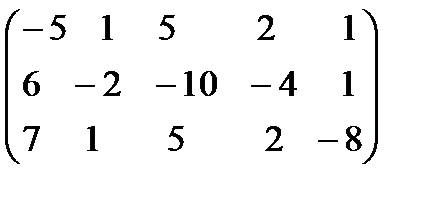 . 8.
. 8. 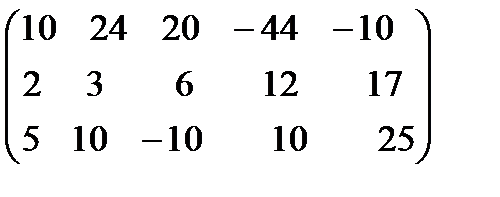 .
.
9. Исследовать совместимость, найти общее решение и одно частное решение системы уравнений
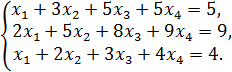
Решение 1. Выпишем расширенную матрицу, найдем ее ранг и одновременно ранг матрицы системы уравнений:
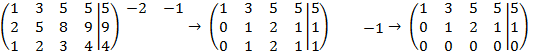
Итак, ранги матрицы и расширенной матрицы совпадают и равны 2. Следовательно, система совместна.
2. Выберем минор М = 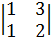 , составленный из коэффициентов при неизвестных
, составленный из коэффициентов при неизвестных 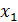 и
и 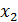 первого и третьего уравнений. Этот минор отличен от нуля и его порядок равен рангу матрицы системы.
первого и третьего уравнений. Этот минор отличен от нуля и его порядок равен рангу матрицы системы.
3. Выипишем первое и третье уравнение данной системы , которые содержат строки минора М:
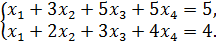
В этих уравнениях оставим в левой части неизвестные 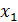 и
и 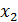 , коэффициенты при которых являются столбцами минора М, а остальные неизвестные перенесем в правую часть:
, коэффициенты при которых являются столбцами минора М, а остальные неизвестные перенесем в правую часть:
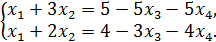
4. Решим полученную систему по формуле Крамера:
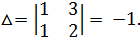
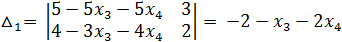
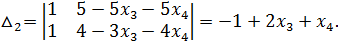
Теперь имеем
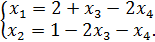 – общее решение данной системы.
– общее решение данной системы.
Неизвестные 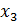 и
и 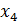 – свободные неизвестные. Если положить
– свободные неизвестные. Если положить 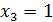 ,
, 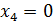 , из общего решения находим
, из общего решения находим 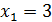 ,
, 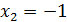 . Следовательно,
. Следовательно, 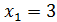 ,
, 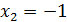 ,
, 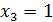 ,
, 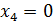 – частное решение исходной системы уравнений.
– частное решение исходной системы уравнений.