Тема 1. Определитель и его свойства. Линейные векторные пространства.
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Саратовский государственный технический университет имени Гагарина Ю.А.»
Кафедра «Информационные системы и моделирование»
Методические указания
для проведения самостоятельных практических занятий
для студентов
по дисциплине «Линейная алгебра»
Утверждено на заседании УМКН
«___»___________2021 года, протокол № ___
Председатель УМКН ____________/ Лобачева Г.В.
Саратов 2020
ОБЩИЕ ПОЛОЖЕНИЯ
Целями освоения дисциплины «Линейная алгебра» являются формирование умения использовать законы естественнонаучных дисциплин в профессиональной деятельности, формирование у студентов понимания роли математики в современном мире, знакомство студентов с основными понятиями и методами линейной алгебры, формирование у студентов системного математического мышления, умения применять математический аппарат для исследования экономических процессов.
Задачи изучения дисциплины:
1. приобретение и развитие навыков математического мышления и в применении к решению задач линейной алгебры и осознание ее роли в развитии других наук;
2. овладение основными понятиями и методами линейной алгебры; навыками использования алгебраического аппарата для решения теоретических и прикладных задач в математике, информатике и экономике для моделирования и теоретического исследования;
3. формирование:
– готовности использовать алгебраический аппарат для решения теоретических и прикладных задач в математике, информатике и экономике;
– выработке умений анализировать полученные результаты;
– мотивации и способностей для самостоятельного повышения уровня своего научного мировоззрения
Важным элементом образовательного процесса является проведение практических занятий, ориентированных на выработку у студентов практических навыков и умений, которые в дальнейшем пригодятся в их профессиональной деятельности. Настоящие методические указания содержат материал, пригодный для использования преподавателями на практических занятиях по дисциплине «Линейная алгебра».
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
Тема 1. Определитель и его свойства. Линейные векторные пространства.
Вопросы для обсуждения:
Перестановки и инверсии. Квадратные матрицы и определители. Определитель 3 порядка, вычисление с помощью правил треугольника, Саррюса. Свойства определителей. Минор, дополнительный минор и алгебраическое дополнение. Теорема Лапласа и следствия. Разложение определителя по строке (столбцу). Приведение определителя к треугольному виду.
Вектор, основные операции над векторами. Определение векторного пространства. Линейная зависимость векторов и базис конечномерного векторного пространства. Связь между различными базисами векторного пространства. Связь между координатами векторов в различных базисах.
Тематика рефератов:
1. Связь между различными базисами векторного пространства.
2. Связь между координатами векторов в различных базисах.
Задач и.
1 .
Выполнить следующие действия:
2* 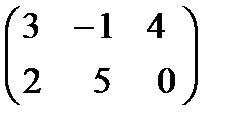 - 3*
- 3* 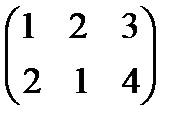 .
.
Решение.
2* 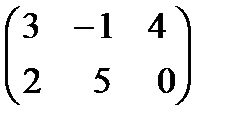 - 3*
- 3* 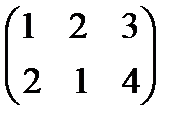 =
= 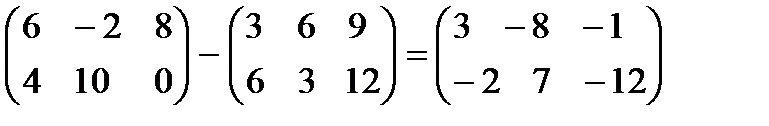 .
.
2. Вычислить определитель матрицы

Решение. Использую приведенные выше схемы, получаем
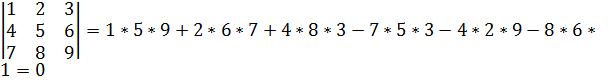 .
.
3. Вычислить определитель, разлагая его по элементам третьего столбца:
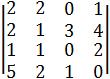
Решение.
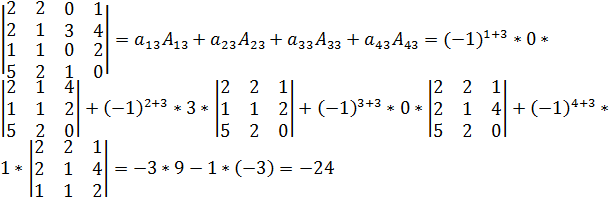 .
.
4. Вычислить определитель матрицы путем разложения его по элементам второй строки:
а) 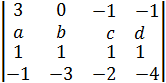 ; б)
; б) 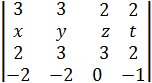 .
.
5. Вычислить определитель матриц, разлагая их по строке или столбцу:
а)  ; б)
; б) 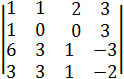 ; в)
; в) 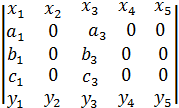 ;
;
г) 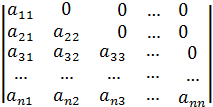 ; д)
; д) 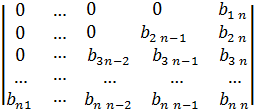 ;
;
Тема 2 . 1. Алгебра матриц. Произведение матриц.
Вопросы для обсуждения
Прямоугольные матрицы. Операции над ними: сумма, разность, произведение, умножение на скаляр. Произведение матриц. Присоединенная и обратная матрицы.
Задачи.
1. Найти элемент с32 матицы АВ=(с ij ), если
А= 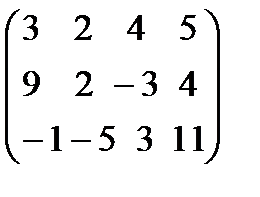 ; В=
; В= 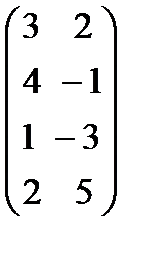 .
.
Р е ш е н и е. Элемент с32 равен сумме произведений элементов третьей строки матрицы А на соответствующие элементы второго столбца матрицы В, т.е.
С32=(-1) * 2+ (-5)*(-1)+3*(-3)+11*5=49.
2. Вычислить произведение матриц
А= 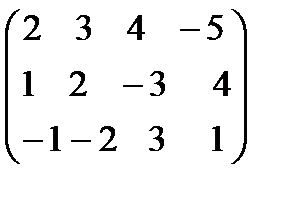 ; В=
; В= 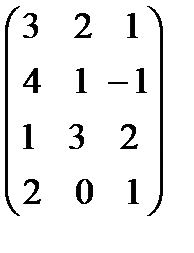 .
.
Р е ш е н и е. Так как сомножители имеют размеры 3X4 и 4 X3, то их произведение определен и имеет размеры 3X3. Следовательно,
АВ= 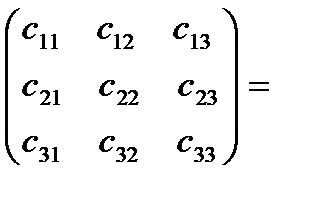
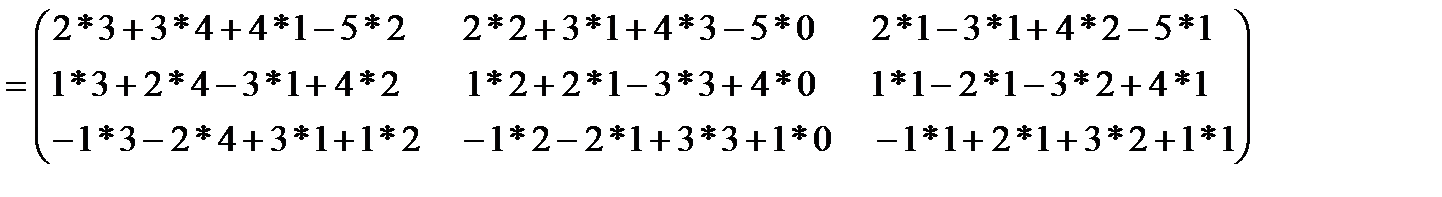 =
=
= 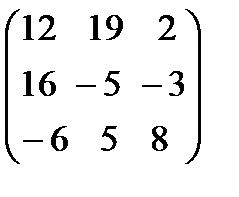 .
.
Для закрепления темы необходимо решить задачи.
Найти произведение матриц.
3. 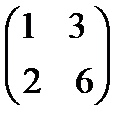
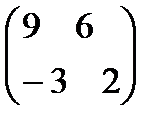 . 4.
. 4. 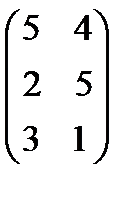
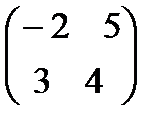 .
.
5. 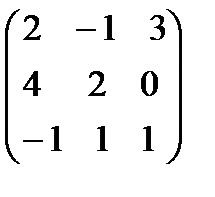
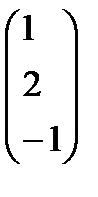 . 6.
. 6. 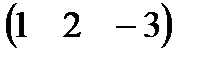
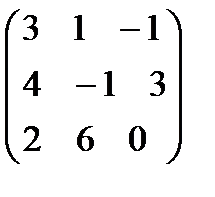 .
.
7. (1 -1 3)  . 8.
. 8. 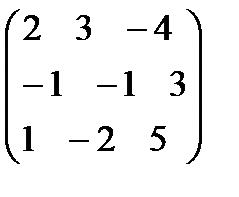
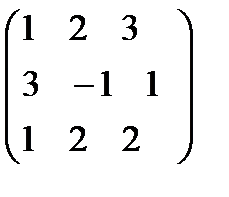 .
.
9. Найти матрицу, обратную к матрице
А= 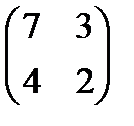 .
.
Р е ш е н и е. Определитель ∆ матрицы А равен 2, т.е. ∆ =2. Алгебраические дополнения её элементов : А11=2; А12= -4; А21= -3; А22=7. Следовательно,
А-1= 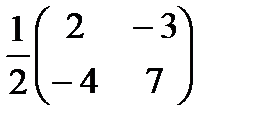 =
= 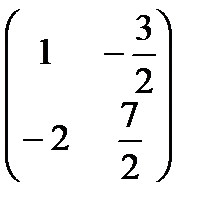 .
.
Найти обратную матрицу для следующих матриц:
10. 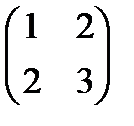 . 11.
. 11. 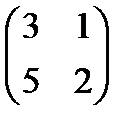 . 12.
. 12. 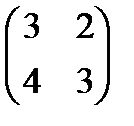 . 13.
. 13. 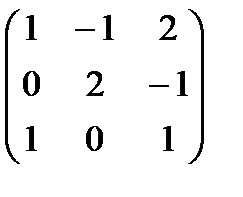 .
.








