Повторение материала прошлых уроков
Графики зависимости кинематических величин от времени при равноускоренном движении.
Цели урока:
- повторить уравнения движения;
- научиться строить, читать, понимать графики зависимости кинематических величин от времени
- на наглядном примере изучить равномерное прямолинейное движение с помощью графиков зависимости.
Повторение материала прошлых уроков
Начнем с повторения основных понятий и терминов, связанных с движением. Прочтите и постарайтесь дать устные ответы ( назвать величину по ее характеристике):
1. Физическая величина, длина траектории.
2. Физическая величина, характеризующая быстроту изменения координаты тела.
3. Направленный отрезок (вектор), соединяющий начальное и конечное положение тела.
4. Физическая величина, характеризующая быстроту изменения скорости.
5. Изменение положения тела в пространстве относительно других тел с течением времени.
6. Линия, по которой движется тело.
Посмотрите ответы:
1. Путь
2. Скорость
3. Перемещение
4. Ускорение
5. Механическое движение
6. Траектория
Теперь давайте вспомним формулы, необходимые нам на уроке.
Прочтите и постарайтесь дать устные ответы (вспомнить формулу по ее характеристике):
1. Формулу пути (проекции перемещения) при равномерном движении
2. Формулу нахождения координаты при равномерном движении
3. Формулу проекции ускорения при равноускоренном движении
4. Формулу проекции скорости при равноускоренном движении
Посмотрите ответы:
1. s = vt
2. x = xo + vt
3. a = (v – vo ) / t
4. v = vo + at
Рассмотрим задачу. (Разберите решенную задачу на движение)
Задача1. По графику зависимости координаты тела от времени постойте график его скорости.
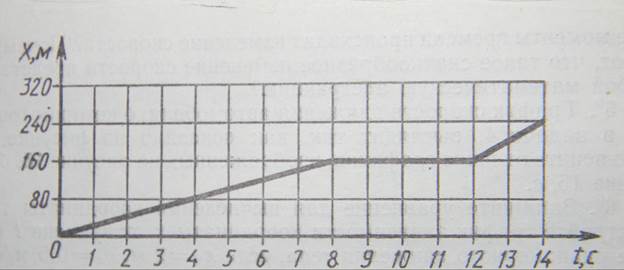
Для этого определим скорость на различных участках. О движении какого тела может идти речь в этой задачи? В какие моменты времени происходит изменение скорости? Почему считают, что такое скачкообразное изменение скорости представляет собой математическую абстракцию? Давайте внесем изменения в график.
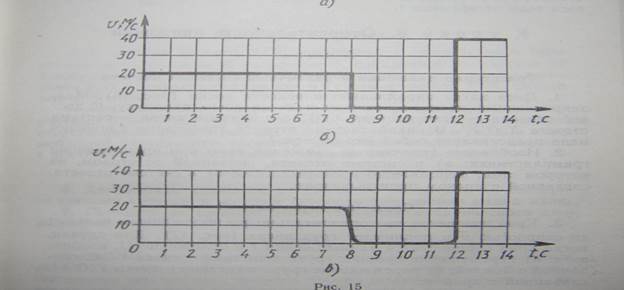
О движениях сложено много пословиц и поговорок:
· тише едешь - дальше будешь
· крутится, как белка в колесе
· язык до Киева доведет
· за двумя зайцами погонишься – ни одного не поймаешь
· плывет по течению
· умный в гору не пойдет, умный гору обойдет
Если скорость тела меняется, значит, движение становится неравномерным и появляется ускорение, характеризующее быстроту изменения скорости.
Перейдем к рассмотрению новой темы.
Самое простое из всех неравномерных движений — это прямолинейное движение с постоянным ускорением.
При движении с постоянным ускорением (a→=const−→−−) скорость тела линейно зависит от времени:
v→=v→o+a→t.
В проекциях на ось Ox данные равенства имеют вид:
ax=const;
vx=vox+axt.
Построим графики зависимостей ax(t) и vx(t) для случаев ax>0 и ax<0.
Примем vox>0.
Поскольку в обоих случаях ax=const, то графиком зависимости ax(t) ускорения от времени в обоих случаях будет прямая, параллельная оси времени.
Только при ax>0 данная прямая будет лежать в верхней полуплоскости (рис. 1), а при ax<0 — в нижней (рис. 2).
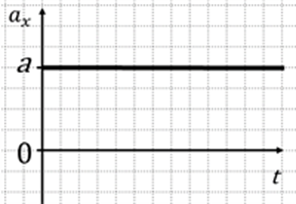
Рис. 1
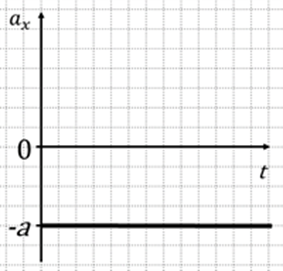
Рис. 2
Графиком зависимости скорости движения тела от времени vx(t) является прямая, пересекающая ось скорости в точке v0 и образующая с положительным направлением оси времени острый угол при ax>0 (рис. 3) и тупой угол при ax<0 (рис. 4).
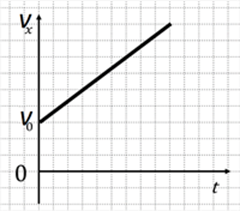
Рис. 3
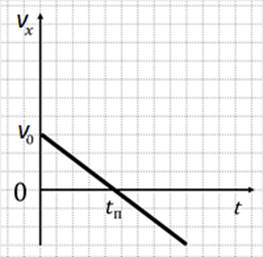
Рис. 4
График на рисунке 3 описывает возрастание проекции скорости vx. При этом модуль скорости тела также растёт. Данный график соответствует равноускоренному движению тела.
График на рисунке 4 показывает, что проекция vx скорости тела вначале положительна.
Она уменьшается и в момент времени t=tп становится равной нулю.
В этот момент тело достигает точки поворота, в которой направление скорости тела меняется на противоположное, и при t>tп проекция скорости становится отрицательной.
Из последнего графика также видно, что до момента поворота модуль скорости уменьшался — тело двигалось равнозамедленно.
При t>tп модуль скорости растёт — тело движется равноускоренно.
Для любого равнопеременного прямолинейного движения площадь фигуры между графиком vx и осью времени t численно равна проекции перемещения Δrx.
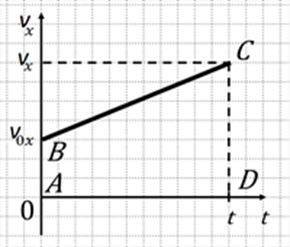
Рис. 5
Согласно данному правилу, проекция перемещения Δrx при равнопеременном движении определяется площадью трапеции ABCD (рис. 5). Эта площадь равна полусумме оснований трапеции, умноженной на её высоту:
S=AB+DC2⋅AD.
В результате:
Δrx=vox+vx2⋅Δt.
Из данной формулы получим формулу для среднего значения проекции скорости:
vxср=ΔrxΔt=vox+vx2.
При движении с постоянным ускорением данное отношение выполняется не только для проекций, но и для векторов скорости:
vcp−→=vo→+v→2.








