Расчет величины момента инерции маховика

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Приведенный момент инерции механизма можно представить в следующем виде:

При ω=ω _max I _пр. ^max = I _{пост.часть} + I _махов. + Δ I ^max , (4.21)

при ω=ω _min I _пр. ^min = I _{пост.часть} + I _махов. + Δ I ^min , (4.22)

где I _{пост.часть} – постоянная составляющая приведенного момента инерции механизма,

I _махов. – момент инерции маховика или маховых масс (в т.ч. колес, валов и т.д.) (величина постоянная для данного механизма);

Δ I ^max - составляющая приведенного момента инерции при максимальной скорости в цикле ω _max.;

Δ I ^min – составляющая приведенного момента инерции при минимальной скорости в цикле ω _{min .}.

Тогда

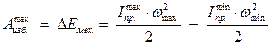(4.23)

Из (4.23) следует (если , )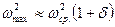

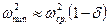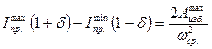(4.24)

С учетом (4.19) и (4.20) получим:

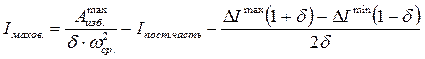(4.25)

Для определения величины I _махов. задаются величинами ω_ср. и δ.

Формулу (4.25) можно упростить, если принять, что Δ I_max = Δ I_min. Тогда

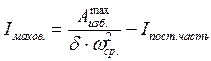(4.26)

При больших маховых массах (когда I _махов. >> I _{пост.часть}) можно приближенно принять:

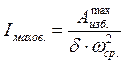(4.27)

Для определения величины 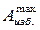можно пользоваться диаграммами моментов сил движущих М_дв.( φ ) и сил сопротивлений М_сопр.( φ ) (рис. 4.10)

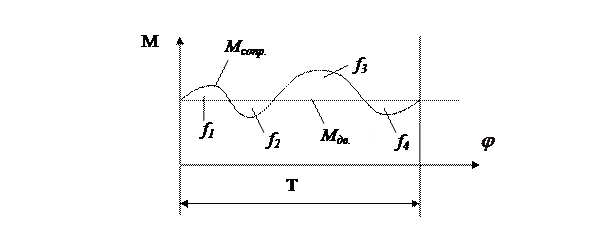
Рис. 4.10 Моменты сил движущих и сил сопротивлений в цикле Т

Площади f ₁…f ₄, ограниченные кривой М_сопр. и графиком М_дв., представляют собой разности работ движущих моментов М_дв. и моментов сопротивлений М_сопр.. Причем суммы площадей имеют соотношение

f₁ + f₃ = f₂ + f₄.

Выбирают наибольшую из заштрихованных площадей. Если 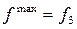, то величину максимальной избыточной работы можно определить по формуле

,

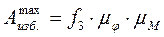где μ_φ и μ_М – масштабы графиков по ося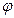м и М.

Регулирование непериодических колебаний угловой скорости главного вала машины производится с помощью специальных регуляторов. Одним из простейших является центробежный регулятор (регулятор Дж. Уатта).