Определение КПД машинного агрегата при последовательном соединении входящих в него механизмов
Рассмотрим машинный агрегат, состоящий из последовательно соединенных механизмов, условно обозначенных на схеме (рис. 4.6) цифрами 1, 2 и 3.
|
|
|
|
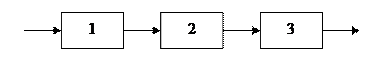
Рис. 4.6. Машинный агрегат с последовательно соединенными механизмами
Пусть к механизму 1 подводится работа величиной А. На выходе мы получаем работу величиной А1, которая подводится к механизму 2 и т. д. Причем величина работы на выходе всегда меньше, чем подведенная работа на входе (А1<A, A2<A1, A3<A2), так как в каждом механизме имеются механические потери подведенной к нему работы.
Тогда общий КПД машинного агрегата равен:
.
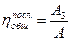а КПД каждого механизма можно выразить так:
; 
; 
.
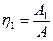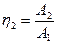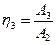Перемножим КПД всех последовательно соединенных механизмов и получим:
.
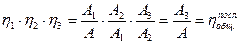Отсюда следует обобщенный вывод: общий механический КПД машинного агрегата, состоящего из последовательно соединенных n механизмов, равен произведению их КПД:
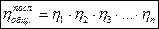(4.17)
Определение КПД машинного агрегата при параллельном соединении входящих в него механизмов
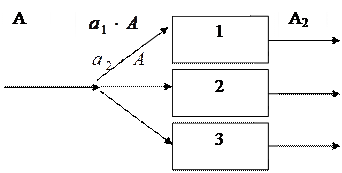
Рассмотри машинный агрегат, состоящий из трех параллельно соединенных механизмов, условно обозначенных на схеме (рис. 4.7) цифрами 1,2 и 3. Пусть к механизмам подводится работа величиной А, которая распределяется на каждый механизм в разных долях, определяемых коэффициентами а1, а2, а3, каждый из которых меньше 1, а их сумма равна
а1 + а2 + а3 = 1
 |
 |
Рис. 4.7 Машинный агрегат с параллельно соединенными механизмами
Тогда общий КПД всего машинного агрегата можно выразить отношением суммы работ на выходе механизмов к общей подведенной работе А:
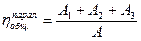(4.18)
Так как
; 
,
; 
,
; 
,
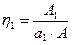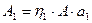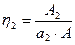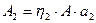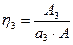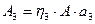то, подставив эти выражения в (4.18), получаем
.
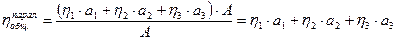Отсюда следует, что общий механический КПД машинного агрегата при параллельном соединении механизмов равен сумме величин КПД каждого механизма, умноженных на коэффициенты долей работ, подводимых к механизмам:
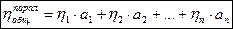(4.18)
Сравним варианты последовательного и параллельного соединения механизмов с точки зрения минимизации механических потерь в машинном агрегате.
Пусть величины КПД каждого механизма равны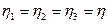 
. При этом коэффициенты, учитывающие доли распределения общей работы А между всеми механизмами, также равны
.
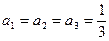Тогда
, 
.
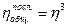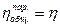Так как η < 1, то η3 < η. Отсюда следует, что параллельное соединение механизмов в машинном агрегате предпочтительнее с точки зрения уменьшения механических потерь.
Самоторможение.
Если Адв.<Авред.сопрот., то действительного движения механизма произойти не может. Это называется явлением самоторможения. Следовательно, если при теоретических расчетах получим η < 0, то это значит, что механизм в заданном направлении двигаться не может.
Для возможности движения механизма необходимо обеспечить условие:
0 ≤ η < 1.
4.7. Неравномерность хода ведущего звена машины
Уравнение движения главного вала машины в форме кинетической энергии имеет вид (см. формулу 4.12):
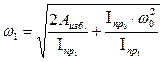
Так как величина избыточной работы Аизб., являясь функцией угла поворота вала φ, угловой скорости ω и времени t, есть величина переменная, т.е. Аизб. = f ( φ, ω, t ), при этом I пр = f (φ ), то при установившемся режиме работы машины угловые скорости в начале и конце одного цикла Т (например, одного оборота) равны: ω0нач.= ω0кон.= ωср (рис. 4.8)
При этом за цикл изменение кинетической энергии равно нулю ΔЕ = 0. Внутри цикла угловая скорость вала может меняться. Это вызывает дополнительные динамические (инерционные) нагрузки, а также дополнительное трение в кинематических парах, что снижает надежность механизма и его КПД.
При этом ухудшаются условия работы механизма, приходится увеличивать материалоемкость машины, повышая прочность звеньев, нести дополнительные энергетические затраты на преодоление трения.
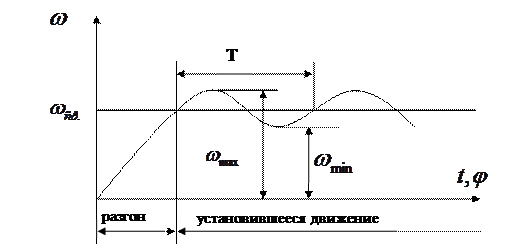
Рис. 4.8. Периодические колебания угловой скорости главного вала машины в период установившегося движения
Коэффициент неравномерности хода ведущего вала машины δ выразим формулой
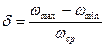, (4.19)
где
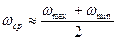(4.20)
Из (4.19) и (4.20) получим:
ωmax = ωcp (1 +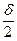 
); ωmax2 ≈ ωср2 (1 + δ);
ωmin = ωcp (1 - 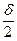); ωmin2 ≈ ωср (1 - δ).
Величина δ может находиться в следующих пределах: для ударных машин, прессов δ≤ 
, для металлорежущих станков δ=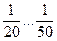 
, для двигателей δ≤ 
.
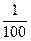4.8. Регулирование периодических колебаний угловой скорости с помощью маховика
В случае необеспечения требуемой величины δ при работе машины могут возникнуть нежелательные явления и процессы (вибрация, повышенные энергетические затраты, невозможность выполнения технологического процесса и т.д.). При условии периодических колебаний угловой скорости вала для получения заданной величины δ используют маховик – массивное колесо с большим моментом инерции.
Основная задача при расчете маховика – это определение его момента инерции. Маховик с таким моментом инерции I махов. в интервале скоростей от ω max до ω min (рис. 4.5) должен произвести работу, равную изменению кинетической энергии механизма за это время:
Аизб. max = Δ E ме x .