Уравнение (4.12) называют уравнением движения машины в форме кинетической энергии.
4.4. Уравнение движения машины в дифференциальной форме
Уравнение (4.11) можно записать в следующем виде:
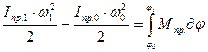 , (4.13)
, (4.13)
где Мпр.=Мпр.дв.+Мпр.сопр. – суммарный приведенный момент сил движущих и сил сопротивлений.
Продифференцируем (4.13) по переменной φ:
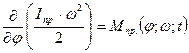 ;
;
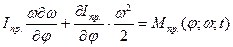 (4.14)
(4.14)
Преобразуем 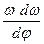 , разделив числитель и знаменатель на
, разделив числитель и знаменатель на 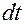 , и получим:
, и получим:
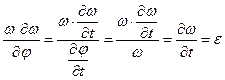 ,
,
где 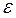 - угловое ускорение.
- угловое ускорение.
Тогда уравнение (4.14) можно записать в следующем виде:
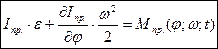 (4.15)
(4.15)
Это есть дифференциальное уравнение движения машины для ведущего вращающегося ведущего звена.
Дифференциальное уравнение движения машины для поступательно движущегося ведущего звена выводится аналогично предыдущим выкладкам и имеет вид:
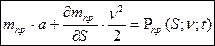 (4.16)
(4.16)
Решать дифференциальные уравнения движения можно графическим или численным методом (методом последовательных приближений).
4.4 Режимы движения машины
В общем виде движения машины можно разделить на три основных режима (периода): разгон, установившееся движение и останов (рис. 4.5).
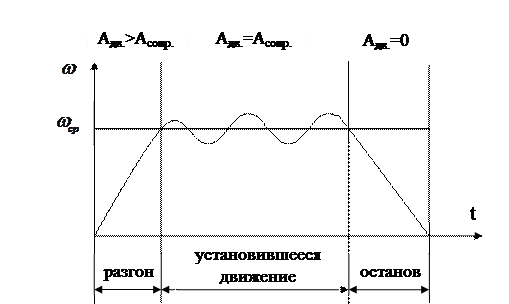
Рис. 4.5. Схема режимов движения машины
В режиме разгона угловая скорость в начале режима 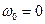 , в конце
, в конце 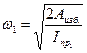 , что следует из уравнения (4.12). При этом всегда
, что следует из уравнения (4.12). При этом всегда 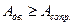 , иначе разгон невозможен.
, иначе разгон невозможен.
В режиме установившегося движения 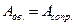 , изменение кинетической энергии (в среднем за один оборот ведущего вала)
, изменение кинетической энергии (в среднем за один оборот ведущего вала) 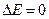 . В пределах одного оборота происходят периодические колебания угловой скорости вала машины.
. В пределах одного оборота происходят периодические колебания угловой скорости вала машины.
В режиме останова (когда двигатель отключен) 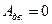 . При этом выполняется работа, затрачиваемая на преодоление сил трения
. При этом выполняется работа, затрачиваемая на преодоление сил трения 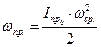 .
.
4.5. Механический КПД механизма
В период установившегося движения машины соблюдается условие равенства работ сил движущих и сил сопротивлений:
Адв.=Асопр.
Работа сил сопротивления складывается из суммы работ сил полезного сопротивления Апол.сопр. и сил вредного сопротивления Авр.сопр.. Тогда
Адв. = Апол.сопр. + Авр.сопр.
Разделим левую и правую части равенства на величину работы сил движущих:
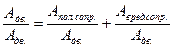
и получим
1 = η + φ , где
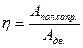 - механический (цикловой) коэффициент полезного действия (КПД),
- механический (цикловой) коэффициент полезного действия (КПД),
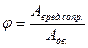 - коэффициент механических потерь.
- коэффициент механических потерь.








