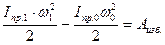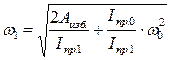Приведенная масса механизма

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Заменим условно механизм его динамической моделью. Например, кривошипно – ползунный механизм (рис.4.2) заменим динамической моделью, состоящей из стойки и кривошипа.

 

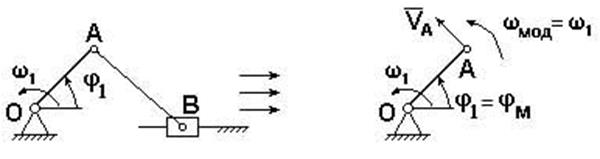Рис. 4.2. Замена кривошипно – ползунного механизма динамической моделью

 

Здесь ОА – звено приведения механизма, в котором как бы сосредоточена инертность всех звеньев механизма, А – точка приведения.

Уравнение (4.2) умножим и разделим на квадрат скорости точки приведения VA

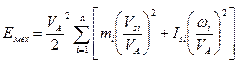(4.3)

В этом уравнении выражение в квадратных скобках имеет размерность массы (кг). Его называют приведенной массой m пр. механизма в точке А.

Тогда 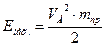, где

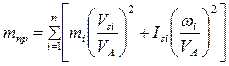(4.4)

Приведенной массой механизма называется такая условная масса, которая как бы сосредоточена в точке приведения механизма, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.

 

Приведенный момент инерции

Так как 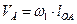, где 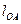– длина звена приведения, 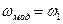– его угловая скорость, то кинетическую энергию механизма можно выразить следующим уравнением:

 

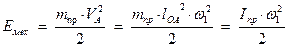, (4.5)

 

где 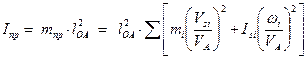(4.6)

– приведенный момент инерции механизма.

Приведенным моментом инерции механизма называется такой условный момент инерции, которым как бы обладает звено приведения относительно оси вращения, кинетическая энергия которого (при таком моменте инерции) равна сумме кинетических энергий всех звеньев механизма.

Величины m пр. и J пр. не являются постоянными для данного механизма, а меняют свое численное значение в зависимости от положений звеньев, так как звенья меняют свои скорости.

Пример: Определить приведенную массу и приведенный момент инерции для заданного положения кривошипно – ползунного механизма (рис. 4.3), если известны положения центров масс звеньев (S 1 и S 2), линейные и угловые скорости звеньев и центров масс звеньев: 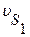, 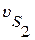и 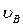- скорости центров масс кривошипа, шатуна и ползуна, 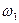и 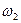- угловые скорости кривошипа и шатуна.

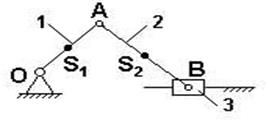
Рис. 4.3. Кривошипно – ползунный механизм.

 

Пусть кривошип 1 – звено приведения, А – точка приведения.

Приведенная масса механизма согласно (4.4) вычисляется по формуле

,

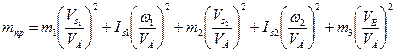приведенный момент инерции согласно (4.6)

 

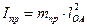
4.3. Уравнение движения машины в форме кинетической энергии

Рассмотрим состояние механизма при двух различных положениях ведущего звена, разделяемых каким – либо промежутком времени dt или, например, углом d φ поворота ведущего звена - кривошипа (рис. 4.4).

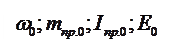
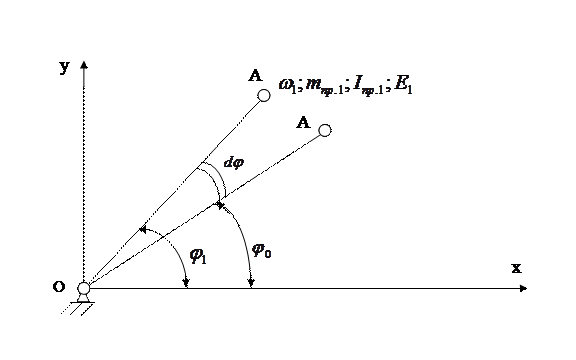
Рис. 4.4. Кинематические и динамические параметры механизма при различных положениях звена приведения.

 

При положении кривошипа φ0 угловая скорость звена приведения ω0; I пр.0 – приведенный момент инерции механизма в рассматриваемом положении.

При положении φ1= φ0+ d φ угловая скорость звена приведения ω1, I пр.1 – приведенный момент инерции механизма.

Изменение кинетической энергии механизма ΔЕ за этот промежуток времени будет равно разности работ сил движущих Адв. и сил сопротивления Асопр., выполненных за это время (или избыточной работе ):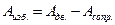

 

ΔЕ = Адв .- Асопр .= Аизб. (4.7)

Здесь ΔЕ = Е1 - Е0 = 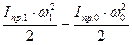, (4.8)

где Е0 и Е1 – величины кинетических энергий механизма при положениях φ0 и φ1 кривошипа,

Адв. = 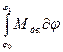, (4.9)

Асопр. = 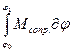, (4.10)

где Мдв. и Мсопр. – приведенные моменты сил движущих и сил сопротивлений.

Подставив (4.8…4.10) в (4.7), получим:

 

(4.11)

 

Из (4.11) выразим угловую скорость кривошипа при положении :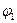

 

 

(4.12)