Свойства гиперболы
1. Фокальное свойство: гипербола – ГМТ (геометрическое место точек), модуль разности расстояний от которых до соответствующих фокусов постоянен и равен 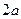 , т.е.
, т.е. 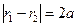 . Доказательство свойства аналогично доказательству фокального свойства эллипса.
. Доказательство свойства аналогично доказательству фокального свойства эллипса.
2. Директориальное свойство: такое же, как и эллипса и доказывается также.
3. Оптическое свойство: гипербола – ГМТ (геометрическое место точек), касательная в которых образует равные острые углы с фокальными радиусами, т.е. 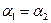 . Другими словами, лучи света, исходящие из одного фокуса
. Другими словами, лучи света, исходящие из одного фокуса 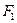 гиперболы, после зеркального отражения от гиперболы кажутся исходящими из другого её фокуса
гиперболы, после зеркального отражения от гиперболы кажутся исходящими из другого её фокуса  (так как касательная проходит между фокусами). Доказывается так же, как и оптическое свойство эллипса.
(так как касательная проходит между фокусами). Доказывается так же, как и оптическое свойство эллипса.
п. 13.3 О гиперболических функциях
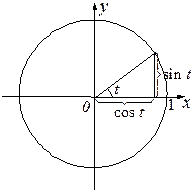 Тригонометрические функции
Тригонометрические функции 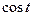 и
и 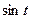 определяются таким образом, что
определяются таким образом, что 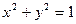 ,
, 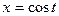 ,
, 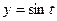 , т.е.
, т.е. 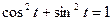 . (
. ( 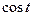 – абсцисса точки
– абсцисса точки 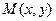 на единичной окружности,
на единичной окружности, 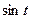 – её ордината).
– её ордината).
| рис.2.50 |
Если рассмотреть равнобочную гиперболу 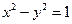 , то можно ввести гиперболические функции
, то можно ввести гиперболические функции 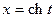 (гиперболический косинус) и
(гиперболический косинус) и 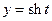 (гиперболический синус) так, что
(гиперболический синус) так, что 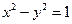 , т.е.
, т.е. 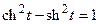 .
.
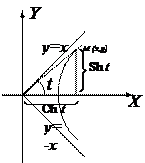 Введём представление о числе
Введём представление о числе 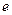 . Рассмотрим все возможные функции
. Рассмотрим все возможные функции 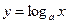 и выберем из них ту, у которой касательная, проведённая через точку
и выберем из них ту, у которой касательная, проведённая через точку 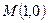 , составляет угол
, составляет угол 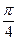 с осью
с осью 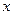 . Основание такой логарифмической функции и есть число
. Основание такой логарифмической функции и есть число 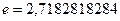 …
…
Покажем, что 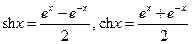 .
.
Функция 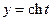 – чётная,
– чётная, 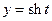 – нечётная функция. Подставим
– нечётная функция. Подставим 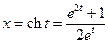 ,
, 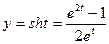 в уравнении гиперболы. Получим
в уравнении гиперболы. Получим
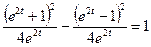 ;
; 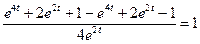 ;
; 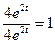 ;
; 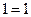 .
.
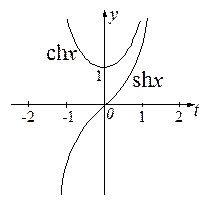 Графики гиперболических функций:
Графики гиперболических функций:
 - котангенс гиперболический.
- котангенс гиперболический.
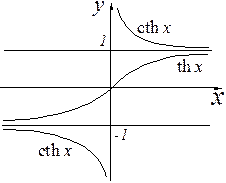
 - тангенс гиперболический.
- тангенс гиперболический.
п. 13.4 Парабола
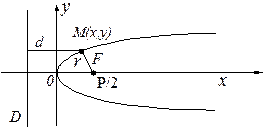 Определение 1. Параболой называется линия
Определение 1. Параболой называется линия 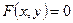 на плоскости, если найдётся такая ДПСК-2 (декартова прямоугольная система координат), в которой её уравнение примет вид
на плоскости, если найдётся такая ДПСК-2 (декартова прямоугольная система координат), в которой её уравнение примет вид 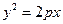 .
.
Величину 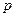 называют фокальным параметром параболы, точку
называют фокальным параметром параболы, точку 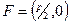 – фокусом, ось
– фокусом, ось 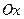 – фокальной осью, прямую
– фокальной осью, прямую 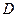 :
: 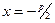 – директрисой.
– директрисой.
Свойства параболы
1. Фокальное свойство: отсутствует.
2. Директориальное свойство: парабола – ГМТ (геометрическое место точек), равноудаленных от фокуса и директрисы, т.е. 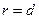 .
.
Доказательство:
Рассмотрим 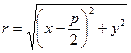 ,
, 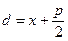 . Тогда
. Тогда 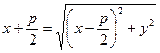 ,
, 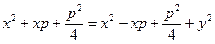 ,
, 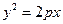 . ■
. ■
3. Оптическое свойство: парабола – ГМТ (геометрическое место точек), в которых касательная образует равные углы с фокальным радиусом 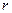 и положительным направлением оси
и положительным направлением оси 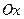 .
.
 Другими словами, лучи света, исходящие из фокуса параболы, после зеркального отражения от параболы, образуют пучок, параллельный оси параболы. И наоборот, все лучи, параллельные фокальной оси, отражаясь от параболы, попадают в фокус параболы.
Другими словами, лучи света, исходящие из фокуса параболы, после зеркального отражения от параболы, образуют пучок, параллельный оси параболы. И наоборот, все лучи, параллельные фокальной оси, отражаясь от параболы, попадают в фокус параболы.
Доказательство:
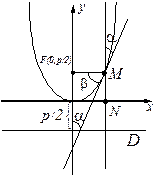 Рассмотрим параболу
Рассмотрим параболу 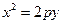 или
или 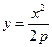 . Покажем, что
. Покажем, что  .
.
Запишем уравнение касательной к параболе, проходящей через точку 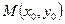 :
: 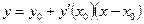 .
.
| рис.2.56 |
Так как 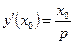 , то
, то
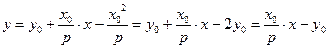 . По директориальному свойству
. По директориальному свойству 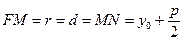 . Отсюда
. Отсюда 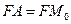 . Следовательно, треугольник
. Следовательно, треугольник 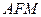 равнобедренный, т.е.
равнобедренный, т.е. 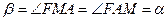 . ■
. ■
п.14 Поверхности второго порядка
п. 14.1 Поверхности вращения
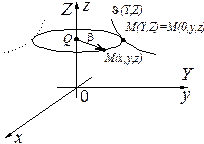
| рис.2.57 |
Рассмотрим в ДПСК-2 (декартова прямоугольная система координат) 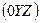 линию
линию 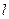 :
: 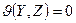 . Совместим с этой ДПСК-2 (декартова прямоугольная система координат) систему ДПСК-3
. Совместим с этой ДПСК-2 (декартова прямоугольная система координат) систему ДПСК-3 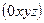 так, что у них совпадают начало координат и оси: ось
так, что у них совпадают начало координат и оси: ось 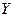 совпадает с осью
совпадает с осью 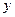 , ось
, ось 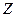 совпадает с осью
совпадает с осью 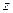 , а ось
, а ось 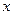 перпендикулярна плоскости
перпендикулярна плоскости 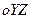 . При вращении линии
. При вращении линии 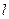 :
: 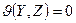 вокруг оси
вокруг оси 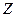 любая точка
любая точка 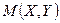 , совпадающая с точкой
, совпадающая с точкой 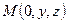 на плоскости
на плоскости 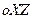 , опишет окружность с радиусом
, опишет окружность с радиусом 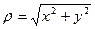 и центром в точке
и центром в точке 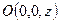 . Таким образом, чтобы получить уравнение поверхности, образованной вращением линии
. Таким образом, чтобы получить уравнение поверхности, образованной вращением линии 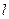 :
: 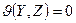 вокруг оси
вокруг оси 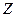 , надо сделать замену переменных:
, надо сделать замену переменных: 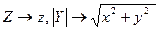 .
.
Соответствующие правила для вращения вокруг других осей сформулировать самостоятельно.
Рассмотрим примеры поверхностей вращения (вокруг оси 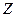 ):
):
1. Эллипсоид вращения эллипса: 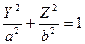 ,
, 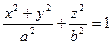 .
.
2. Параболоид вращения параболы: 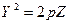 ,
, 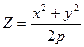 .
.
3. Однополостной гиперболоид получается при вращении гиперболы 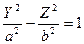 вокруг оси
вокруг оси 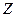 :
: 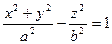 .
.
4. Двуполостный гиперболоид получится при вращении гиперболы 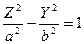 вокруг оси
вокруг оси 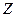 :
: 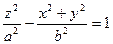 .
.
п. 14.2 Поверхности второго порядка
Если у поверхности вращения заменить 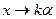 , т.е. сжать все эти поверхности вдоль оси
, т.е. сжать все эти поверхности вдоль оси 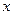 , то получаются общие поверхности второго порядка. Исследовать их легко с помощью метода сечений (некоторые поверхности второго порядка не являются поверхностями вращения).
, то получаются общие поверхности второго порядка. Исследовать их легко с помощью метода сечений (некоторые поверхности второго порядка не являются поверхностями вращения).
| рис.2.58 |
1. Эллипсоид: 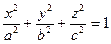 ,
, 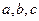 – полуоси эллипсоида. Из
– полуоси эллипсоида. Из 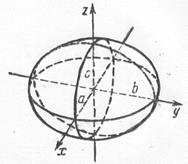 уравнения вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии эллипсоида. Пересечём поверхность плоскостью
уравнения вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии эллипсоида. Пересечём поверхность плоскостью 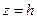 , параллельной плоскости
, параллельной плоскости 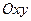 . Тогда уравнение линии, полученной в сечении, имеет вид
. Тогда уравнение линии, полученной в сечении, имеет вид
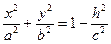 .
.
Полагая 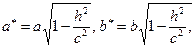 получим уравнение эллипса
получим уравнение эллипса 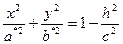 с полуосями
с полуосями 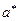 и
и 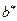 .
.
Аналогичная ситуация возникает при пересечении эллипсоида плоскостями, параллельными плоскостям 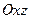 и
и 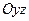 . Заметим, что эллипсоид с равными полуосями:
. Заметим, что эллипсоид с равными полуосями: 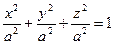 называют сферой.
называют сферой.
Из уравнения вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии эллипсоида.
2. Однополостной гиперболоид.
Из уравнения следует, что координатные плоскости являются плоскостями симметрии однополостного гиперболоида. Пересечение поверхности плоскостью 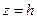 есть эллипс:
есть эллипс: 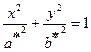 , где
, где 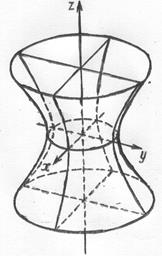
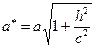 ,
, 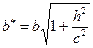 . Сечения однополосного гиперболоида координатными плоскостями
. Сечения однополосного гиперболоида координатными плоскостями  и
и  представляют собой гиперболы, определяемые уравнениями соответственно
представляют собой гиперболы, определяемые уравнениями соответственно
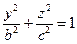 и
и 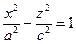 .
.
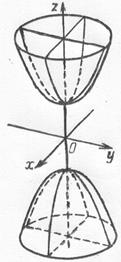
3. Двуполостной гиперболоид:
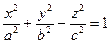 .
.
Из уравнения видно, что координатные плоскости являются плоскостями симметрии, а начало координат центром симметрии двух полосного гиперболоида.
Сечение поверхности плоскостью 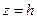 (при
(при 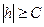 ) представляет собой эллипс
) представляет собой эллипс 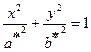 с полуосями
с полуосями 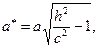

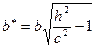 . Сечения двуполостного гиперболоида плоскостями
. Сечения двуполостного гиперболоида плоскостями 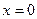 и
и 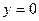 представляют собой гиперболы
представляют собой гиперболы
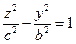 и
и 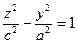 соответственно.
соответственно.
4. Эллиптический параболоид: 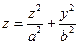 .
.
 Заметим, что координатные плоскости
Заметим, что координатные плоскости 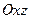 и
и 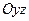 являются плоскостями симметрии эллиптического параболоида. Ось
являются плоскостями симметрии эллиптического параболоида. Ось 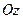 называют осью данной поверхности. Сечение поверхности плоскостью
называют осью данной поверхности. Сечение поверхности плоскостью 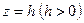 , представляет собой эллипс
, представляет собой эллипс 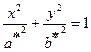 , где
, где 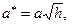
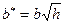 .
.
Сечения эллиптического параболоида плоскостями 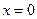 и
и 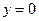 являются параболами
являются параболами 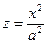 и
и 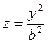 .
.
5. Конус: 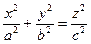 .
.
Отметим, что координатные плоскости являются плоскостями симметрии, я начало координат – центром симметрии конуса. Сечение 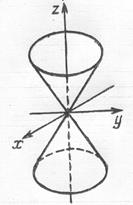 конуса плоскостью
конуса плоскостью 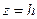 представляет собой эллипс:
представляет собой эллипс: 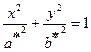 с полуосями
с полуосями 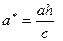 и
и 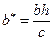 .
.
При пересечении конуса плоскостями 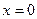 и
и 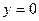 получаются пары пересекающихся прямых
получаются пары пересекающихся прямых
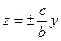 и
и 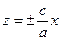 , соответственно, проходящих через начало координат.
, соответственно, проходящих через начало координат.
Цилиндрические поверхности
6. Эллиптический цилиндр: 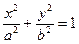 .
. 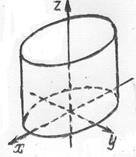 Как видно из уравнения, плоскости
Как видно из уравнения, плоскости 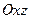 и
и 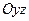 являются плоскостями симметрии данного цилиндра. Сечение поверхности плоскостью
являются плоскостями симметрии данного цилиндра. Сечение поверхности плоскостью 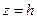 представляет собой эллипс
представляет собой эллипс 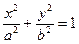 . Сечения цилиндра плоскостями
. Сечения цилиндра плоскостями 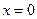 и
и 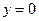 являются парами параллельных прямых
являются парами параллельных прямых 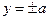 и
и 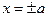 соответственно.
соответственно.
7. Гиперболический цилиндр: 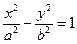 .
.
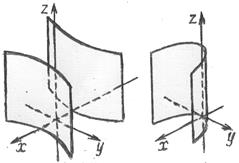 |
8. Параболический цилиндр 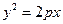 .
.
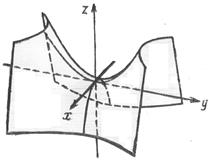 9. Гиперболический параболоид
9. Гиперболический параболоид
| рис.2.655 |
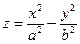 . Из уравнения вытекает, что плоскости
. Из уравнения вытекает, что плоскости  и
и 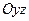 являются плоскостями симметрии. Ось
являются плоскостями симметрии. Ось 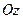 называется осью гиперболического параболоида с плоскостью
называется осью гиперболического параболоида с плоскостью 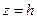 представляет собой гиперболы
представляет собой гиперболы 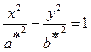 , с полуосями
, с полуосями 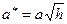 ,
, 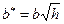 при
при 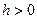 , а при
, а при 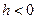 – сопряжённые гиперболы для гипербол
– сопряжённые гиперболы для гипербол 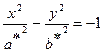 с полуосями
с полуосями 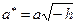 ,
, 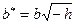 .
.
Заметим, что плоскость 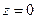 пересекает поверхность по двум прямым
пересекает поверхность по двум прямым 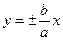 , являющихся асимптотами вышеуказанных гипербол. Сечения плоскостями
, являющихся асимптотами вышеуказанных гипербол. Сечения плоскостями 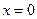 и
и 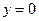 являются параболами
являются параболами 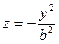 и
и 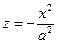 соответственно.
соответственно.








