Векторное произведение в ДПСК
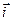
| 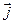
| 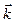
| |
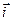
| 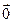
| 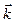
| 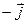
|
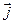
| 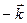
| 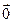
| 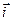
|
| 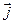
| 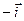
| 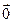
|
Рассмотрим векторы 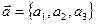 и
и 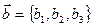 в ДПСК
в ДПСК 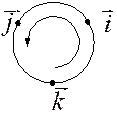
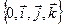 . Для базисных векторов
. Для базисных векторов 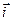 ,
, 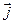 ,
, 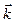 имеем:
имеем: 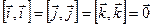 ,
, 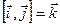 ,
, 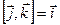 ,
, 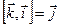 или
или
| рис. 2.34 |
Тогда в силу линейности векторного произведения
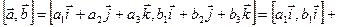
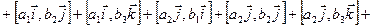
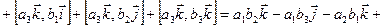
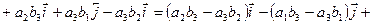
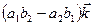 .
.
Итак, 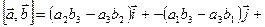
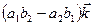 . Для запоминания последней формулы удобно использовать псевдоопределитель:
. Для запоминания последней формулы удобно использовать псевдоопределитель:
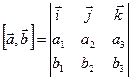 .
.
Раскрывая этот «определитель», стоящий в правой части, по элементам первой строки, получим разложение вектора 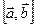 по базису
по базису 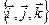 .
.
Пример. Дан  . На сторонах треугольника выбраны
. На сторонах треугольника выбраны 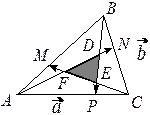 соответственно точки
соответственно точки 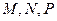 так, чтобы
так, чтобы 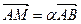 ,
, 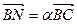 ,
, 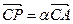 . При каком
. При каком 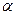 площадь
площадь 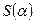 треугольника
треугольника 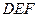 наименьшая?
наименьшая?
Решение:
Пусть 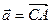 ,
, 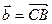 . Тогда
. Тогда 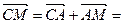
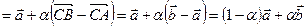 ,
, 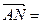
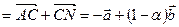 . Поэтому
. Поэтому 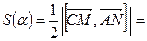
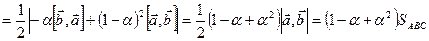 Минимум этого выражения достигается при
Минимум этого выражения достигается при 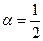 , т. е. в случае, когда
, т. е. в случае, когда 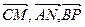 - медианы
- медианы 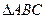 . Этот минимум равен
. Этот минимум равен 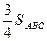 .
.
п. 11 Произведения тройки векторов
п. 11.1 Смешанное произведение векторов
Определение 1. Смешанным произведением векторов 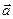 ,
, 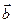 ,
, 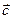 называется скалярное произведение одного из них с векторным произведением двух оставшихся
называется скалярное произведение одного из них с векторным произведением двух оставшихся 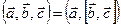 .
.
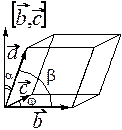 Замечание. Геометрический смысл смешанного произведения. Рассмотрим произвольную тройку некомпланарных векторов
Замечание. Геометрический смысл смешанного произведения. Рассмотрим произвольную тройку некомпланарных векторов  ,
,  ,
, 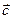 , приведённых к общему началу. Тогда модуль
, приведённых к общему началу. Тогда модуль 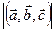 смешанного
смешанного 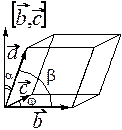 произведения векторов
произведения векторов 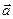 ,
, 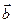 ,
, 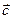 равен объёму параллелепипеда, построенного на этих векторах. Действительно,
равен объёму параллелепипеда, построенного на этих векторах. Действительно, 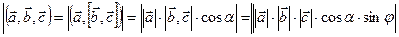
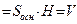 , где
, где 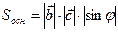 ,
, 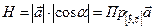 . Заметим, что если тройка векторов
. Заметим, что если тройка векторов 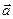 ,
, 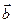 ,
, 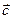 – правая, то
– правая, то 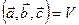 , если
, если 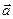 ,
, 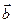 ,
, 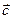 – левая, то
– левая, то 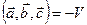 .
.
Свойства смешанного произведения
1. Ассоциативность: 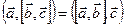 .
.
Доказательство:
Очевидно, что 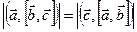 , так как каждая часть равенства выражает объём параллелепипеда, построенного на векторах
, так как каждая часть равенства выражает объём параллелепипеда, построенного на векторах 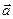 ,
, 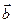 ,
, 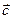 . Заметим, что обе тройки
. Заметим, что обе тройки 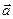 ,
, 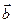 ,
, 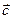 и
и 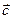 ,
, 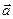 ,
, 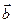 правые, значит
правые, значит
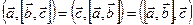 в силу коммутативности скалярного произведения. ■
в силу коммутативности скалярного произведения. ■
2. Правило циклической перестановки:
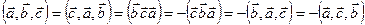 .
.
Доказательство:
Модули всех этих смешанных произведений равны. Первые три смешанных произведения имеют одну ориентацию, последние три – другую. ■
3. Линейность по каждому аргументу:
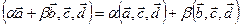 ,
,
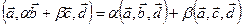 ,
,
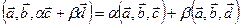 .
.
| Доказательство: |
Поскольку и скалярные, и векторные произведения однородны и дистрибутивны, т.е. линейны, то и смешанное произведение линейно по всем трем векторам. ■
Теорема 1. Критерий компланарности векторов
Векторы 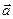 ,
, 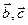 компланарны тогда и только тогда, когда их смешанное произведение
компланарны тогда и только тогда, когда их смешанное произведение 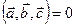 .
.
Доказательство:
Пусть векторы 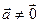 ,
, 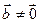 ,
, 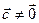 .
.
Необходимость. Путь векторы 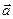 ,
, 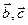 компланарны.
компланарны.
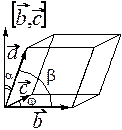 По определению они лежат в одной или параллельных плоскостях. Совмести их начала, тогда все три вектора лежат в одной плоскости, отсюда
По определению они лежат в одной или параллельных плоскостях. Совмести их начала, тогда все три вектора лежат в одной плоскости, отсюда 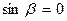 . Следовательно,
. Следовательно, 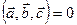 .
.
Достаточность. Пусть 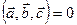 . Тогда либо
. Тогда либо 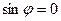 , либо
, либо 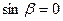 . Если
. Если 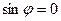 , то векторы
, то векторы 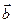 и
и 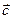 коллинеарные, следовательно, векторы
коллинеарные, следовательно, векторы 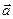 ,
, 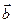 ,
, 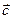 - компланарны.
- компланарны.
Если 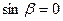 , то вектор
, то вектор 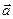 лежит в той же плоскости, что векторы
лежит в той же плоскости, что векторы 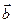 и
и 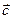 , т.е.
, т.е. 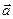 ,
, 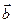 ,
, 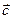 - компланарны. ■
- компланарны. ■
Смешанное произведение в ДПСК
Рассмотрим векторы 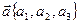 ,
, 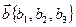 ,
, 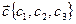 в ДПСК
в ДПСК  . Тогда, учитывая, что
. Тогда, учитывая, что
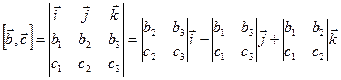 ,
,
получаем 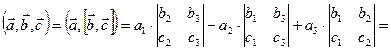
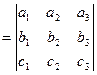 .
.
Пример. При каком 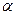 векторы
векторы 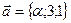 ,
, 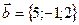 ,
, 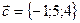 будут компланарны?
будут компланарны?
Решение:
Воспользуемся критерием компланарности. Векторы 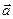 ,
, 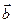 ,
, 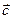 компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда 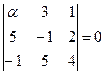 . Вычислим определитель и решим уравнение относительно
. Вычислим определитель и решим уравнение относительно 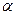 :
: 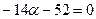 ;
; 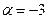 .
.
Пример. Даны векторы 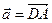 ,
, 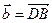 ,
, 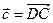 трёх рёбер тетраэдра
трёх рёбер тетраэдра  , выходящих из вершины
, выходящих из вершины  . Найти вектор
. Найти вектор 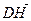 высоты тетраэдра, опущенной из вершины
высоты тетраэдра, опущенной из вершины 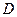 на плоскость
на плоскость 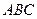 .
.
Решение:
Вектор 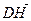 ортогонален плоскости
ортогонален плоскости  , т.е. коллинеарен вектору
, т.е. коллинеарен вектору 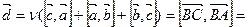


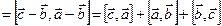 .
. 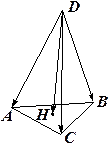 Следовательно, существует такое число
Следовательно, существует такое число 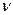 , что
, что 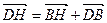 . Вектор
. Вектор 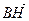 компланарен векторам
компланарен векторам 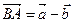 и
и 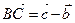 . Тогда найдутся такие числа
. Тогда найдутся такие числа 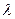 и
и 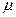 , что
, что 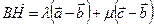 . Получаем для
. Получаем для 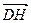 ,
, 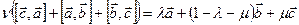 . Умножим обе части равенства скалярно на
. Умножим обе части равенства скалярно на 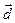 и получим:
и получим: 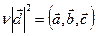 , т.е.
, т.е. 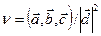 . Таким образом,
. Таким образом,
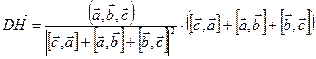 .
.
п. 11.2 Двойное векторное произведение
векторов
Определение 1. Двойным векторным произведением векторов 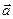 ,
, 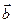 ,
, 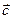 называют вектор
называют вектор 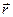 , равный векторному произведению одного из векторов тройки на векторное произведение оставшихся
, равный векторному произведению одного из векторов тройки на векторное произведение оставшихся 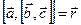 .
.
Замечание. Мнемоническое правило для запоминания: 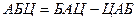 .
.
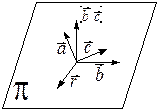 Теорема1.
Теорема1. 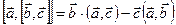 .
.
Доказательство:
| рис. 2.39 |
Из определения векторного произведения вектор 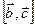 ортогонален плоскости
ортогонален плоскости  . Вектор
. Вектор 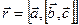 ортогонален плоскости, в которой лежат вектора
ортогонален плоскости, в которой лежат вектора 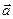 и
и 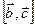 , т.е. лежит в плоскости
, т.е. лежит в плоскости 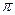 . Таким образом, вектор
. Таким образом, вектор 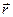 можно разложить по базису
можно разложить по базису 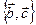 (в силу неколлинеарности векторов
(в силу неколлинеарности векторов 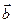 и
и 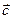 ):
): 
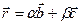 . Умножим последнее равенство скалярно на вектор
. Умножим последнее равенство скалярно на вектор 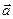 , получим
, получим 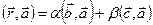 . Так как векторы
. Так как векторы 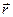 и
и 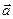 ортогональны, то
ортогональны, то 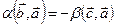 , т.е.
, т.е. 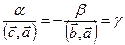 .
.
Итак, 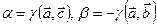 , учитывая коммутативность скалярного произведения. Покажем, что
, учитывая коммутативность скалярного произведения. Покажем, что 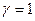 . Введём ДПСК
. Введём ДПСК 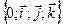 так, чтобы векторы
так, чтобы векторы 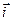 и
и 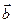 были коллинеарными. Тогда
были коллинеарными. Тогда 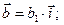
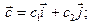
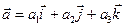 . Рассмотрим произведение
. Рассмотрим произведение 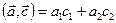 ,
, 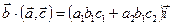 ;
; 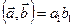 ,
, 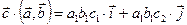 ;
;
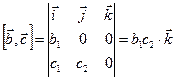 ,
, 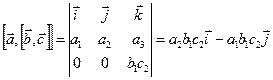 .
.
Сравнивая последнее равенство со следующим 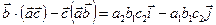 , получаем
, получаем 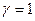 . ■
. ■
п. 12 Основные задачи векторной алгебры
Определение 1. Геометрическим местом точек (ГМТ) на плоскости или в пространстве называется множество точек, обладающих заданным свойством, причём никакие другие точки этим свойством не обладают.
Определение 2. Уравнение 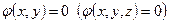 называется уравнением соответствующего ГМТ относительно заданной системы координат, если при подстановке координат точек в уравнение ГМТ получается верное равенство.
называется уравнением соответствующего ГМТ относительно заданной системы координат, если при подстановке координат точек в уравнение ГМТ получается верное равенство.
п. 12.1 Плоскость в пространстве
Характеристика:
 Любая плоскость задаётся своей нормалью
Любая плоскость задаётся своей нормалью 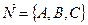 (вектором, ортогональным данной плоскости) и точкой
(вектором, ортогональным данной плоскости) и точкой 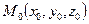 , лежащей на этой плоскости.
, лежащей на этой плоскости.
Базовая задача:
Возьмём произвольную точку 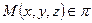 . Вектор
. Вектор 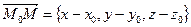 лежит на плоскости
лежит на плоскости 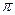 . Так как
. Так как 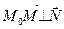 , то
, то 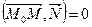 . Тогда
. Тогда 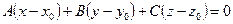 . Раскрывая скобки, получим
. Раскрывая скобки, получим 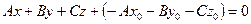 . Обозначим
. Обозначим 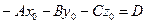 . Тогда уравнение
. Тогда уравнение 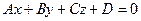 называют общим уравнением плоскости.
называют общим уравнением плоскости.
Существуют и другие уравнения плоскости:
1. Уравнение плоскости в векторной форме: 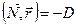 , где
, где 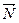 – нормальный вектор данной плоскости,
– нормальный вектор данной плоскости, 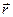 – радиус-вектор точки
– радиус-вектор точки 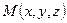 .
. 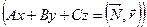
2. Нормальное уравнение плоскости. Так как 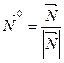 , то
, то 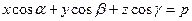 , где:
, где: 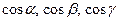 – направляющие косинусы нормального вектора
– направляющие косинусы нормального вектора 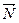 , направленного из начала координат в сторону плоскости;
, направленного из начала координат в сторону плоскости;
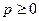 – расстояние от начала координат до плоскости.
– расстояние от начала координат до плоскости.
Нормальное уравнение плоскости получается путём умножения общего уравнения на нормирующий множитель 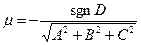 , где
, где 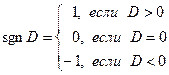 , (signum - знак).
, (signum - знак).
3. Уравнение плоскости в отрезках: 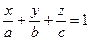 , где
, где 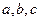 – величины отрезков, которые отсекает плоскость на осях
– величины отрезков, которые отсекает плоскость на осях  ,
,  ,
, 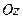 соответственно.
соответственно.
Основные задачи
1. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой.
Пусть точки 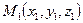 ,
, 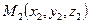 ,
, 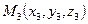 раз
раз 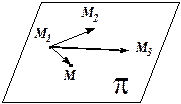 личные и не лежат на одной прямой. Выберем произвольную точку
личные и не лежат на одной прямой. Выберем произвольную точку 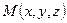 так, чтобы три вектора
так, чтобы три вектора 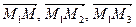 были компланарны. Используем критерий компланарности трёх векторов. Тогда уравнение
были компланарны. Используем критерий компланарности трёх векторов. Тогда уравнение 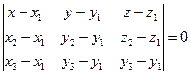 является уравнением искомой плоскости
является уравнением искомой плоскости 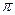 .
.
2. Угол между двумя плоскостями.
Определение 1. Пусть две плоскости 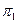 и
и 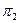 заданы общими уравнениями
заданы общими уравнениями 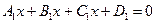 и
и 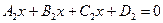 . Под углом между двумя плоскостями
. Под углом между двумя плоскостями 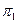 и
и 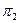 будем понимать угол между нормалями к этим плоскостям. Тогда:
будем понимать угол между нормалями к этим плоскостям. Тогда:
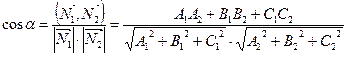 .
.
Условие перпендикулярности плоскостей 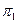 и
и 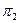 :
: 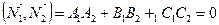 .
.
Условие параллельности плоскостей 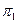 и
и 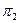 :
: 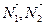 коллинеарные, т.е.
коллинеарные, т.е. 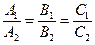 .
.
3. Расстояние от точки до плоскости.
Если плоскость 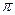 задана нормальным уравнением
задана нормальным уравнением 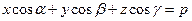 , то отклонением точки
, то отклонением точки 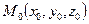 от плоскости
от плоскости 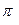 называют
называют 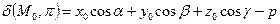 . Знак
. Знак 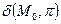 указывает на взаимное расположение точки
указывает на взаимное расположение точки 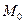 на плоскости
на плоскости 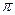 и начала координат, а именно:
и начала координат, а именно:
а) если точка 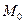 и начало координат лежат по разные стороны от плоскости
и начало координат лежат по разные стороны от плоскости 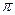 , то
, то 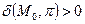 ,
,
б) если 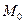 и начало координат находятся по одну сторону от плоскости
и начало координат находятся по одну сторону от плоскости 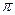 , то
, то 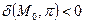 .
.
4. Расстояние 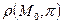 от точки
от точки 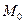 до плоскости
до плоскости 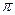 определяется равенством
определяется равенством 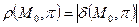 .
.
Итак, 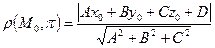 .
.
п. 12.2 Прямая на плоскости
Характеристики:
· нормальный вектор и точка;
· направляющий вектор и точка.
Базовые задачи:
1. Если на плоскости задана некоторая система координат, то прямую 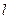 можно провести через точку
можно провести через точку 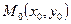 перпендикулярно вектору
перпендикулярно вектору 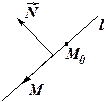
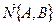 , называемого
, называемого
нормалью к данной прямой. Тогда, выбрав произвольную точку 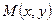 так, чтобы векторы
так, чтобы векторы  и
и 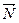 были перпендикулярны, получим уравнение прямой
были перпендикулярны, получим уравнение прямой 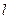 :
:
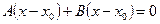 ,
, 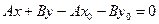 .
.
Обозначим через 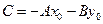 . Тогда уравнение
. Тогда уравнение 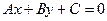 называется общим уравнением прямой
называется общим уравнением прямой 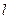 .
.
2. Проведём прямую  через точку
через точку 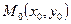 параллельно вектору
параллельно вектору 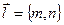 , который называют направляющим вектором прямой
, который называют направляющим вектором прямой  . Выберем произвольную точку
. Выберем произвольную точку 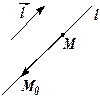
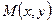 так, чтобы векторы
так, чтобы векторы 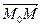 и
и 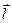 были коллинеарными. Тогда
были коллинеарными. Тогда 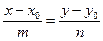 – каноническое уравнение прямой.
– каноническое уравнение прямой.
Из последнего уравнения также можно получить общее уравнение прямой 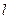 , заметив, что векторы
, заметив, что векторы 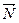 и
и 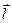 перпендикулярны, причём
перпендикулярны, причём 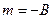 ,
, 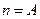 .
.
Другие уравнения прямой:
1. Теперь проведём прямую 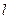 через точки
через точки 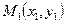 и
и 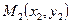 .
. 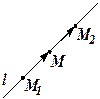 Выберем произвольную точку
Выберем произвольную точку  так, чтобы векторы
так, чтобы векторы  и
и  были коллинеарными. Тогда уравнение
были коллинеарными. Тогда уравнение 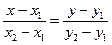 задаёт прямую
задаёт прямую 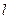 , проходящую через точки
, проходящую через точки 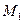 и
и 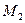 .
.
2. Преобразуем последнее равенство:
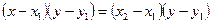 ;
; 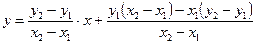 . Тогда уравнение
. Тогда уравнение 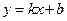 также задаёт прямую
также задаёт прямую 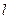 , где:
, где:
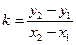 - угловой коэффициент, причём
- угловой коэффициент, причём 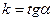 (
( 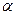 - угол наклона прямой
- угол наклона прямой 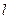 к оси
к оси  );
);
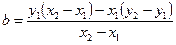 - свободный коэффициент, равный длине отрезка, отсекаемого прямой от оси
- свободный коэффициент, равный длине отрезка, отсекаемого прямой от оси  .
.
Аналогично п. 12.1 можно получить нормальное уравнение прямой 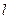 и уравнение данной прямой в отрезках.
и уравнение данной прямой в отрезках.
Угол между двумя прямыми
Пусть две прямые 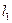 и
и 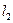 заданы общими или каноническим уравнениями. Тогда угол между прямыми можно найти следующим образом:
заданы общими или каноническим уравнениями. Тогда угол между прямыми можно найти следующим образом:
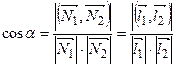 ,
, 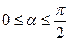 .
.
Если же прямая задана в виде 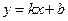 , где
, где 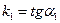 и
и 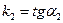 - угловые коэффициенты прямых
- угловые коэффициенты прямых 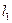 и
и 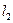 соответственно, то:
соответственно, то:
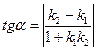 (формула тангенса разности двух углов).
(формула тангенса разности двух углов).
Условие перпендикулярности:
1) 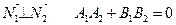 ;
;
2) 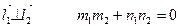 ;
;
3) 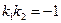 .
.
Условие параллельности:
1) 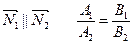 ;
;
2) 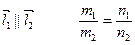 ;
;
3) 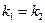 .
.
Расстояние от точки до прямой
Аналогично п. 12.1 расстояние от точки 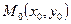 до прямой
до прямой 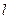 определяется равенством
определяется равенством 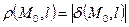 , где
, где 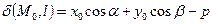 .
.
Итак, 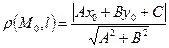 .
.
п. 12.3 Прямая в пространстве
Характеристики: направляющий вектор и точка.
Базовая задача:
| рис. 2.45 |
Проведём прямую  через точку
через точку  , параллельно
, параллельно 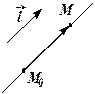 данному направляющему вектору
данному направляющему вектору 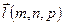 . Выберем для этого произвольную точку
. Выберем для этого произвольную точку 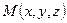 , лежащую на прямой
, лежащую на прямой 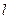 . Тогда векторы
. Тогда векторы 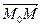 и
и 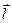 коллинеарные. Следовательно,
коллинеарные. Следовательно, 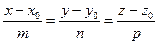 .
.
Последние равенства называют каноническим уравнением прямой. Из канонического задания прямой 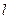 можно получить параметрические уравнения прямой:
можно получить параметрические уравнения прямой: 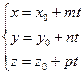 .
.
Прямую 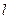 в пространстве можно рассматривать как пересечение двух плоскостей
в пространстве можно рассматривать как пересечение двух плоскостей 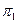 и
и 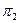
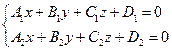 .
.
Перейдём к каноническому заданию прямой 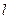 . Для этого надо задать направляющий вектор
. Для этого надо задать направляющий вектор 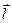 и точку
и точку 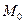 , через которую проходит данная прямая. Заметим, что вектор
, через которую проходит данная прямая. Заметим, что вектор 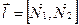 (в силу определения векторного произведения). При общем рас положении данных плоскостей они пересекут какую-либо из координатных плоскостей, например,
(в силу определения векторного произведения). При общем рас положении данных плоскостей они пересекут какую-либо из координатных плоскостей, например, 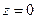 ,
, 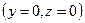 . Тогда
. Тогда
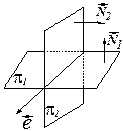
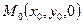 - точка пересечения плоскостей
- точка пересечения плоскостей 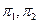 и
и 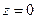 . Эта точка будет лежать и на прямой
. Эта точка будет лежать и на прямой 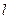 . В силу неоднородности выбора точки
. В силу неоднородности выбора точки 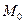 обратная задача не ставится.
обратная задача не ставится.
Угол между прямыми
Заметим, что угол между двумя прямыми можно определить только в том случае, если эти прямые лежат в одном плоскости.
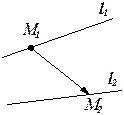 Рассмотрим две прямые
Рассмотрим две прямые 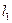 и
и 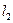 , произвольно расположенные в пространстве:
, произвольно расположенные в пространстве:
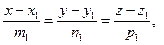
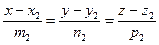 .
.
Тогда для того, чтобы прямые 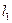 и
и 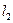 лежали в одной плоскости, необходимо, чтобы векторы
лежали в одной плоскости, необходимо, чтобы векторы 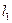 ,
, 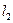 и
и 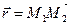 были компланарными. В силу критерия компланарности должно выполняться равенство
были компланарными. В силу критерия компланарности должно выполняться равенство 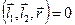 . Тогда угол между прямыми
. Тогда угол между прямыми 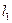 и
и 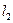 определяется как угол между соответствующими направляющими векторами:
определяется как угол между соответствующими направляющими векторами: 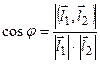 .
.
В частности, прямые 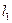 и
и 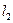 :
:
· параллельны, если 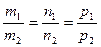 ;
;
· перпендикулярны, если 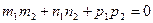 .
.
Если же смешанное произведение 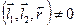 , то прямые
, то прямые 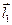 и
и  называются скрещивающимися.
называются скрещивающимися.
Угол между прямой и плоскостью
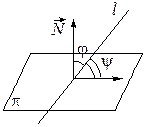 Углом между прямой и плоскостью называют угол
Углом между прямой и плоскостью называют угол 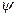 между прямой
между прямой 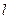 и её ортогональной проекцией на плоскость
и её ортогональной проекцией на плоскость 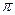
 .
.
п.13 Линии второго порядка
 п.13.1 Эллипс
п.13.1 Эллипс
Всякий знает, что такое кривая, пока не вы-
учится математике настолько, что в конец
запутается в бесчисленных исключениях.
Ф. Клейн
| рис.2.47 |
Определение 1. Эллипсом называется линия 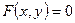 на плоскости, если найдётся такая ДПСК-2 (декартова прямоугольная система координат), в которой уравнение примет вид
на плоскости, если найдётся такая ДПСК-2 (декартова прямоугольная система координат), в которой уравнение примет вид 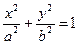 .
. 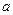 и
и 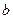 называют полуосями эллипса (для определённости
называют полуосями эллипса (для определённости 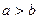 ),
), 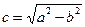 – линейным эксцентриситетом, точки
– линейным эксцентриситетом, точки 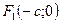 и
и 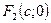 – фокусами, а ось
– фокусами, а ось 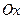 – фокальной осью. Величину
– фокальной осью. Величину 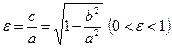 , называемую эксцентриситетом эллипса, можно рассматривать как меру его вытянутости: чем больше
, называемую эксцентриситетом эллипса, можно рассматривать как меру его вытянутости: чем больше 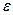 , тем меньше отношение
, тем меньше отношение 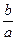 . Прямые
. Прямые 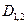 , задаваемые
, задаваемые 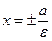 , называют директрисами эллипса.
, называют директрисами эллипса.
Свойства эллипса
1. Фокальное свойство: эллипс – это ГМТ (геометрическое место точек), сумма расстояний которых до фокусов постоянна и равна 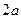 .
.
Доказательство:
Рассмотрим 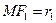 и
и 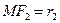 . Покажем, что
. Покажем, что 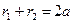 .
.
Найдём 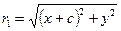 и
и 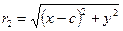 . Тогда
. Тогда 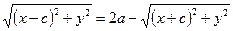 ;
;
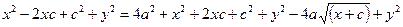 ;
; 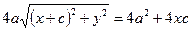 ;
; 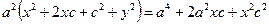 ;
; 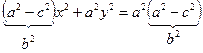 . Разделим обе части равенства на
. Разделим обе части равенства на 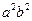 , получим
, получим 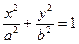 . ■
. ■
2. Директориальное свойства: эллипс – ГМТ (геометрическое место точек), отношение расстояний от которых до фокусов и до соответствующих директрис равно 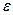 .
.
Доказательство:
Обозначим через 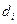 расстояние от точки
расстояние от точки 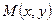 до директрисы
до директрисы 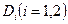 . Покажем, что
. Покажем, что 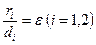 .
.
Пусть 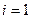 . Тогда
. Тогда 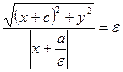 ;
; 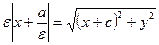 . Так как
. Так как 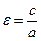 , то
, то 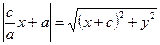 ,
, 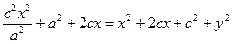 ;
;
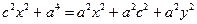 ;
; 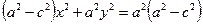
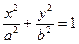 . ■
. ■
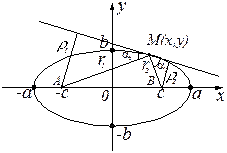 3. Оптическое свойство: эллипс – ГМТ (геометрическое место точек), касательные в которых образуют равные острые углы с фокальными радиусами
3. Оптическое свойство: эллипс – ГМТ (геометрическое место точек), касательные в которых образуют равные острые углы с фокальными радиусами 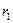 и
и 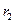 , т.е.
, т.е. 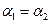 .
.
Другими словами, лучи света, исходящие из одного фокуса 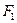 эллипса, после зеркального отражения от эллипса проходят через второй фокус
эллипса, после зеркального отражения от эллипса проходят через второй фокус 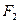 .
.
Касательная в любой точке 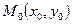 эллипса образует с фокальными радиусами острые одинаковые углы. Это свойство называется оптическим, т.к. все лучи, выходящие из одного фокуса, после отражения оказывается в другом (так как угол падения равен углу отражения).
эллипса образует с фокальными радиусами острые одинаковые углы. Это свойство называется оптическим, т.к. все лучи, выходящие из одного фокуса, после отражения оказывается в другом (так как угол падения равен углу отражения).
Доказательство:
1. Получим сначала уравнение касательной к эллипсу в любой точке 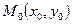 эллипса. Из уравнения эллипса
эллипса. Из уравнения эллипса 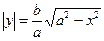 , т.е.
, т.е. 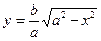 , если
, если 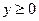 , и
, и 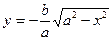 , если
, если 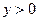 . Тогда и в том и в другом случае
. Тогда и в том и в другом случае 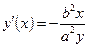 ,
, 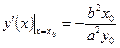 .
.
Таким образом, уравнение касательной к кривой 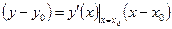 в данном случае имеет вид
в данном случае имеет вид 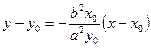 . Умножив это уравнение на
. Умножив это уравнение на 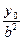 , раскрыв скобки и учтя, что
, раскрыв скобки и учтя, что 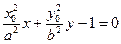 –получим уравнение касательной к эллипсу.
–получим уравнение касательной к эллипсу.
2. Найдём уравнение  от точки
от точки 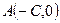 до касательной. Это расстояние
до касательной. Это расстояние 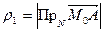 , где
, где 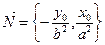 .
.
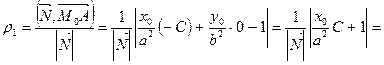
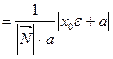 .
.
Но из директориального свойства фокальный радиус 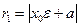 . Таким образом,
. Таким образом, 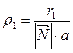 . Тогда
. Тогда 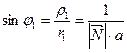 .
.
Проделав аналогичные выкладки, получим, что 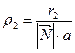 , т.е.
, т.е. 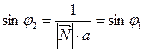 .
.
п. 13.2 Гипербола
Определение 1. Гиперболой называется линия 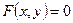 на плоскости, если найдётся такая ДПСК-2 (декартова прямоугольная система координат), в которой её уравнение примет вид
на плоскости, если найдётся такая ДПСК-2 (декартова прямоугольная система координат), в которой её уравнение примет вид 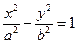 .
.
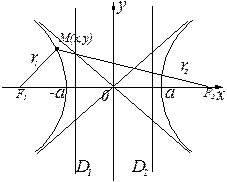
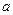 и
и 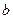 – полуоси,
– полуоси, 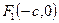 ,
, 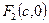 – фокусы,
– фокусы, 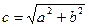 линейный эксцентриситет, ось
линейный эксцентриситет, ось 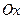 – фокальная ось,
– фокальная ось, 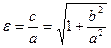 – эксцентриситет, причём
– эксцентриситет, причём 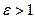 характеризует величину раствора угла между асимптотами гиперболы
характеризует величину раствора угла между асимптотами гиперболы 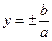 . Прямые
. Прямые 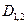 :
: 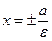 являются директрисами гиперболы.
являются директрисами гиперболы.








