Теорема 2. О делении отрезка в данном отношении
Пусть в ДПСК-3 задан отрезок 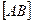 , т.е.
, т.е. 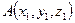 ,
, 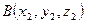 . Тогда точка
. Тогда точка 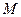 , такая, что
, такая, что 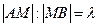 , имеет координаты
, имеет координаты 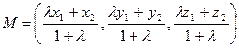 .
.
Доказательство:
Пусть точки 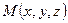 и
и 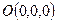 - начало координат. Тогда
- начало координат. Тогда 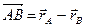 ,
, 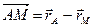 ,
, 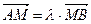 , где
, где 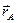 и
и 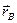 - радиус-векторы точек.
- радиус-векторы точек.
Получим, что 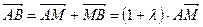 . Так как
. Так как 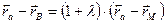 , то
, то 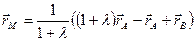 или
или 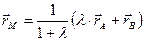 . ■
. ■
п. 6 Свойства проекций
Определение 1. Осью 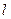 называется прямая
называется прямая 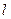 с выбранным на ней направлением.
с выбранным на ней направлением.
Определение 2. Геометрической проекцией вектора 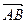 называется вектор
называется вектор 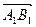 , где
, где 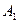 и
и 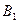 – ортогональные проекции точек А и В на ось
– ортогональные проекции точек А и В на ось 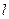 .
.
|
рис. 2.18 |
Определение 3 Алгебраической проекцией вектора 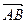 на ось
на ось 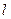 называется число, равное длине
называется число, равное длине 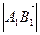 , взятое со знаком “
, взятое со знаком “ 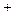 ”, если
”, если 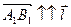 , и со знаком “-”, если
, и со знаком “-”, если 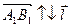 . Обозначается Прl
. Обозначается Прl 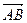 .
.
Теорема1. 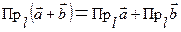 .
.
Доказательство:
Так как 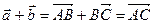 , то
, то 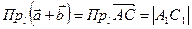 . С другой стороны,
. С другой стороны, 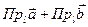 =
= 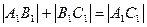 . ■
. ■
Теорема 2. 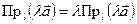 .
.
Доказательство:
Пусть 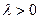 . Перенесём вектор
. Перенесём вектор  так, что его начало находилось на прямой
так, что его начало находилось на прямой 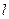 . Тогда треугольники
. Тогда треугольники 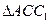 и
и 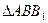 подобны. Если
подобны. Если 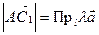 , а
, а 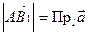 , то
, то 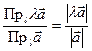 . Отсюда
. Отсюда 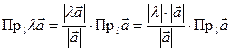 .
. 
| рис. 2.20 |
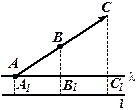 Так как
Так как 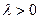 , то
, то 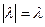 . Значит,
. Значит, 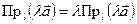 .
.
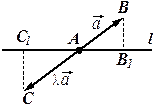 Если же
Если же 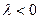 , то треугольники
, то треугольники 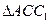 и
и 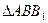 так же подобны. Но
так же подобны. Но 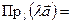
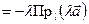 . ■
. ■
| рис. 2.21 |
Теорема 3. 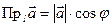 , где
, где 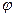 – угол между вектором
– угол между вектором  и положительным направлением оси
и положительным направлением оси 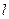 .
.
Доказательство:
| рис. 2.22 |
1. Угол 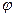 – острый, тогда очевидно, что
– острый, тогда очевидно, что 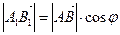 , т.е.
, т.е. 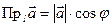 .
.
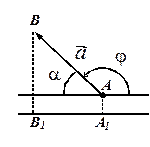 2. Угол
2. Угол 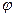 – тупой. Так как
– тупой. Так как 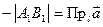 ,
, 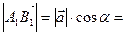
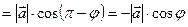 , то
, то 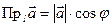 . ■
. ■
п. 7 Скалярное произведение векторов
Определение 1. Скалярным произведением векторов  и
и  называется операция (результат операции), ставящая в соответствии упорядоченной паре векторов
называется операция (результат операции), ставящая в соответствии упорядоченной паре векторов  и
и  скаляр, равный произведению длин векторов на косинус угла между ними.
скаляр, равный произведению длин векторов на косинус угла между ними. 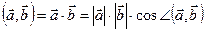 .
.
Замечание. Из определения скалярного произведения, следует, что 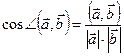 .
.
Замечание. Заметим, что 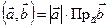 . Если взять вектор
. Если взять вектор  такой, что
такой, что 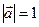 , то
, то 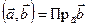 . Таким образом, скалярное произведение одного вектора на другой, имеющий единичную длину, равно проекции первого вектора на направление, определяемое вторым. В этом заключается геометрический смысл скалярного произведения.
. Таким образом, скалярное произведение одного вектора на другой, имеющий единичную длину, равно проекции первого вектора на направление, определяемое вторым. В этом заключается геометрический смысл скалярного произведения.
Замечание. Механический смысл скалярного произведения. Если рассмотреть действия силы 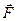 на материальную точку при её перемещении по вектору
на материальную точку при её перемещении по вектору 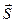 , то работа
, то работа 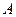 , совершаемая этой силой равна:
, совершаемая этой силой равна: 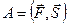 .
.
Свойства скалярного произведения:
1. Коммутативность: 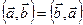 .
.
Доказательство: 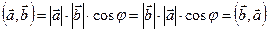 . ■
. ■
2. Унитарность: 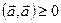 , причём
, причём 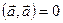 тогда и только тогда, когда
тогда и только тогда, когда 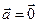 .
.
Доказательство: 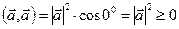 . ■
. ■
3. Однородность: 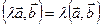 .
.
Доказательство: 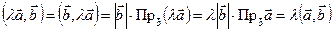 . ■
. ■
4. Дистрибутивность: 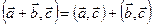 .
.
Доказательство: 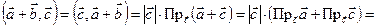
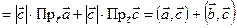 . ■
. ■
Замечание. « однородность + дистрибутивность = линейность».
Теорема1. Критерий ортогональности
Пусть векторы 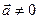 и
и 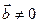 . Тогда
. Тогда 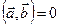 тогда и только тогда, когда
тогда и только тогда, когда 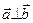 .
.
Пример. В треугольнике 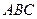 медиана
медиана 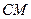 перпендикулярна биссектри
перпендикулярна биссектри 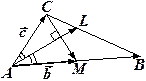 се
се 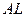 , причём
, причём 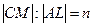 . Найти угол
. Найти угол 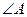 .
.
Решение:
Обозначим 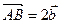 ,
, 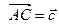 ,
, 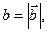
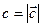 и
и 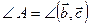 . Тогда
. Тогда 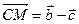 . Выразим
. Выразим 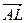 .
.
Известно, что биссектриса угла делит противолежащую сторону в отношении, равном отношении длин прилежащих сторон. Таким образом, 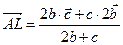 . По условию,
. По условию, 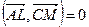 , т.е.
, т.е. 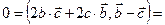
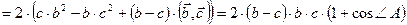 .
.
Так как 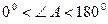 ,
, 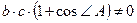 , то
, то 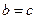 . (В этом можно было убедиться и геометрически: по условию задачи, в
. (В этом можно было убедиться и геометрически: по условию задачи, в 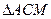 биссектриса
биссектриса 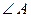 является и высотой, а значит,
является и высотой, а значит, 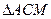 – равнобедренный, т.е.
– равнобедренный, т.е. 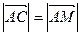 ).
).
Таким образом, 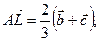
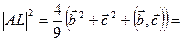
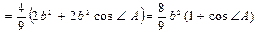 ,
, 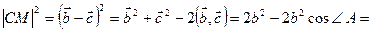
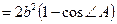 . Следовательно,
. Следовательно, 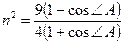 . Отсюда находим
. Отсюда находим 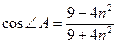 .
.
п. 8 Скалярное произведение в ДПСК
Рассмотрим векторы 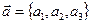 и
и 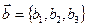 в ДПСК
в ДПСК 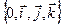 . Из определения скалярного произведения для базисных векторов имеем:
. Из определения скалярного произведения для базисных векторов имеем: 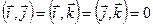 ,
, 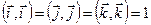 или
или
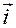
| 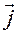
| 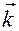
| |
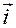
| 1 | 0 | 0 |
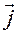
| 0 | 1 | 0 |
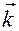
| 0 | 0 | 1 |
Тогда
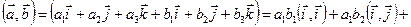
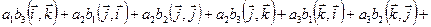
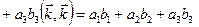 .
.
Итак, 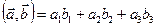 . Заметим, что
. Заметим, что 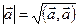 . Тогда
. Тогда 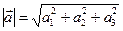 , а также
, а также 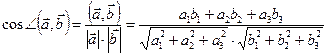 .
.
Наличие обратной операции
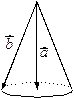 Пусть даны вектор
Пусть даны вектор  и скалярное произведение
и скалярное произведение 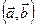 . Можно ли найти вектор
. Можно ли найти вектор  ?
?
Как было показано, 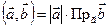 . Все векторы
. Все векторы  лежат на конусе, осью которого является носитель вектор
лежат на конусе, осью которого является носитель вектор  (прямая, на которой лежит вектор), т.е. таких векторов
(прямая, на которой лежит вектор), т.е. таких векторов  бесконечно много.
бесконечно много.
Таким образом, обратная операция не определена.
п. 9 Орт вектора. Направляющие косинусы вектора
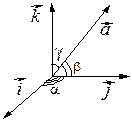 Определение 1. Косинусы углов, которые вектор
Определение 1. Косинусы углов, которые вектор  образует с базисными
образует с базисными 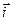 ,
, 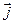 ,
, 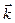 , называются направляющими косинусами вектора
, называются направляющими косинусами вектора  . Обозначают
. Обозначают 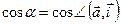 ,
, 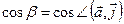 ,
, 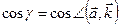 .
.
Определение 2. Ортом вектора называется вектор  , имеющий единичную длину и тоже направление, что и вектор
, имеющий единичную длину и тоже направление, что и вектор  :
: 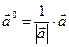 .
.
Покажем, что координатами орта 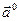 вектора
вектора  являются его направляющие косинусы.
являются его направляющие косинусы.
Пусть 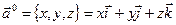 . Рассмотрим
. Рассмотрим 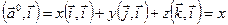 . С другой стороны,
. С другой стороны, 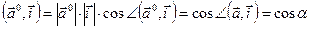 . Следовательно,
. Следовательно, 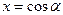 . Аналогично можно показать, что
. Аналогично можно показать, что 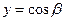 ,
, 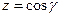 . Заметим, что
. Заметим, что 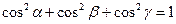 .
.
п. 10 Векторное произведение векторов
Определение 1. Рассмотрим некоторую произвольную тройку некомпланарных векторов  ,
,  ,
,  , приведённых к точке
, приведённых к точке 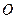 . Тройка векторов
. Тройка векторов 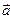 ,
,  ,
,  называется правой, если для неё выполняется правило буравчика: глядя с конца вектора
называется правой, если для неё выполняется правило буравчика: глядя с конца вектора  и
и  , можно увидеть, что кратчайший поворот от
, можно увидеть, что кратчайший поворот от  к
к  происходит против часовой стрелки.
происходит против часовой стрелки.
Определение 2. Векторным произведением векторов называется операция (ре 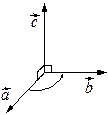 зультат операции), которая любой упорядоченной паре векторов
зультат операции), которая любой упорядоченной паре векторов  и
и  ставит в соответствие вектор
ставит в соответствие вектор 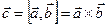 , обладающий следующими свойствами:
, обладающий следующими свойствами:
1) 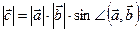 ;
;
|
|
2) вектор  ортогонален каждому
ортогонален каждому
из  и
и  ;
;
3)  ,
,  ,
,  – правая тройка;
– правая тройка;
4) если  и
и  - коллинеарные, то
- коллинеарные, то  =
= 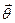 .
.
Замечание. Геометрический смысл векторного произведения двух векто 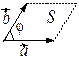 ров
ров  и
и  состоит в том, что модуль
состоит в том, что модуль 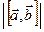 равен площади
равен площади 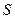 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах  и
и  .
.
Замечание. Механический смысл векторного произведения. Если вектор 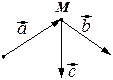
 изображает приложенную в некоторой точке М силу, а вектор
изображает приложенную в некоторой точке М силу, а вектор
 идёт из некоторой точки О в точку М, то вектор
идёт из некоторой точки О в точку М, то вектор 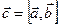 представляет собой момент силы
представляет собой момент силы  относительно точки О.
относительно точки О.
Свойства векторного произведения:
1. Антикоммутативность: 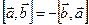 .
.
Доказательство:
Положим 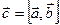 ,
, 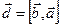 . По определению векторы
. По определению векторы  и
и 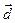 имеют одинаковую длину. Также в силу того, что оба вектора
имеют одинаковую длину. Также в силу того, что оба вектора  и
и 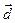 ортогональны к плоскости, определяемой векторами
ортогональны к плоскости, определяемой векторами  и
и  , вектор
, вектор  коллинеарен вектору
коллинеарен вектору 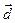 . Тогда либо
. Тогда либо 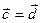 , либо
, либо 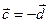 . Если бы имело место первое равенство, то по определению, обе тройки
. Если бы имело место первое равенство, то по определению, обе тройки  ,
,  ,
,  и
и  ,
,  ,
,  оказались бы правыми, но это невозможно. Итак,
оказались бы правыми, но это невозможно. Итак, 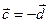 . ■
. ■
2. Однородность: 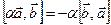 .
.
Доказательство:
Положим 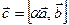 ,
, 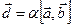 . Пусть векторы
. Пусть векторы  и
и  не коллинеарные и
не коллинеарные и 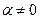 . Обозначим
. Обозначим 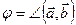 и
и 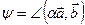 . По определению
. По определению 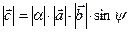 ,
, 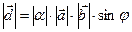 .
.
Возможны два случая:
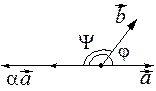
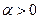 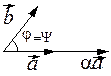
| 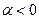 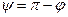
|
| Рис. 2.30 | |
В обоих случаях 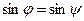 , тогда
, тогда 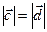 . Далее, заметим, что векторы
. Далее, заметим, что векторы  и
и 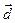 коллинеарные. Остаётся проверить, что эти векторы имеют одинаковое направление.
коллинеарные. Остаётся проверить, что эти векторы имеют одинаковое направление.
Пусть 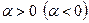 , тогда векторы
, тогда векторы 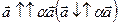 , а значит и векторы
, а значит и векторы 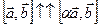
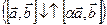 . Итак,
. Итак, 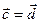 . ■
. ■
3. Дистрибутивность:
Доказательство:
Для доказательства приведём две леммы.
Лемма 1. Векторное произведение произвольного вектора 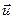 плоскости
плоскости 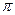 на единичный вектор
на единичный вектор 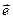 , ортогональный плоскости
, ортогональный плоскости 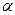 , поворачивает вектор
, поворачивает вектор 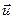 на угол
на угол 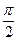 по часовой стрелке, если смотреть с конца вектор
по часовой стрелке, если смотреть с конца вектор 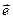 .
.
Доказательство:
По определению 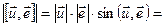
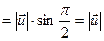 , причём вектор
, причём вектор 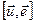 ортогонален векторам
ортогонален векторам 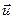 и
и 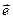 , значит, он лежит на плоскости
, значит, он лежит на плоскости 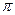 . Тройка векторов
. Тройка векторов 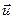 ,
, 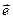 ,
, 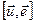 правая, следовательно, поворот от вектора
правая, следовательно, поворот от вектора 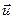 к вектору
к вектору 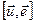 совершается на
совершается на 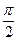 по часовой стрелке, если смотреть с конца вектора
по часовой стрелке, если смотреть с конца вектора 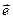 . ■
. ■
Лемма 2. Векторное произведение произвольного вектора 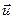 на единичный вектор
на единичный вектор 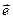 равно
равно 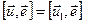 , где
, где 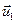 – геометрическая проекция вектора
– геометрическая проекция вектора 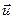 на плоскость
на плоскость 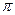 , ортогональную вектору
, ортогональную вектору 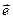 .
.
Доказательство:
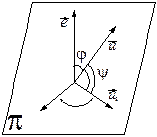 По определению векторного произведения векторы
По определению векторного произведения векторы 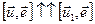 . Рассмотрим их модули:
. Рассмотрим их модули: 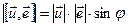 ;
;
|
|
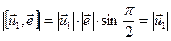 . По условию
. По условию 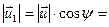
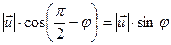 . ■
. ■
Теперь вернёмся к доказательству дистрибутивности 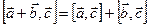 . Для простоты рассмотрим вместо вектора
. Для простоты рассмотрим вместо вектора 
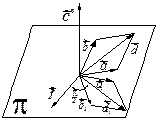 его орт
его орт 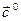 . Пусть векторы
. Пусть векторы  ,
,  ,
,  некомпланарные. Обозначим
некомпланарные. Обозначим 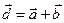 ,
, 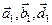 – геометрические проекции векторов
– геометрические проекции векторов 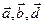 на плоскость
на плоскость 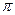 ортогональному вектору
ортогональному вектору  . Тогда по лемме 2 имеем
. Тогда по лемме 2 имеем 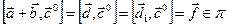 , причём вектор
, причём вектор 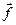 получен поворотом вектора
получен поворотом вектора 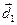 на угол
на угол 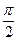 по часовой стрелке (по лемме 1).
по часовой стрелке (по лемме 1).
Аналогично, 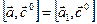 и
и 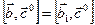 , причём векторы
, причём векторы 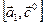 и
и 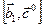 получены поворотами векторов
получены поворотами векторов 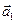 и
и 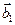 на угол
на угол 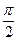 по часовой стрелке, соответственно. Тогда сумма
по часовой стрелке, соответственно. Тогда сумма 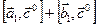 даёт нам вектор
даёт нам вектор 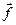 , т.е.
, т.е. 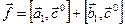 .
.
Таким образом, мы показали, что 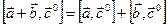 . Умножим обе части равенства на
. Умножим обе части равенства на 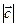 , получим:
, получим: 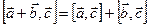 . ■
. ■
Теорема1. Критерий коллинеарности
Векторы  и
и  коллинеарные тогда и только тогда, когда
коллинеарные тогда и только тогда, когда 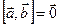 . (доказать самостоятельно)
. (доказать самостоятельно)








