Необходимость. Пусть вектора и коллинеарные. Тогда по определению они лежат на одной или параллельных прямых. С помощью параллельного переноса совместим начала векторов и . Тогда , где
|
рис. 2.13 |
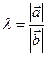, если 
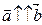(сонаправлены), или 
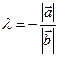, если 
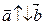; (котранаправлены). (Рис. 2.13).
Достаточность. Пусть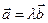 
. Тогда по определению произведения вектора на числа получаем коллинеарность векторов 
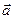и 
. ■
Определение 2. Базисом на плоскости будем называть всякую упорядоченную пару неколлинеарных векторов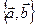 
. Совокупность фиксированной точки 
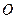плоскости и произвольного базиса 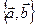на плоскости, приведенного к этой точке, называется аффинной системой координат (АСК) 
.
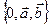Теорема2. Пусть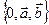 
некоторая АСК на плоскости. Тогда любой вектор 
этой плоскости можно представить в виде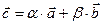 
, 
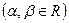и при том единственным образом.
Доказательство:
Покажем существование разложения вектора . Совместим начало вектора с точкой .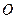
Проведём через конец вектора прямые, параллельные 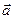и . Тогда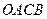 
– параллелограмм. Отсюда 
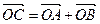. Но векторы 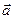и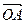 
коллинеарные, значит 
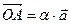. Аналогично, векторы 
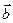и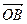 
коллинеарные, значит 
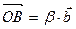. Тогда 
.
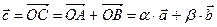Теперь докажем единственность разложения.
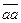. Пусть существует два разложения по базису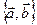 
: 
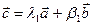и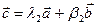 
такие, что 
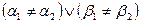. Тогда 
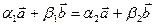или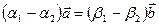 
.
Если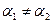 
, то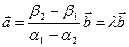 
, что означает коллинеарность векторов 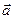и и противоречит условию.
Аналогично, если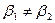 
, то получим коллинеарность 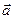и , что противоречит условию. Таким образом,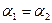 
, 
. ■
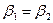Такое представление вектора называется разложением по базису 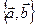, а числа 
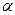и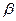 
называются координатами в АСК 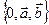. Вектор в этом случае можно записать так: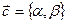 
.
Замечание. Если векторы базиса выбрать взаимно перпендикулярными и имеющими единичную длину, то такая АСК на плоскости носит название декартовой прямоугольной системой координат (ДПСК). Базисные вектора, входящие в ДПСК обозначают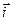 
и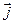 
(кратчайший поворот против часовой стрелки от 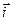к ).
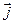На плоскости существуют и другие системы координат. Задавая на плоскости некоторую АСК, мы устанавливаем взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел.
п. 3 Базис в пространстве
Определение 1. Векторы 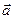, , называются компланарными, если они лежат на одной или параллельных плоскостях.
Определение 2. Базисом в пространстве называется упорядоченная тройка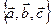 
произвольных некомпланарных векторов. АСК в пространстве называется совокупность фиксированной точки 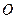и некоторого базиса 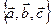, приведённого к этой точке.
Теорема1. Пусть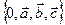 
некоторая АСК в пространстве. Тогда любой вектор 
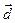можно представить в виде 
, 
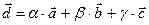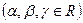и притом единственным образом.
Доказательство:
Совместим начало вектора 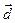с началом координат точкой 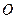. Проведем через конец вектора 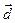две прямые:
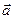§ первую параллельно вектору до пересечения с плоскостью, в которой лежат и ;
§ вторую параллельно плоскости, в которой лежат 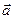и , до пересечения с прямой, на которой лежит вектор .
Тогда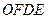 
– параллелограмм, следовательно, 
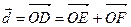. Вектор 
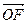лежит на плоскости, образованной векторам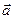и и . По теореме о разложении по базису на плоскости имеем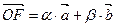 
.
Вектор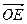 
коллинеарен вектору , следовательно, 
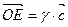. Таким образом .
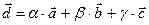Нетрудно показать единственность разложения. ■
Пример. Дано: Векторы 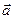, и некомпланарны.
Доказать: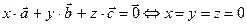 
.
Доказательство:
Если хотя бы одно из чисел в равенстве, например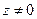 
, то равенство 
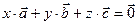эквивалентно равенству 
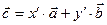, где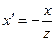 
, 
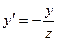, что означает компланарность векторов 
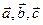. Получили противоречие условию. Следовательно, 
.
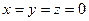Обратно: если 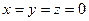, то равенство 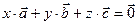очевидно. ■
п. 4 Линейная независимость векторов
Определение 1. Пусть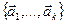 
– система векторов в пространстве, где 
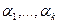– вещественные числа. Тогда вектор 
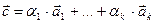называется линейной комбинацией векторов 
,…, 
.
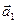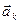Определение 2. Система векторов 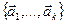называется линейно зависимой, если хотя бы один из векторов данной системы является линейной комбинацией остальных векторов.
Определение 3. Система векторов 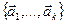называется линейно независимой, если ни один из векторов данной системы не является линейной комбинацией остальных векторов.