Тема: Формула суммы n первых членов геометрической прогрессии

Дата: 2025-06-14; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

9 класс Алгебра 15.03.2023

Тема: Формула суммы n первых членов геометрической прогрессии

Цель урока: формирование знаний и первичное закрепление умений по теме «Формула суммы n первых членов геометрической прогрессии»

Ход урока

1.Постановка целей урока
Сегодня, ребята, мы продолжаем изучение геометрической прогрессии. Запишем тему урока в тетради: «Сумма n первых членов геометрической прогрессии». Мы должны познакомиться с формулой суммы первых п членов геометрической прогрессии и учиться применять ее.

2.Устная работа
Вопросы
1. Какая последовательность называется арифметической прогрессией? 2. Какая последовательность называется геометрической прогрессией?

3. В третьем тысячелетии високосными годами будут 2008, 2012 ,2016, 2020 продолжите, в какой последовательности записаны года?

· Формула n-го члена арифметической прогрессии.

· Формула n-го члена геометрической прогрессии.

• Формула суммы n-первых членов арифметической прогрессии
• Формула для нахождения разности арифметической прогрессии
• Формула для нахождения знаменателя геометрической прогрессии

3. Историческая справка
Индийский царь Шерам, впервые познакомившись с шахматами, восхитился их своеобразием и обилием красивых комбинаций. Узнав, что замечательную игру изобрёл его подданный Сета, царь призвал к себе мудреца, желая лично наградить за выдумку. Властелин обещал выполнить любую его просьбу и был удивлен, когда тот попросил лишь некоторое количество пшеничных зёрен. На первое поле доски он попросил положить одно зерно, на второе – два и так далее: на каждое последующее поле нужно было класть вдвое больше зерен, чем на предыдущее. Царь распорядился побыстрее выдать изобретателю его ничтожную награду. Однако на следующий день придворные математики сообщили своему повелителю, что для выполнения его приказа не хватит пшеницы, хранящейся не только в амбарах всего царства, но и во всех амбарах мира. Мудрец скромно потребовал

1 + 2 + 2² + … + 2⁶³ = 2⁶⁴ - 1 зерно. Это число записывается двадцатью цифрами и фантастически велико.

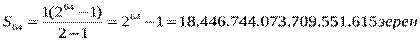
18 квинтиллионов 446 квадриллионов
744 триллиона 73 миллиарда
709 миллионов 551 тысяча 615 зерен

4. Изучение нового материала

Пусть дана геометрическая прогрессия (bn ). Обозначим сумму п первых её членов через S_n:

S_n=b₁+b₂+b₃+…+b_n-1+b_n. (1)

Умножим обе части этого равенства на q:

S_nq=b₁q+b₂q+b₃q+…+b_n-1q+b_nq.

Учитывая, что b₁q=b₂, b₂q=b₃, b₃q=b₄, …, b_n-1q=b_n,

Получим S_nq =b₂+b₃+b₄+…+b_n+b_nq. (2)

Вычтем почленно из равенства (2) равенство (1) и приведём подобные члены:

S_nq – S_n=( b₂+b₃+…+b_n+b_nq) – (b₁+b₂+…+b_n-1+b_n)=b_nq – b₁.

S_n (q – 1)=b_nq – b₁.

Отсюда следует, что при q ≠ 1
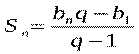. (I)

Мы получили формулу суммы п первых членов геометрической прогрессии, в которой q ≠ 1. Если q=1, то все члены прогрессии равны первому члену и

S_n =nb₁.

При решении многих задач удобно пользоваться формулой суммы п первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (I) вместо b_n выражение b₁q^{n – 1}. Получим:

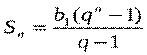, если q ≠ 1. (II)

5. Решение задач. № 648 (а), 650(а), 653 (а), 652 (а)

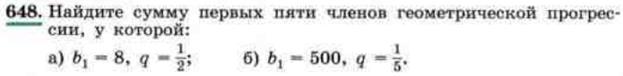
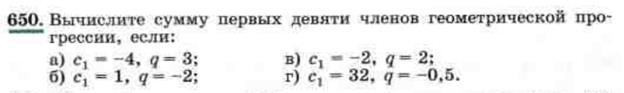
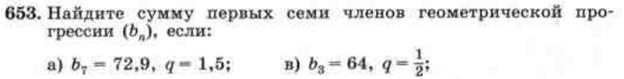
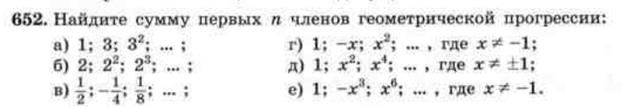
6. Домашнее задание.

П. 28 стр. 168-170 выучить формулы, выполнить №649 (а, б), 654