Решение общих задач линейного программирования

Дата: 2025-06-02; Просмотры: 10

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

ДЕПАРТАМЕНТ КАДРОВОЙ ПОЛИТИКИ И ОБРАЗОВАНИЯ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПО ЗЕМЛЕУСТРОЙСТВУ

КАФЕДРА ЗЕМЛЕУСТРОЙСТВА

С.Н. Волков, В.В. Бугаевская, А.В. Купчиненко

ЭКОНОМИКО–МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ

СИМПЛЕКСНЫЙ МЕТОД

Задания для выполнения расчётно–графических, лаборат орных,

самостоятельных и контрольных работ

Для студентов высших учебных заведений по специальностям:

310900 – Землеустройство

311000 – Земельный кадастр

311100 – Городской кадастр

и направлению:

560600 –Землеустройство и земельный кадастр

Москва 2003

УДК 332.3:519.86

Подготовлены к печати кафедрой землеустройства Государственного университета по землеустройству (протокол № 13 от 22 мая 2003 года).

Рекомендованы учебно-методическим объединением по образованию в области землеустройства и кадастров в качестве лабораторных, расчетно-графических, самостоятельных и контрольных работ по дисциплине экономико-математические методы и моделирование для межвузовского использования (протокол № 3 от 7 июня 2003 г.).

Составители: д.э.н, профессор С.Н. Волков;

к.э.н., доцент В.В. Бугаевская

к.э.н., профессор А.В. Купчиненко.

Рецензенты: к.э.н., доцент В.И. Нилиповский

(кафедра экономической теории и менеджмента ГУЗ);

д.т.н., проф. А.Н. Безгинов

(кафедра землеустройства ГУЗ)

ЗАДАНИЕ II

СИМПЛЕКС – МЕТОД

РЕШЕНИЕ ОБЩИХ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Решить задачу линейного программирования вручную.

Демонстрационная задача 1. Определить целесообразное сочетание отраслей сельскохозяйственного производства, обеспечивающего максимум стоимости товарной продукции. Ресурсы хозяйства, а также нормативные показатели отраслей приведены в табл. 1.

С 1га кормовых угодий выход корма принять 10 ц к.е.

Таблица 1

Исходные данные к задаче

№ п/п	Показатели	Ед. изм.	Нормативные показатели отраслей				Ресурсы хозяйства
			Зерновые		Кормовые	Поголовье коров
			Продовольственные	Фуражные
			га	га	га	гол.
			Х1	Х2	Х3	Х4
1.	Пл. пашни	га	1	1	1		3300*
2.	Пл. сенокосов и пастбищ	га					400*
3.	Затраты труда	чел. час.	42**	35**	80**	120**	250000*
4.	Урожайность	Ц к.е.	30	30	38**
5.	Нормы кормления	Ц к.е.				54
6.	Стоимость товарной продукции	тыс. руб.	4.2			30

Порядок выполнения задачи.

1. Описание основных переменных:

х₁ – площадь зерновых продовольственных, га

х₂ – площадь зерновых фуражных, га

х₃ – площадь кормовых культур, га

х₄ – поголовье коров, гол.

2. Целевая функция: Максимум стоимости товарной продукции, тыс. руб. При формировании целевой функции необходимо учесть урожайность зерновых продовольственных культур, продуктивность коров и цены на продукцию:

4,2х₁ + 30х₄ 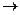max

3. Система ограничений:

3.1. Ограничение по использованию площади пашни, га:

х₁ + х₂ + х₃ 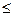3300;

3.2. Ограничение по использованию трудовых ресурсов, чел. час.:

42х₁ + 35х₂ + 80х₃ + 120х₄ 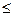250000;

3.3. Ограничению по производству и потреблению кормов, ц к.е.

Составим ограничение по балансу кормов, исходя из того, что потребление корма должно быть меньше его производства. При построении ограничений необходимо помнить, что в окончательной записи ограничения преобразуются к стандартной форме: все неизвестные с коэффициентами должны находиться в левой части ограничения и располагаться по возрастанию индексов переменных, а в правой части ограничения стоит значение константы (ресурса), а при его отсутствии - ноль. При составлении ограничения учитываются нормы кормления и поголовье животных, урожайность и площади посева кормовых культур, а также питательность различных видов кормов:

-30х₂ - 38х₃ + 54х₄ 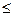4000

4. Составим экономико-математическую модель задачи (табл. 2).

Таблица 2

Экономико-математическая модель задачи

№ п.п	Вид ограничения	Коэффициенты при основных переменных				Тип огр.	Правые части огр.
		Х1	Х2	Х3	Х4
1.	Общая пл. пашни	1	1	1		<=	3300*
2.	Трудовые затраты	42**	35**	80**	120**	<=	250000*
3.	Баланс кормов		-30	-38	54	<=	4000*
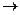
Z	Стоимость товарной продукции	4.2	0	0 30			max

5. Каноническая форма записи задачи:

х₁ + х₂ + х₃ + х₅ = 3300

42х₁ + 35х₂ + 80х₃ + 120х₄ +х₆ = 250000

- 30х₂ - 38х₃ + 54х₄ + х₇ = 4000

4,2х₁ + 0*х₂ + 0*х₃ + 30х₄+0*х₅+0*х₆ + 0*х₇ 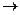max

6. Описание дополнительных переменных:

х₅ – недоиспользованная площадь пашни, га

х₆ – недоиспользованный труд, чел. час

х₇ – недоиспользованные корма, ц к.е.

7. Запись математической формулировки задачи в структурном виде.

Введем следующие обозначения:

Х_j(j 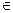Q₁) – площади посевов сельскохозяйственных культур;

Q₁ – множество площадей посевов сельскохозяйственных культур;

х_j (j 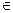Q₂) – поголовье скота;

Q₂ – множество видов и групп скота.

1). По использованию площади пашни, га:

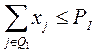, где i 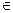M_1, M₁ – множество видов пашни;

2). По использованию трудовых ресурсов, чел. час.:

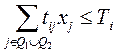, где i 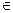M_2, M₂ – множество видов труда;

t_ij – норма затрат i-го вида труда на единицу j-ой отрасли (на 1га посева сельскохозяйственной культуры или на 1 голову скота);

3). Баланс кормов:

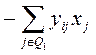
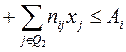; где i 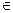M_3, М₃ – множество видов кормов;

y_ij – выход i-го вида корма с 1га j-ой кормовой культуры;

n_ij – норма кормления i-ым видом корма j-го вида скота;

Целевая функция:

Z = 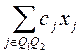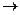max, где c_j – стоимость товарной продукции, получаемой с единицы отрасли.

8. Опорное решение задачи определяется следующим образом: все основные и избыточные переменные приравниваются нулю, а остаточные и искусственные приравниваются правым частям ограничений. Дальнейший процесс решения задачи проводят в симплексных таблицах.

Первая симплексная таблица соответствует первому опорному решению (табл. 3).

Первая строка таблицы содержит коэффициенты при неизвестных в каноническом представлении целевой функции;

первый столбец – нумерация ограничений;

второй столбец содержит набор базисных переменных;

третий столбец – номер ограничения для дополнительной переменной;

четвёртый столбец – оценка целевой функции: оценка целевой функции равна соответствующим коэффициентам при базисных переменных целевой функции в каноническом представлении;

Таблица 3

Первая симплексная таблица

	№ п/п	Баз. пер.	№ ограничения для доп. пер.	СI Оценка целевой функции	Аio значение базисной переменной	Сj	4,2	0	0		30		0	0	0		Конт	Част. от дел.
							Коэффициенты замещения
							х1	х2		х3		х4	х5 (ост. в огр. 1)	х6 (ост. в огр. 2)	х7 (ост. в огр. 3)
1.		х5	(1)	0	3300		1	1		1			1			3304		-
2.		х6	(2)	0	250000		42	35		80		120		1		250278		2083,3
3.		х7	(3)	0	4000			-30		-38		54			1	3987		74,1
4.		Zj-Cj			0		-4,2	0		0		-30	0	0	0	-34,2		-

пятый столбец – значения базисных переменных (A_io). Столбец свободных членов формируется из правых частей исходной системы ограничений;

В качестве коэффициентов замещения берутся соответствующие коэффициенты при переменных системы ограничений в канонической форме.

В столбце сумма находится сумма значений всех коэффициентов, начиная со столбца свободных членов.

Элементы индексной строки вычисляются по формуле:

(Z_j – C_j,) = 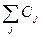^. A_io - C_j, j=0, 1,2,…7, где C_j, j=0, 1,2,…7 – коэффициенты при соответствующих переменных целевой функции в каноническом виде.

Построение второй симплекс – таблицы.

Шаг 1. Определение переменной, вводимой в базис. При решении задачи на максимум это будет переменная, в индексной строке которой находится максимальный по абсолютной величине отрицательный элемент. Вводимой в базис переменной будет переменная Х_4. Данный столбец называется ключевым.

Шаг 2. Определение выводимой из базиса переменной. Базисная переменная, находящаяся в строке, в которой результат поочередного деления значений элементов столбца свободных членов на соответствующие положительные элементы ключевого столбца оказался минимальным, будет выводиться из базиса. Результаты деления записываются в последнем столбце симплекс-таблицы. Они показывают, что минимальное частное находится в строке с базисной переменной Х_7.

Эта строка называется ключевой. Элемент, который находится на пересечении ключевого столбца и ключевой строки называется ключевым.

Шаг 3. Во второй симплексной таблице из базиса исключается переменная Х₇ и на ее место ставится переменная Х₄. Эта строка называется начальной.

Шаг 4. Проверка на оптимальность. Если в индексной строке находятся отрицательные элементы, то решение необходимо улучшать. При решении на максимум признаком оптимальности является неотрицательность элементов индексной строки.

Шаг 5. Расчет элементов начальной строки производится путем деления соответствующих коэффициентов ключевой строки на ключевой элемент.

Все остальные элементы второй симплекс-таблицы, включая элементы индексной строки и столбца сумма 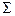рассчитываются по формуле:

,

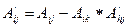где 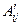- элемент следующей симплекс – таблицы;

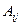- элемент предыдущей симплекс – таблицы;

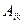- элемент преобразуемой i-ой строки, расположенного в ключевом столбце;

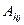- элемент, начальной строки (j – го столбца).

Столбец контроль считается как сумма всех элементов, начиная со столбца свободных членов и до столбца последней переменной.

9. Контроль вычислений.

Для контроля вычислений необходимо следить за тем, чтобы:

- сходились пять значащих цифр в значениях соответствующих элементов в столбце сумма и в столбце контроль;

- значение целевой функции при переходе от итерации к итерации должно увеличиваться при решении на максимум.

Выполнить итоговый контроль решения:

- в уравнения канонической формы подставить найденные значения неизвестных и проверить соблюдаются ли равенства;

- произвести контроль решения по формуле:

=

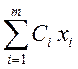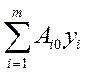
где х_i – значения базисных переменных (элементы столбца A_i0 последней симплексной таблицы);

C_i – коэффициенты целевой функции при базисных переменных;

A_i0 – свободные члены исходной системы условий (элементы столбца исходной симплексной таблицы )

y_i – двойственные переменные, находящиеся в индексной строке в столбцах дополнительных переменных, соответствующих i-му уравнению.