Рис. 5. Траектория полета шарика при стрельбе горизонтально
Теперь рассмотрим движение под углами α равными π/4, π/3 и π/6. При этом есть фаза подъема, которая заканчивается при vy=0. Масса тела и коэффициенты сопротивления среды берем такие же, как в предыдущем случае. Задаем начальный угол =ПИ()/4. И рассчитываем начальные скорости по горизонтали и вертикали. Горизонтальная скорость и дальность рассчитывается как и в предыдущем случае. Вертикальная скорость вначале уменьшается, а высота растет. После достижения максимального подъема формулы корректируем: скорость будет расти, а высота уменьшаться. Потому в выделенных ячейках формулы изменяются согласно (17) для вертикальной скорости и для высоты по (18). В таблице 9 приведены часть расчетных формул, данные полностью приведены в приложении 3.
Таблица 9.
Формулы для моделирования движения тела под углом к горизонту при α=π/4
| 32 | v_0= | 50 | m/s | a= | =ПИ()/4 | |
| 33 | v_0x= | =B28*COS(F28) | м/с | tg(a)= | =B30/B29 | |
| 34 | v_0y= | =B28*SIN(F28) | м/с | |||
| 35 | ||||||
| 36 | t | v_x | v_y | H | L | |
| 37 | 0 | =B29 | =B30 | 0 | 0 | |
| 38 | 0,1 | =B33-(L$8*B33+L$9*B33*B33)/ H$6*(A34-A33) | =C33+(-H$6*B$6-L$8*C33-L$9*C33*C33)/H$6*(A34-A33) | =D33+C33*(A34-A33) | =E33+B33*(A34-A33) | подъем |
| 39 | 0,2 | =B34-(L$8*B34+L$9*B34*B34)/ H$6*(A35-A34) | =C34+(-H$6*B$6-L$8*C34-L$9*C34*C34)/H$6*(A35-A34) | =D34+C34*(A35-A34) | =E34+B34*(A35-A34) | |
| 63 | 3 | =B62-(L$8*B62+L$9*B62*B62)/ H$6*(A63-A62) | =C62+(-H$6*B$6-L$8*C62-L$9*C62*C62)/H$6*(A63-A62) | =D62+C62*(A63-A62) | =E62+B62*(A63-A62) | максимальный подъем |
| 64 | 3,1 | =B63-(L$8*B63+L$9*B63*B63)/ H$6*(A64-A63) | =C63+(H$6*B$6-L$8*C63-L$9*C63*C63)/H$6*(A64-A63) | =D63-C63*(A64-A63) | =E63+B63*(A64-A63) | начало падения |
| 65 | 3,2 | =B64-(L$8*B64+L$9*B64*B64)/ H$6*(A65-A64) | =C64+(H$6*B$6-L$8*C64-L$9*C64*C64)/H$6*(A65-A64) | =D64-C64*(A65-A64) | =E64+B64*(A65-A64) | |
| 66 | 3,3 | =B65-(L$8*B65+L$9*B65*B65)/ H$6*(A66-A65) | =C65+(H$6*B$6-L$8*C65-L$9*C65*C65)/H$6*(A66-A65) | =D65-C65*(A66-A65) | =E65+B65*(A66-A65) |
Траектория движения тела показана на следующем рисунке.
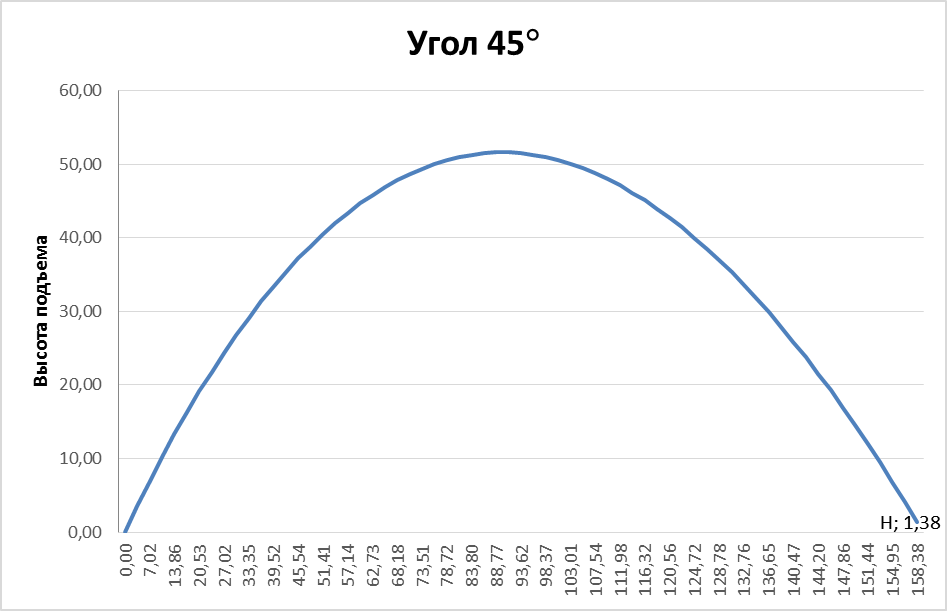
Рис. 6. Траектория полета шарика при стрельбе под углом к горизонту при α=π/4
Таким же способом производятся расчеты при значениях углов π/3 и π/6. Полученные таблицы данных приведены в приложении 3. Здесь приведем только рисунки полученных траекторий движения тела.
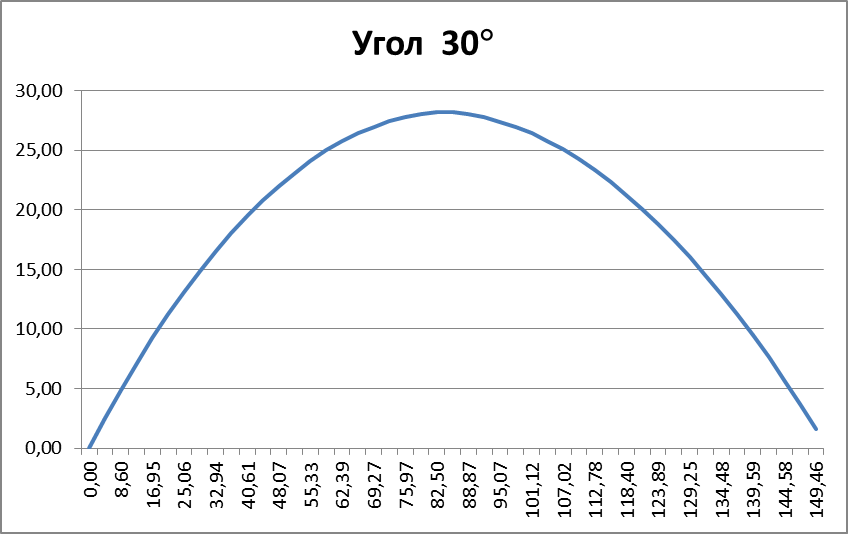
Рис. 7. Траектория полета шарика при стрельбе под углом к горизонту при α=π/6
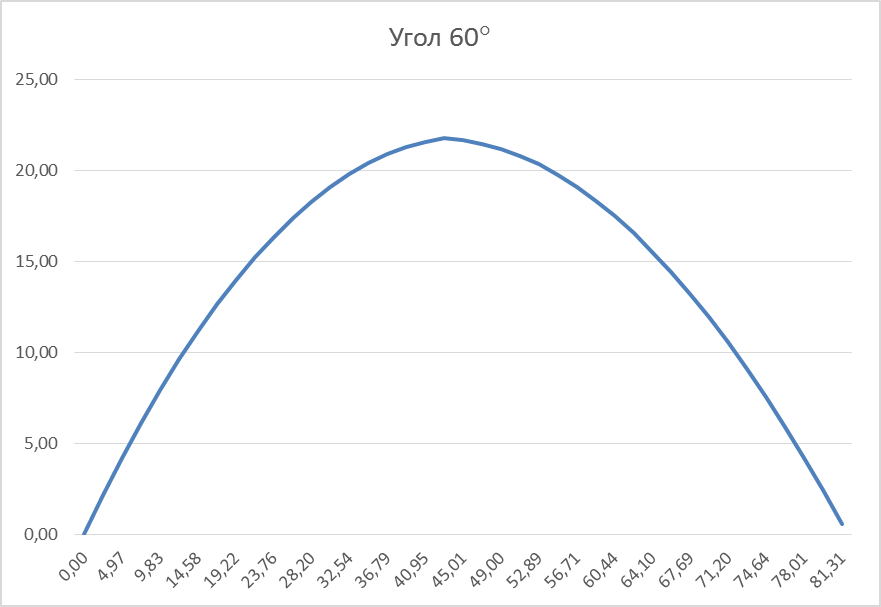
Рис. 8. Траектория полета шарика при стрельбе под углом к горизонту при α=π/3
Из рисунков видно, что максимальная высота подъема и дальность полета наблюдается при стрельбе под углом α=π/4.
Сравним результаты моделирования дальности полета тела и максимальной высоты подъема с теоретическими значениями, получаемыми по формулам:
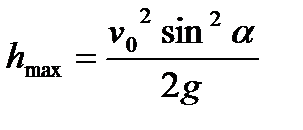
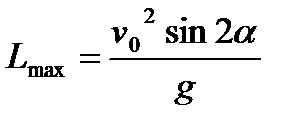
При стрельбе горизонтально дальность рассчитывается по другой формуле:
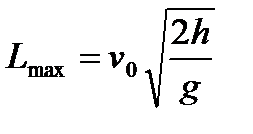
Таблица 10.
Сравнение результатов моделирования дальности полета тела и максимальной высоты подъема с теоретическими значениями
|
| углы | |||
|
| 45° | 30° | 60° | 0° |
| дальность | ||||
| теоретическое значение | 255,10 | 220,92 | 220,92 | 27,66 |
| результаты моделирования | 158,38 | 149,46 | 81,31 | 26,45 |
| относительное отклонение | 37,91% | 32,35% | 63,20% | 4,37% |
| высота подъема | ||||
| теоретическое значение | 65,28 | 33,39 | 97,16 |
|
| результаты моделирования | 51,57 | 28,17 | 21,69 |
|
| относительное отклонение | 20,99% | 15,63% | 77,68% |
|
Из таблицы видно, что и максимальная высота подъема тела, и дальность полета, полученная в результате моделирования, меньше теоретических значений. Причем отклонение тем больше, чем больше начальный угол. Это вполне согласуется с практическими данными
Заключение
Будущее тесно связано с цифровыми технологиями. Компьютерное моделирование смело вошло в нашу жизнь. Оно пронизывает все области жизнедеятельности. От подобного развития уже никуда не деться. Человечество в своей деятельности (научной, образовательной, технологической, художественной) постоянно создает и использует модели окружающего мира. Модели позволяют представить в наглядной форме объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, очень быстрые или очень медленные). Модели играют чрезвычайно важную роль в проектировании и создании различных технических устройств, машин и механизмов, зданий, электрических цепей и т. д. Развитие науки невозможно без создания теоретических моделей (теорий, законов, гипотез и пр.), отражающих строение, свойства и поведение реальных объектов. Все художественное творчество фактически является процессом создания моделей. Более того, практически любое литературное произведение может рассматриваться как модель реальной человеческой жизни. Моделями в художественной форме отражающими реальную действительность, являются также живописные полотна, скульптуры, театральные постановки и пр. Моделирование — это метод познания. А познавая мир, человечество движется вперед, развивается. В этом и заключается жизнь.
В своей работе мы рассмотрели понятие и классификацию моделей и их основные свойства, особенности компьютерного моделирования. Во второй части работы мы изучили вопросы, связанные с описанием движения тела с учетом сопротивления среды. Получили математическую модель свободного падения тела и движения тела под углом к горизонту. В третьей части мы выполнили практические расчеты по полученным моделям в табличном процессоре MS Excel и визуализировали результаты в виде графиков.
Таким образом, поставленные нами в работе задачи решены, цель работы достигнута.
По теме работы опубликована статья «Построение модели движения тела с учетом сопротивления среды в таблице MS Excel» в сборнике Студенческая наука: гипотезы и аппробации. Выпуск 11 (Брянск, 2021, с.286-291).
Литература
1. Могилев, А.В. Информатика: Учебное пособие для студентов высших педагогических учебных заведений/А.В. Могилев, Е.К. Хеннер, Н.И. Пак; под ред. А.В. Могилева. – 3-е изд., стер. – М.: Академия, 2015. – 336с.
2. Михеева, Е.В. Практикум по информационным технологиям в профессиональной деятельности: Учебное пособие для среднего профессионального образования/Е.В. Михеева – М.: Академия, 2005 – 256с.
3. Боев, В.Д. Компьютерное моделирование: курс / В.Д. Боев, Р.П. Сыпченко. – Москва : Интернет-Университет Информационных Технологий (ИНТУИТ), 2010. – 455 с. : ил.,табл., схем. – Режим доступа: по подписке. – URL: https://biblioclub.ru/index.php?page=book&id=233705 (дата обращения: 14.03.2021). – Текст : электронный.
4. Белошапка В К Информационное моделирование в примерах и задачах. -Омск: Из-во ОГПИ, 1992.








