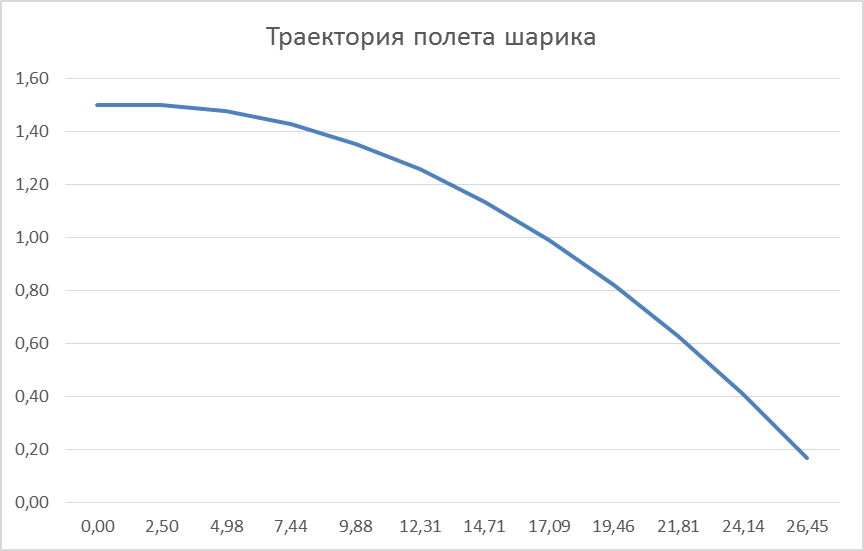
Рис. 3. График изменения высоты и скорости движения при падении тела в воде
Результаты построения модели движения каплевидного тела в воде приведены в приложении 2. При проведении расчетов учтено, что как и при падении в воздухе, коэффициент лобового сопротивления для капли с=0,045 и площадь поперечного сечения уменьшается при вытягивании «хвостика» капли. Чем более вытянутой является капля, тем меньше сопротивление воздуха и выше скорость падения. На рис. 4 представлен график разности скоростей для капель одинаковой массы, но с разным поперечным сечением. Движение обоих тел быстро становится равномерным. Но более вытянутое падает быстрее.
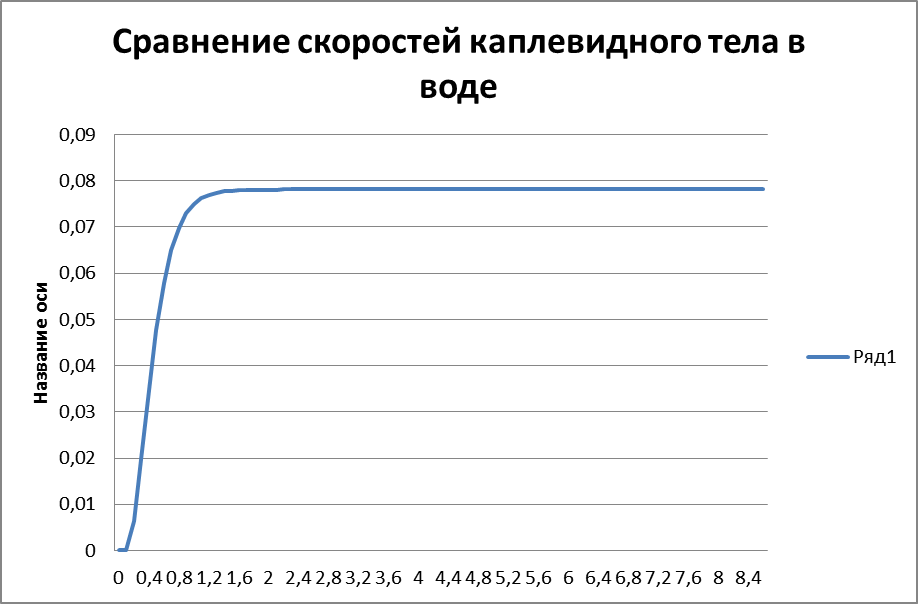
Рис. 4. Зависимость разности скоростей каплевидных тел разного сечения при падении в воде.
3.3. Построение модели полета свинцового шарика под углом к горизонту с учетом сопротивления воздуха
Решим задачу 3. Будем считать, что свинцовый шарик (такой же, как в задаче 1) вылетает из рогатки, находящейся на высоте 1,5м со скоростью 50 м/с под заданным углом. При вычислениях нужно учитывать горизонтальную и вертикальную составляющие скорости, которые вычисляются по формулам (13), (15) и (17) независимо друг от друга, а также дальность и высоту полета (формулы (14), (16) и (18)). Переход между формулами (15) и (17), (16) и (18) определяется сменой направления движения по вертикали: при стрельбе вверх тело сначала поднимается, а затем, когда вертикальная скорость станет равной 0, начнется спуск. Это условие нужно учитывать при копировании формул в таблице.
Проведем расчеты для разных начальных углов.
При α=0 фаза подъема при движении отсутствует. Масса тела и коэффициенты сопротивления среды берем такие же, как в задаче 1. В строке 12 задаем начальные значения горизонтальной и вертикальной составляющей скорости, высоты и дальности. В столбце А задаем время с выбранным шагом. В ячейки В13, С13 задаем формулы для вычисления скорости согласно (13) и (17), высоту и дальность рассчитываем по формулам (18) и (14). Ссылки на ячейки с параметрами задаем в смешанной форме, чтобы они не изменялись при копировании. Затем выделяем диапазон B13:L13 и протягиваем выделение до тех пор, пока значение высоты остается положительным.
Таблица 8.
Формулы для моделирования движения тела под углом к горизонту при α=0
| A | B | C | D | E | |
| 11 | t | v_x | v_y | H | L |
| 12 | 0 | 50 | 0 | 1,5 | 0 |
| 13 | 0,05 | =B12-(L$8*B12+L$9*B12*B12)/H$6*(A13-A12) | =C12+(H$6*B$6-L$8*C12-L$9*C12*C12)/H$6*(A13-A12) | =D12-C12*(A13-A12) | =E12+B12*(A13-A12) |
| 14 | 0,1 | =B13-(L$8*B13+L$9*B13*B13)/H$6*(A14-A13) | =C13+(H$6*B$6-L$8*C13-L$9*C13*C13)/H$6*(A14-A13) | =D13-C13*(A14-A13) | =E13+B13*(A14-A13) |
| 15 | 0,15 | =B14-(L$8*B14+L$9*B14*B14)/H$6*(A15-A14) | =C14+(H$6*B$6-L$8*C14-L$9*C14*C14)/H$6*(A15-A14) | =D14-C14*(A15-A14) | =E14+B14*(A15-A14) |
| 16 | 0,2 | =B15-(L$8*B15+L$9*B15*B15)/H$6*(A16-A15) | =C15+(H$6*B$6-L$8*C15-L$9*C15*C15)/H$6*(A16-A15) | =D15-C15*(A16-A15) | =E15+B15*(A16-A15) |
| 17 | 0,25 | =B16-(L$8*B16+L$9*B16*B16)/H$6*(A17-A16) | =C16+(H$6*B$6-L$8*C16-L$9*C16*C16)/H$6*(A17-A16) | =D16-C16*(A17-A16) | =E16+B16*(A17-A16) |
| 18 | 0,3 | =B17-(L$8*B17+L$9*B17*B17)/H$6*(A18-A17) | =C17+(H$6*B$6-L$8*C17-L$9*C17*C17)/H$6*(A18-A17) | =D17-C17*(A18-A17) | =E17+B17*(A18-A17) |
| 19 | 0,35 | =B18-(L$8*B18+L$9*B18*B18)/H$6*(A19-A18) | =C18+(H$6*B$6-L$8*C18-L$9*C18*C18)/H$6*(A19-A18) | =D18-C18*(A19-A18) | =E18+B18*(A19-A18) |
| 20 | 0,4 | =B19-(L$8*B19+L$9*B19*B19)/H$6*(A20-A19) | =C19+(H$6*B$6-L$8*C19-L$9*C19*C19)/H$6*(A20-A19) | =D19-C19*(A20-A19) | =E19+B19*(A20-A19) |
| 21 | 0,45 | =B20-(L$8*B20+L$9*B20*B20)/H$6*(A21-A20) | =C20+(H$6*B$6-L$8*C20-L$9*C20*C20)/H$6*(A21-A20) | =D20-C20*(A21-A20) | =E20+B20*(A21-A20) |
| 22 | 0,5 | =B21-(L$8*B21+L$9*B21*B21)/H$6*(A22-A21) | =C21+(H$6*B$6-L$8*C21-L$9*C21*C21)/H$6*(A22-A21) | =D21-C21*(A22-A21) | =E21+B21*(A22-A21) |
| 23 | 0,55 | =B22-(L$8*B22+L$9*B22*B22)/H$6*(A23-A22) | =C22+(H$6*B$6-L$8*C22-L$9*C22*C22)/H$6*(A23-A22) | =D22-C22*(A23-A22) | =E22+B22*(A23-A22) |
Таблица полученных значений приведена в приложении 3. На рис. 5 видно, что траектория полета близка к параболе, т.е. при таких начальных условиях торможение из-за сопротивления воздуха заметно слабо.