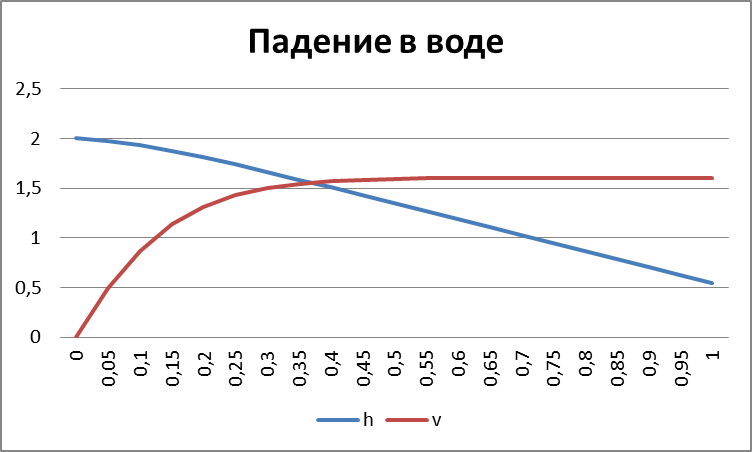
Рис. 1. График изменения высоты и скорости движения при свободном падении тела в воздухе

Дата: 2025-06-02; Просмотры: 13
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Результаты построения модели движения каплевидного тела в аналогичных условиях приведены в приложении 2. При проведении расчетов учтено, что коэффициент лобового сопротивления для капли с=0,045 и площадь поперечного сечения уменьшается при вытягивании «хвостика» капли. Чем более вытянутой является капля, тем меньше сопротивление воздуха и выше скорость падения. На рис. 2 представлен график разности скоростей для капель одинаковой массы, но с разным поперечным сечением.

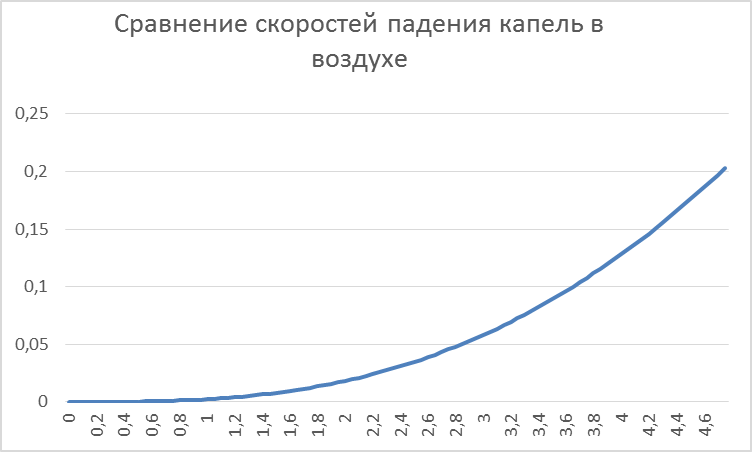
Рис. 2. Зависимость разности скоростей падающих капель разного сечения при свободном падении в воздухе

 

 

3.2. Построение модели падения свинцового шарика в воде с учетом сопротивления среды

 

Решим в MS Excel задачу 2 п. 2.3 на том же рабочем листе, что и задачу 1. Характеристики шарика заданы в таблице 1. Для расчета требуются плотность и динамическая вязкость воды (справочные данные) и значения коэффициентов сопротивления, вычисленные в задаче 2:

Таблица 5.

Плотность и динамическая вязкость воды, коэффициенты сопротивления

 

F

G

H
6

вода
7

μ=

1,002

Нс/м^2
8

ρ_=

1000

кг/м^3
9

k1=

0,1889

Нс/м
10

k2=

0,0628

кг c/м

 

Так как падение в воде происходит медленнее, то начальную высоту зададим 2м и завершим вычисления, когда движение станет равномерным (изменение скорости составляет менее 0,0001 за один шаг вычислений). Проведем расчеты скорости и высоты тела по формулам (9) и (10) аналогично задаче 1 (см. таблицу 6). Для проведения расчетов дальше нужно выделить диапазон ячеек G14:H14 и протянуть выделение вниз для копирования формул (как и в предыдущей задаче). Завершить протягивание нужно при появлении в столбце I надписи «торможение». Приведем в таблице 6 часть расчетных формул, а в таблице 7 – вычисленные значения. Полностью результаты расчетов для этой задачи приведены в приложении 1.

 

Таблица 6.

Формулы для расчета высоты и скорости падения в воде

 

F

G

H

I
12

t

h

v
13

0

=$B3

=G4
14

0,1

=G13-H14*(F14-F13)

=H13+($H$2*$B$2-G$9*H13-G$10*H13*H13)/$H$2*(F14-F13)

=ЕСЛИ(H14-H13<=0,0001; "торможение";""
15

0,2

=G14-H15*(F15-F14)

=H14+($H$2*$B$2-G$9*H14-G$10*H14*H14)/$H$2*(F15-F14)

=ЕСЛИ(H15-H14<=0,0001; "торможение";""

 

Таблица 7.

Расчет высоты и скорости падения в воде

 

F

G

H

I
12

t

h

v
13

0

2

0
14

0,05

1,976

0,490
15

0,1

1,932

0,867
16

0,15

1,875

1,135
17

0,2

1,810

1,314
18

0,25

1,738

1,429
19

0,3

1,663

1,500
20

0,35

1,586

1,543
21

0,4

1,508

1,569
22

0,45

1,429

1,584
23

0,5

1,349

1,593
24

0,55

1,269

1,599
25

0,6

1,189

1,602
26

0,65

1,109

1,604
27

0,7

1,028

1,605
28

0,75

0,948

1,605
29

0,8

0,868

1,606
30

0,85

0,788

1,606
31

0,9

0,707

1,606
32

0,95

0,627

1,606

торможение
33

1

0,547

1,606

торможение

 

Результаты проведения расчетов представим графически. Для этого вставим на рабочий лист диаграмму (график) для рядов данных G12:G33 (высота тела) и H12:H33 (скорость падения), в качестве подписей по оси OX используем значения времени из диапазона F12:F33. Результаты представлены на рис. 3. Из рисунка видно, что скорость погружения сначала возрастает, затем изменение скорости замедляется и движение становится практически равномерным. Изменение высоты тела при этом быстро становится линейным.