2. Математическая модель движения тела с учетом сопротивления среды
При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Предмет, сброшенный с большой высоты, вовсе не движется равноускорено, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту, относительно несложную, задачу нельзя решить средствами «школьной» физики; и таких задач, представляющих практический интерес, очень много. Прежде чем приступать к построению соответствующих моделей, вспомним, что известно о силе сопротивления.
О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (и зависит от среды). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение Fcoпp = k 1 v , где k 1 определяется свойствами среды и формой тела. Например, для шарика k 1= 6πμr - это формула Стокса, где μ-динамическая вязкость среды, r - радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм.μ = 0,0182 Н∙с∙м-2, для воды 1,002 Н∙с∙м-2, для глицерина 1480 Н∙с∙м-2.
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (и движение станет равномерным).
Имеем 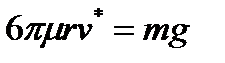 , или
, или 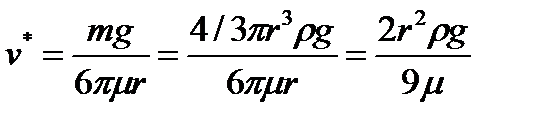 .
.
Пусть r = 0,1 м, ρ = 0,8∙103 кг/м3 (дерево). При падении в воздухе v * ≈ 960 м/с, в воде v*≈ 17 м/с, в глицерине v * ≈ 0,012 м/с.
На самом деле эти результаты совершенно не соответствуют действительности (и дерево в воде и глицерине тонуть не будет).
Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: Fcoпp=k 2 v 2 . Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если k2v2>>k 1 v , то вкладом k 1 v можно пренебречь (это конкретный пример ранжирования факторов). О величине k 2 известно следующее: она пропорциональна площади сечения тела S , поперечного по отношению к потоку, и плотности среды ρсреды и зависит от формы тела. Обычно представляют k 2 = 0,5сSρсрeды, где с - коэффициент лобового сопротивления - безразмерен. Значения с берут из соответствующих 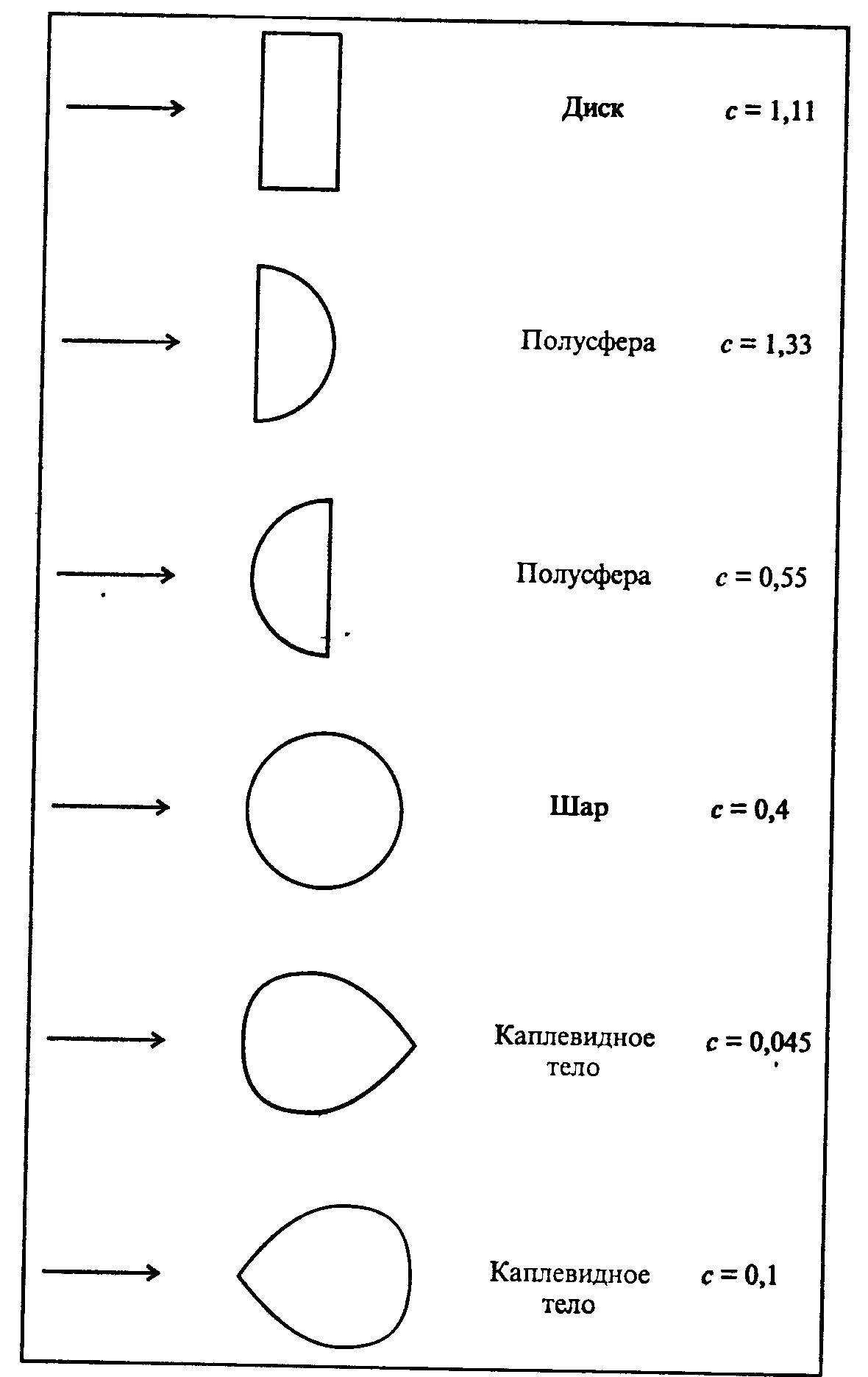
справочников (см. рис. 1)
Рисунок 1. Зависимость коэффициента лобового сопротивления от формы тела
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение в несколько раз уменьшается; для шара оно становится приблизительно равным 0,1.
Вернемся к указанной выше оценке, исходя из квадратичной зависимости силы сопротивления от скорости.
Имеем 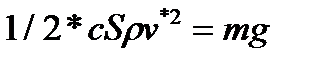 или
или 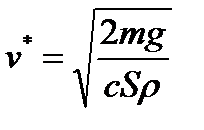
Для шарика 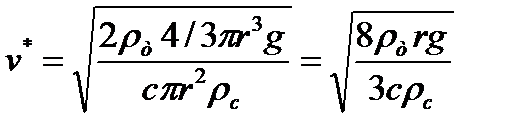
Примем r = 0,1 м, ρ = 0,8∙103 кг/м3 (дерево). Тогда для движения в воздухе (ρвозд= 1,29 кг/м3) получаем v * ≈ 18 м/с, в воде (ρводы ≈ 1∙103 кг/м3) v * ≈ 0,65 м/с, в глицерине (ρглицерина = 1,26∙103 кг/м3) v* ≈ 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение.
Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения - уравнение второго закона Ньютона с учетом двух сил, действующих на тело; силы тяжести и силы сопротивления среды:
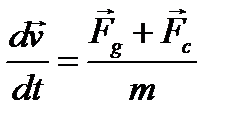 (1)
(1)
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
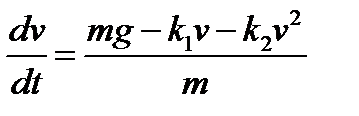 (2)
(2)
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (2), заданы? При такой постановке модель носит сугубо описательный характер. Понятно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, dv / dt=0, и соответствующую установившуюся скорость 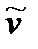 можно найти из условия mg – k 1 v – k 2 v 2=0, решая не дифференциальное, а квадратное уравнение. Имеем
можно найти из условия mg – k 1 v – k 2 v 2=0, решая не дифференциальное, а квадратное уравнение. Имеем
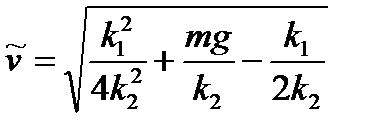 (3)
(3)
Итак, характер движения качественно таков: скорость при падении возрастает от v 0 до 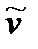 ; как и по какому закону - это можно узнать, лишь решив дифференциальное уравнение (2).
; как и по какому закону - это можно узнать, лишь решив дифференциальное уравнение (2).
Однако даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов. И хотя это не доказывает невозможность его аналитического решения путем подстановок, но они не очевидны. Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций - а как найти закон изменения во времени перемещения? - Формальный ответ прост: нужно проинтегрировать
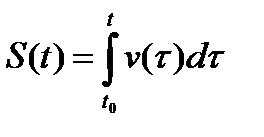 (4)
(4)
но шансы вычисление интеграла точно совсем невелики. Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс - а именно это есть цель моделирования.
Рассмотрим несколько примеров.
Задача 1. Свинцовый шар радиуса r=0.01 м падает с высоты h0=100 м на землю. Начальная скорость тела v0=0 м/c. Нужно выяснить, с какой скоростью он будет двигаться в момент соприкосновения с землей и сколько времени займет падение.
Решение. Будем использовать формулу (2). Для вычисления параметров воспользуемся табличными данными.
Рассчитаем массу тела: m= ρV, где плотность ρ= 11340 кг/м3; объем шара V=4/3πr3=4.19∙10-6 м3; таким образом, получаем m=0,04750 кг.
Коэффициент линейного сопротивления среды для шара k 1= 6πμr (формула Стокса), где μ = 0,0182 Н∙с∙м-2 – динамическая вязкость воздуха при нормальных условиях (t = 20°С и давлении 1 атм.), r - радиус шарика. Так, для указанных выше параметров, получим k1= 0,00343 Н∙с/м.
Коэффициент квадратичного сопротивления среды равен k 2 = 0,5сSρсрeды, где с=0,4 - коэффициент лобового сопротивления выберем для шара согласно рис. 1. Подставляя в расчетную формулу площадь поперечного сечения шара S=0,0003142 м2 и плотность воздуха при нормальных условиях ρвозд.=1,29кг/м3, получим значение коэффициента k2=0,0000811 кг c/м.
Будем решать уравнение при найденных параметрах, приближая значения производной конечными разностями.
Заменим значения производной скорости 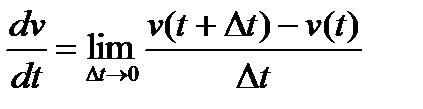 приближенными значениями конечных разностей
приближенными значениями конечных разностей
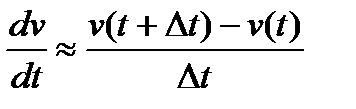 (5)
(5)
При подстановке в (2) это дает
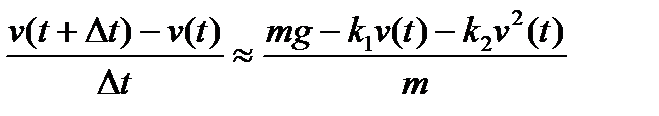 (6)
(6)
Выражая скорость, получим
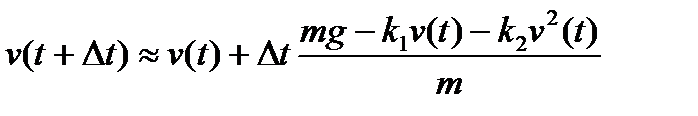 (7)
(7)
Так как при падении тела высота уменьшается, то с учетом малого изменения скорости за время Δt движение можно считать приближенно равномерным, и расчет высоты в момент времени t+Δt осуществлять по формуле
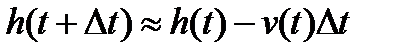 (8)
(8)
Окончательно, задав t0=0c, малое значение Δt=0,05 с, tn=tn-1+ Δt, v(t0)=0м/с, h0=100 м, для n=1, 2, 3,… можно последовательно вычислить значения
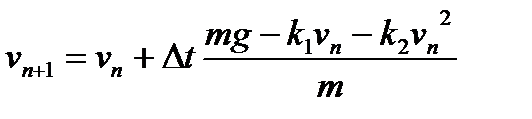 (9)
(9)
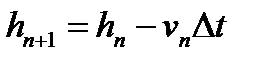 (10)
(10)
Условием окончания расчетов является падение тела на землю, т.е. последним является шаг, на котором высота станет равна нулю.
Задача 2. Свинцовый шар радиуса r=0.01 м тонет в воде. Начальная скорость тела v0=0 м/c. Нужно выяснить, в какой момент времени движение станет равномерным и какая скорость падения при этом будет достигнута.
Решение задачи 2 осуществляется также по формулам (9) и (10), так как падение в воде подчиняется тем же законам движения, что и падение тела в воздухе. Нужно только пересчитать значение коэффициентов сопротивления, т.к. они зависят от среды.
Используя табличные данные динамической вязкости воды при нормальных условиях μ=1,002 Нс/м2, ее плотность ρводы=1000кг/м3, получаем значения коэффициентов k1= 0,1889Нс/м, k2=0,0628кг c/м.
Условием окончания расчетов будет стабилизация скорости падения тела, т.е. 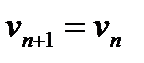 .
.
Задачи 1 и 2 могут быть легко модифицированы для изучения движения тела каплевидной формы в тех же условиях. Для этого необходимо подставить значение коэффициента лобового сопротивления с=0,45 для капли (см. рис. 1), учесть уменьшение поперечного сечения тела при «вытягивании хвостика» капли и пересчитать значение коэффициентов k1, k2.
Задача 3. Свинцовый шар радиуса r=0.01 м вылетает из рогатки, находящейся на высоте h0 м со скоростью v0 м/c под углом α к горизонту. Нужно выяснить дальность полета и максимальную высоту подъема тела, а так же с какой скоростью он будет двигаться в момент соприкосновения с землей и сколько времени займет падение.
Решение. Так как движение нельзя считать линейным, рассмотрим проекции уравнения (1) на координатные оси (ось OX направлена вправо, OY - вверх).
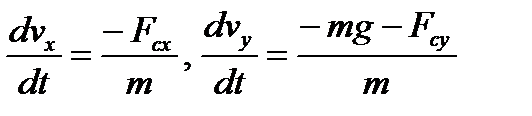 (11)
(11)
Подставим значение силы сопротивления, в силу принципа суперпозиции получим
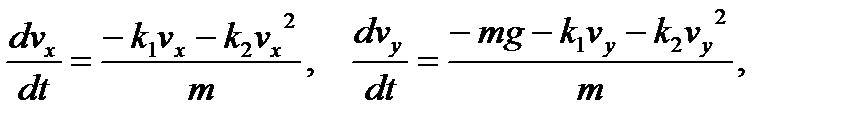 (12)
(12)
Значения коэффициентов сопротивления возьмем из задачи 1. Проекции начальной скорости на координатные оси 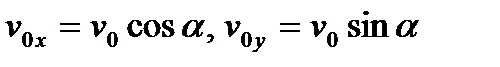 . С учетом формул (5) и (8), горизонтальная составляющая скорости и дальность полета будет описываться соотношениями
. С учетом формул (5) и (8), горизонтальная составляющая скорости и дальность полета будет описываться соотношениями
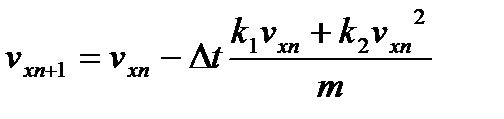 (13)
(13)
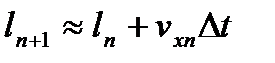 (14)
(14)
Для описания движения по вертикали следует учесть, что тело будет вначале подниматься
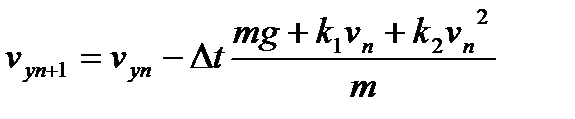 (15)
(15)
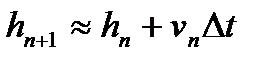 (16)
(16)
А затем, после полного торможения тела (vyn+1=0), оно начнет падать вниз:
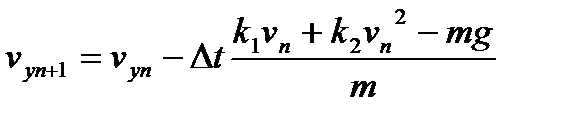 (17)
(17)
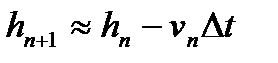 (18)
(18)
Условие окончания всех вычислений – падение тела, т.е. hn+1=0.
Задавая разные значения угла α, можно сравнить максимальные дальность и высоту подъема тела.
3. Построение компьютерной модели движения тела с учетом сопротивления среды в программе MS Excel
Для построения компьютерных моделей можно использовать различные компьютерные программы. Существуют специализированные программные средства, предназначенные для построения физических моделей. Однако нам достаточно возможностей табличного процессора MS Excel, который позволяет как производить вычисления, так и наглядно представлять результаты вычислений.
Будем использовать следующие способы представления результатов:
1) таблицы значений найденных величин
2) графики, полученные по табличным данным, по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса.
3.1. Построение модели свободного падения свинцового шарика с учетом сопротивления воздуха
Решим в MS Excel задачу 1 п. 2.3. Для этого зададим начальные и справочные значения, используемые при решении задачи 1:
Таблица 1.
Характеристики свинцового шара
| A | B | C | D | E | F | G | H | I | |
| 1 | g= | 9,8 | m/c^2 | ρ= | 11340 | кг/м^3 | m= | 0,04750 | кг |
| 2 | h0= | 100 | м | r= | 0,01 | м | S= | 0,0003142 | m^2 |
| 3 | v0= | 0 | м/с | c= | 0,4 |
Для расчета требуются плотность и динамическая вязкость воздуха (справочные данные) и значения коэффициентов сопротивления, вычисленные в задаче 1:
Таблица 2.
Плотность и динамическая вязкость воздуха, коэффициенты сопротивления
| A | B | C | |
| 6 | воздух | ||
| 7 | μ= | 0,0182 | Нс/м^2 |
| 8 | ρ_= | 1,29 | кг/м^3 |
| 9 | k1= | 0,00343 | Нс/м |
| 10 | k2= | 0,0000811 | кг c/м |
Проведем расчеты скорости и высоты тела по формулам (9) и (10). Для этого в столбце А зададим последовательные значения времени начиная с 0с с интервалом 0,05с. В ячейках B13 и C13 зададим начальные значения высоты и скорости. В ячейку B14 введем формулу расчета высоты (10), с учетом того, что значения времени находятся в столбце А, предшествующее значение высоты – в ячейке В13 и текущее значение скорости – в ячейке С14:
=B13-C14*(A14-A13)
Для вычисления скорости в ячейку С14 введем формулу, соответствующую (9):
=C13+(H$2*B$2-B$9*C13-B$10*C13*C13)/H$2*(A14-A13)
Поскольку в формулу входят постоянные параметры, ссылки на соответствующие ячейки (см. таблицы 1, 2) записываем в смешанной форме, чтобы они не изменялись при копировании. Наконец, для контроля окончания вычислений, в ячейку D14 вводим проверку условия падения тела (высота при движении должна оставаться положительной):
=ЕСЛИ(B14<=0;"падение";"")
Для проведения расчетов дальше нужно выделить диапазон ячеек B14:D14 и протянуть выделение вниз для копирования формул. Завершить протягивание нужно при появлении в столбце D надписи «падение». Приведем в таблице 3 часть расчетных формул, а в таблице 4 – вычисленные значения. Полностью результаты расчетов для этой задачи приведены в приложении 1.
Таблица 3.
Формулы для расчета высоты и скорости падения в воздухе
| A | B | C | D | |
| 12 | t | h | v | |
| 13 | 0 | =B3 | =B4 | |
| 14 | 0,05 | =B13-C14*(A14-A13) | =C13+(H$2*B$2-B$9*C13-B$10*C13*C13)/H$2*(A14-A13) | =ЕСЛИ(B14<=0;"падение";"") |
| 15 | 0,1 | =B14-C15*(A15-A14) | =C14+(H$2*B$2-B$9*C14-B$10*C14*C14)/H$2*(A15-A14) | =ЕСЛИ(B15<=0;"падение";"") |
Таблица 4.
Часть расчета высоты и скорости падения в воздухе
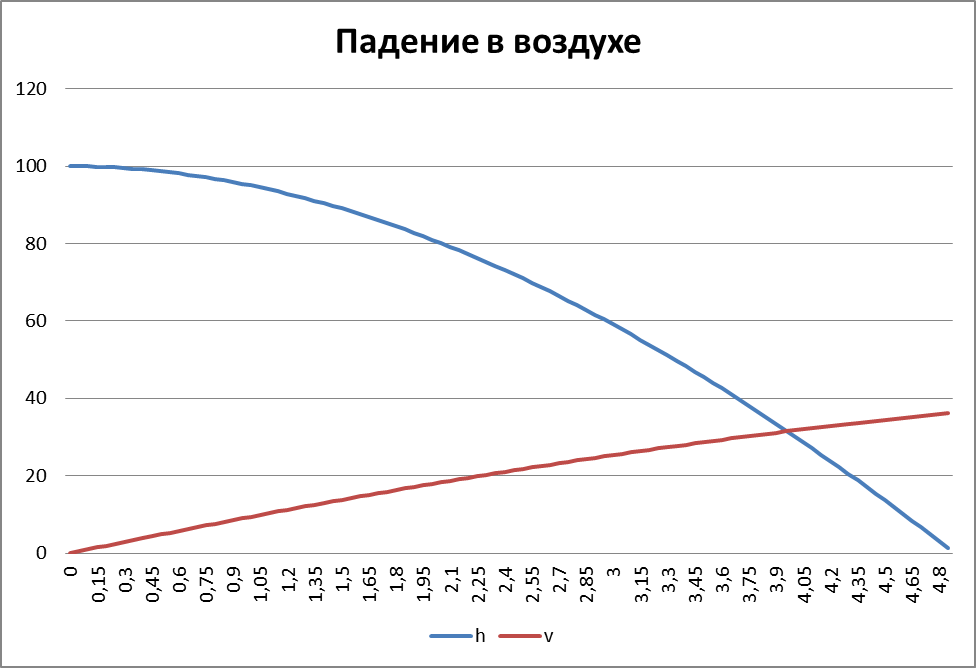
| A | B | C | D | |
| 12 | t | h | v | |
| 13 | 0 | 100 | 0 | |
| 14 | 0,05 | 99,9755 | 0,49 | |
| 15 | 0,1 | 99,927 | 0,978 | |
| 16 | 0,15 | 99,853 | 1,465 | |
| 17 | 0,2 | 99,756 | 1,949 | |
| … | ||||
| 108 | 4,75 | 4,847 | 35,794 | |
| 109 | 4,8 | 3,045 | 36,045 | |
| 110 | 4,85 | 1,230 | 36,294 | |
| 111 | 4,9 | -0,597 | 36,541 | падение |
Результаты проведения расчетов можно представить графически. Для этого вставим на рабочий лист диаграмму (график) для рядов данных B12:B110 (высота тела) и C12:C110 (скорость падения), в качестве подписей по оси OX используем значения времени из диапазона A12:A110. Результаты представлены на рис. 1. Из рисунка видно, что высота меняется по квадратичной зависимости (график – парабола), что означает торможение тела из-за сопротивления воздуха. По графику скорости это менее заметно, т.к. скорость при падении растет, но медленно.