Задание № 29. Дифференциальные уравнения в частных производных
первого порядка
Найти общие решения уравнений.
Найти общее решение уравнения.
Найти поверхность, удовлетворяющую данному уравнению и проходящему через линию.
1. 
; 
; 
;
; 
.
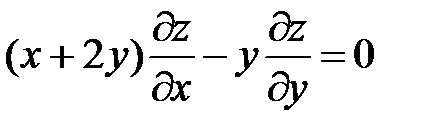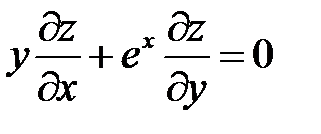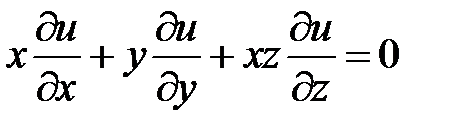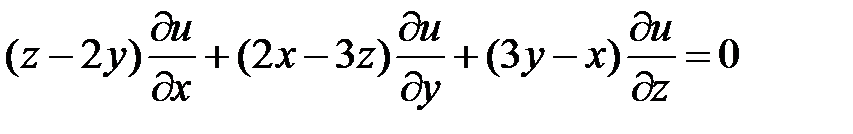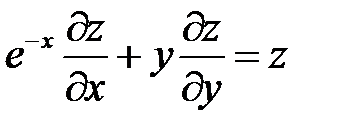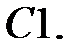
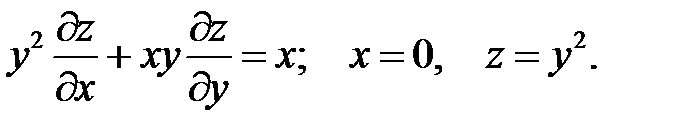
2. 
.
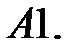
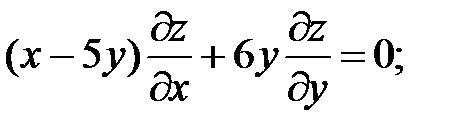
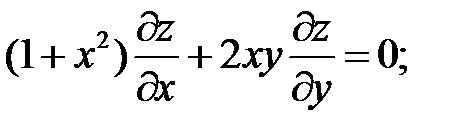
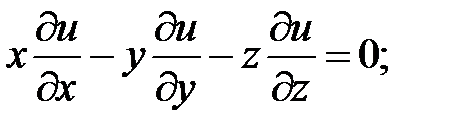
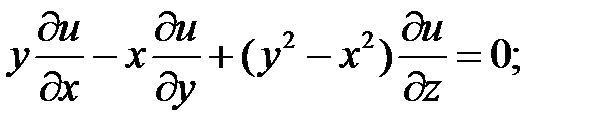
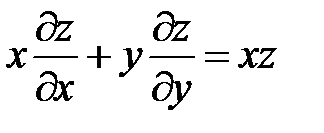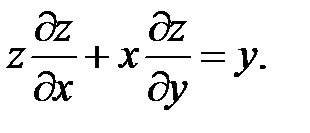
3. 
.
.
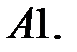
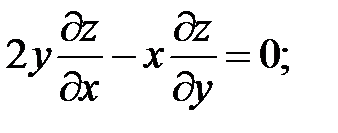
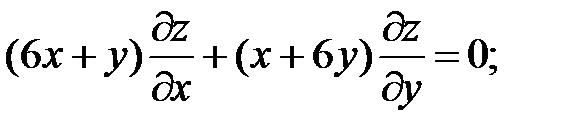
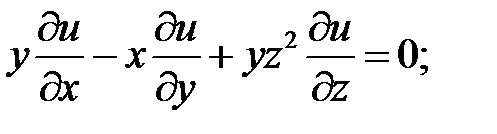
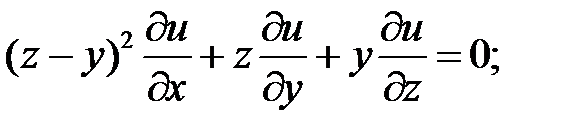
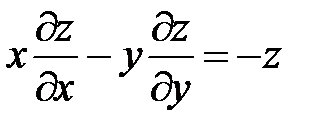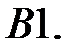
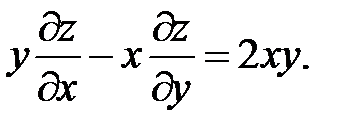
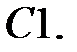
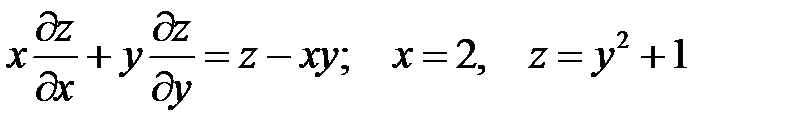4. 
.
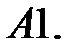
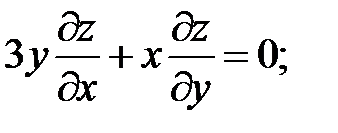
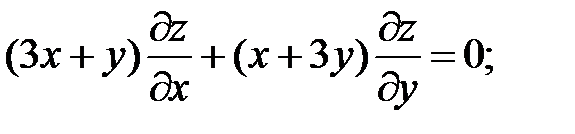
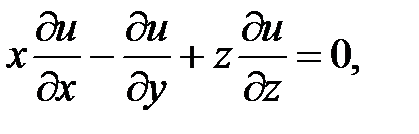
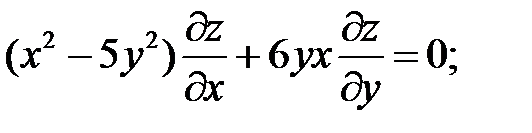
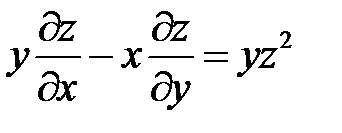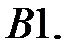
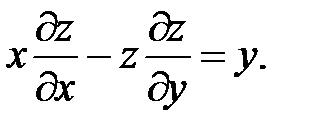
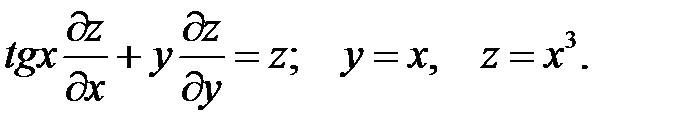
5. 
.
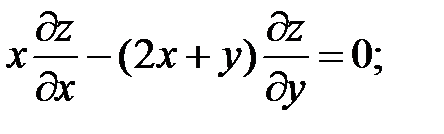
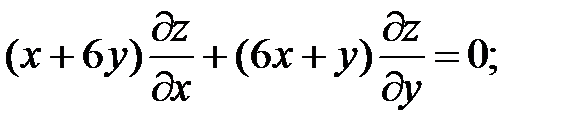
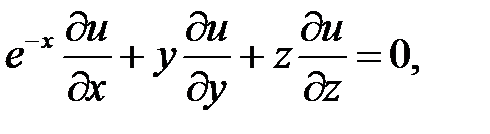
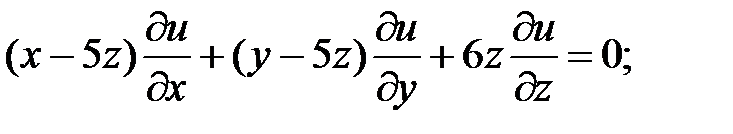
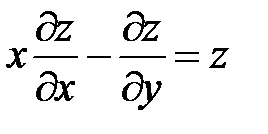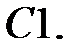
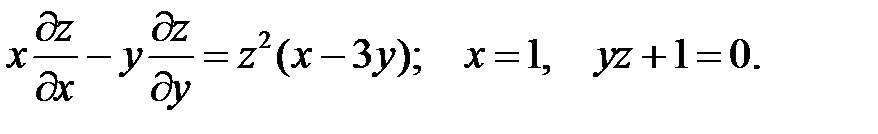
6. 
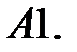
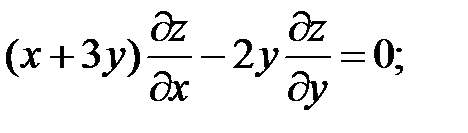
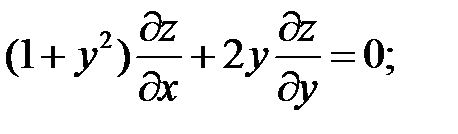
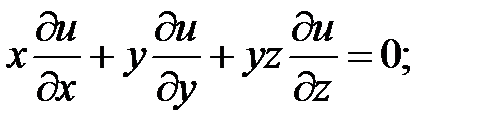
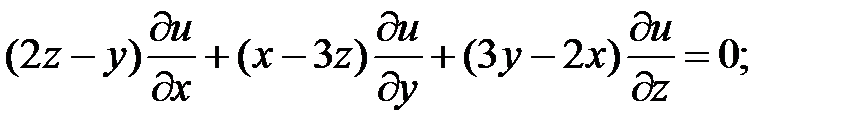
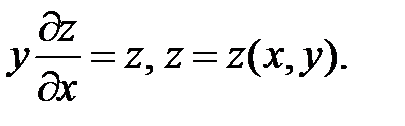
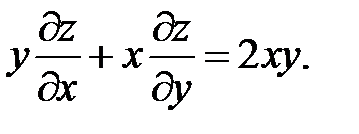
7. 
.
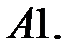
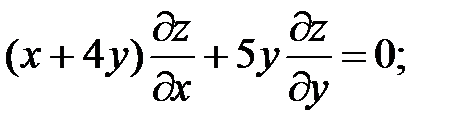
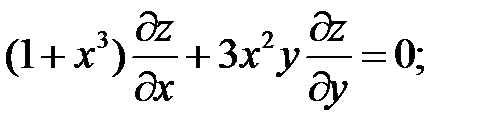
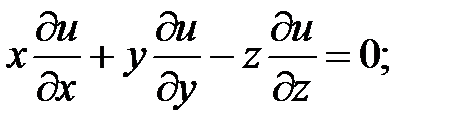
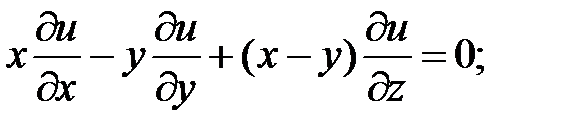
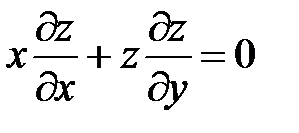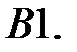
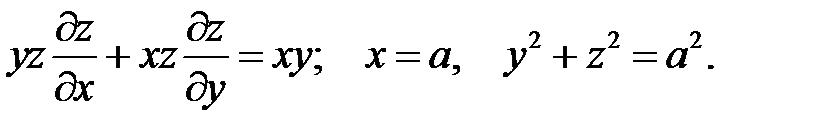
8. 
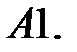
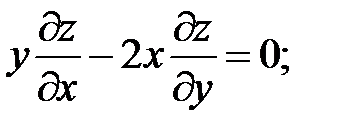
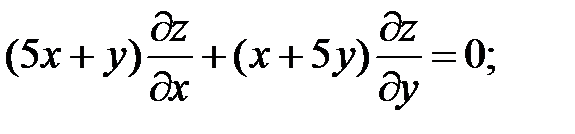
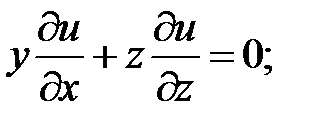
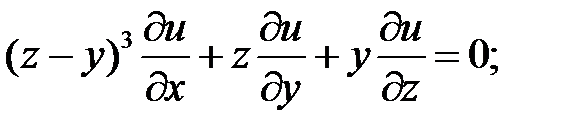
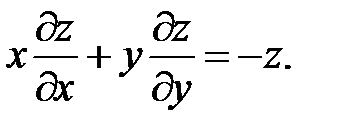
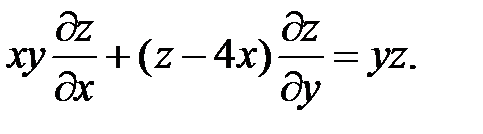
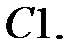
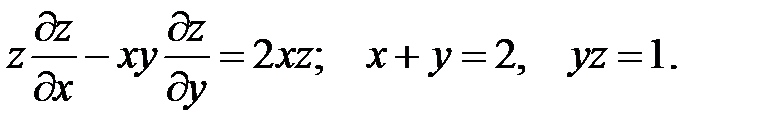
9. 
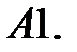
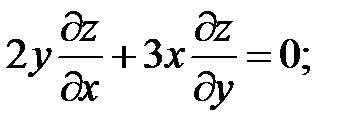
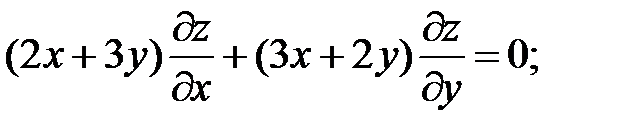
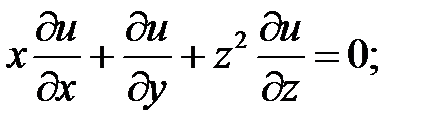
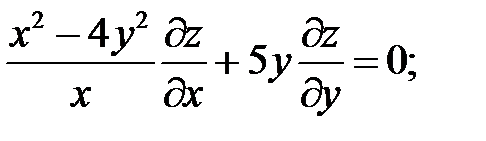
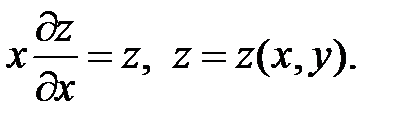
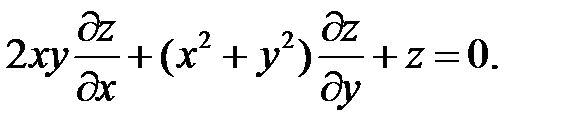
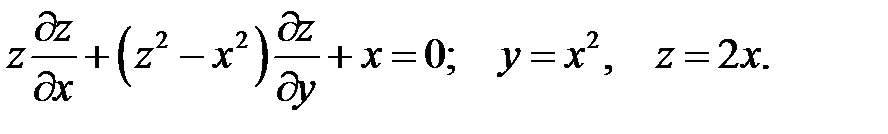
10. 
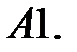
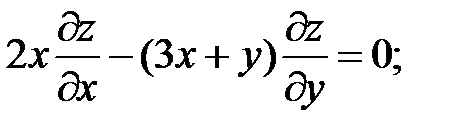
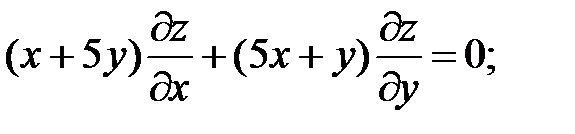
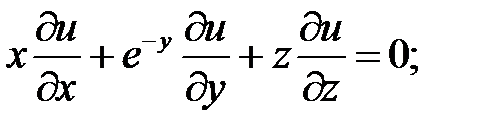
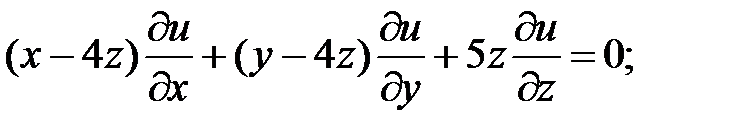
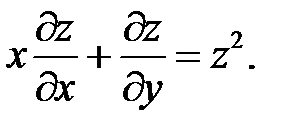
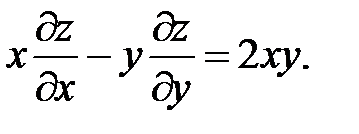
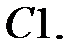
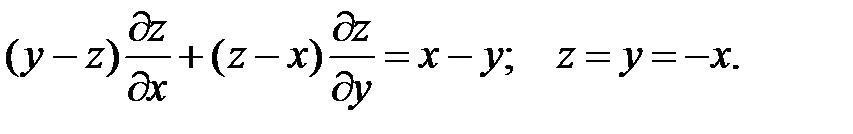
11. 
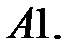
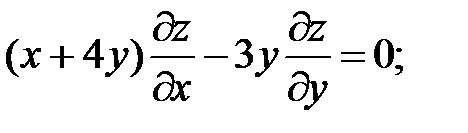
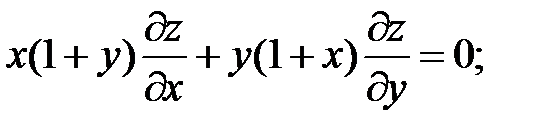
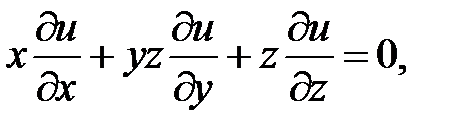
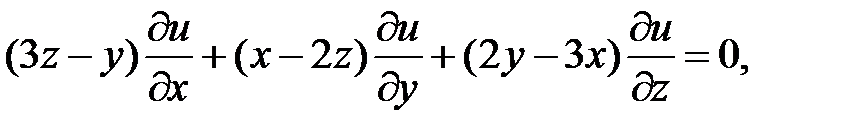
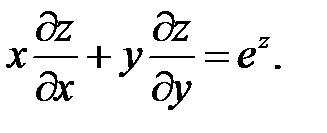
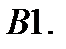
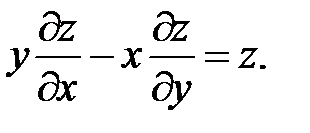
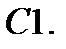
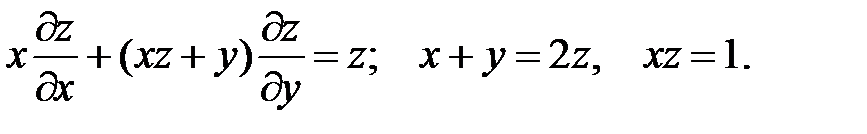
12. 
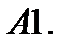
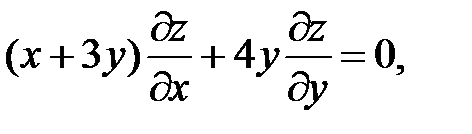
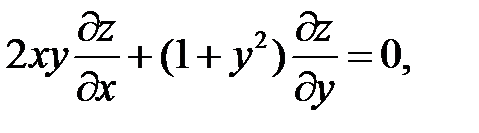
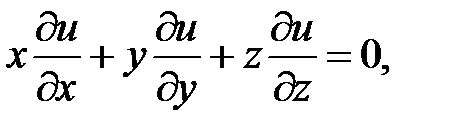
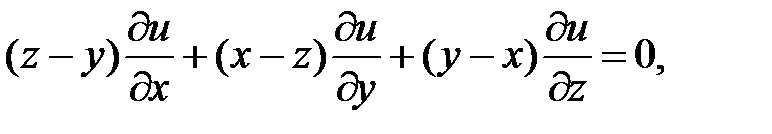
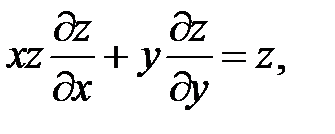
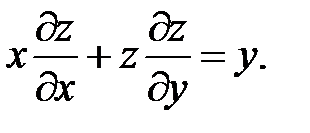
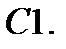
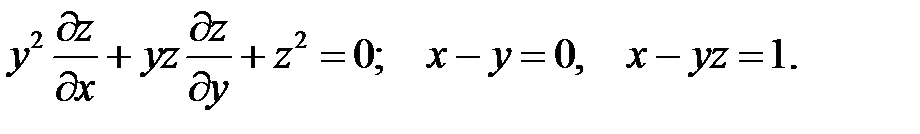
13. 
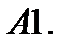
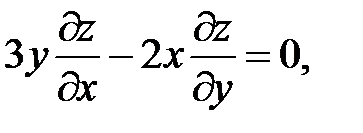
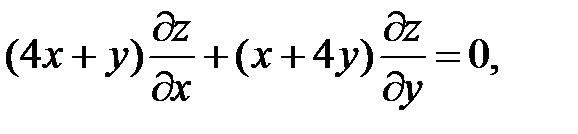
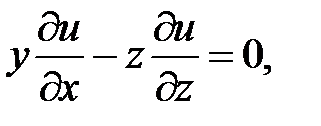
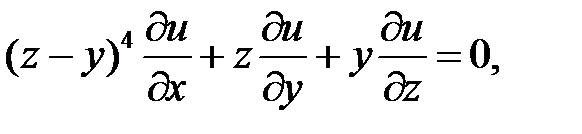
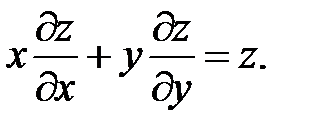
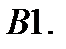
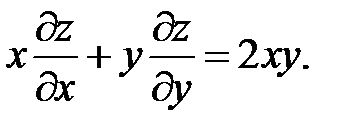
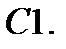
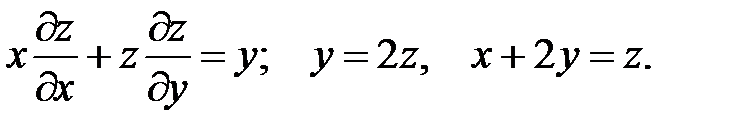
14. 
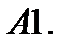
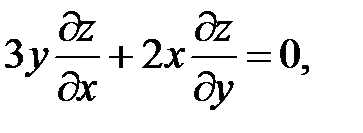
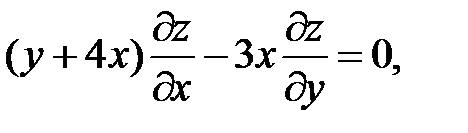
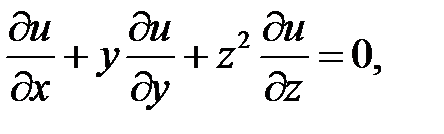
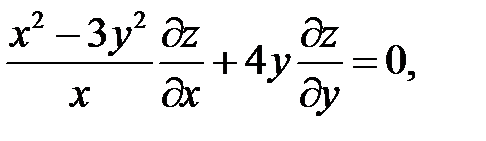
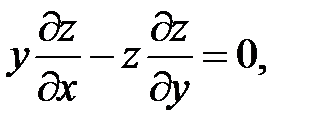
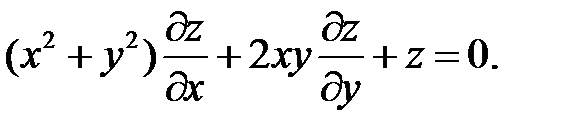
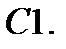
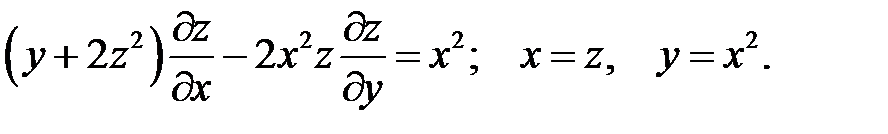
15. 
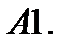
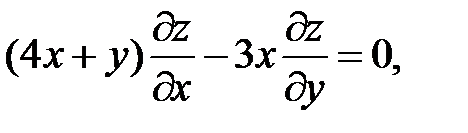
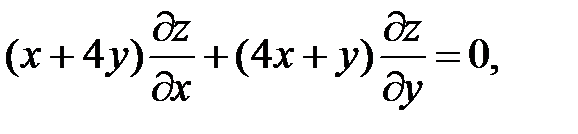
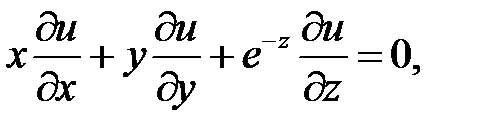
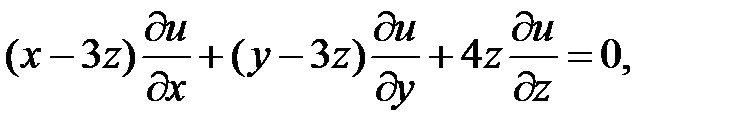
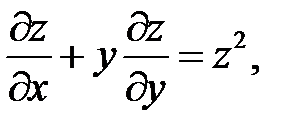
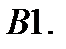
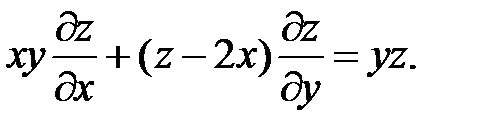
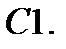
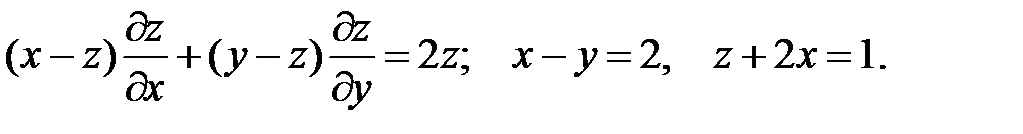
16. 
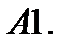
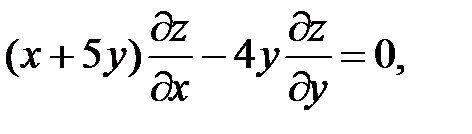
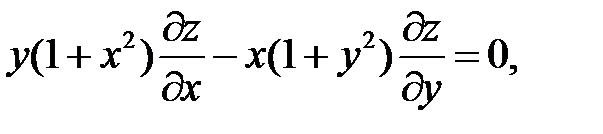
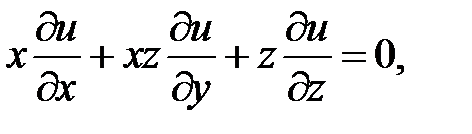
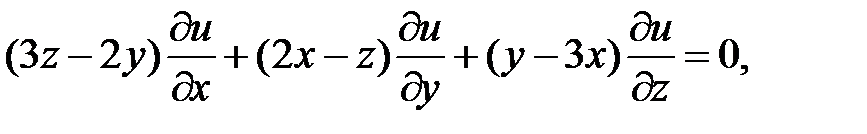
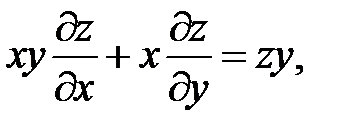
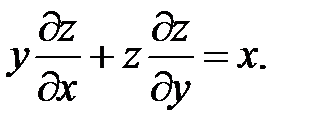
17. 
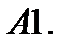
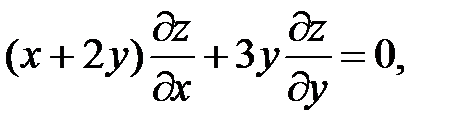
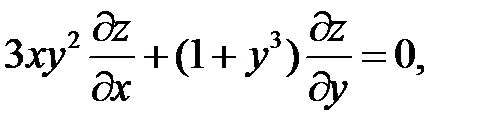
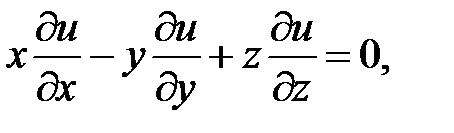
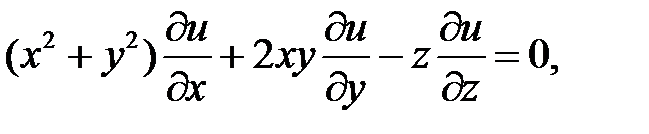
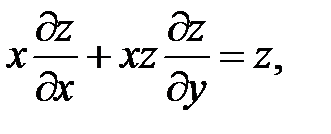
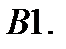
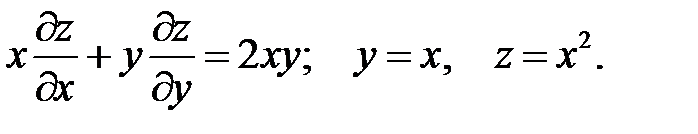
18. 
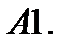
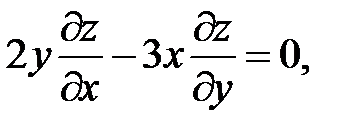
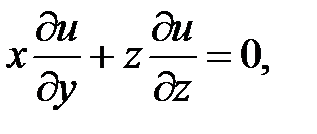
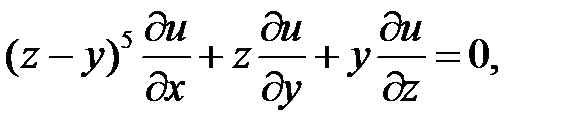
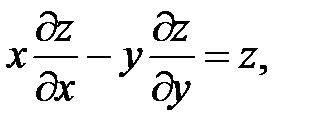
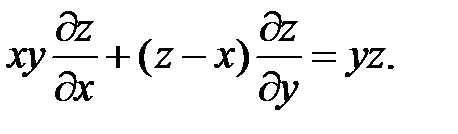
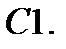
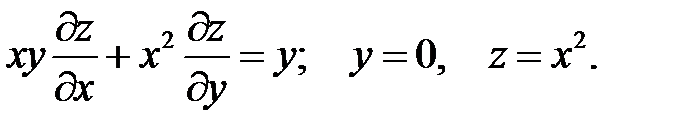
19. 
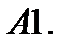
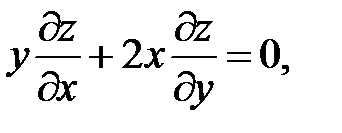
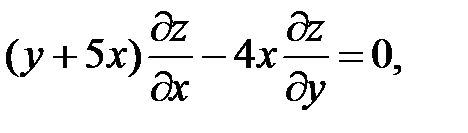
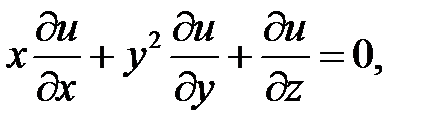
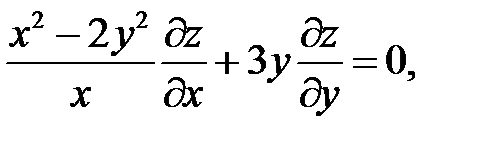
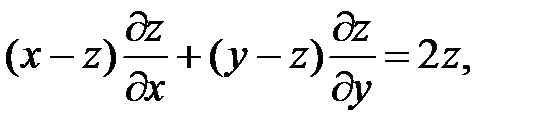
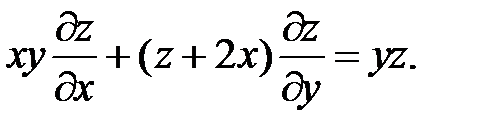
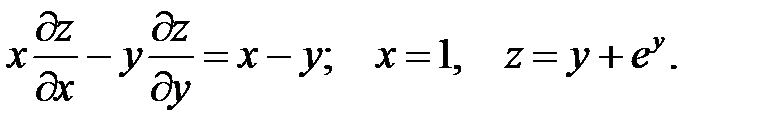
20. 
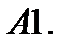
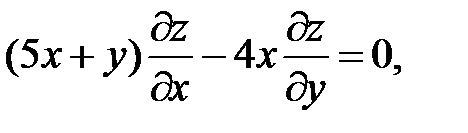
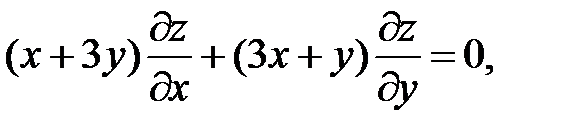
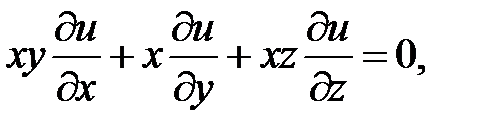
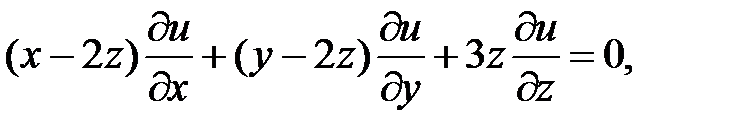
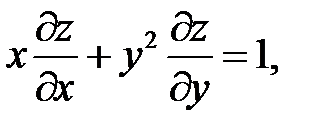
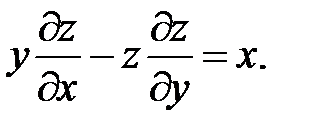
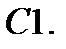
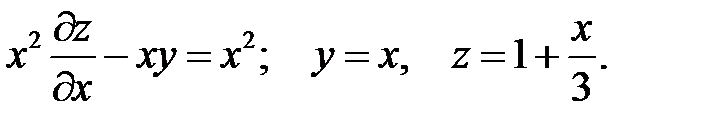
21. 
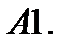
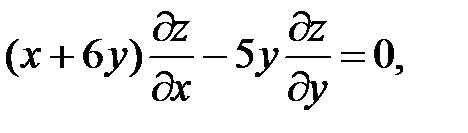
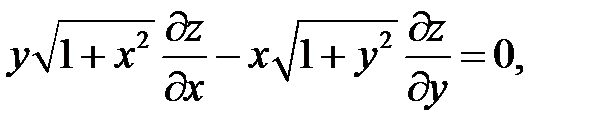
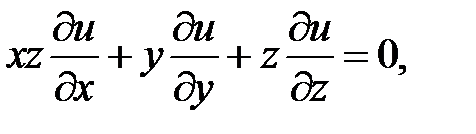
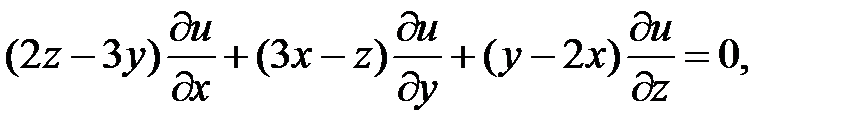
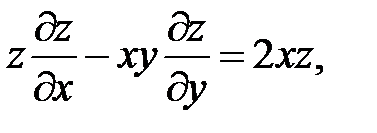
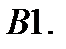
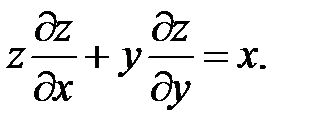
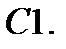
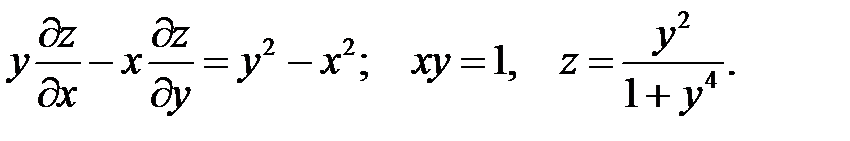
22. . 
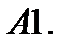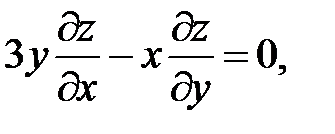
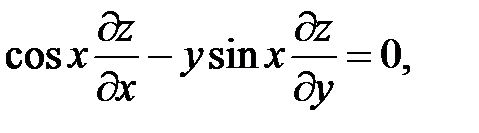
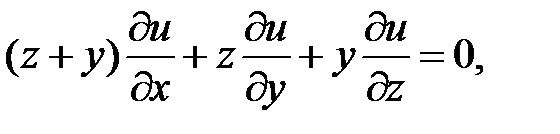
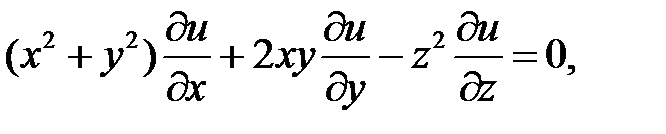
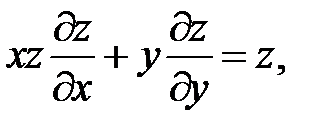
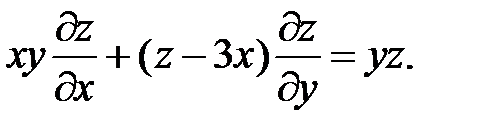
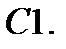
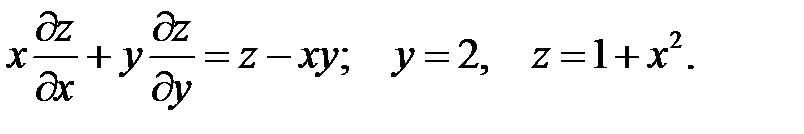
23. 
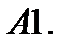
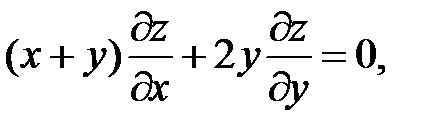
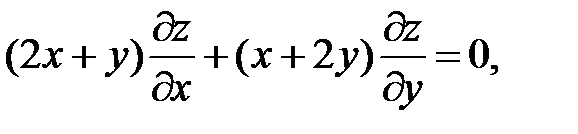
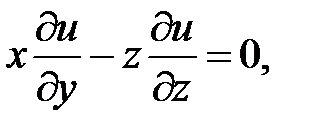
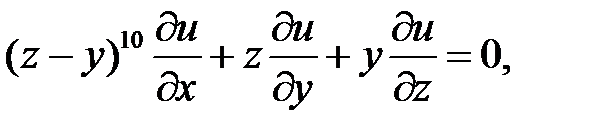
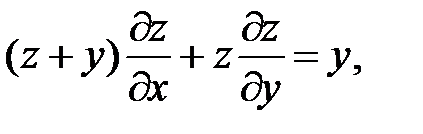
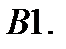
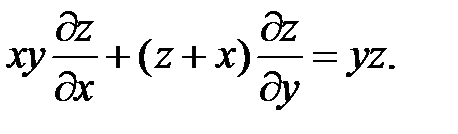
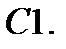
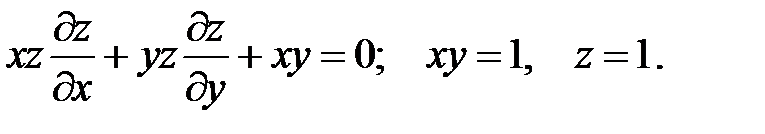
24. 
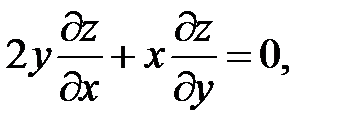
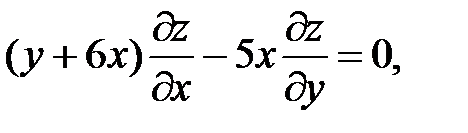
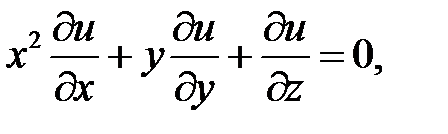
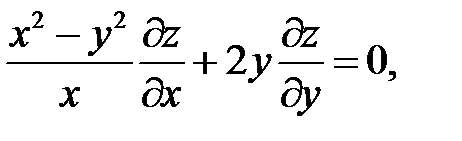
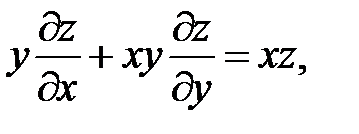
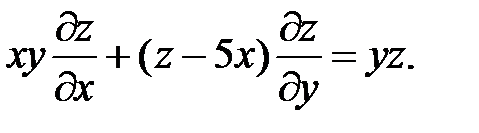
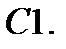
25. 
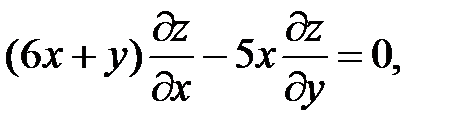
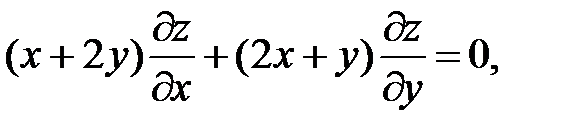
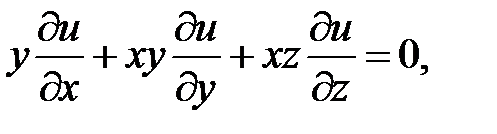
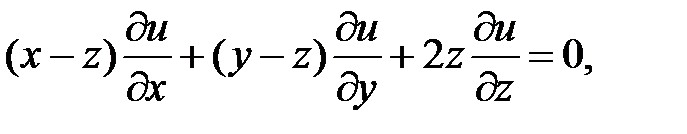
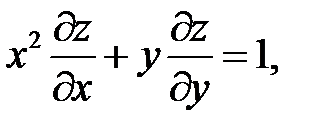
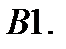
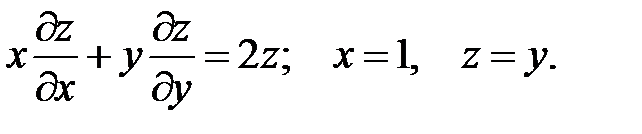
7.3. Вопросы и задачи для повторения
1. Что такое дифференциальное уравнение с частными производными? Что называется его решением? Какой геометрический смысл имеет решение уравнения с двумя независимыми переменными?
2. Какое уравнение называется линейным уравнением с частными производными первого порядка? В каком случае оно называется однородным? Неоднородным?
3. Как ставится задача Коши для уравнения с частными производными первого порядка? Какой геометрический смысл она имеет в случае двух независимых переменных?
4. Как построить общее решение однородного линейного уравнения с частными производными первого порядка? Как решается задача Коши для этого уравнения?
5. Как построить общее решение неоднородного линейного уравнения с частными производными первого порядка? Как решается задача Коши для этого уравнения?
6. При каком условии нормальная система двух уравнений с частными производными вполне интегрируема? Как интегрируется эта система при выполнении условия полной интегрируемости?
7. Какой вид имеет уравнение Пфаффа? При каком условии оно вполне интегрируемо? Как интегрируется это уравнение?
Решить уравнения.
8. 
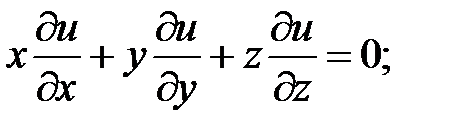
9. 
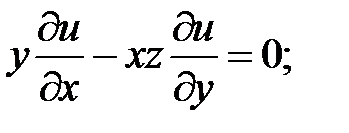
10. 
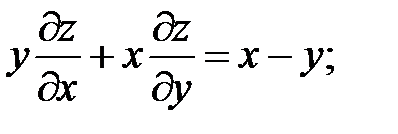
11. 
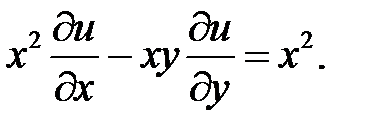
12. Имеет ли задача Коши
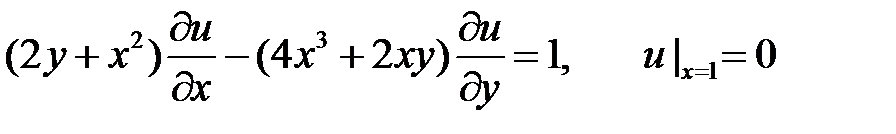
решение в окрестности точки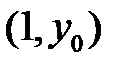 
и единственно ли оно?
Найти интегральные поверхности, проходящие через заданные кривые.
13. 
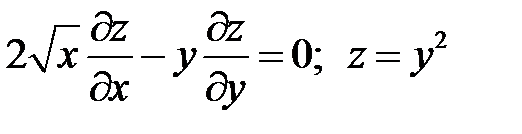при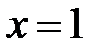 
.
14. 
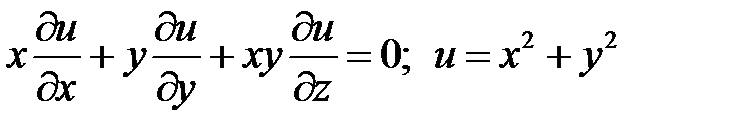при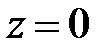 
.
15. Найти поверхность, проходящую через прямую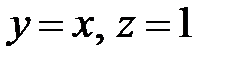 
и ортогональную к поверхностям 
.
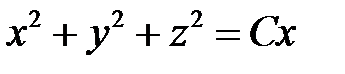16. Проинтегрировать уравнение Пфаффа
,
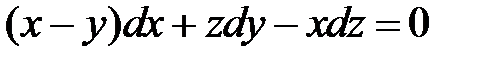доказав предварительно, что оно вполне интегрируемо.
17. Проинтегрировать следующую систему, доказав предварительно, что она интегрируема:
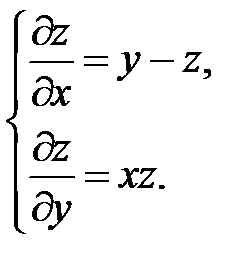
18. Построить базис первых интегралов систем:
а)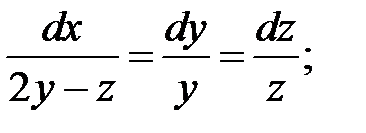 
б)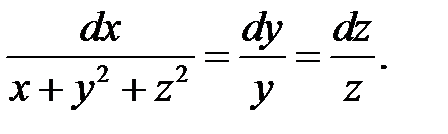 
19. Среди поверхностей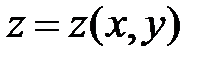 
пространства 
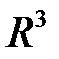выделить те, все нормали которых пересекают ось 
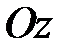. Найти ту из поверхностей, которая проходит через параболу 
.
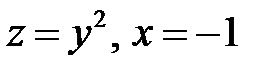Указание. Воспользоваться условием, что в любой точке поверхности вектор нормали к поверхности, радиус-вектор этой точки и орт оси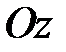 
компланарны.
20. Среди поверхностей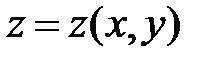 
пространства 
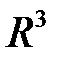выделить те, все нормали которых пересекают прямую 
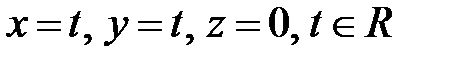. Найти ту из полученных поверхностей, которая в плоскости 
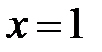проходит через параболу 
.
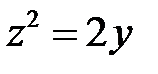Указание. Воспользоваться условием, что в произвольной точке поверхности вектор нормали к поверхности, радиус-вектор этой точки и направляющий вектор данной прямой компланарны.
21. В пространстве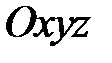 
найти поверхности, касательные плоскости к которым отсекают на оси 
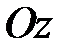отрезок постоянной длины 
.
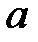СПИСОК ЛИТЕРАТУРЫ
1. Бибиков Ю.Н. Курс обыкновенных дифференциальных уравнений. – Издательство «Лань», 2011. – 304 с.
2. Боярчук А.К., Головач Г.П. Справочное пособие по высшей математике. Т. 5. Дифференциальные уравнения в примерах и задачах. – М.: Эдиториал УРСС, 2001. – 384 с.
3. Есипов А.А., Сазонов Л.И., Юдович В.И. Практикум по обыкновенным дифференциальным уравнениям. – М.: Вузовская книга, 2001. – 395 с.
4. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. – М.: Наука, 1971. – 576 с.
5. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. – Минск: Вышэйшая школа, 1974. – 766 с.
6. Обыкновенные дифференциальные уравнения в примерах и задачах / М.П. Григорьев, Ю.Т. Половинкин, Н.А. Романова, Е.Т. Софронов, Ю.И. Трофимцев. – М.: Вузовская книга, 2019. – 245 с.
7. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - М.: ФИЗМАТЛИТ, 2009. – 208 c.
8. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1974. – 331 c.
9. Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения: примеры и задачи. – М.: Высшая школа, 1989. – 383 c.
10. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. - М.: ФИЗМАТЛИТ, 2002. – 256 с.
11. Филиппов А.Ф. Введение в теорию дифференциальных уравнений. – ЛЕНАНД, 2022. – 240 с.
Учебное издание
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ:
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
В двух частях
Часть 2
Печатается в авторской редакции
Подписано в печать: Формат 60х84 /16.
Гарнитура «Таймс». Печать цифровая
Печ. л. 13,2 Тираж 50 экз. Заказ №
Издательский дом Северо-Восточного федерального университета
677891, г. Якутск, ул. Петровского, 5
Отпечатано в типографии ИД СВФУ