Дифференциальные уравнения
В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
7.1. Построение общего решения
Пусть неизвестная функция 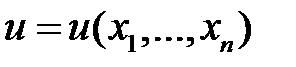 зависит от двух или более переменных. Уравнение вида
зависит от двух или более переменных. Уравнение вида
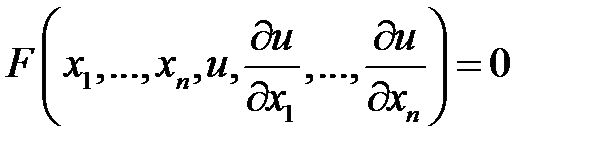 (1)
(1)
называется уравнением в частных производных первого порядка.
Функция 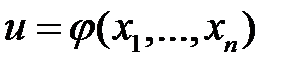 , обращающая
, обращающая 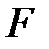 в нуль тождественно по
в нуль тождественно по 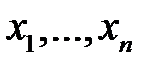 при подстановке вместо
при подстановке вместо 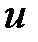 функции
функции 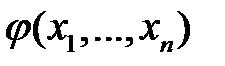 и вместо
и вместо 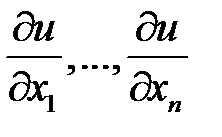 производных
производных 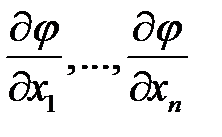 , называется решением уравнения (1). Решение уравнения (1) в
, называется решением уравнения (1). Решение уравнения (1) в 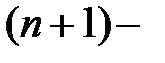 мерном пространстве
мерном пространстве 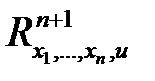 задает некоторую гладкую поверхность размерности
задает некоторую гладкую поверхность размерности 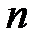 (гиперповерхность), которая называется интегральной поверхностью уравнения (1).
(гиперповерхность), которая называется интегральной поверхностью уравнения (1).
Линейным дифференциальным уравнением с частными производными первого порядка называется уравнение вида
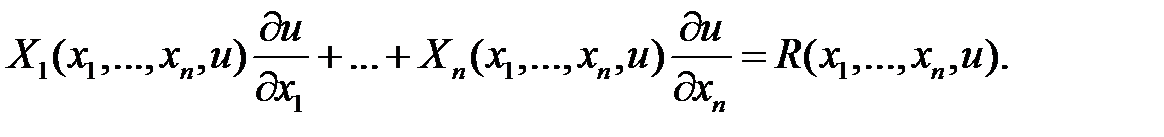 (2)
(2)
По способу нахождения общего решения различают два вида уравнений (2). Если в уравнении (2) 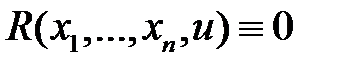 и все функции
и все функции 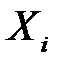 зависят только от независимых переменных
зависят только от независимых переменных 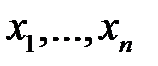 , то его называют линейным однородным уравнением с частными производными первого порядка. В противном случае, уравнение (2) называют линейным неоднородным уравнением с частными производными первого порядка или квазилинейным уравнением.
, то его называют линейным однородным уравнением с частными производными первого порядка. В противном случае, уравнение (2) называют линейным неоднородным уравнением с частными производными первого порядка или квазилинейным уравнением.
Рассмотрим уравнение первого типа:
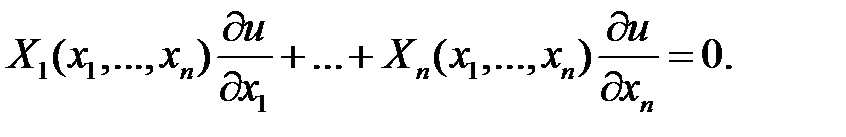 (3)
(3)
Предположим, что функции 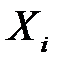 изменяются в некоторой области
изменяются в некоторой области 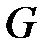 и в этой области непрерывно дифференцируемы. Кроме того, предположим, что в области
и в этой области непрерывно дифференцируемы. Кроме того, предположим, что в области 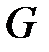
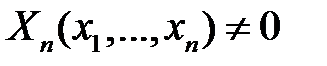 . Наряду с уравнением (3), рассмотрим систему обыкновенных дифференциальных уравнений в симметрической форме
. Наряду с уравнением (3), рассмотрим систему обыкновенных дифференциальных уравнений в симметрической форме
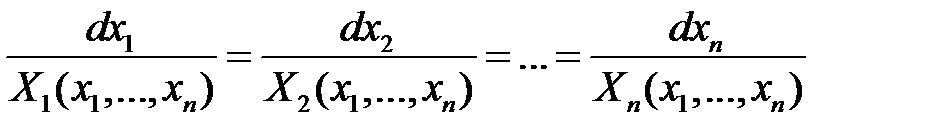 . (4)
. (4)
Эту систему уравнений можно записать в виде нормальной системы из 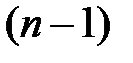 уравнений
уравнений
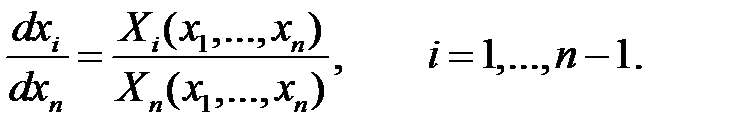 (5)
(5)
Пусть система уравнений (5) имеет 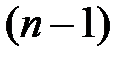 независимых первых интегралов. Справедлива следующая
независимых первых интегралов. Справедлива следующая
Теорема 1. Функция 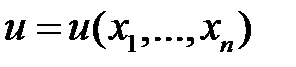 является решением линейного однородного уравнения (3) тогда и только тогда, когда она является первым интегралом системы уравнений (5).
является решением линейного однородного уравнения (3) тогда и только тогда, когда она является первым интегралом системы уравнений (5).
Пусть
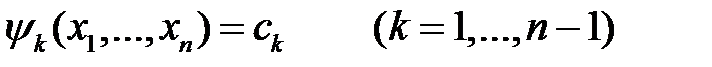
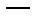 независимые первые интегралы системы уравнений (5). Тогда
независимые первые интегралы системы уравнений (5). Тогда
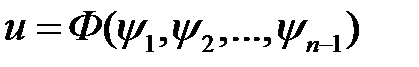 ,
,
где 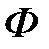
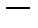 любая функция, непрерывно дифференцируемая по
любая функция, непрерывно дифференцируемая по 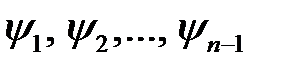 , будет общим решением уравнения (3).
, будет общим решением уравнения (3).
Пример 1. Найти общее решение уравнения 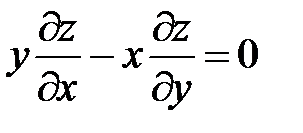 .
.
Решение. Уравнение характеристик:
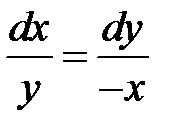
имеет первый интеграл 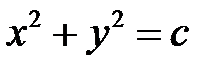 , а общее решение данного уравнения имеет вид
, а общее решение данного уравнения имеет вид
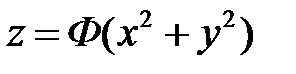 .
.
Пример 2. Найти общее решение уравнения
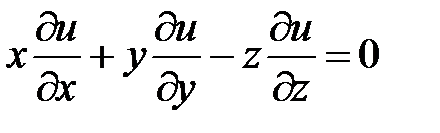 .
.
Решение. Составим систему уравнений в симметрической форме:
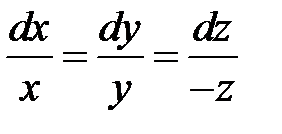 .
.
Эти уравнения имеют два независимых интеграла
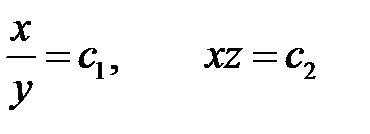 .
.
Тогда общее решение имеет вид
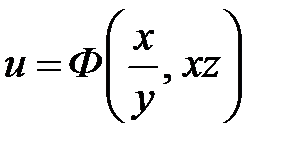 .
.
Пример 3. Найти общее решение уравнения
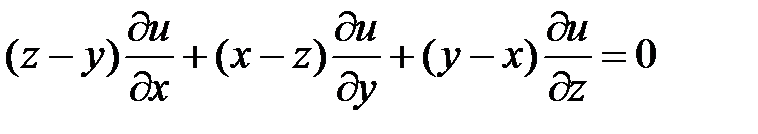 .
.
Решение. Составим систему уравнений
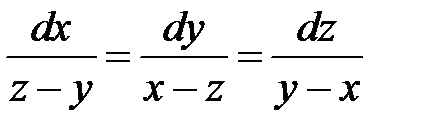 .
.
Пользуясь свойством пропорции, имеем
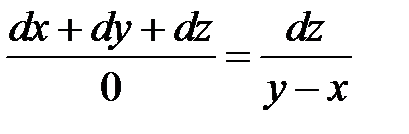 .
.
Отсюда 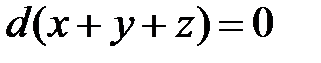 или
или 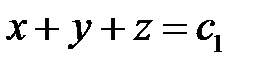 .
.
Находим второй интеграл. Для этого перепишем данное уравнение в виде
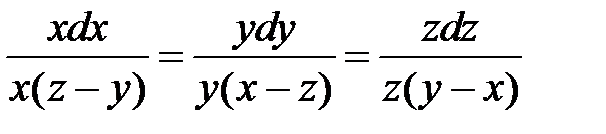 .
.
Отсюда
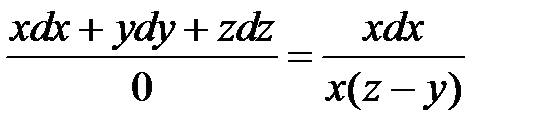 или
или 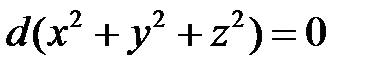 .
.
Интегрируя, получим второй интеграл 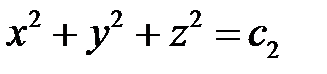 .
.
Общее решение имеет вид
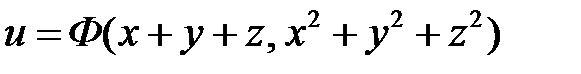 .
.
Теперь рассмотрим второй тип уравнения, т.е. уравнение вида (2). Уравнения характеристик запишутся так:
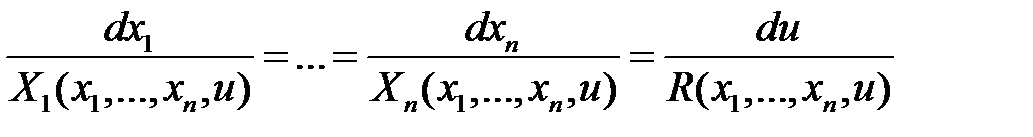 . (6)
. (6)
Пусть эта система уравнений имеет 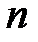 независимых первых интегралов
независимых первых интегралов
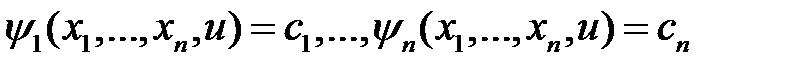 .
.
Тогда общее решение уравнения (2) записывают так:
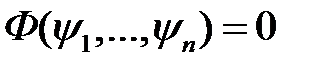 ,
,
где 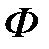
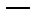 произвольная функция, непрерывно дифференцируемая по
произвольная функция, непрерывно дифференцируемая по 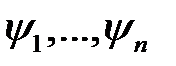 .
.
Пример 4. Найти общее решение уравнения
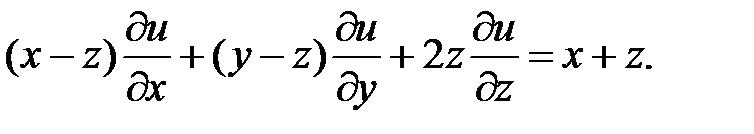
Решение. Составляем систему уравнений
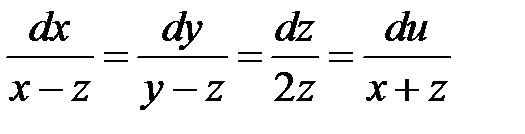 .
.
Из этой системы
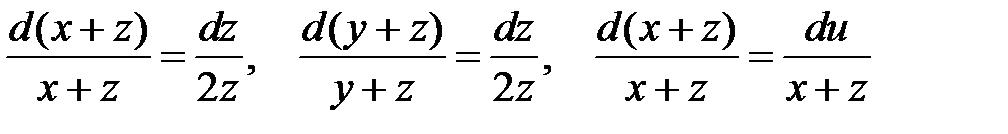 .
.
Тогда первыми интегралами системы будут выражения
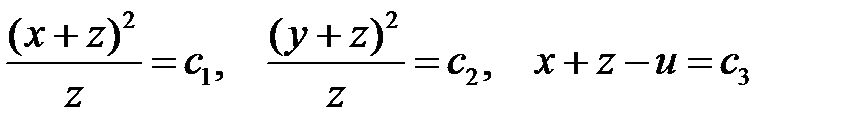 .
.
Общее решение имеет вид
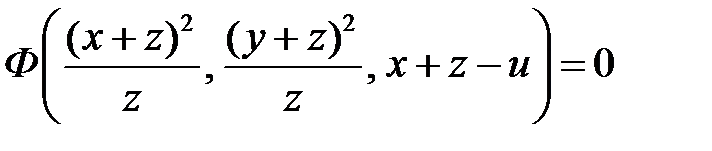 .
.
Чтобы найти поверхность 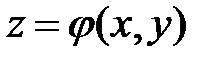 , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению
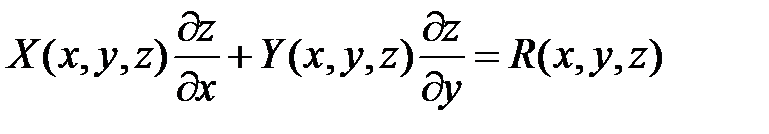 (7)
(7)
и проходящую через линию
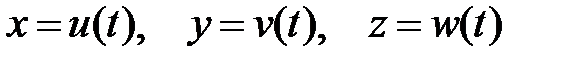 , (8)
, (8)
необходимо найти два независимых интеграла 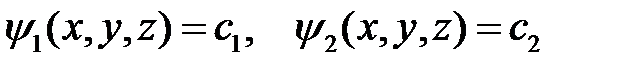 . В эти интегралы нужно подставить выражения (8)
. В эти интегралы нужно подставить выражения (8) 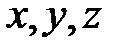 через параметр
через параметр 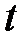 . Получим два выражения:
. Получим два выражения: 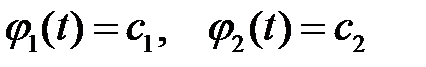 . Исключим из этих функций
. Исключим из этих функций 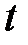 и получим соотношение
и получим соотношение 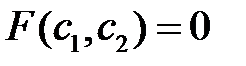 . Подставив сюда вместо
. Подставив сюда вместо 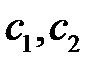 левые части интегралов, получим искомое решение.
левые части интегралов, получим искомое решение.
Пример 5. Найти интегральную поверхность уравнения
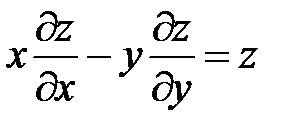 ,
,
если 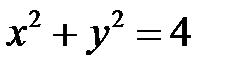 при
при 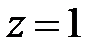 .
.
Решение. Система уравнений
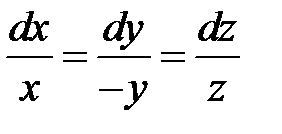
имеет интегралы
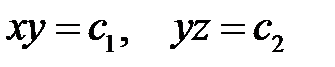 .
.
При 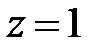 имеем
имеем 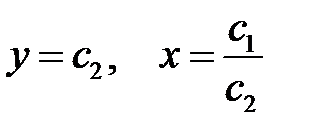 . Подставляя в уравнение
. Подставляя в уравнение 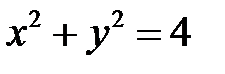 значения
значения 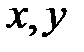 , получим
, получим
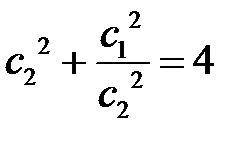 .
.
Тогда искомое решение имеет вид:
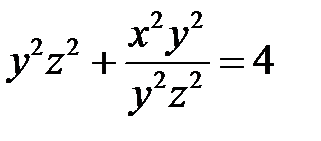 или
или 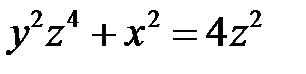 .
.
Пример 6. Найти интегральную поверхность уравнения
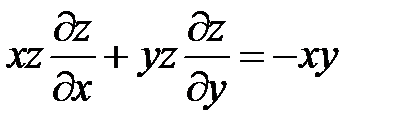 ,
,
проходящую через линию 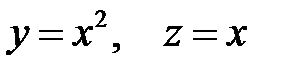 .
.
Решение. Система уравнений
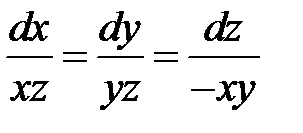
имеет первые интегралы
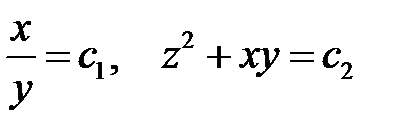 .
.
При 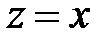 имеем
имеем
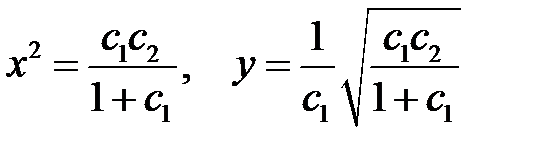 .
.
Отсюда получаем уравнение, связывающее 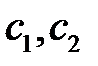 :
:
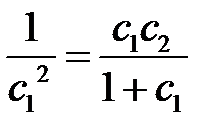 .
.
Подставив сюда значения 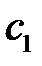 и
и 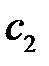 , имеем окончательно
, имеем окончательно
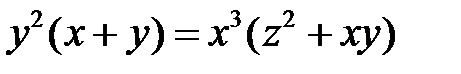 .
.
Пример 7.Найти поверхность, удовлетворяющую уравнению
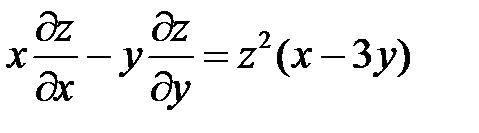
и проходящую через линию 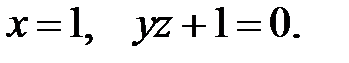
Решение. Находим первые интегралы системы:
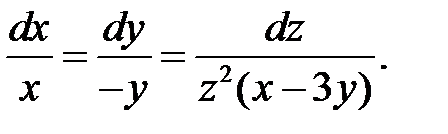
Из уравнения
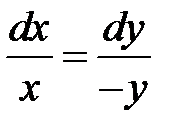
получаем 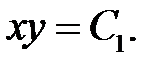 На основании свойства пропорции получаем следующую интегрируемую комбинацию:
На основании свойства пропорции получаем следующую интегрируемую комбинацию:
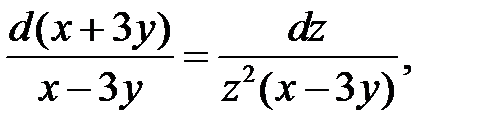
откуда интегрированием находим второй независимый интеграл 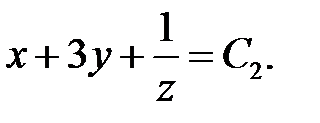
Следовательно, все решения исходного уравнения выражаются формулой
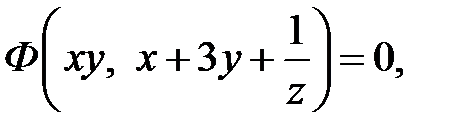
где 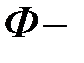 произвольная непрерывно дифференцируемая функция. Исключая переменные
произвольная непрерывно дифференцируемая функция. Исключая переменные 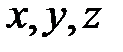 из соотношений
из соотношений
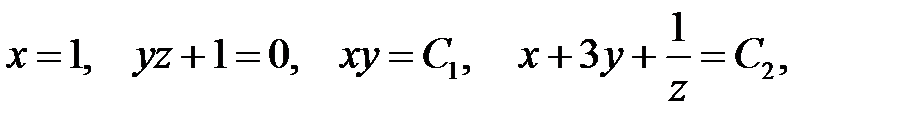
получим связь между 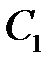 и
и 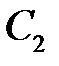 на кривой
на кривой 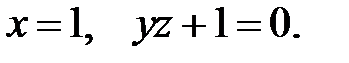 Имеем
Имеем
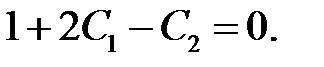
Подставляя в это соотношение значения 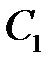 и
и 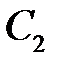 , получаем уравнение искомой поверхности:
, получаем уравнение искомой поверхности:
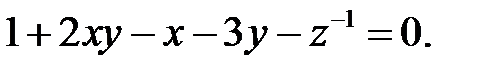
7.2. Индивидуальные задания








