Задание № 27. Особые точки на плоскости
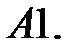 Начертить на фазовой плоскости траектории линейных систем
Начертить на фазовой плоскости траектории линейных систем 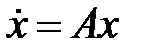 и исследовать их на устойчивость.
и исследовать их на устойчивость.
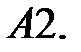 Найти и определить типы всех особых точек данных систем.
Найти и определить типы всех особых точек данных систем.
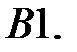 При каких значениях параметра
При каких значениях параметра 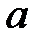 начало координат линейной системы
начало координат линейной системы 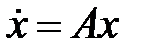 будет особой точкой указанного типа?
будет особой точкой указанного типа?
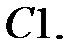 На фазовой плоскости начертить траектории нелинейной системы уравнений.
На фазовой плоскости начертить траектории нелинейной системы уравнений.
1. А1. 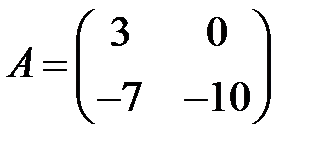 ;
; 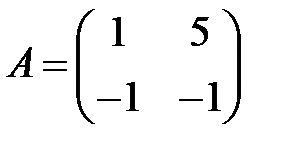 ;
; 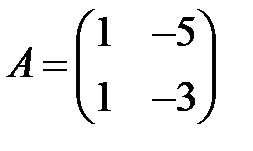 ;
; 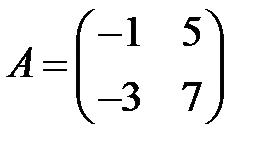 .
.
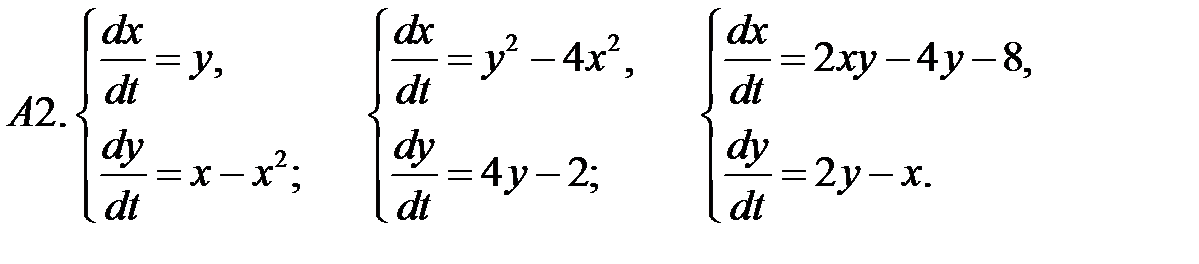
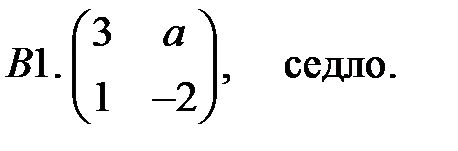
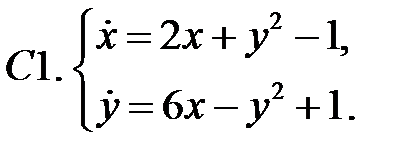
2. А1. 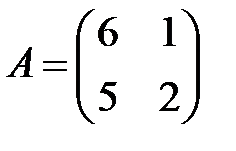 ;
; 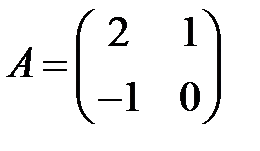 ;
; 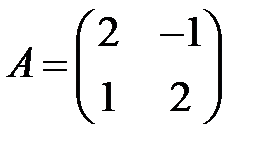 ;
; 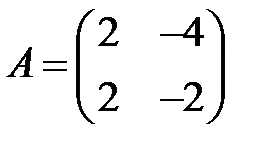 .
.
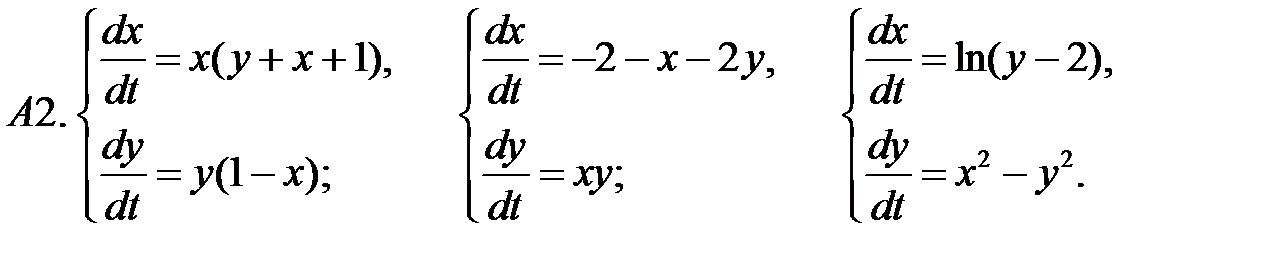
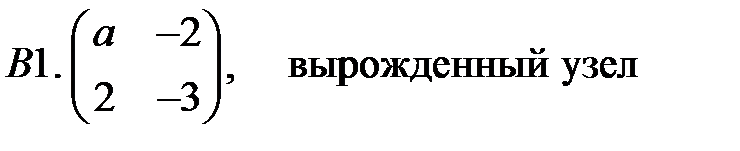 .
. 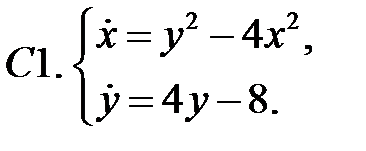
3. А1. 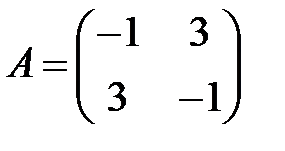 ;
; 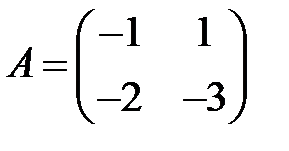 ;
; 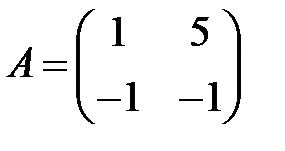 ;
; 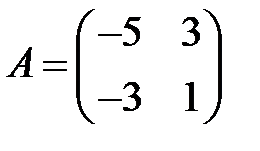 .
.
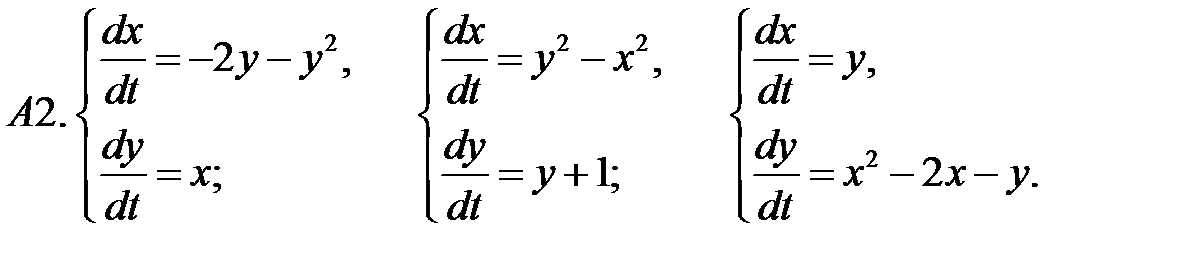
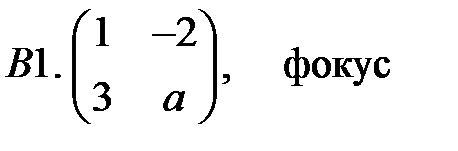 .
. 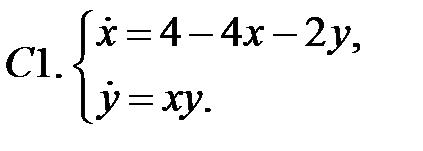
4. А1. 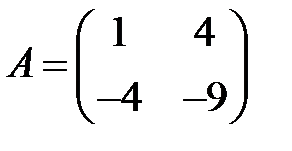 ;
; 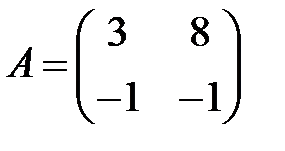 ;
; 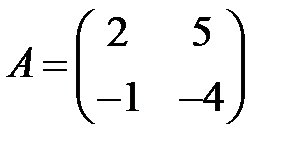 ;
; 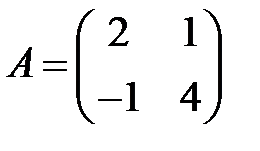 .
.
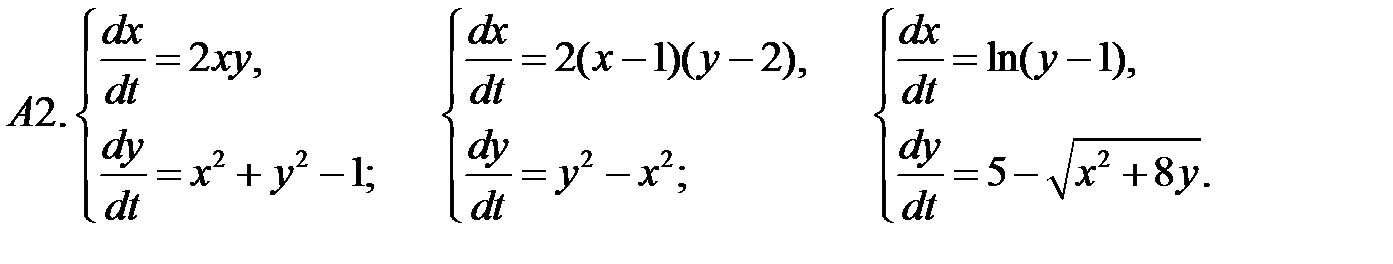
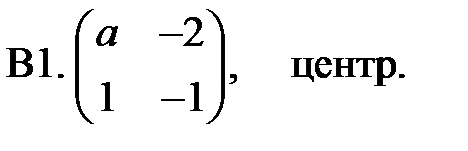
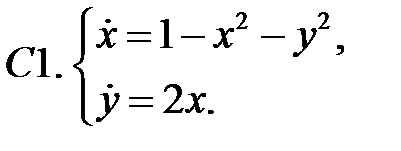
5. А1. 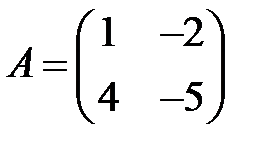 ;
; 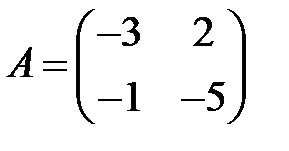 ;
; 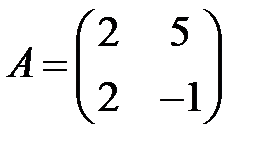 ;
; 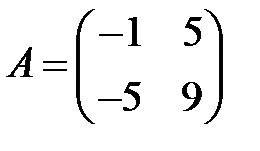 .
.
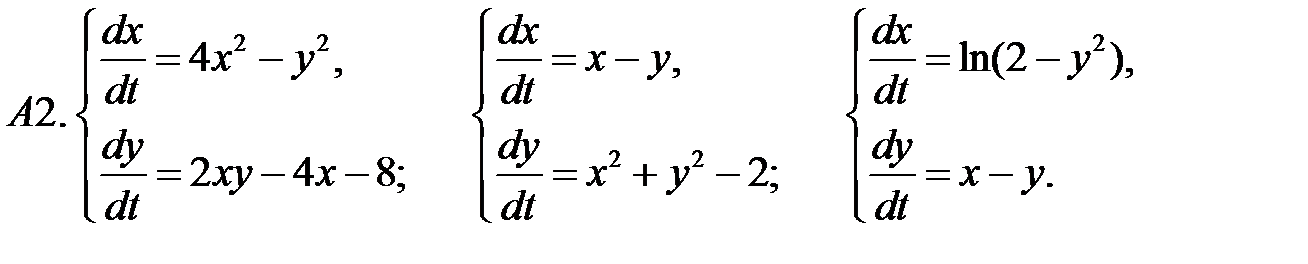
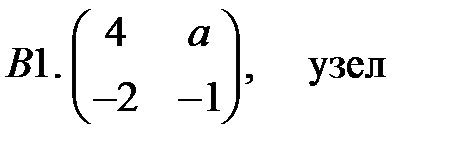 .
. 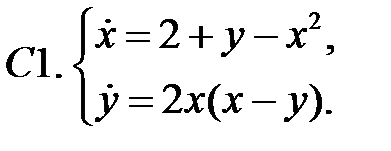
6. А1. 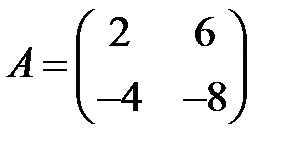 ;
; 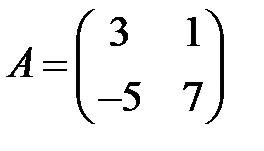 ;
; 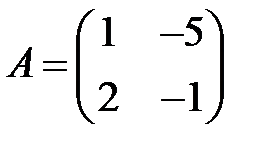 ;
; 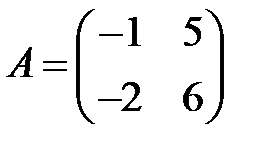 .
.
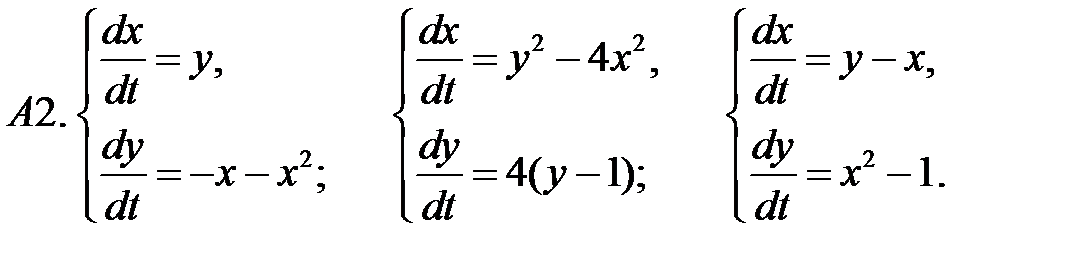
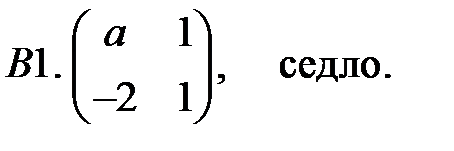
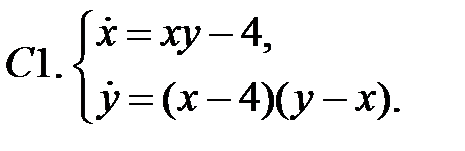
7. А1. 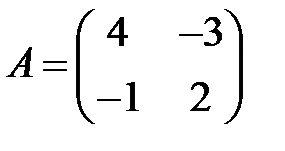 ;
; 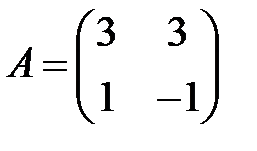 ;
; 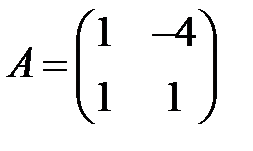 ;
; 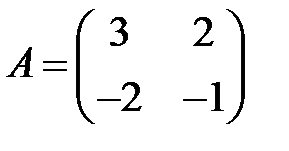 .
.
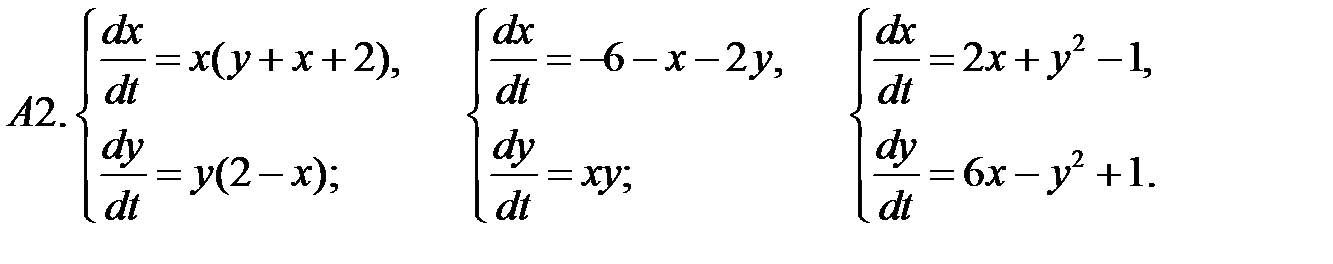
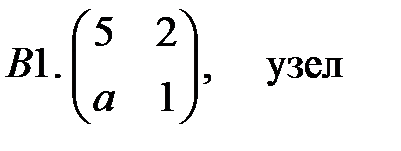 .
. 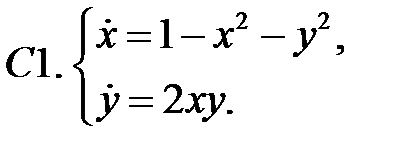
8. А1. 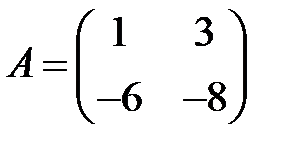 ;
; 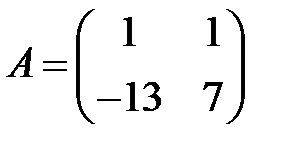 ;
; 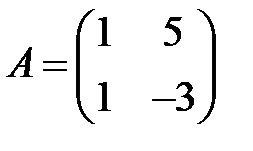 ;
; 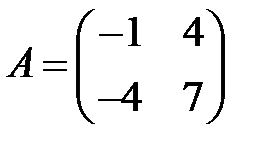 .
.
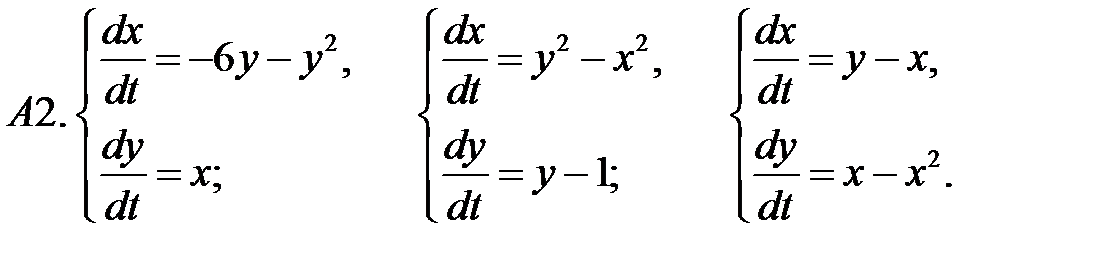
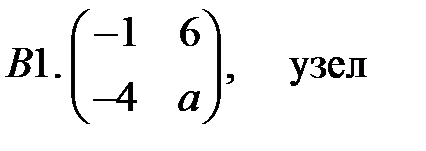 .
. 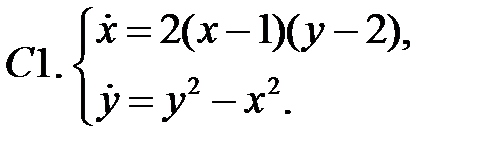
9. А1. 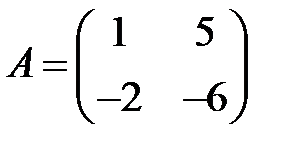 ;
; 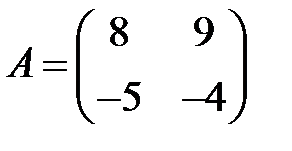 ;
; 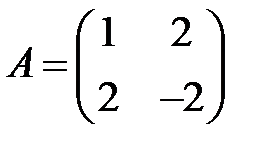 ;
; 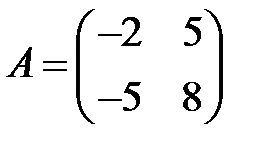 .
.
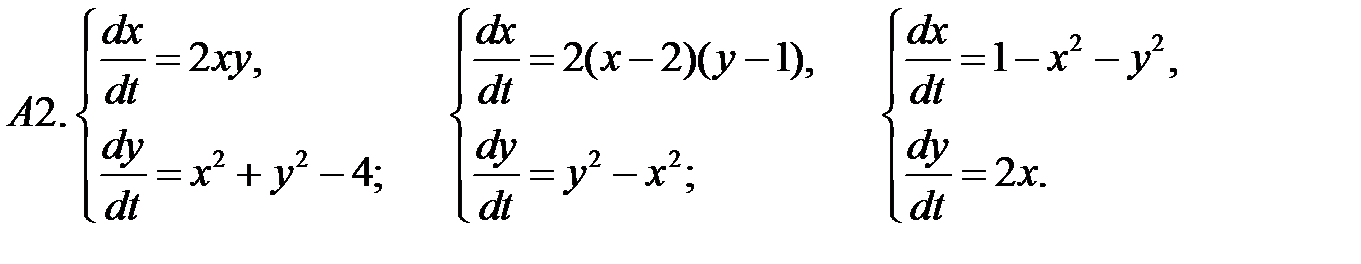
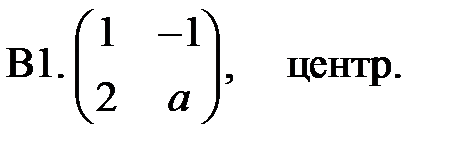
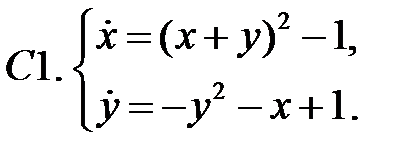
10. А1. 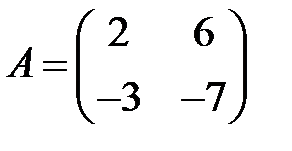 ;
; 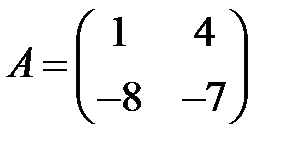 ;
; 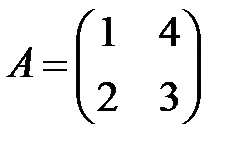 ;
; 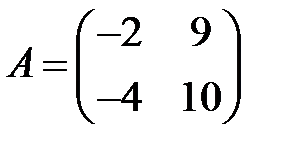 .
.
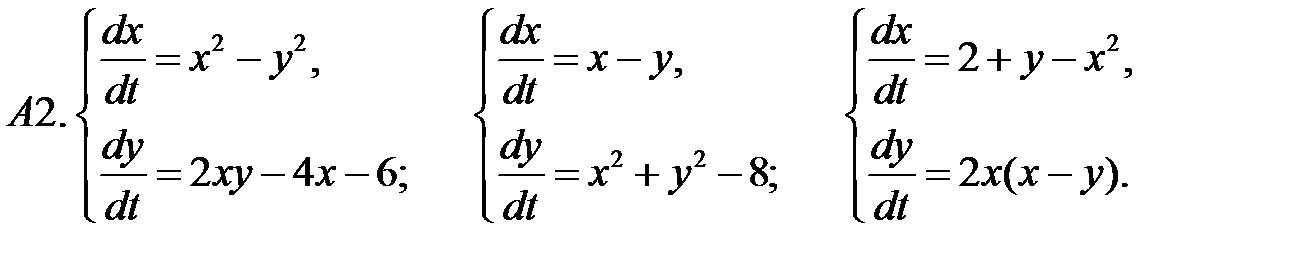
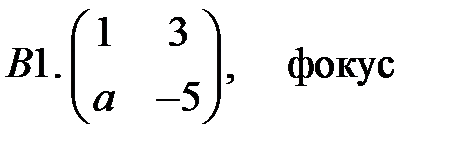 .
. 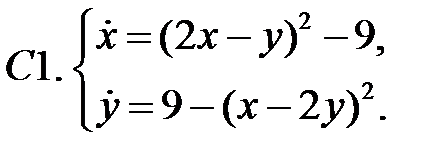
11. А1. 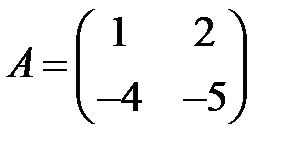 ;
; 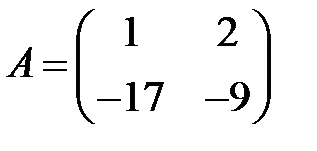 ;
; 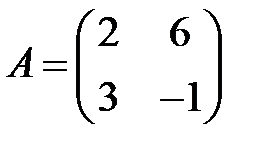 ;
; 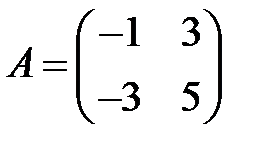 .
.
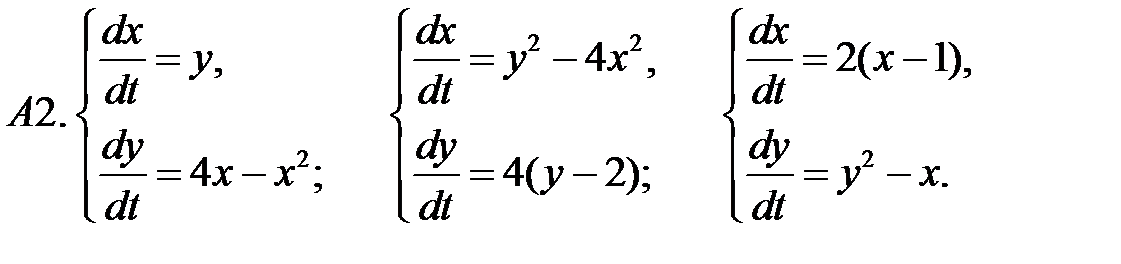
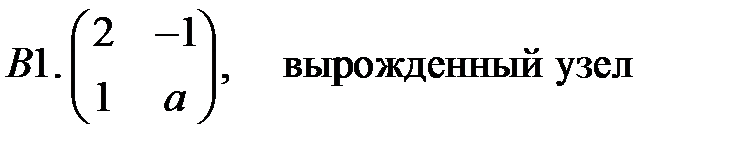 .
. 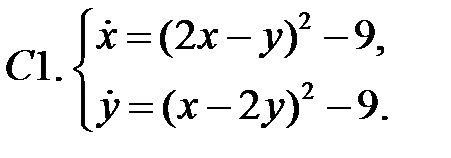
12. А1. 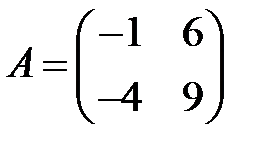 ;
; 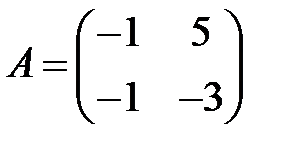 ;
; 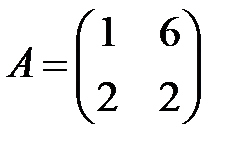 ;
; 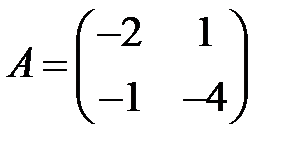 .
.
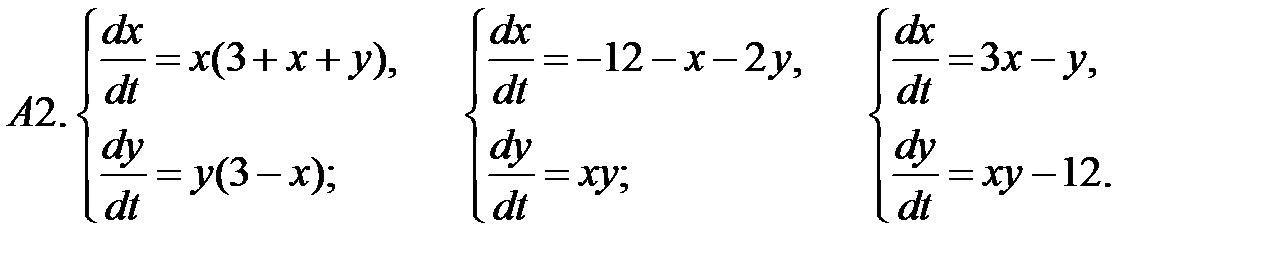
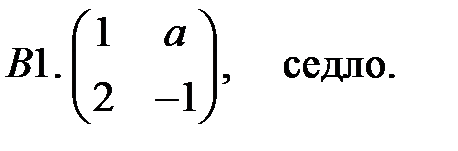
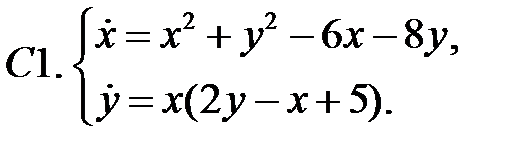
13. А1. 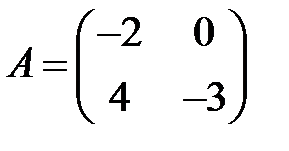 ;
; 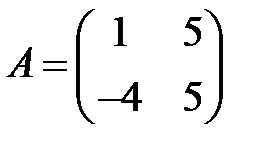 ;
; 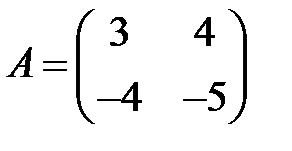 ;
; 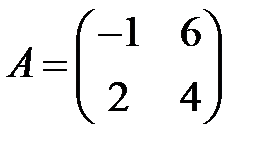 .
.
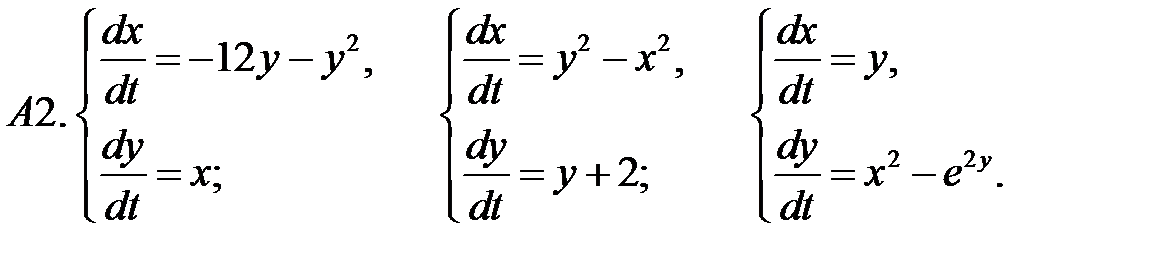
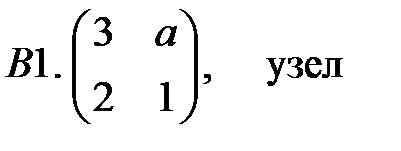 .
. 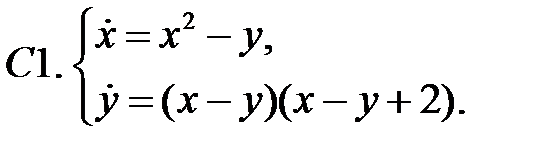
14. А1. 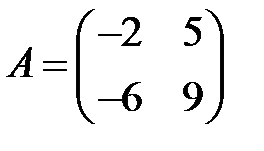 ;
; 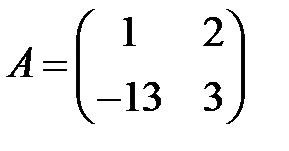 ;
; 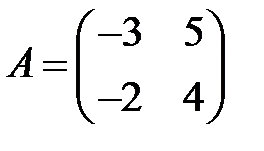 ;
; 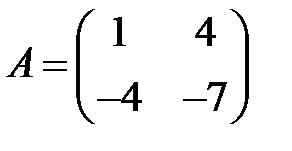 .
.
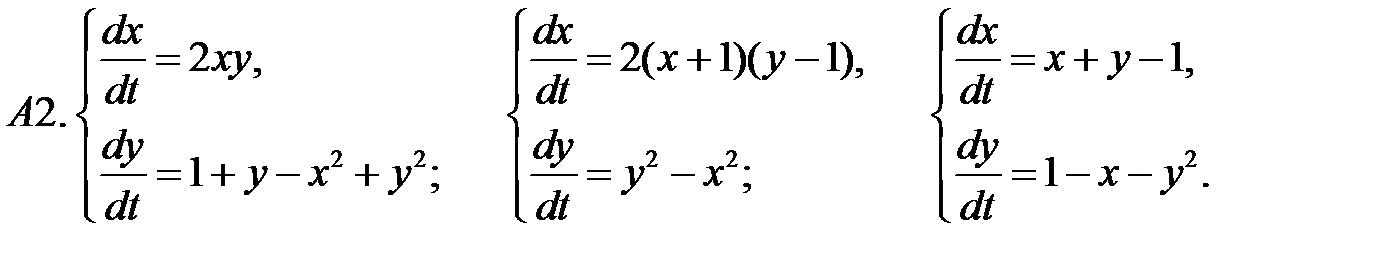
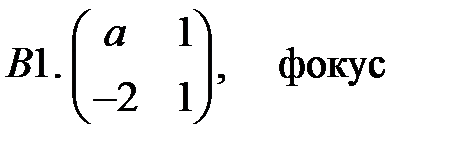 .
. 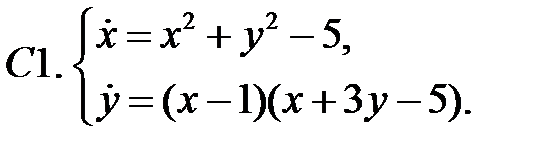
15. А1. 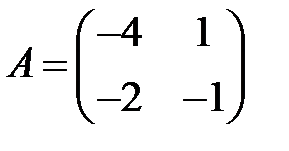 ;
; 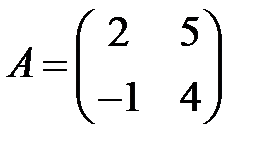 ;
; 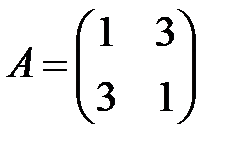 ;
; 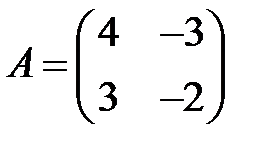 .
.
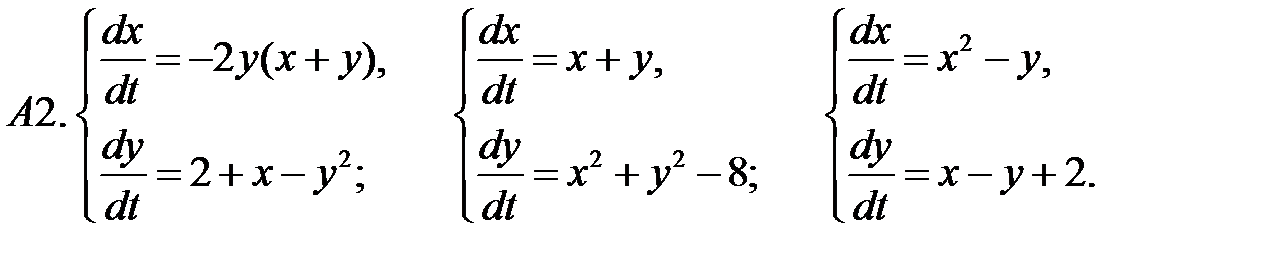
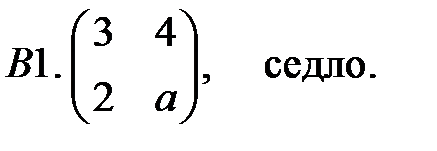
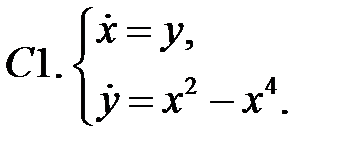
16. А1. 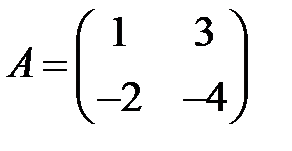 ;
; 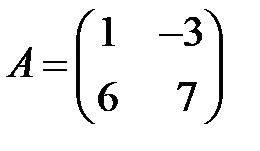 ;
; 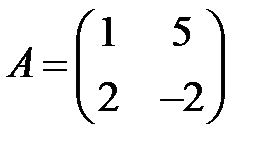 ;
; 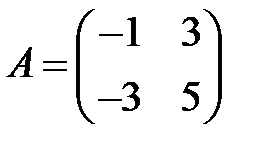 .
.
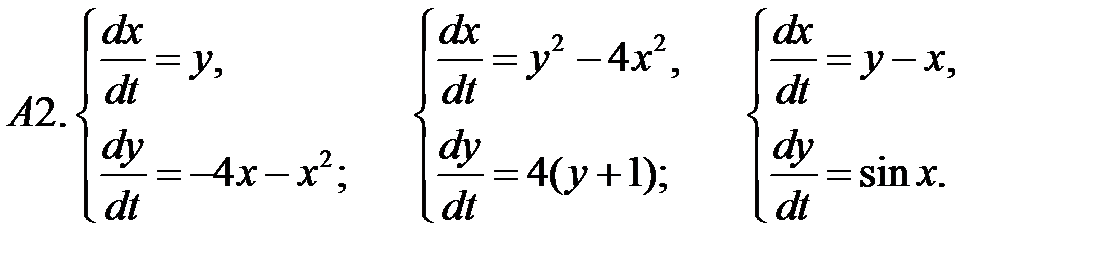
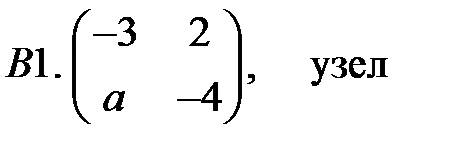 .
. 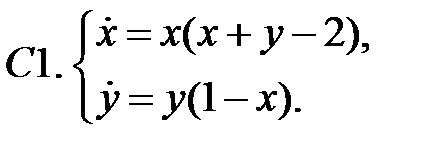
17. А1. 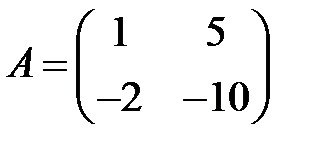 ;
; 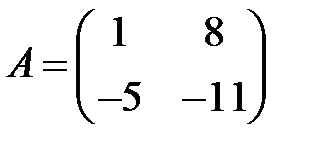 ;
; 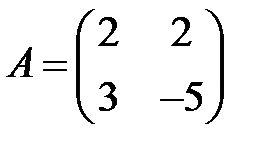 ;
; 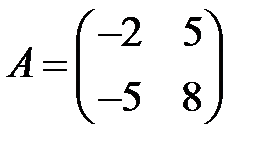 .
.
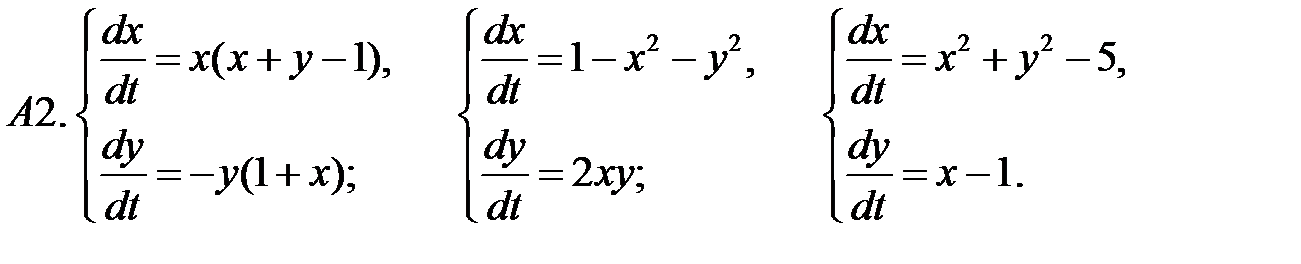
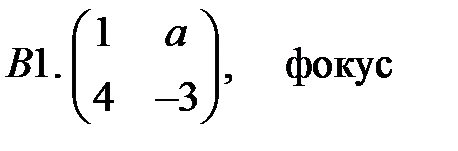 .
. 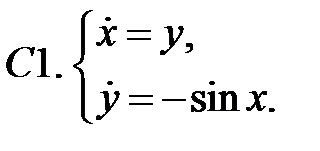
18. А1. 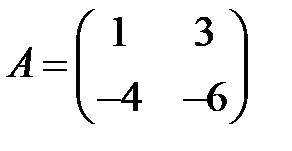 ;
; 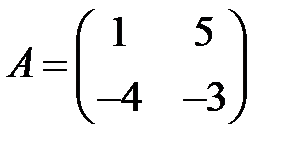 ;
; 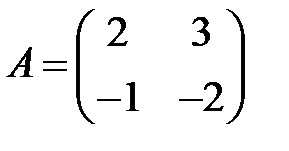 ;
; 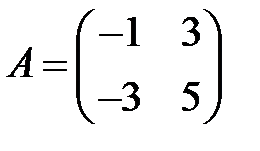 .
.
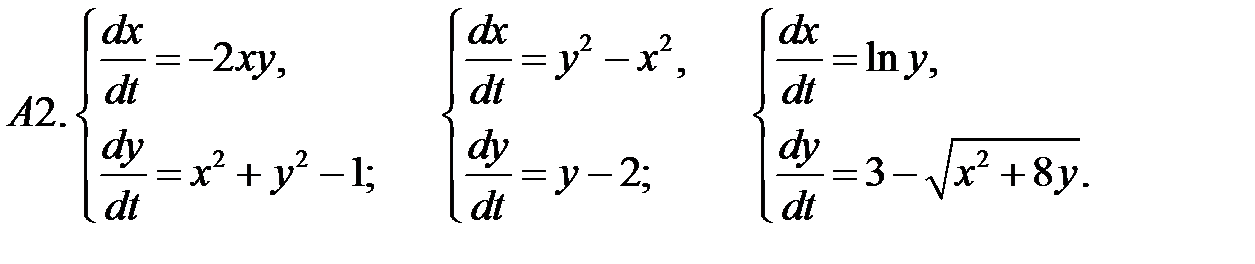
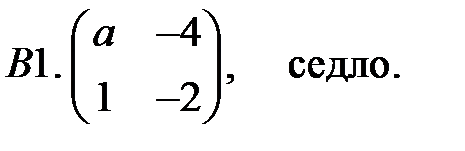
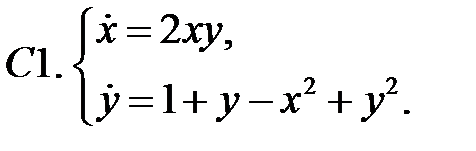
19. А1. 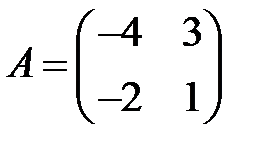 ;
; 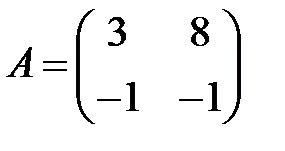 ;
; 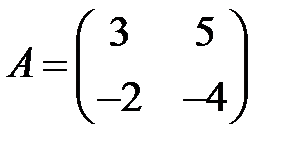 ;
; 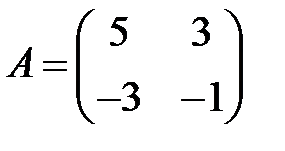 .
.
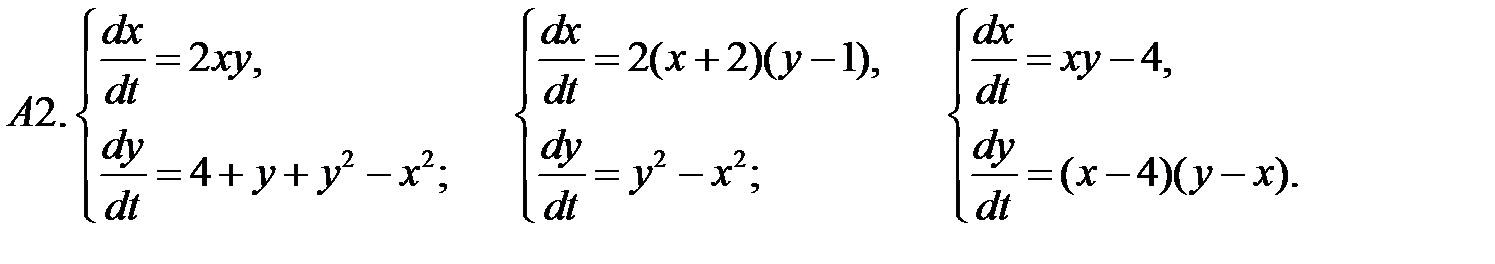
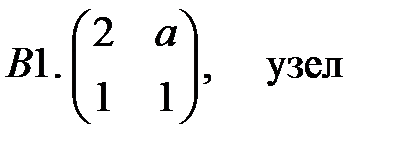 .
. 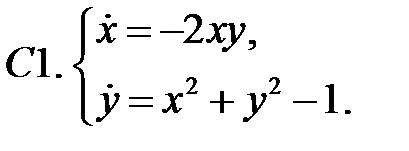
20. А1. 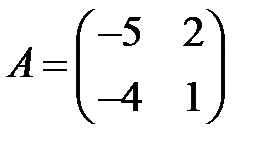 ;
; 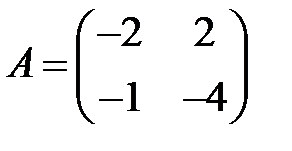 ;
; 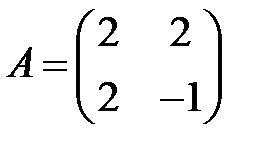 ;
; 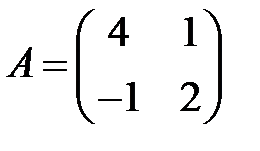 .
.
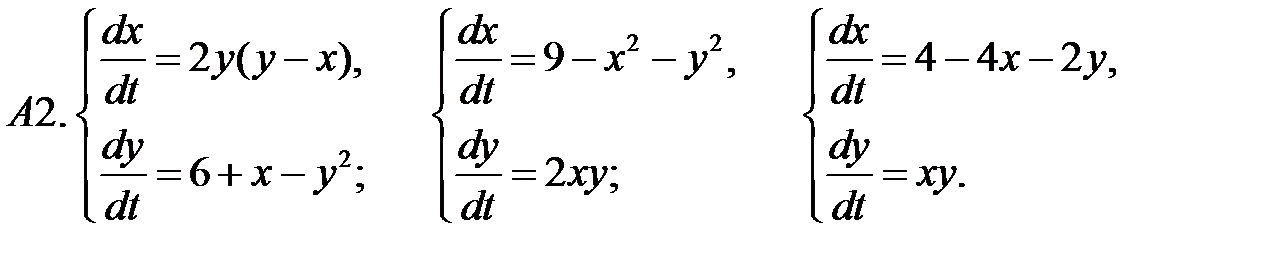
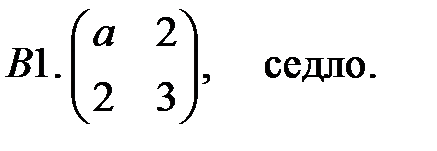
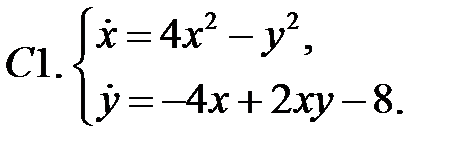
21. А1. 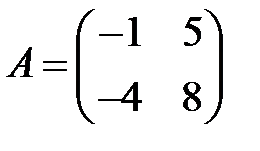 ;
; 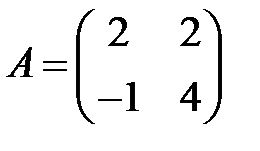 ;
; 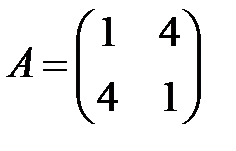 ;
; 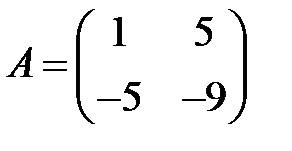 .
.
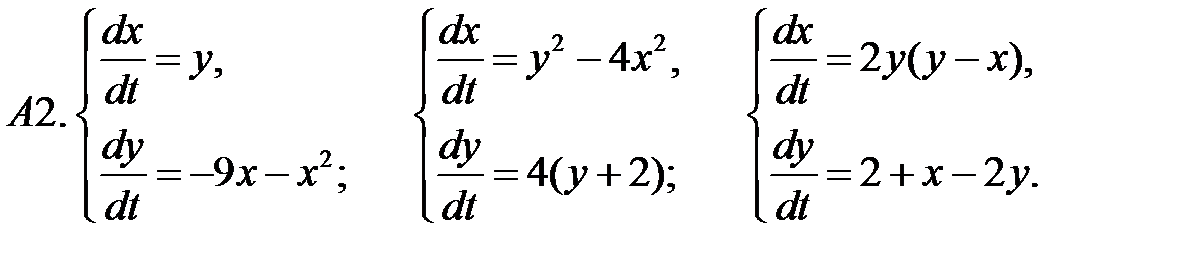
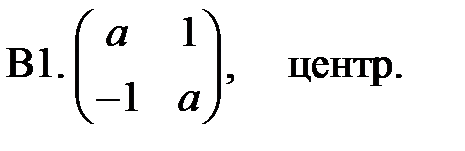
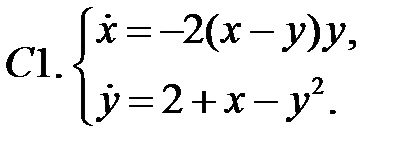
22. А1. 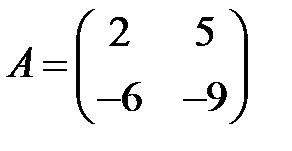 ;
; 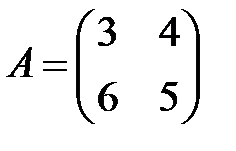 ;
; 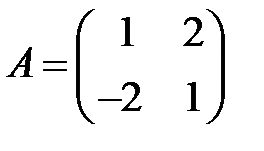 ;
; 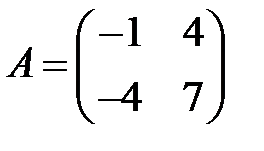 .
.
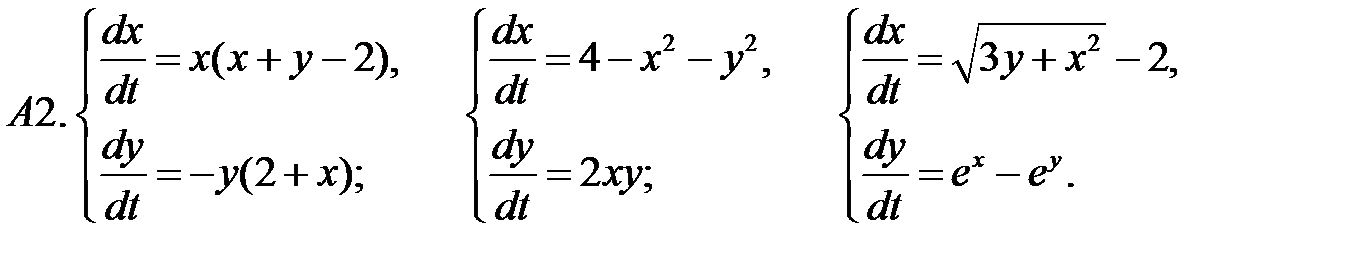
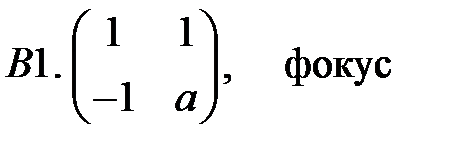 .
. 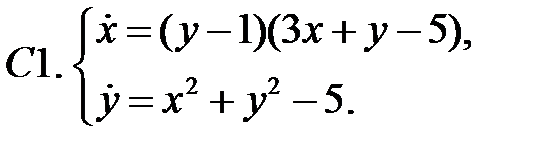
23. А1. 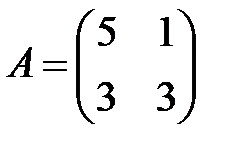 ;
; 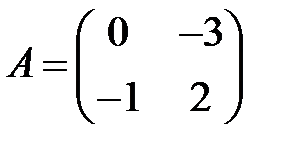 ;
; 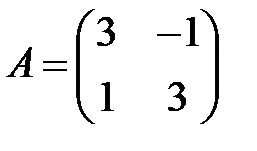 ;
; 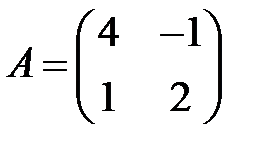 .
.
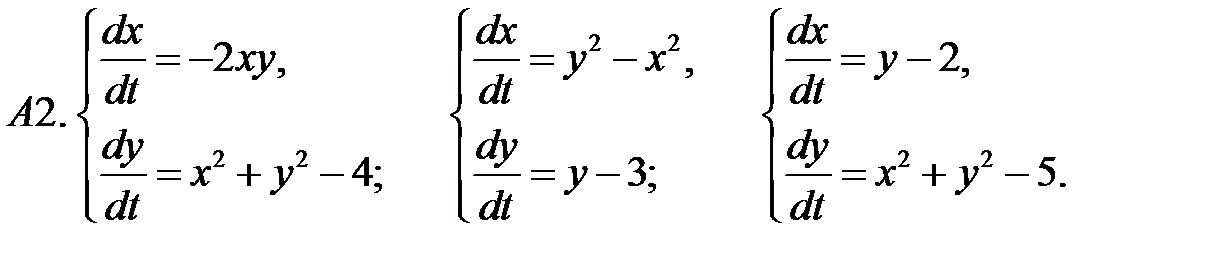
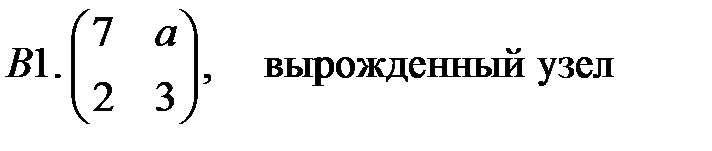 .
. 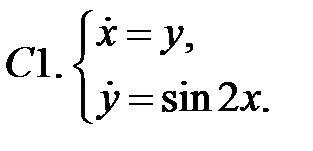
24. А1. 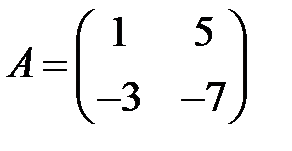 ;
; 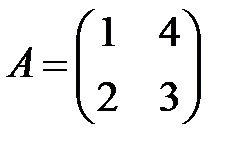 ;
; 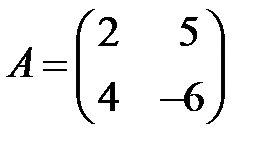 ;
; 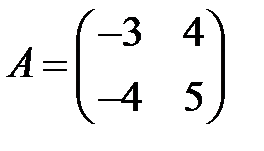 .
.
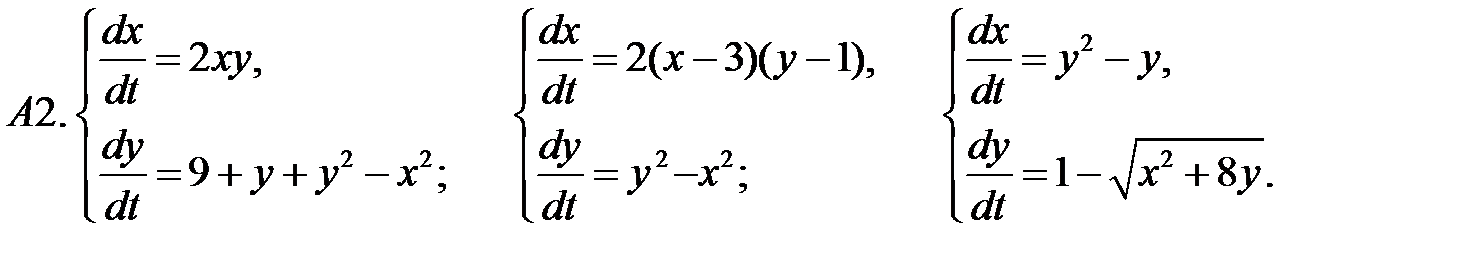
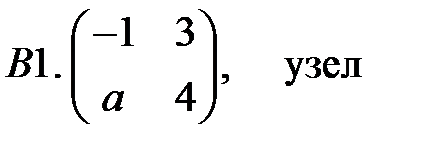 .
. 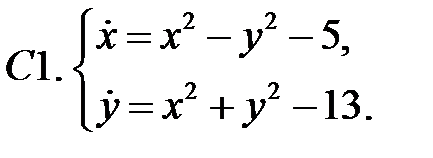
25. А1. 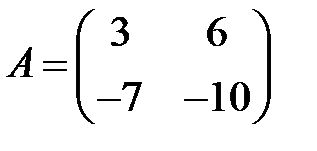 ;
; 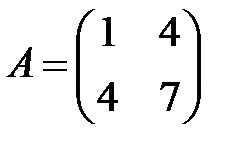 ;
; 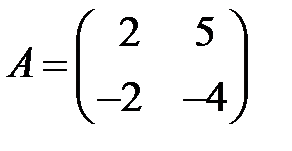 ;
; 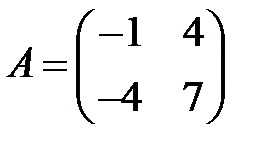 .
.
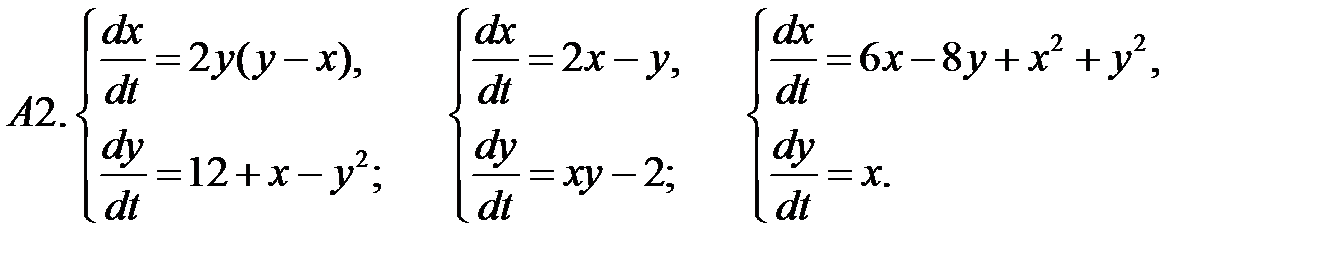
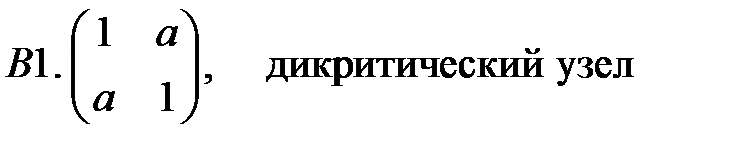 .
. 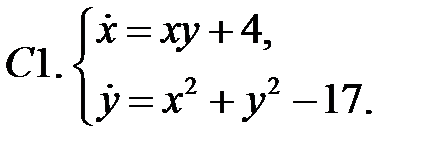
Задание № 28. Устойчивость по Ляпунову
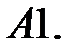 Исследовать устойчивость нулевых решений следующих линейных систем
Исследовать устойчивость нулевых решений следующих линейных систем 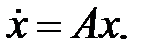
 Исследовать устойчивость нулевого решения систем по первому приближению.
Исследовать устойчивость нулевого решения систем по первому приближению.
 При каких значениях параметров
При каких значениях параметров 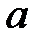 и
и 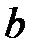 нулевое решение системы асимптотически устойчиво?
нулевое решение системы асимптотически устойчиво?
 Найти все положения равновесия системы и исследовать их на устойчивость.
Найти все положения равновесия системы и исследовать их на устойчивость.
 Исследовать устойчивость нулевого решения системы.
Исследовать устойчивость нулевого решения системы.
 Исследовать устойчивость нулевого решения систем с помощью функции Ляпунова.
Исследовать устойчивость нулевого решения систем с помощью функции Ляпунова.
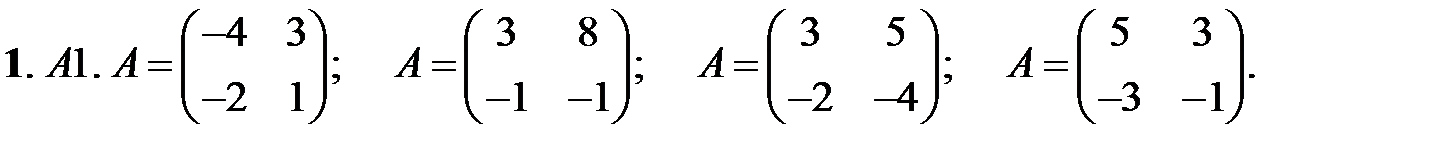
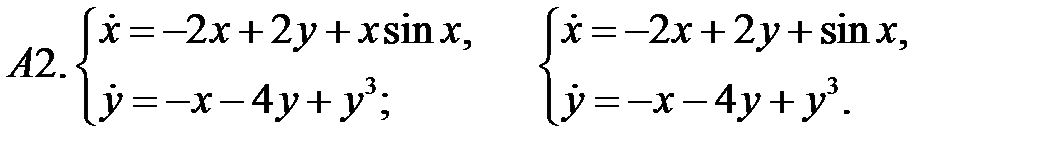
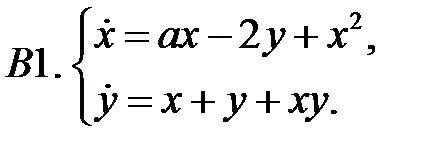
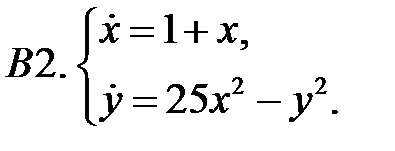
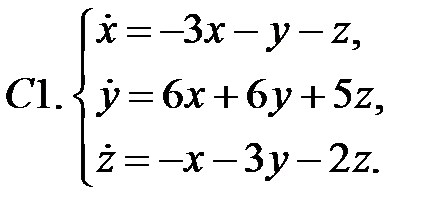
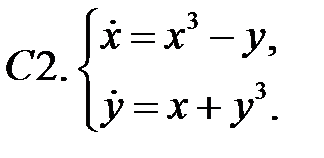
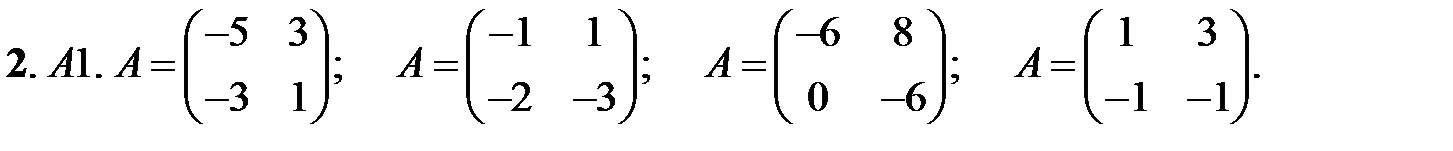
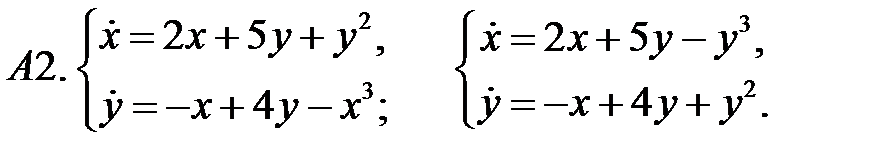
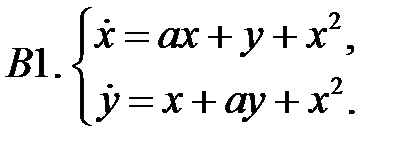
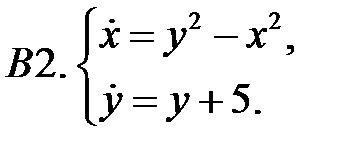
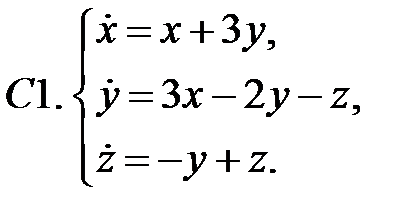
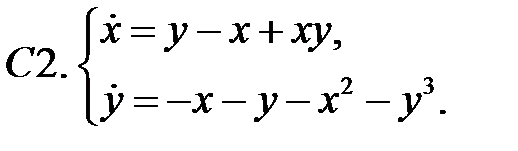
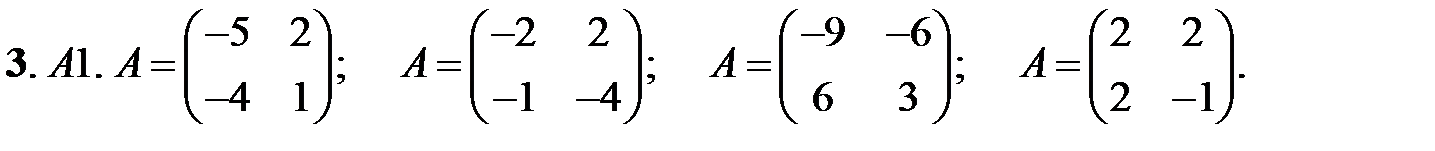
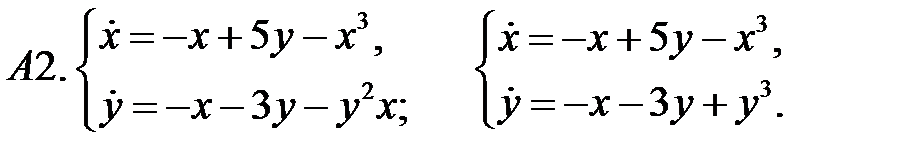
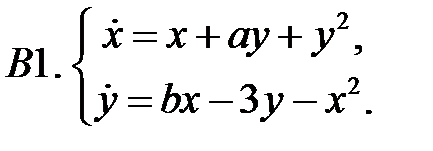
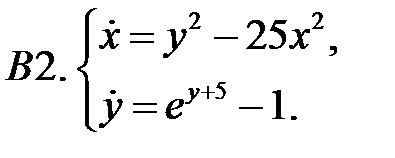
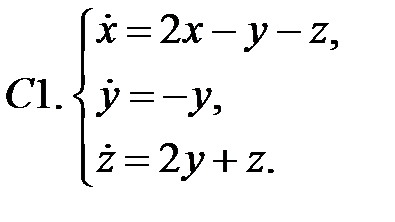
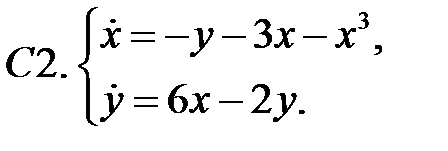
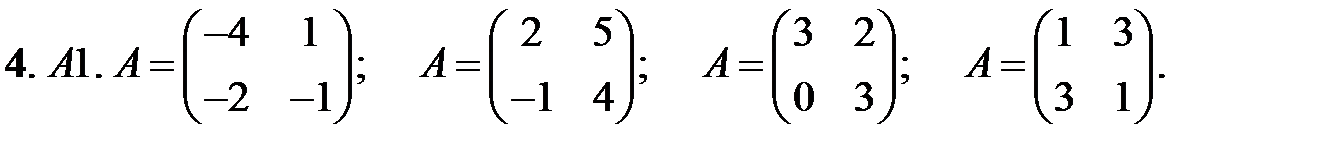
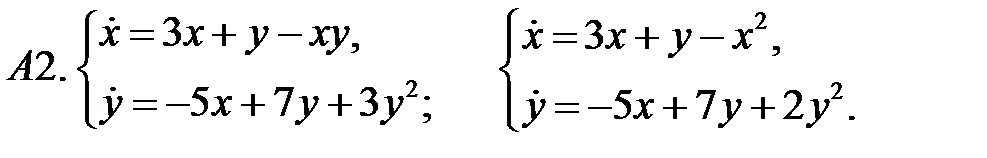
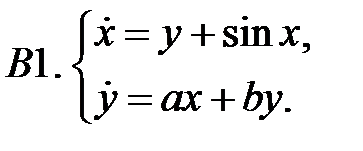
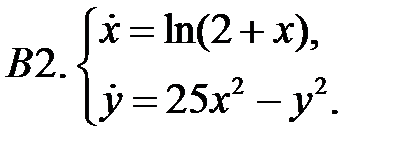
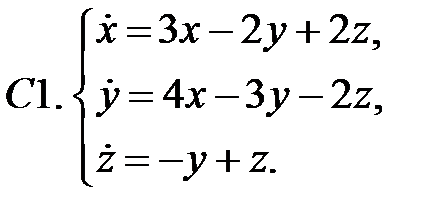
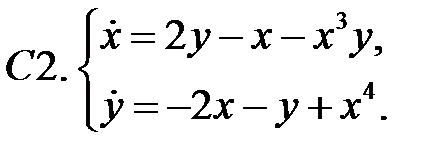

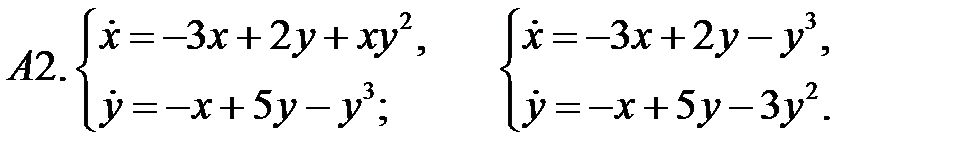
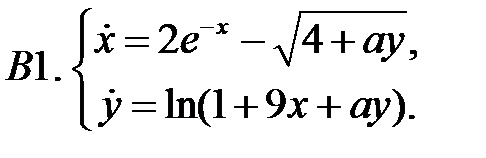
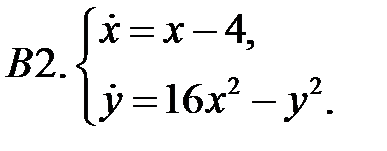
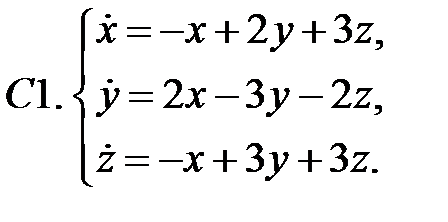
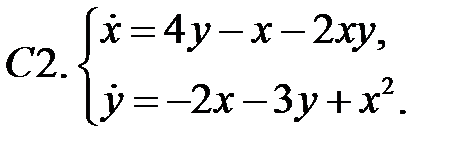
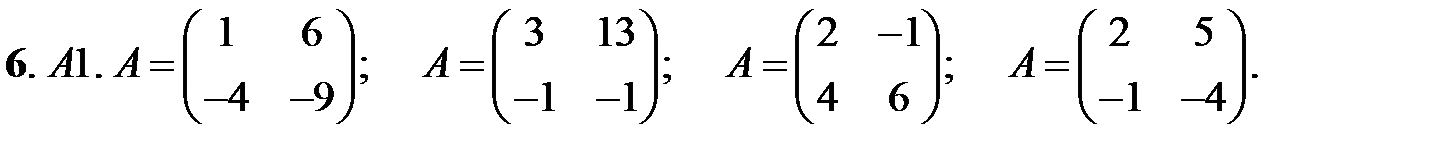
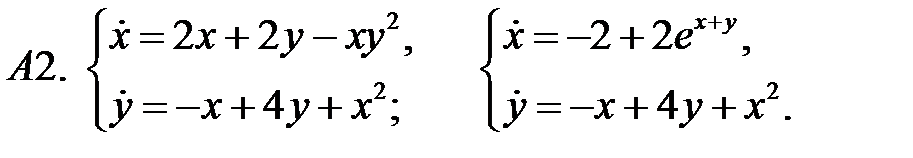
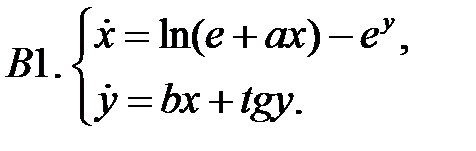
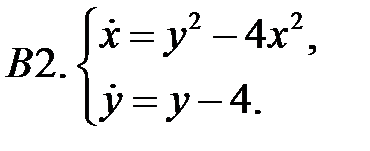
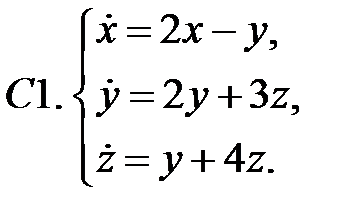
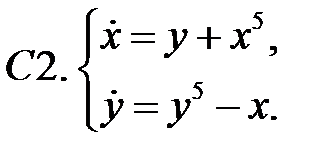
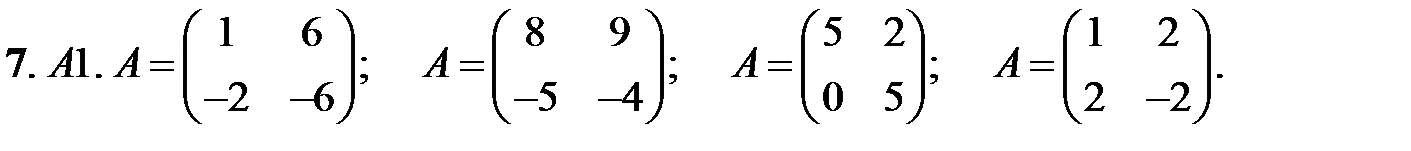
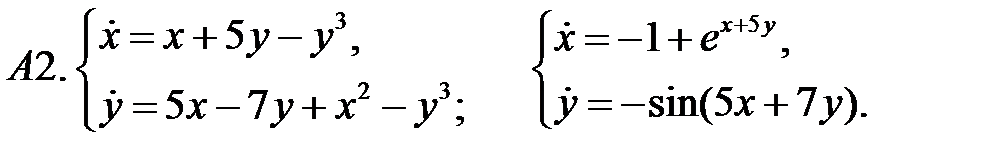
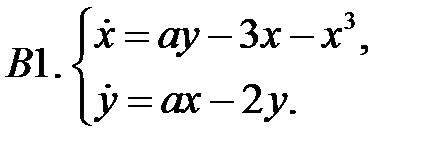
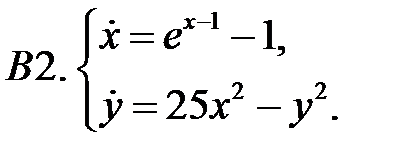
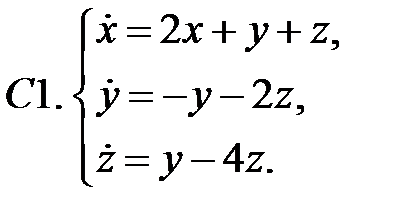
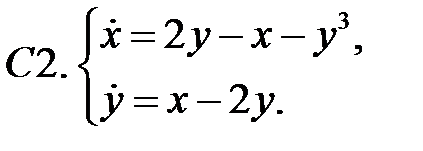
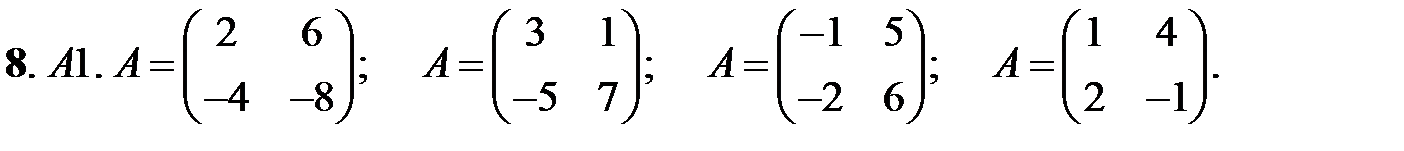
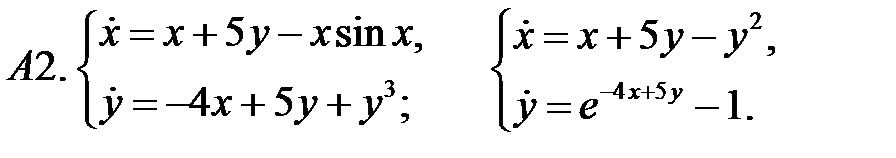
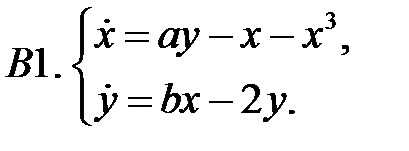
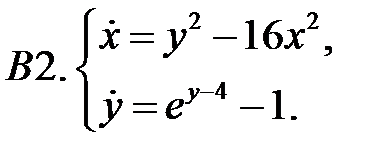
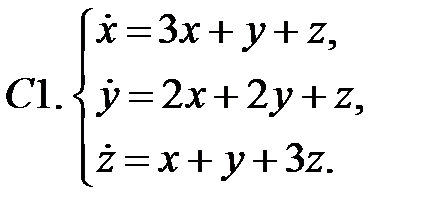
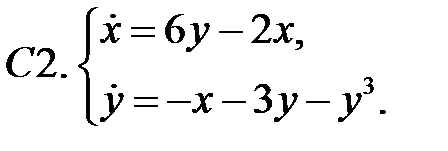
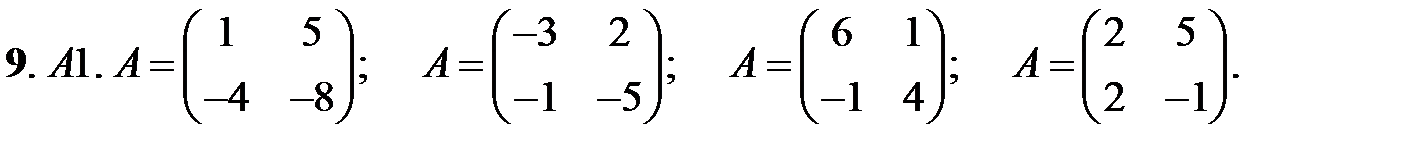
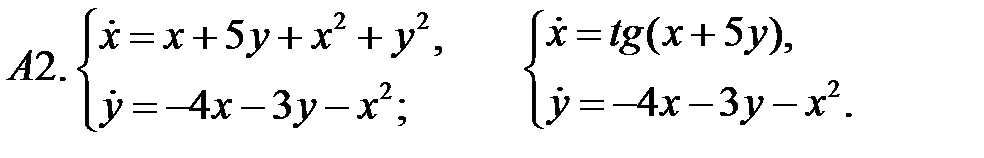
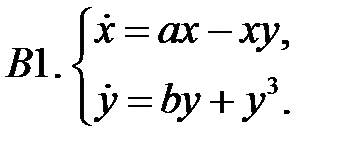
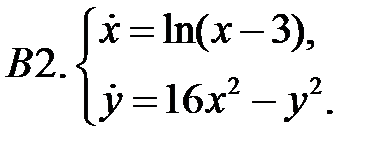
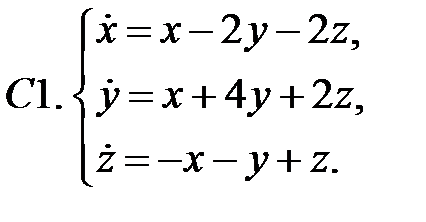
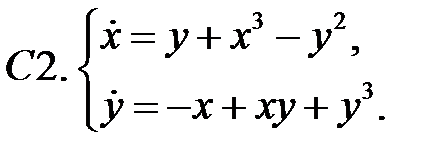
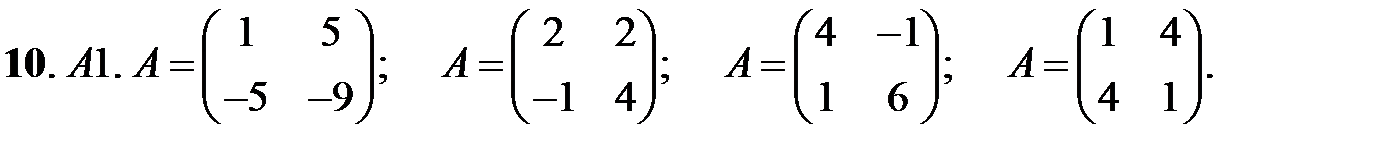
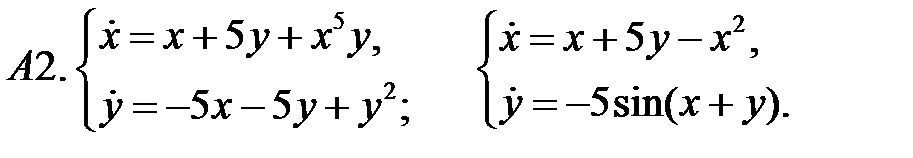
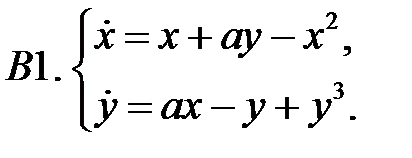
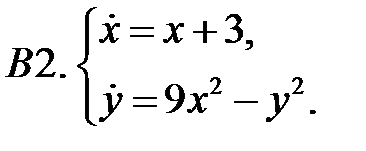
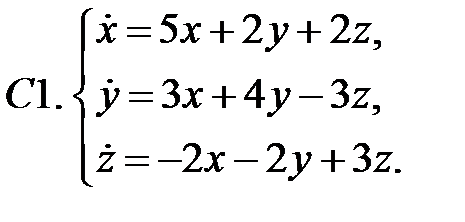
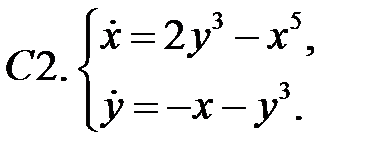
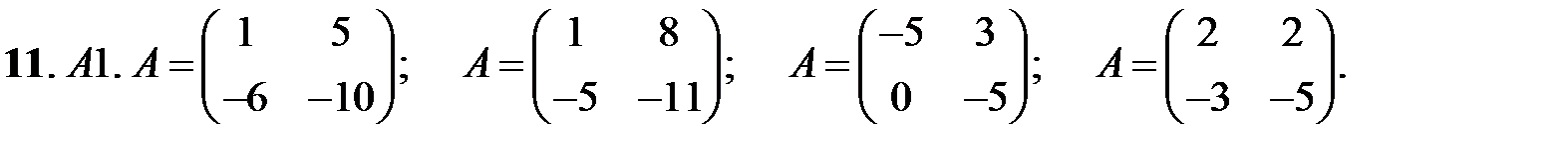
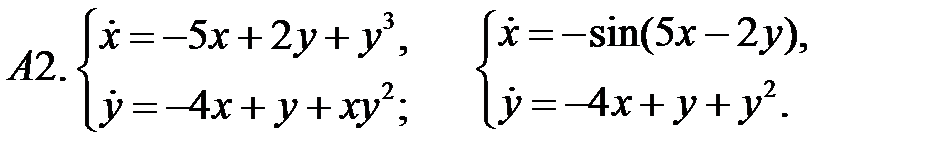
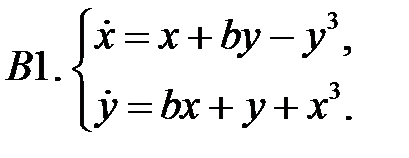
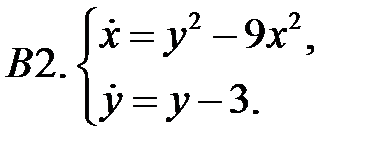
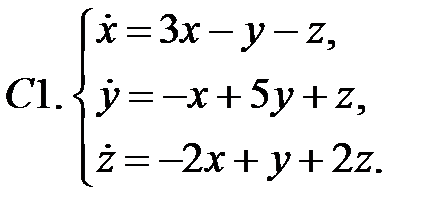
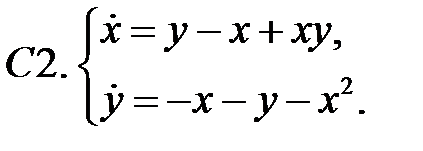
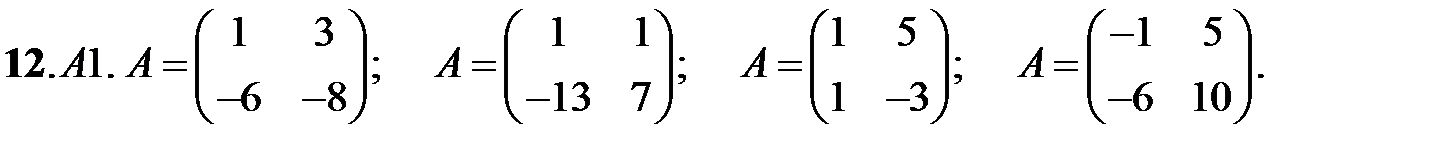
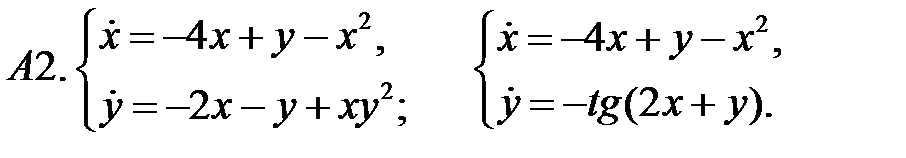
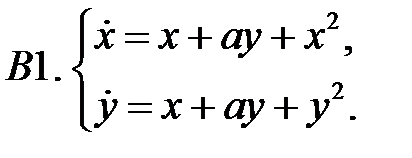
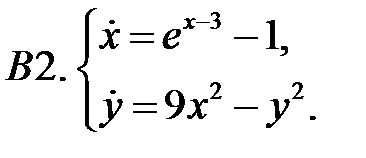
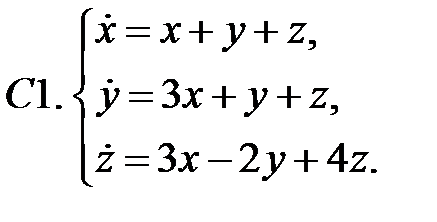
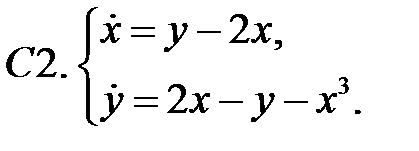
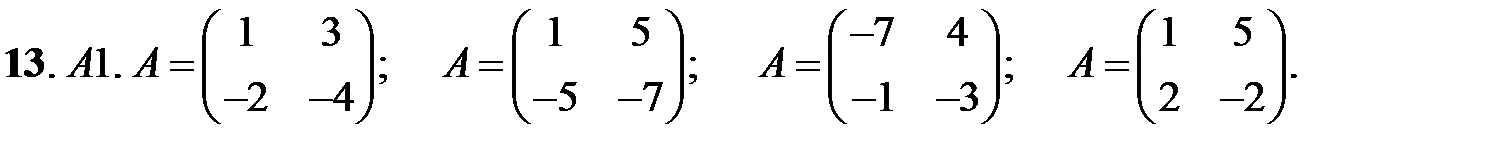
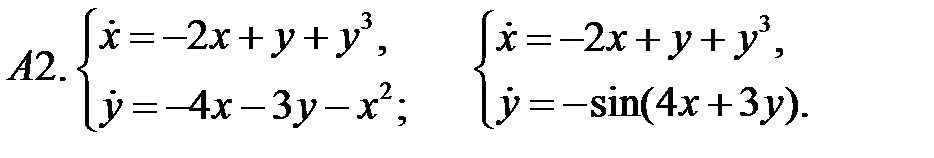
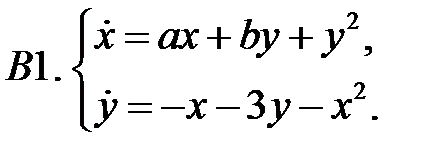
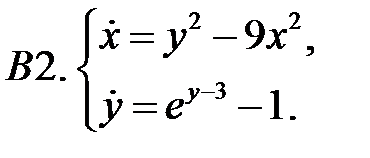
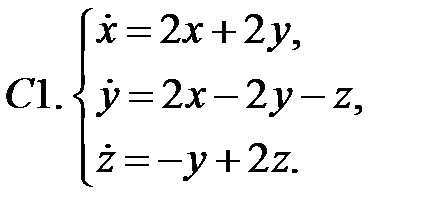
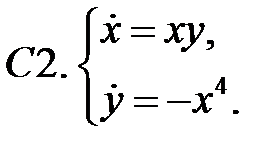
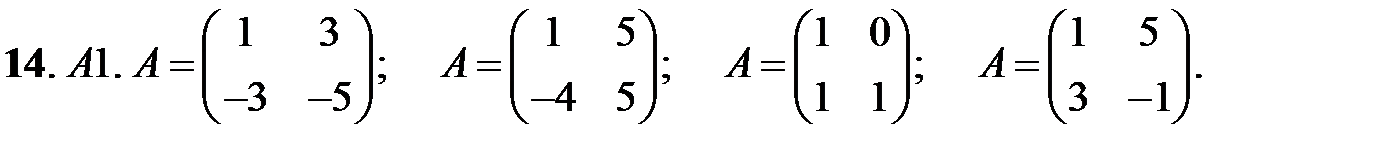
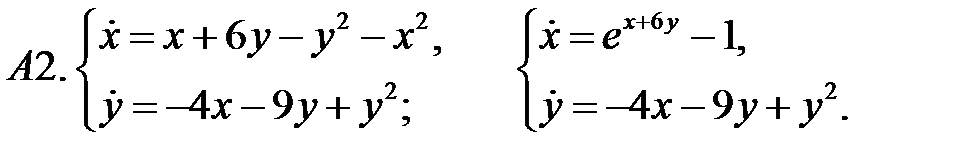
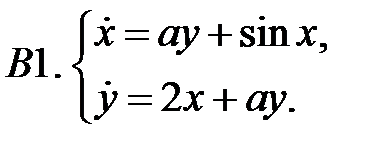
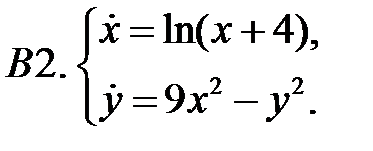
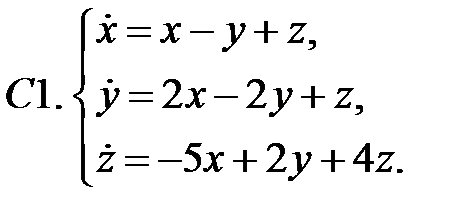
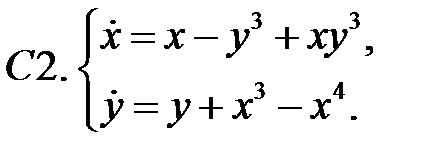
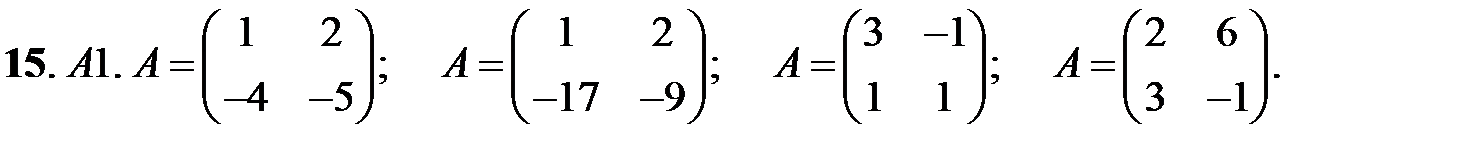
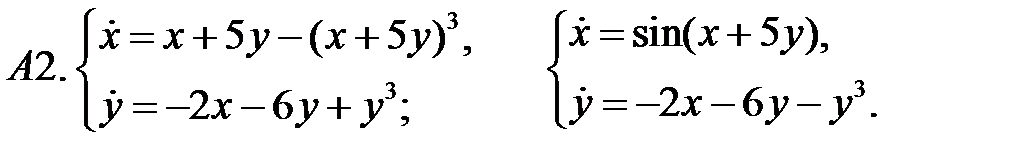
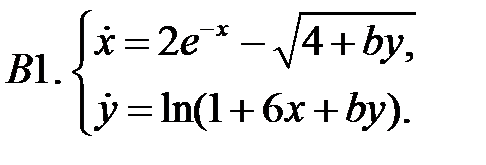
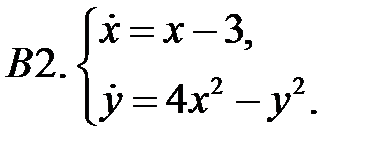
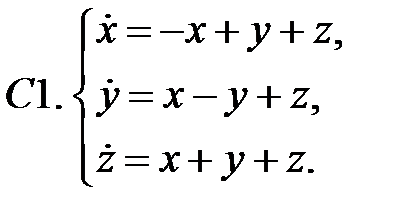
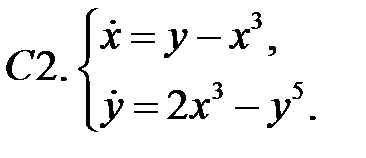
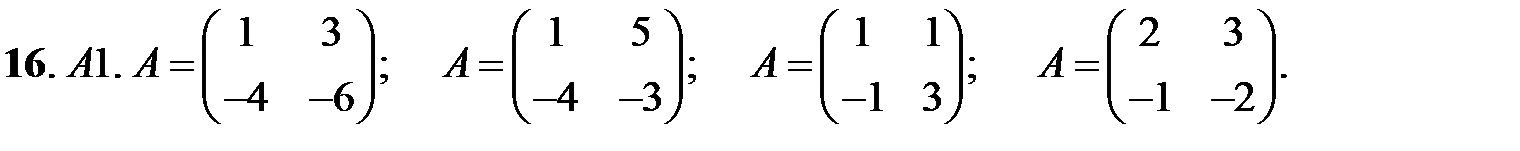
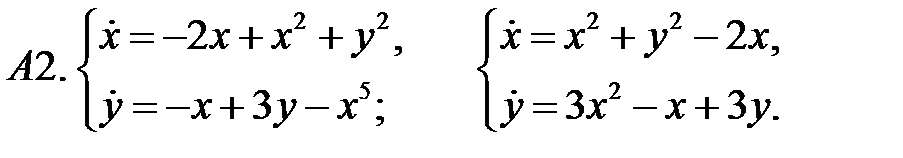
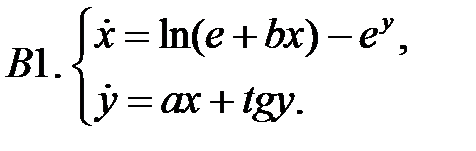
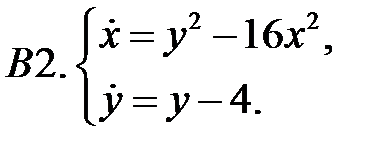
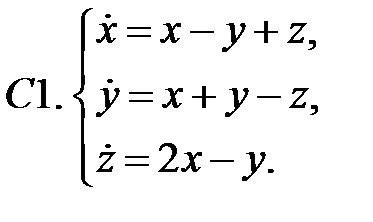
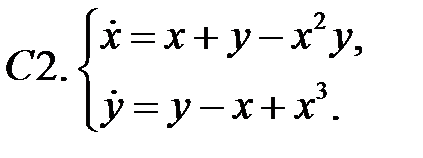
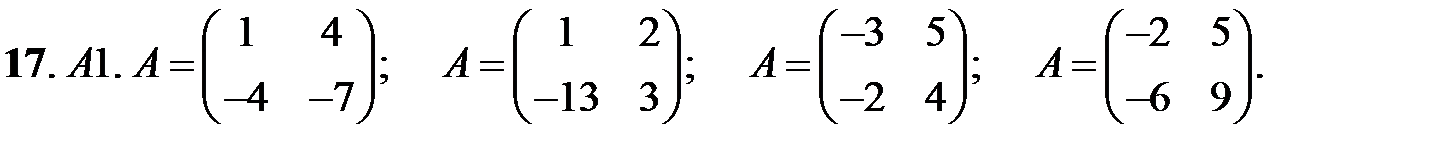
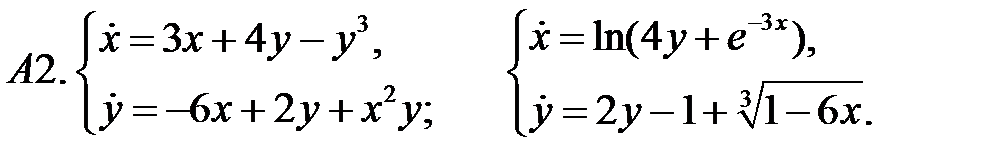
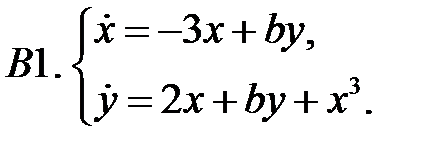
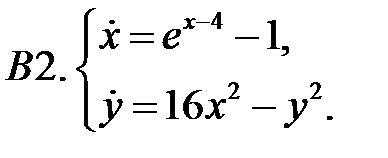
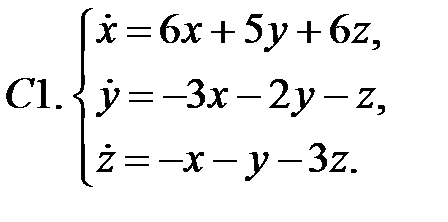
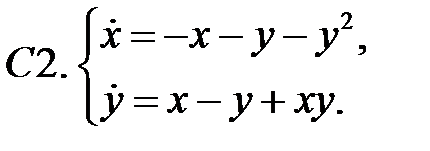
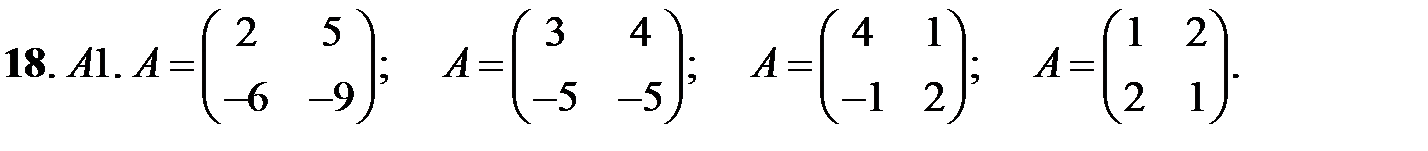
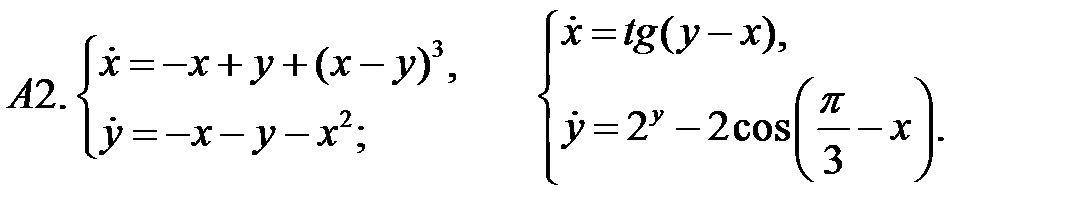
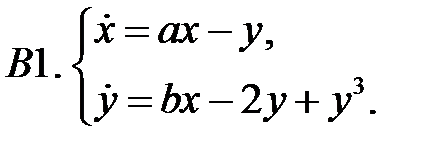
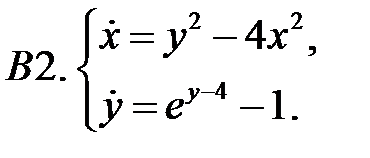
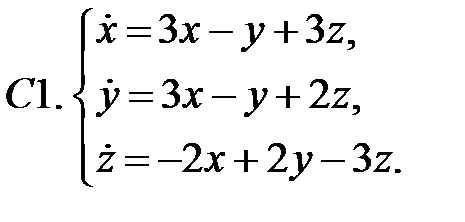
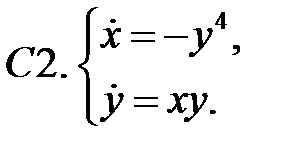
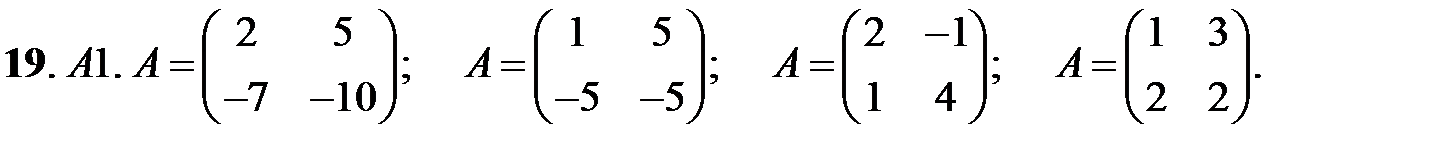
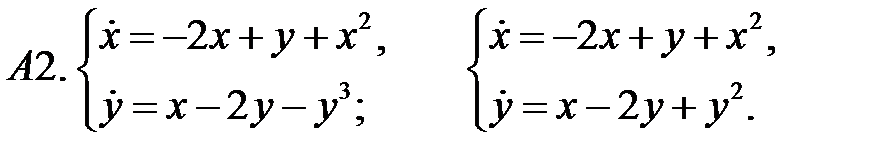
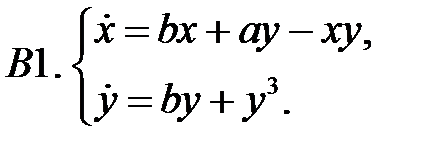
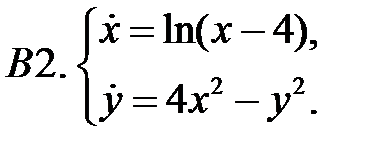
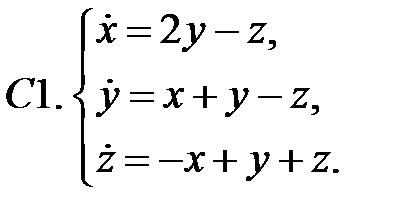
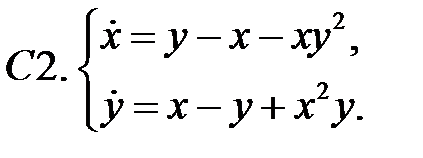
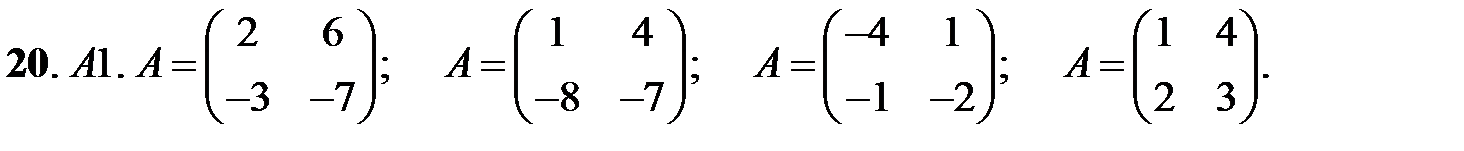
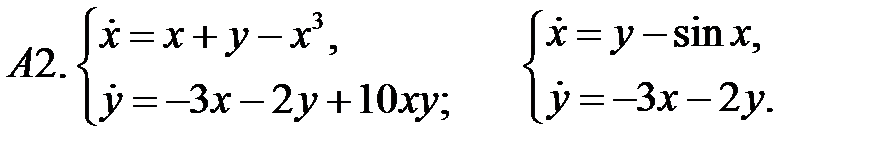
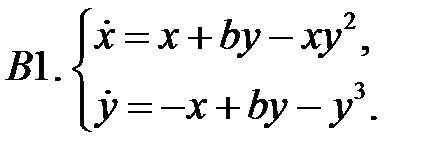
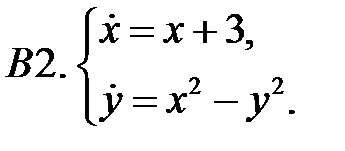
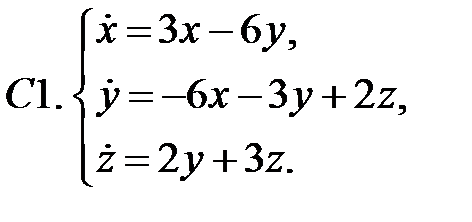
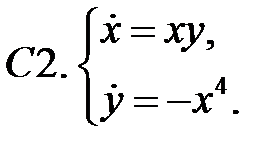
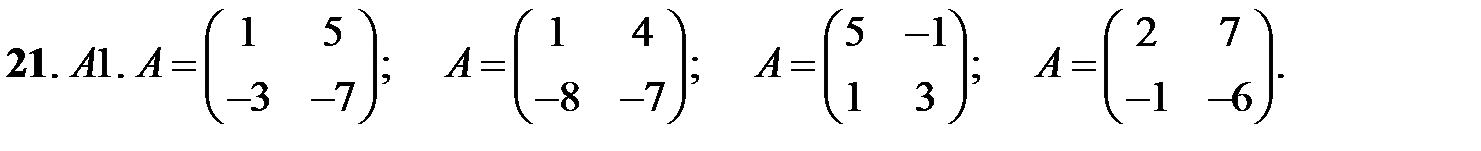
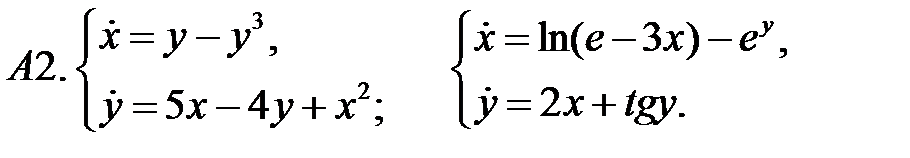
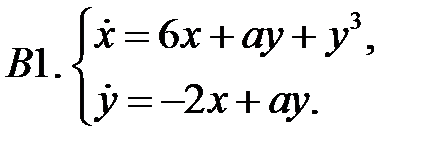
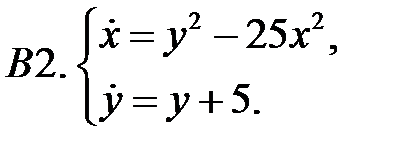
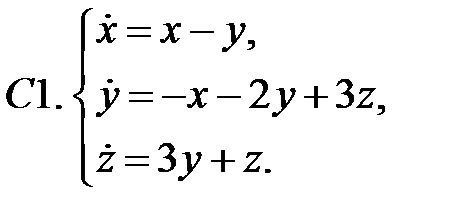
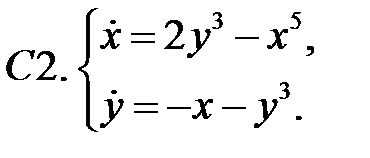
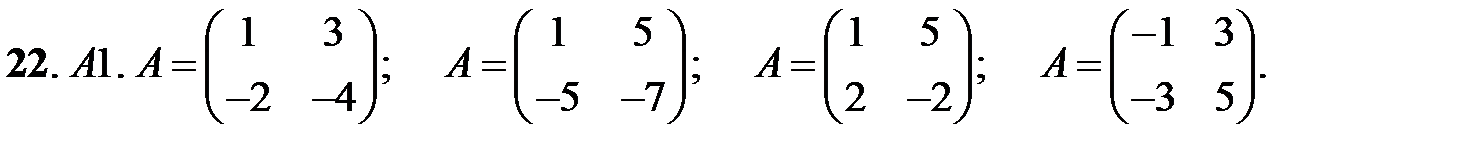
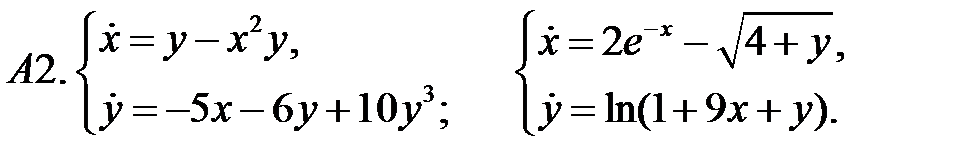
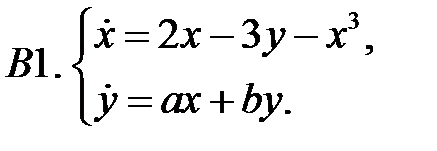
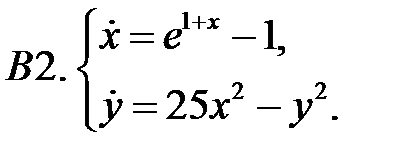
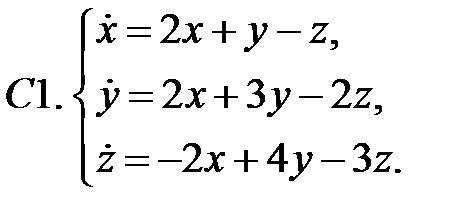
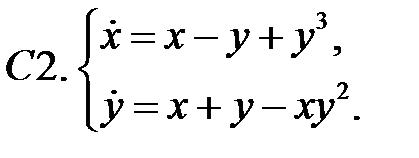
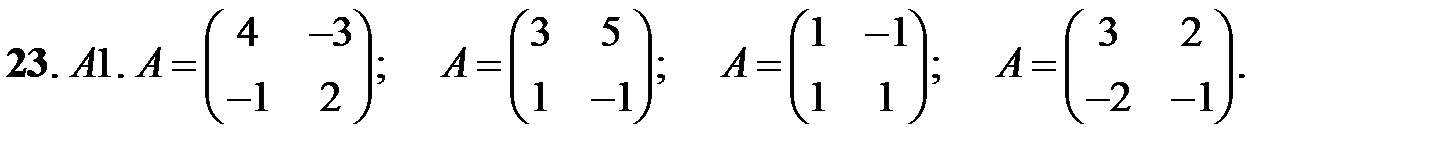
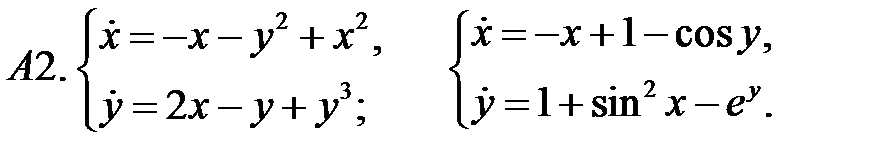
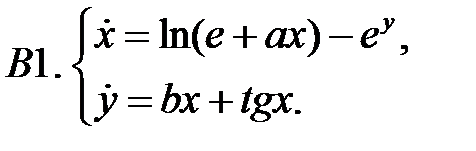
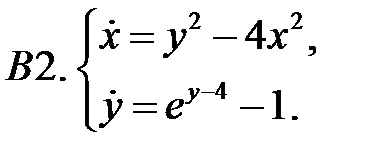
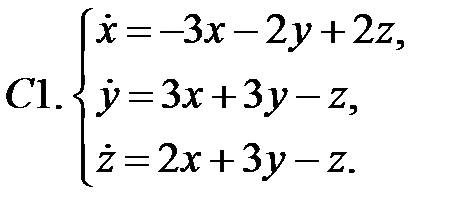
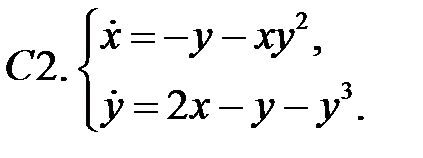
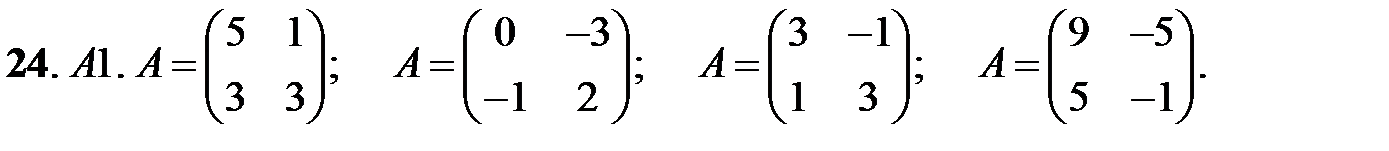
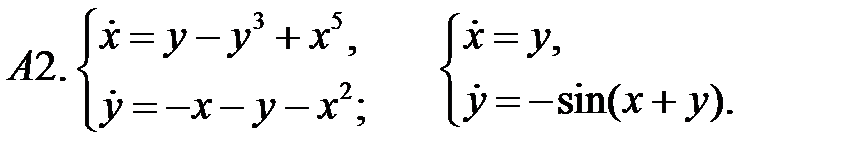
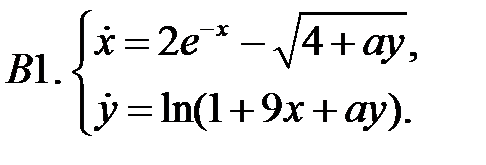
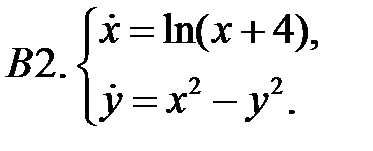
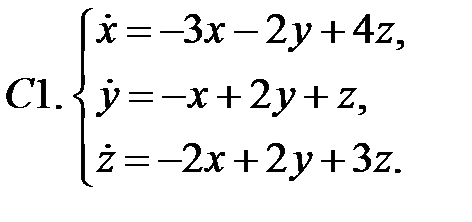
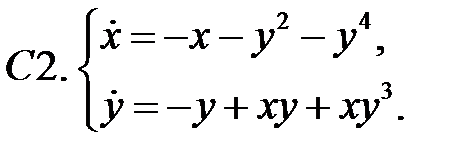
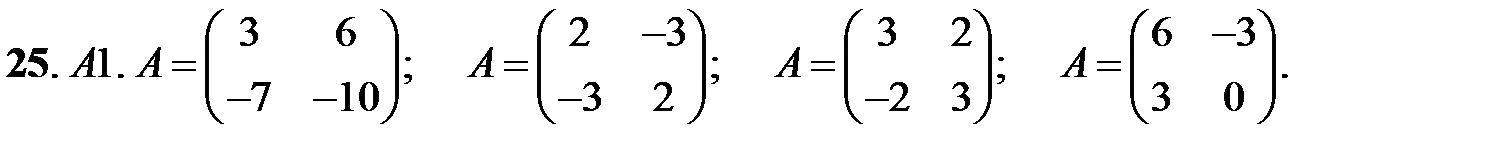
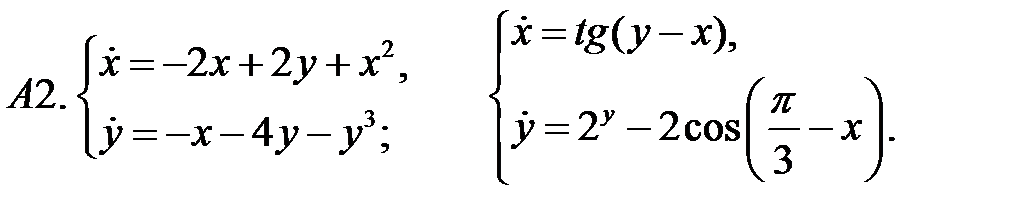
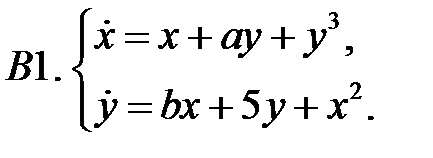
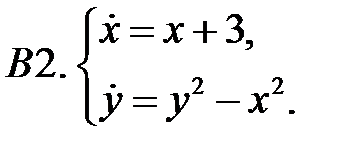
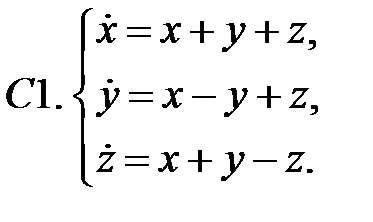
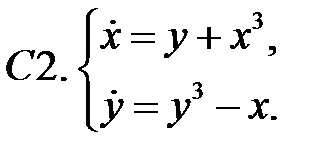
6.7. Вопросы и задачи для повторения
1. Какой общий вид имеет линейная система? Когда она называется однородной, неоднородной?
2. При каком условии задача Коши для линейной системы имеет единственное решение? На каком интервале существуют решения?
3. Всегда ли линейную систему обыкновенных дифференциальных уравнений первого порядка можно преобразовать к эквивалентному линейному обыкновенному дифференциальному уравнению?
4. Почему линейная система не имеет особых решений?
5. Какие решения однородных систем называются линейно независимыми?
6. Что такое фундаментальная система решений? Может ли нулевое решение входить в состав фундаментальных систем решений?
7. Какое условие является необходимым и достаточным для того, чтобы данная система решений была фундаментальной? Сколько фундаментальных систем решений имеет заданная однородная линейная система?
8. Выяснить, являются ли решения
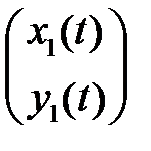 и
и 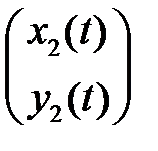
системы уравнений
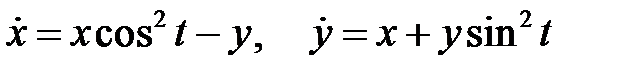
линейно независимыми на 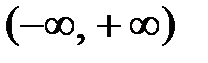 , если известно, что
, если известно, что
а) 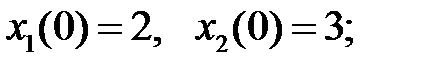 б)
б) 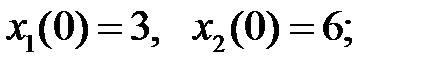
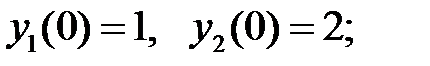
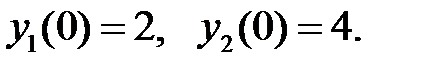
9. Вычислить при 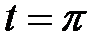 значение определителя Вронского, составленного из решений:
значение определителя Вронского, составленного из решений:
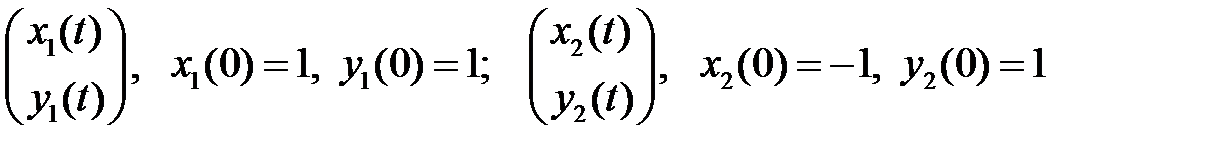 ,
,
системы уравнений
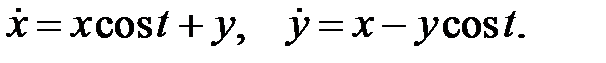
10. Как построить общее решение линейной однородной системы, если известна фундаментальная система решений? В какой области определено общее решение?
11. В чем состоит задача Коши для линейной системы? Как решить задачу Коши при помощи формулы общего решения?
12. Можно ли задачу Коши для линейной системы обыкновенных дифференциальных уравнений первого порядка
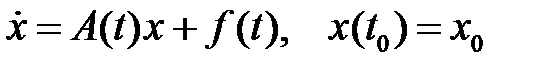
преобразовать эквивалентным образом в задачу Коши с нулевым начальным вектором 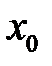 ?
?
13. В каком случае решения задач Коши
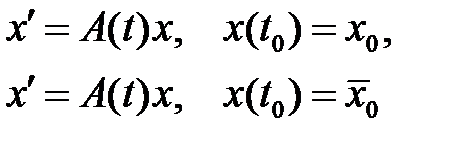
будут линейно независимыми?
14. В каком случае систему обыкновенных дифференциальных уравнений первого порядка 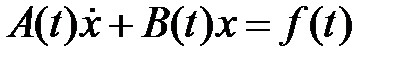 можно преобразовать к системе линейных обыкновенных дифференциальных уравнений первого порядка в нормальном виде?
можно преобразовать к системе линейных обыкновенных дифференциальных уравнений первого порядка в нормальном виде?
15. Можно ли систему линейных дифференциальных уравнений
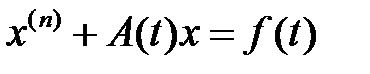
в случае 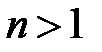 преобразовать к системе линейных обыкновенных дифференциальных уравнений первого порядка?
преобразовать к системе линейных обыкновенных дифференциальных уравнений первого порядка?
16. Как найти общее решение линейной неоднородной системы, если известно одно её частное решение и общее решение соответствующей однородной системы?
17. Можно ли, зная фундаментальную систему решений линейной системы 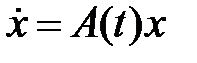 , построить общее решение системы
, построить общее решение системы 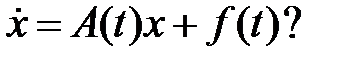
18. Можно ли найти все решения системы 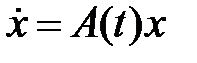 , линейной системы из
, линейной системы из 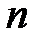 обыкновенных дифференциальных уравнений первого порядка, зная вектор-функции
обыкновенных дифференциальных уравнений первого порядка, зная вектор-функции 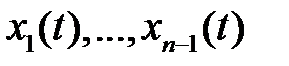 , являющиеся её линейно независимыми решениями?
, являющиеся её линейно независимыми решениями?
19. В чем состоит метод Лагранжа нахождения общего решения неоднородной линейной системы?
20. Как построить однородную линейную систему, имеющую заданную фундаментальную систему решений?
21. В чем состоит метод Эйлера интегрирования однородных линейных систем с постоянными коэффициентами? Как зависит структура фундаментальной системы решений от вида характеристического уравнения?
22. При каком условии линейная однородная система двух уравнений имеет частное решение, в котором искомые функции принимают заданные начальные значения при 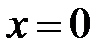 , и которое представимо в виде степенных рядов по степеням
, и которое представимо в виде степенных рядов по степеням 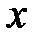 ?
?
23. Как найти общее решение однородной линейной системы двух уравнений при помощи степенных рядов?
24. При каких условиях однородная линейная система двух уравнений с постоянными коэффициентами приводится к одному однородному линейному уравнению второго порядка?
25. Сформулировать теорему существования и единственности для системы уравнений
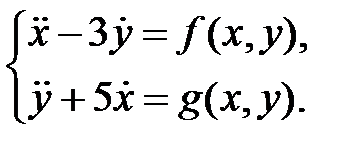
26. Пусть 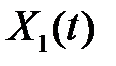 - фундаментальная матрица системы
- фундаментальная матрица системы 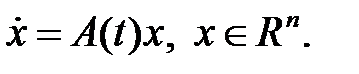 Доказать, что формула
Доказать, что формула 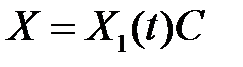 , где
, где  - произвольная постоянная размерности
- произвольная постоянная размерности 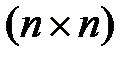 матрица,
матрица, 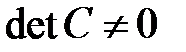 , содержит все фундаментальные матрицы этой системы.
, содержит все фундаментальные матрицы этой системы.
27. Докажите, что общее решение системы уравнений 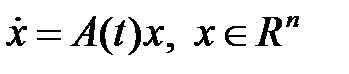 имеет вид
имеет вид 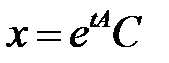 , если
, если 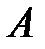 - квадратная постоянная матрица,
- квадратная постоянная матрица,  - произвольный постоянный вектор, а решение системы при начальном условии
- произвольный постоянный вектор, а решение системы при начальном условии 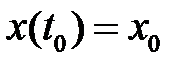 имеет вид
имеет вид 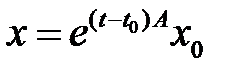 .
.
28. Укажите простой способ понижения числа уравнений в системе 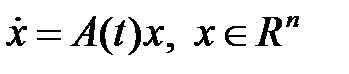 при известном ненулевом частном решении.
при известном ненулевом частном решении.
29. Докажите, что систему уравнений 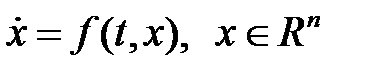 при помощи последовательных дифференцирований и исключения всех неизвестных функций, кроме одной, можно привести к одному дифференциальному уравнению
при помощи последовательных дифференцирований и исключения всех неизвестных функций, кроме одной, можно привести к одному дифференциальному уравнению 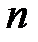 -го порядка. Предполагается, что вектор-функция обладает непрерывной производной нужного порядка.
-го порядка. Предполагается, что вектор-функция обладает непрерывной производной нужного порядка.
30. Известно, что первая компонента некоторого частного решения системы 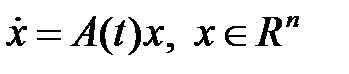 с постоянной матрицей коэффициентов имеет вид
с постоянной матрицей коэффициентов имеет вид 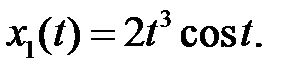 Каков наименьший возможный порядок матрицы
Каков наименьший возможный порядок матрицы 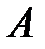 ?
?
31. Доказать, что линейная система
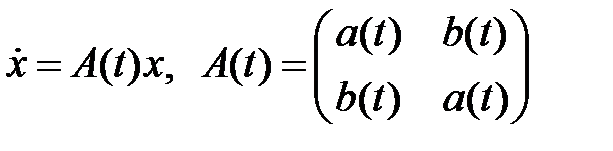
интегрируется в квадратурах.
32. Вычислить матрицу 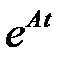 ,
, 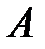 - данная матрица второго или третьего порядка.
- данная матрица второго или третьего порядка.
33. Какое пространство называется фазовым?
34. Пусть начало координат для системы уравнений
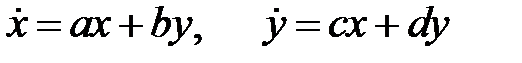
является фокусом. Выяснить, при каких соотношениях между коэффициентами спирали входят в особую точку, закручиваясь против часовой стрелки, при каких соотношениях - закручиваясь по часовой стрелке.
35. Пусть начало координат для системы уравнений предыдущей задачи является седлом или узлом. Выяснить, по каким направлениям интегральные кривые входят в начало (а в случае узла - и по какому направлению входит бесконечное количество кривых). Если начало координат является центром, выясните, как расположены главные оси эллипсов и какая из осей больше.
36. Нарисовать фазовую кривую системы
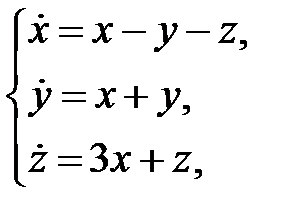
проходящую через точку 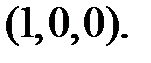
37. Чем отличается понятие устойчивости решения Ляпунову от понятия непрерывной зависимости решения от начальных данных?
38. Как судить об устойчивости (неустойчивости) нулевого решения однородной линейной системы с постоянными коэффициентами по характеристическим числам этой системы?
39. Как проводится исследование на устойчивость по первому приближению?
40. Доказать, что для того, чтобы нулевое решение системы линейных однородных дифференциальных уравнений с непрерывными коэффициентами было устойчивым, необходимо и достаточно, чтобы каждое решение этой системы было ограниченным.
41. Постройте пример системы
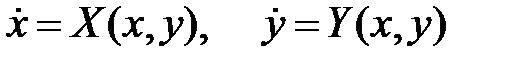
только с одним устойчивым решением, причем другие решения с любыми начальными данными существуют и ограничены при всех 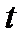 .
.
42. Привести пример решения системы дифференциальных уравнений, которое было бы устойчиво по Ляпунову, но не являлось бы асимптотически устойчивым. Может ли решение такой системы быть асимптотически устойчивым, но не являться устойчивым по Ляпунову?
43. Доказать, что если тривиальное решение линейной системы 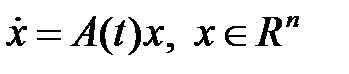 с непрерывной при
с непрерывной при 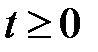 матрицей устойчиво по Ляпунову, то всякое решение этой системы ограничено на полуоси
матрицей устойчиво по Ляпунову, то всякое решение этой системы ограничено на полуоси 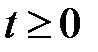 .
.
44. Доказать, что если каждое решение линейной однородной системы остается ограниченным при 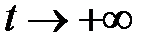 , то нулевое решение устойчиво по Ляпунову.
, то нулевое решение устойчиво по Ляпунову.
45. Доказать, что если каждое решение линейной однородной системы стремится к нулю при 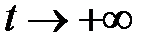 , то нулевое решение асимптотически устойчиво по Ляпунову.
, то нулевое решение асимптотически устойчиво по Ляпунову.
46. Доказать, что если линейная однородная система имеет хотя бы одно неограниченное при 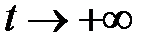 решение, то нулевое решение неустойчиво по Ляпунову.
решение, то нулевое решение неустойчиво по Ляпунову.
47. Пользуясь определением устойчивости по Ляпунову, выяснить, устойчивы ли решения данных уравнений с указанными начальными условиями:
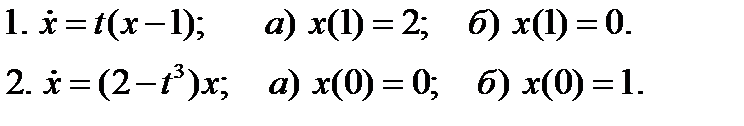
48. Может ли положение равновесия уравнения Ньютона быть устойчивым по Ляпунову, не будучи точкой локального минимума потенциальной энергии?
49. Может ли периодическое решение автономной системы, изображаемое на фазовой плоскости предельным циклом, быть асимптотически устойчивым?
50. Может ли периодическое решение автономной системы быть неустойчивым по Ляпунову, если на фазовой плоскости оно изображается предельным циклом, на который снаружи и изнутри наматываются спирально приближающиеся к циклу при движении в направлении возрастания времени фазовые кривые?
51. Может ли неустойчивое по Ляпунову положение равновесия стать после линеаризации устойчивым? Асимптотически устойчивым?
52. Может ли асимптотически устойчивое положение равновесия стать неустойчивым по Ляпунову после линеаризации?
53. Если одно из решений линейной системы обыкновенных дифференциальных уравнений первого порядка 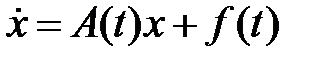 устойчиво (неустойчиво), то будут ли устойчивыми (неустойчивыми) все остальные?
устойчиво (неустойчиво), то будут ли устойчивыми (неустойчивыми) все остальные?
54. Если известно, что некоторое решение нелинейной системы обыкновенных дифференциальных уравнений устойчиво, то будет ли устойчивым нулевое решение (предполагается, что данная система имеет нулевое решение)?
55. Можно ли устойчивость ненулевого решения системы обыкновенных дифференциальных уравнений первого порядка исследовать с помощью теорем Ляпунова и Четаева?
56. Как можно определить устойчивость, асимптотическую устойчивость и неустойчивость некоторого решения для уравнения
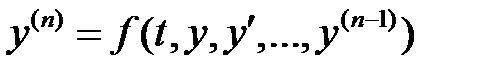 ?
?
57. Какие системы обыкновенных дифференциальных уравнений можно исследовать на устойчивость по первому приближению?
58. Можно ли теорему об устойчивости по первому приближению использовать при исследовании устойчивости «назад», т.е. при 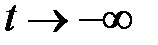 ?
?
59. Какие характерные точки покоя системы 2 линейных уравнений с постоянными коэффициентами известны?
60. В каком случае система линейных обыкновенных дифференциальных уравнений первого порядка будет автономной?
61. Можно ли исследовать устойчивость точки покоя автономной системы обыкновенных дифференциальных уравнений первого порядка, используя теорему об устойчивости по первому приближению?
62. Если нулевое решение системы двух линейных дифференциальных уравнений первого порядка с постоянными коэффициентами неустойчиво, то какие траектории может иметь эта система?
63. В каком случае систему обыкновенных дифференциальных уравнений второго порядка можно преобразовать к автономной?
64. Может ли автономная система двух обыкновенных дифференциальных уравнений первого порядка иметь в качестве своей траектории плоскую кривую, подобную знаку 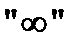 ?
?
65. Исследовать на устойчивость нулевое решение систем уравнений:
а) 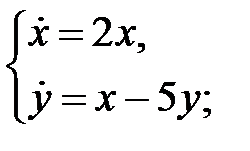 б)
б) 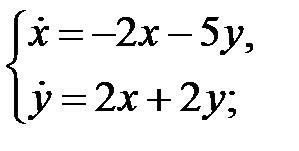 в)
в) 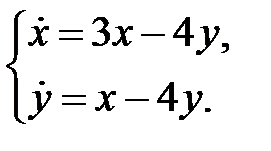
66. Исследовать на устойчивость нулевое решение систем уравнений :
а) 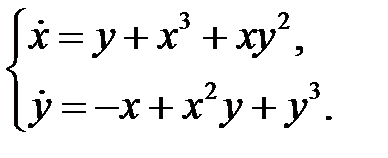 б)
б) 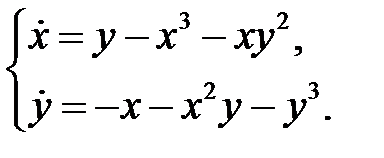
Применим ли к этим системам метод линеаризации?
67. Выяснить, устойчиво ли по Ляпунову решение системы
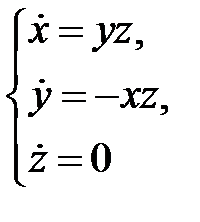
с начальным условием 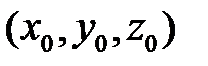 .
.
68. При каких значениях 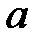 система уравнений
система уравнений
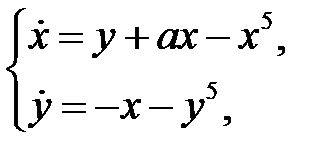
имеет устойчивую точку покоя 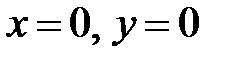 ?
?
69. При каких значениях 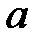 и
и 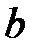 асимптотически устойчиво нулевое решение системы уравнений
асимптотически устойчиво нулевое решение системы уравнений
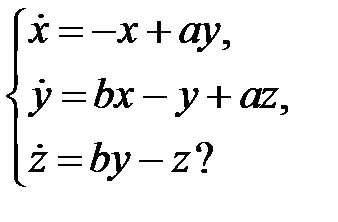
70. Является ли устойчивым в целом нулевое решение системы уравнений
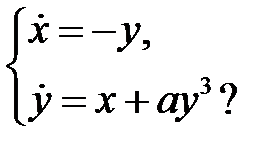
71. Исследовать поведение фазовых кривых систем уравнений:
а) 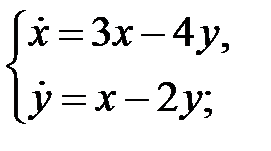 б)
б) 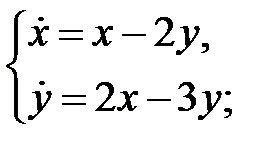 в)
в) 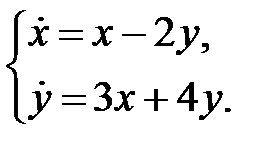
72. Выяснить типы положений равновесия систем уравнений:
а) 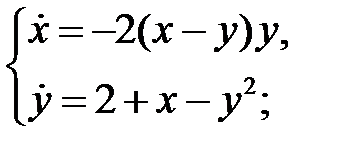 б)
б) 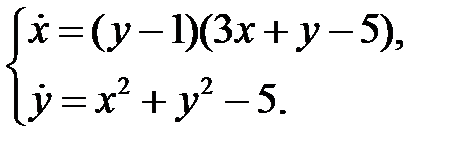
73. Доказать, что в системе
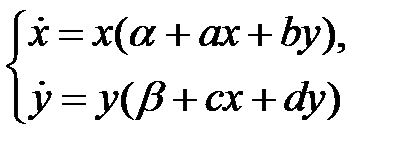
нет предельных циклов. Указание. При потере устойчивости фокусом система имеет первый интеграл, в виде произведения степеней трех линейных функций.
74. Доказать, что система уравнений
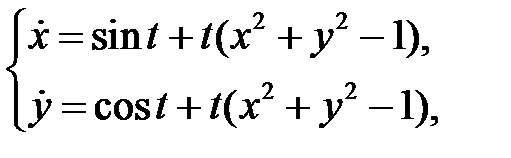
правые части которой не являются периодическими функциями относительно 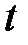 , имеет периодическое решение.
, имеет периодическое решение.
75. Доказать, что система
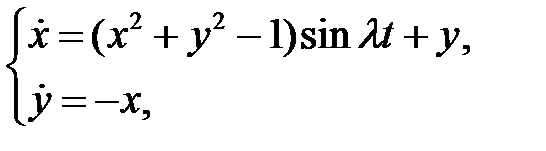
правые части которой суть периодические функции относительно 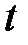 с периодом
с периодом 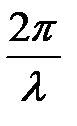 , имеет периодическое решение, период которого для
, имеет периодическое решение, период которого для 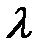 иррационально несоизмерим с периодом правых частей системы.
иррационально несоизмерим с периодом правых частей системы.
76. Доказать, что система
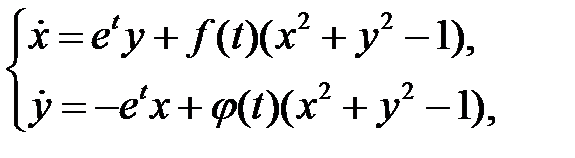
где 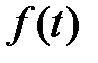 и
и 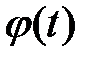 непрерывны при
непрерывны при 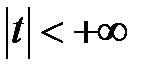 , имеет решение
, имеет решение 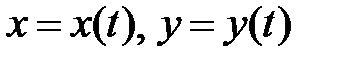 , которому соответствует замкнутая кривая на фазовой плоскости
, которому соответствует замкнутая кривая на фазовой плоскости 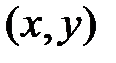 , но которое не является периодическим решением.
, но которое не является периодическим решением.
77. Какое условие достаточно наложить на собственные значения матрицы 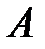 , чтобы система уравнений
, чтобы система уравнений 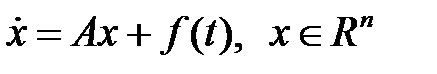 имела периодическое решение при всякой непрерывной вектор-функции
имела периодическое решение при всякой непрерывной вектор-функции 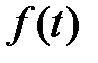 периода
периода 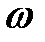 ?
?
78. Показать что система уравнений
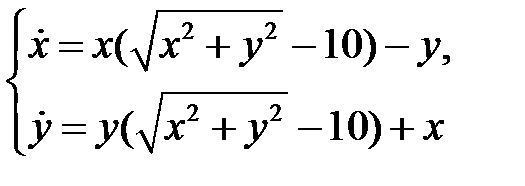
имеет один предельный цикл.
79. Пусть вещественные части собственных чисел матрицы 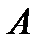 отрицательны;
отрицательны; 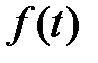 - непрерывная и ограниченная при всех
- непрерывная и ограниченная при всех 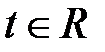 вектор-функция. Найти ограниченное при всех
вектор-функция. Найти ограниченное при всех 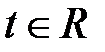 решение системы уравнений
решение системы уравнений 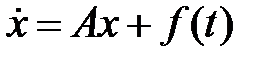 .
.
80. Составить линейную однородную систему дифференциальных уравнений, имеющую фундаментальную матрицу
. 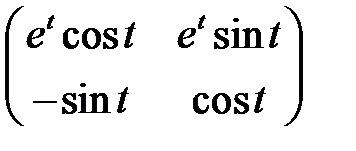 .
.
81. Проверить, являются данные функции
а) 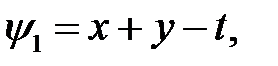 б)
б) 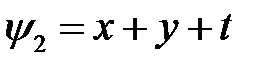
первыми интегралами системы
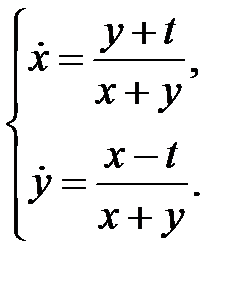
82. Найти все, не зависящие от времени и непрерывные на всей фазовой плоскости, первые интегралы системы
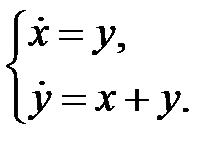
83. Числа 1 и 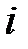 - собственные для матрицы
- собственные для матрицы 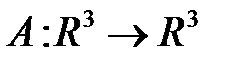 . Имеет ли уравнение
. Имеет ли уравнение 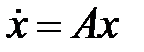 непрерывные в
непрерывные в 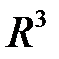 непостоянные первые интегралы?
непостоянные первые интегралы?
84. Числа 1 и -1 - собственные для матрицы 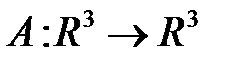 . Имеет ли уравнение
. Имеет ли уравнение 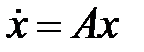 непрерывные в
непрерывные в 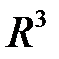 непостоянные первые интегралы?
непостоянные первые интегралы?
85. Для системы уравнений
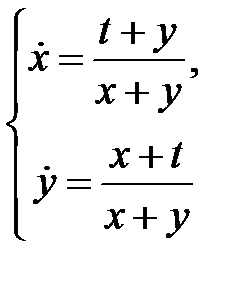
проверить, образуют ли данные пары функций
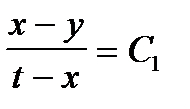 ,
, 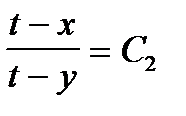
системы независимых интегралов.
86. Доказать, пользуясь теоремой Пикара, существование и единственность решения системы, удовлетворяющего поставленным начальным условиям:
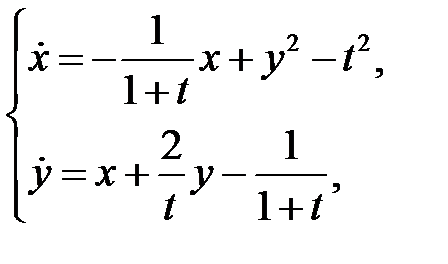
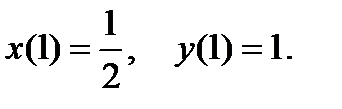
87. Найти голоморфное решение, удовлетворяющее поставленному начальному условию:
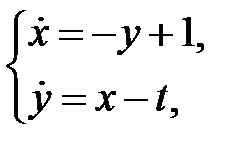
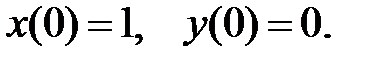
88. Какие начальные данные можно задавать, чтобы задача Коши заведомо имела единственное решение? Оценить область существования решения и область сходимости степенных рядов, представляющих решения данных систем:
а) 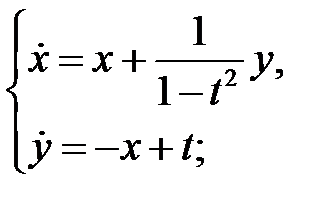 б)
б) 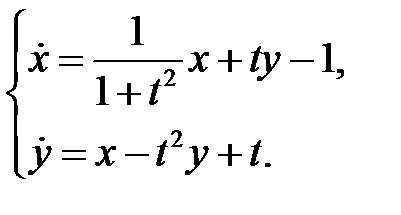
Решить систему уравнений.
89. 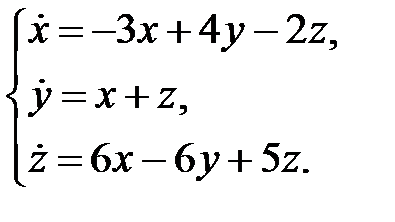 90.
90. 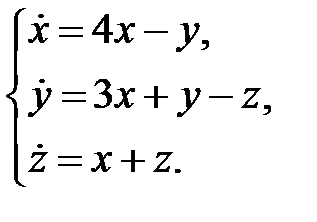
91. 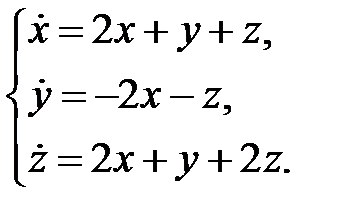 92.
92. 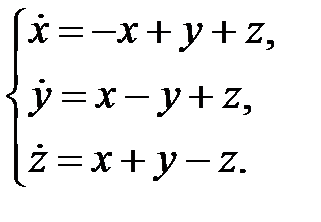
93. 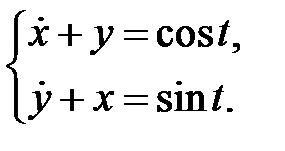 94.
94. 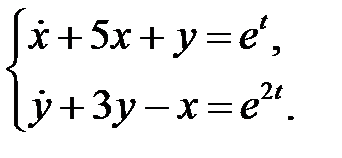
95. Записать в векторной форме систему уравнений
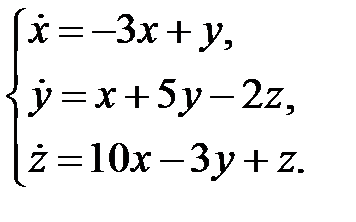
96. Записать покоординатно систему уравнений
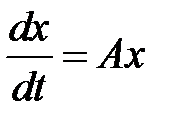 , где
, где 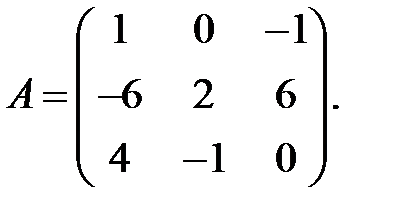
97. Пусть задано уравнение 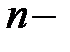 го порядка с постоянными коэффициентами
го порядка с постоянными коэффициентами 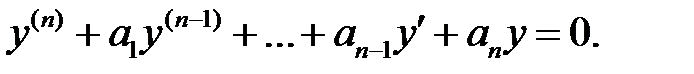
a) Свести его к системе уравнений 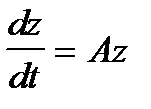 заменой
заменой 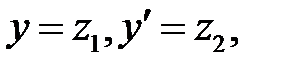
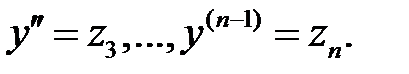 Какой вид имеет матрица
Какой вид имеет матрица 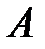 ?
?
б) Какой вид будет иметь система 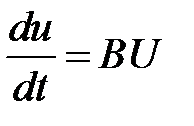 , получившаяся из уравнения пункта а) заменой
, получившаяся из уравнения пункта а) заменой
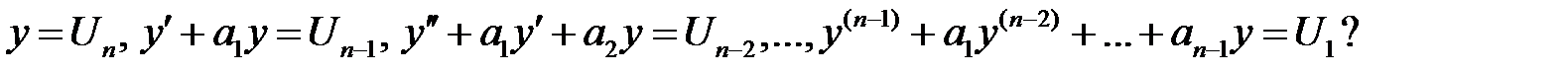
Как связаны между собой матрицы 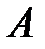 и
и 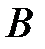 ?
?
98. Вычислить матрицу 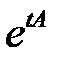 , пользуясь определением
, пользуясь определением
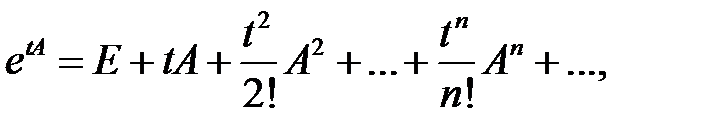
если матрица 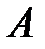 имеет вид:
имеет вид:
a) 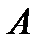 =
= 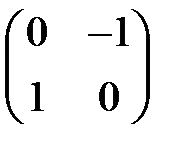 , б)
, б) 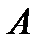 =
= 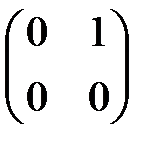 .
.
99. Показать, что если система уравнений 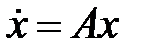 имеет своим решением вектор-функцию
имеет своим решением вектор-функцию 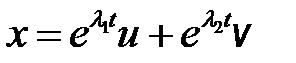 , где
, где 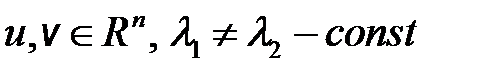 , то каждая из векторов-функций
, то каждая из векторов-функций 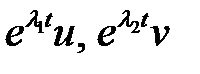 есть решение этой системы.
есть решение этой системы.
100. Если система уравнений 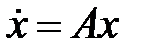 имеет своим решением вектор-функцию
имеет своим решением вектор-функцию 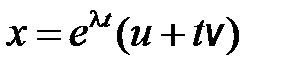 , где
, где 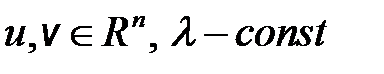 , то что можно сказать о кратности собственного значения
, то что можно сказать о кратности собственного значения 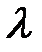 и каким алгебраическим уравнениям удовлетворяют векторы
и каким алгебраическим уравнениям удовлетворяют векторы 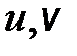 ?
?
101. Пусть собственные числа матрицы 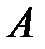 суть
суть 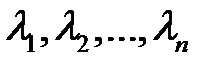 . Чему равны собственные числа
. Чему равны собственные числа 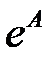 ?
?
102. Пусть собственные числа 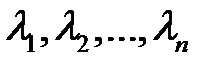 матрицы
матрицы 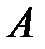 удовлетворяют условию
удовлетворяют условию 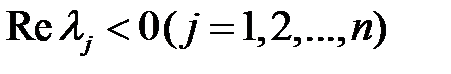 . Доказать, что
. Доказать, что 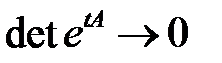 при
при 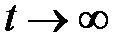 .
.
ГЛАВА 7








