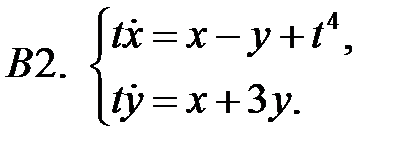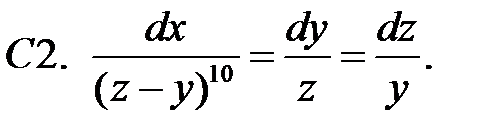Задание № 25. Линейные неоднородные системы.
Метод неопределенных коэффициентов
Найти общие решения систем 
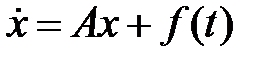методом неопределенных коэффициентов.
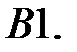Определить вид частного решения системы 
.
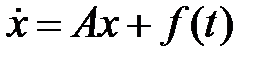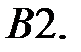Применяя метод исключения, решить систему.
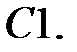Найти частное решение неоднородной системы.
Модель «затраты-выпуск».
Рассмотрим ситуацию, в которой повышение спроса на каждый продукт индуцирует приращение выпуска. Превышение спроса на первый продукт в период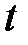 
может быть представлена разностью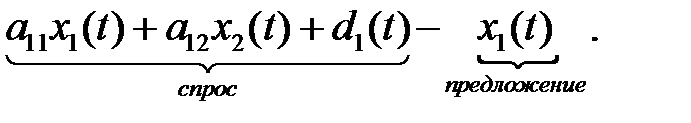 
Приращение выпуска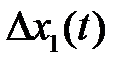 
подбирается в точности равным превышению спроса
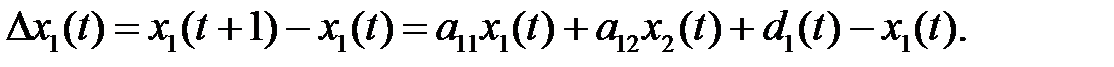
Процесс регулирования выпуска для двухсекторной экономики может быть представлен системой двух дифференциальных уравнений:
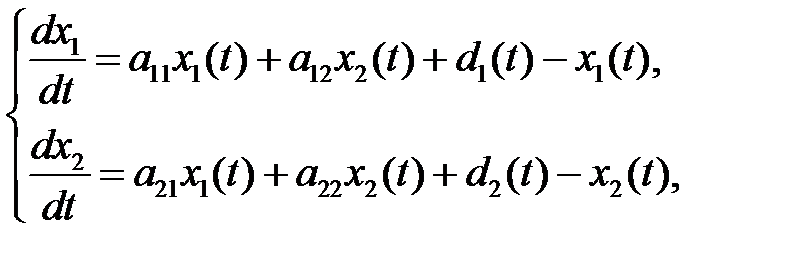
где коэффициенты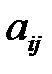 
означают затраты 
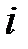-го продукта на производство единицы 
-го продукта в стоимостном выражении. Эта система может быть записана в матричном виде:
.
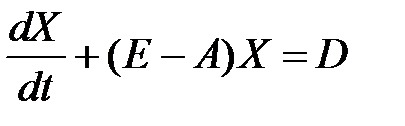Решить эту систему, если
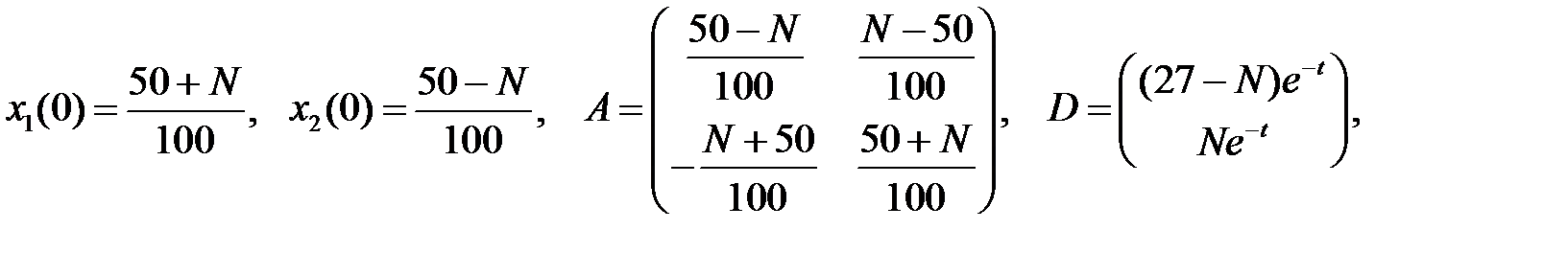
где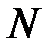 
- номер варианта.
1. 
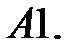
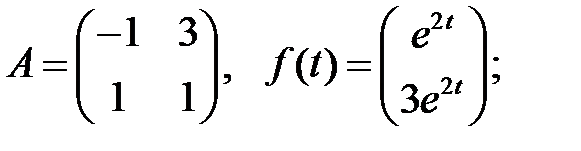
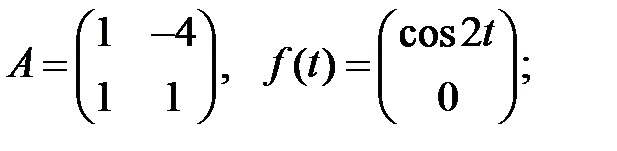
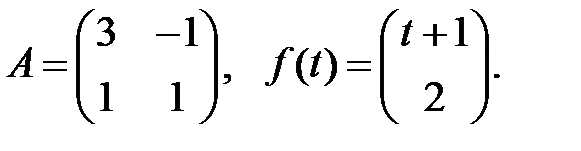
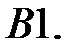
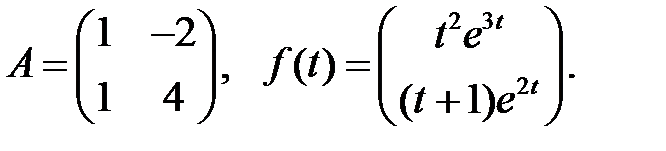
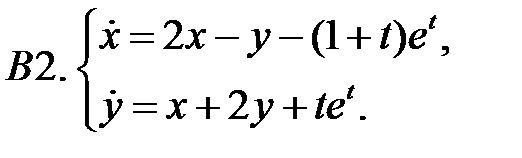
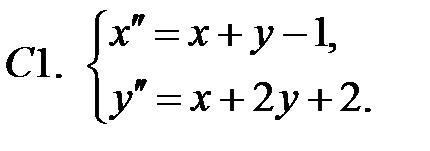
2. 
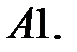
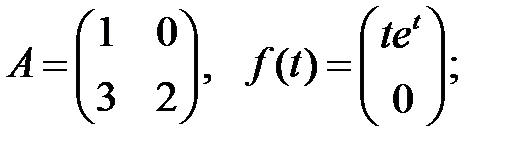
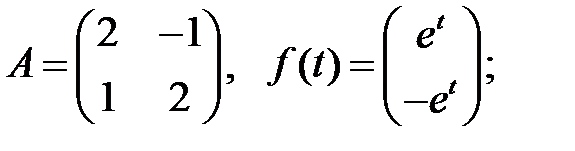
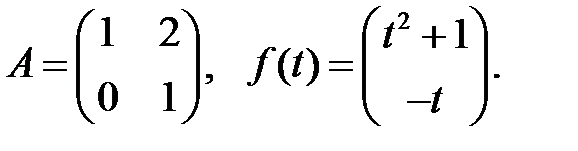
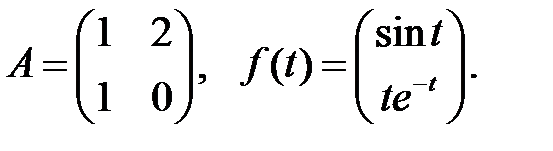
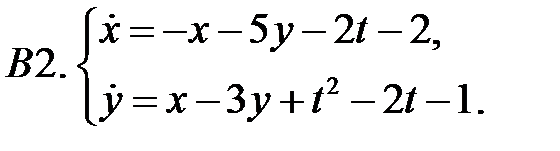
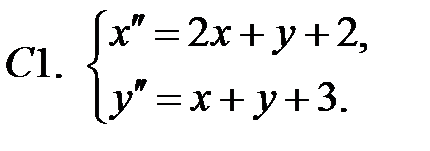
3. 
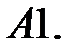
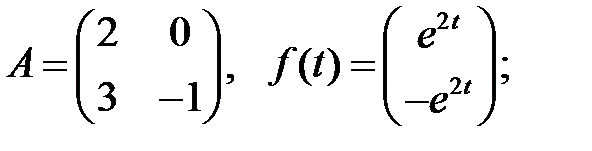
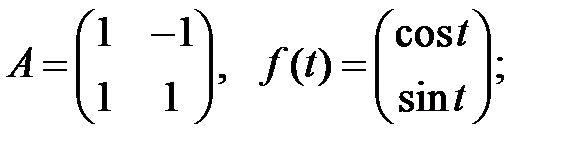
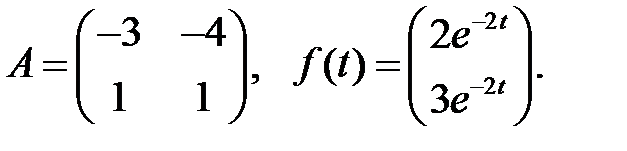
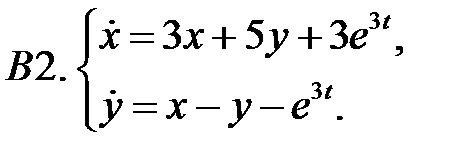
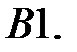
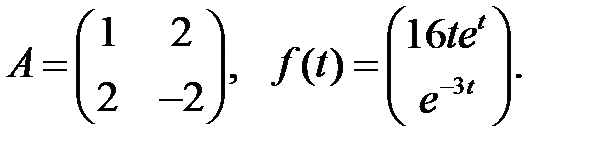
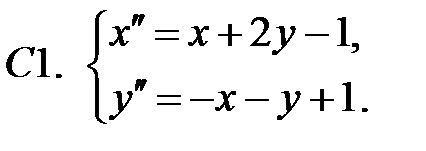
4. 
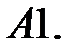
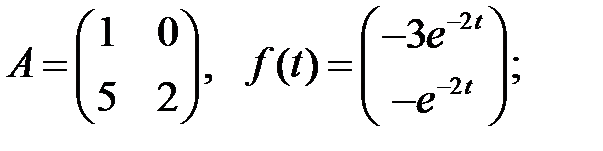
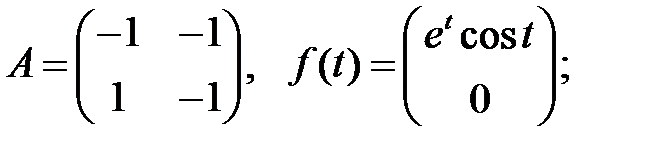
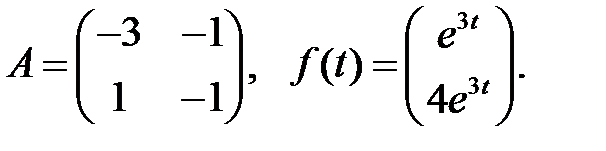
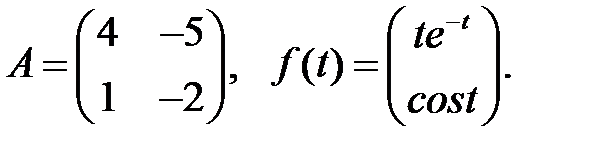
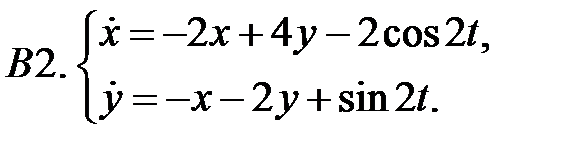
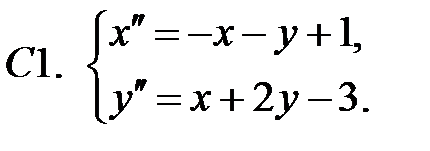
5. 
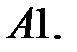
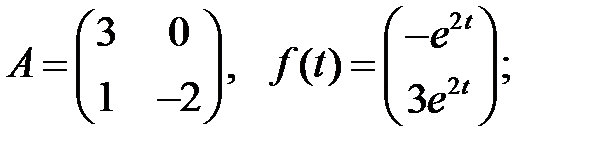
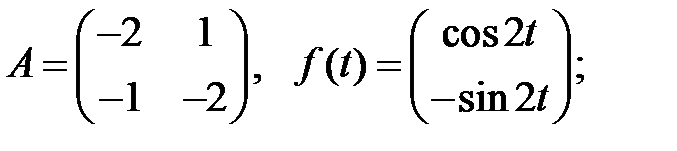
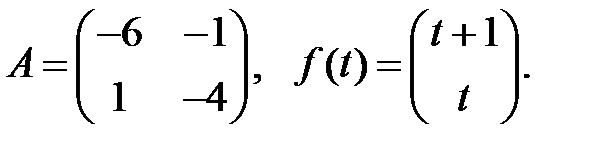
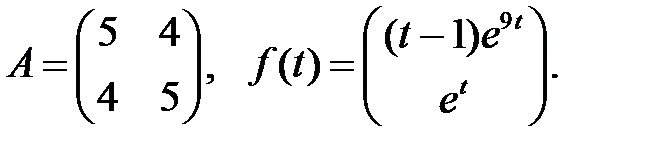
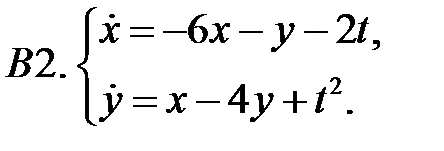
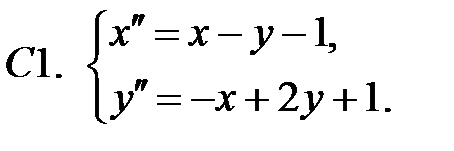
6. 
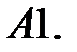
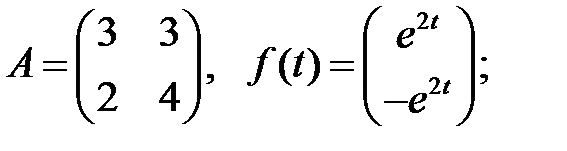
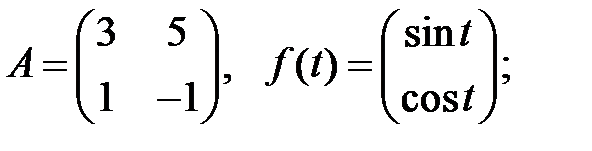
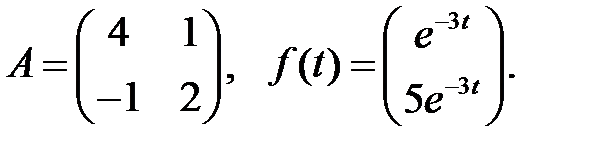
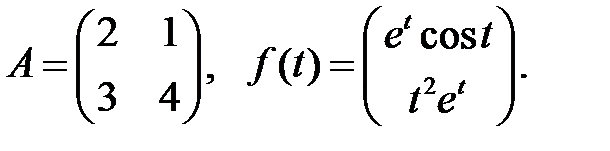
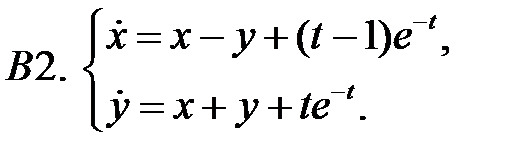
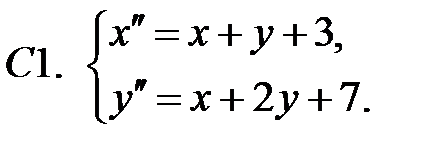
7. 
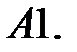
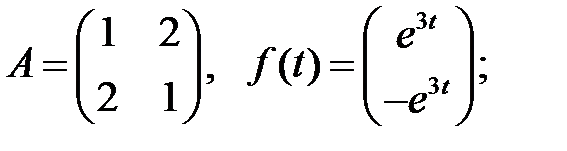
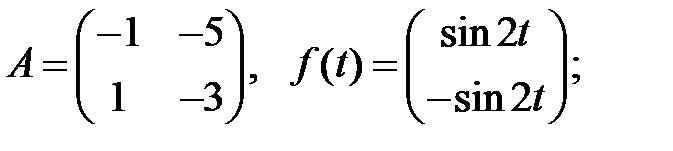
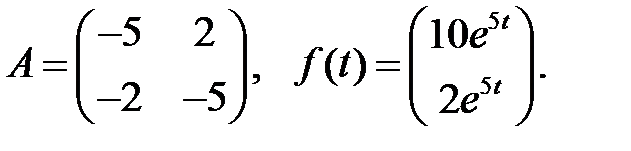
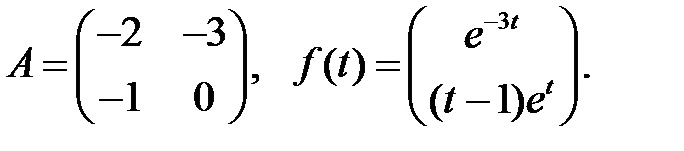
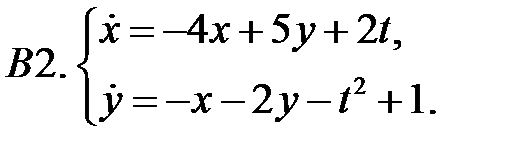
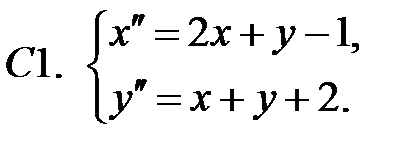
8. 
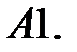
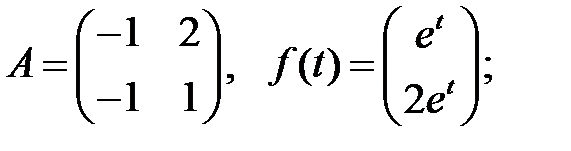
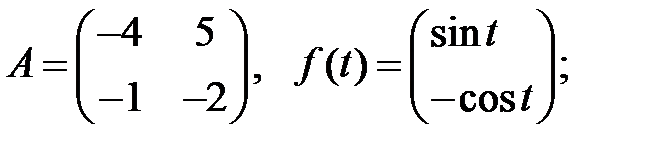
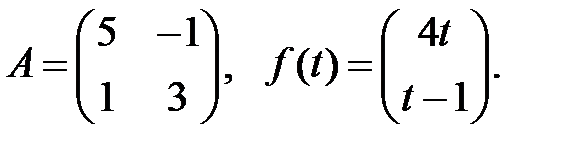
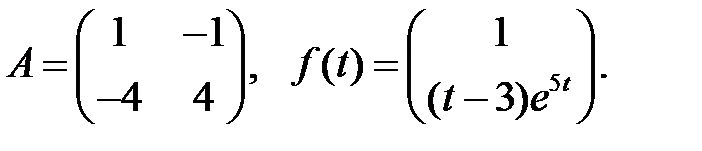
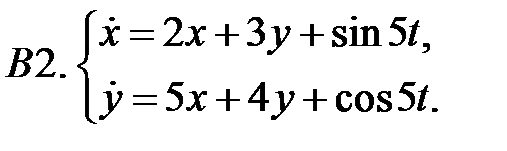
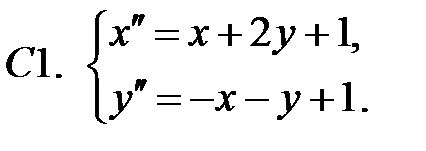
9. 
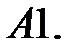
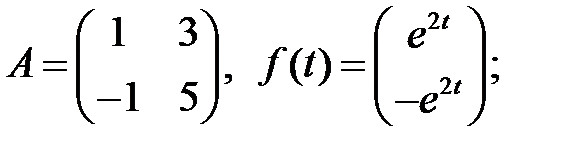
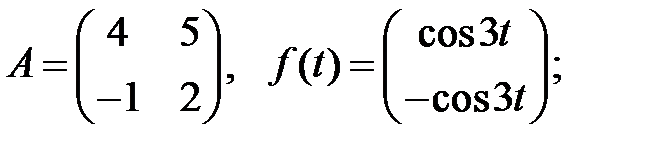
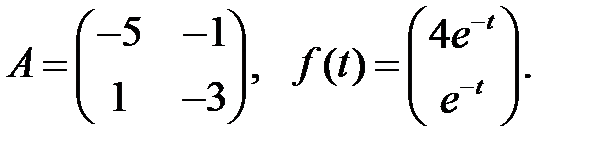
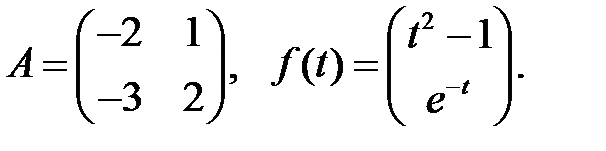
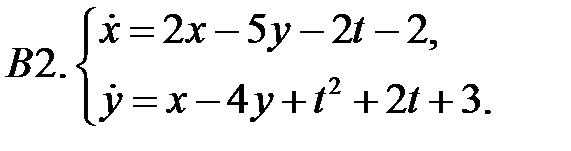
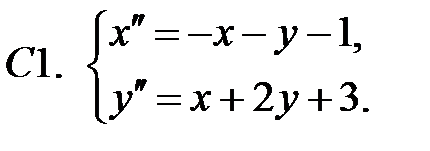
10. 
. 
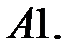
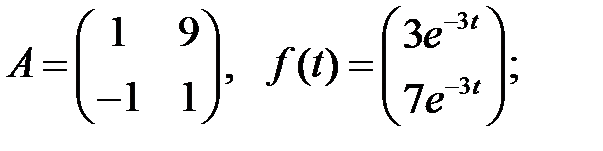
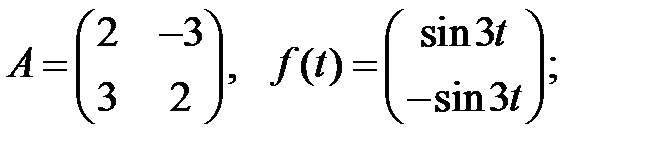
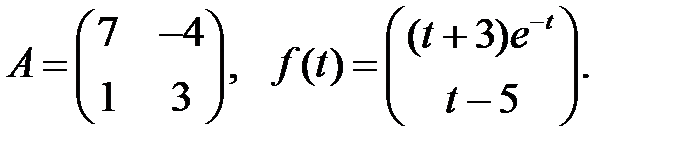
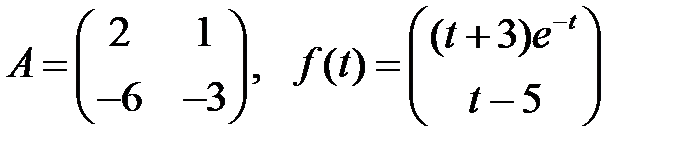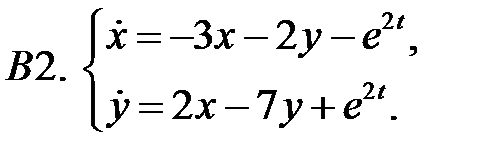
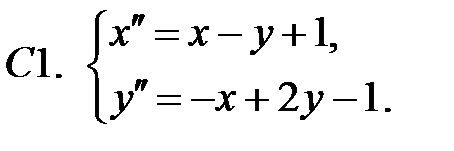
11. 
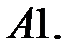
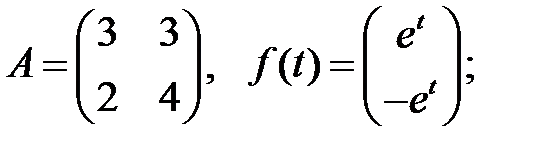
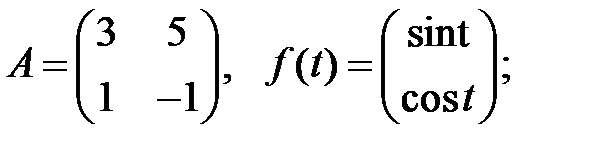
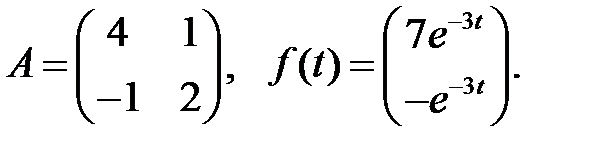
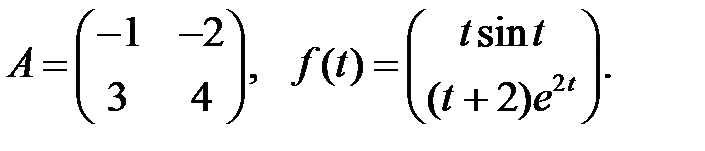
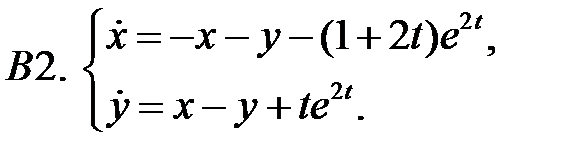
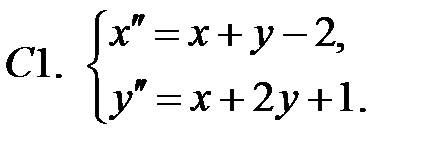
12. 
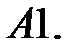
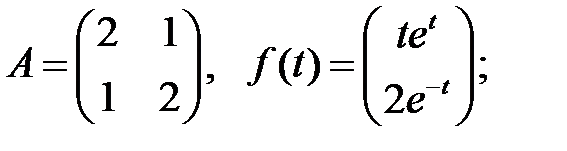
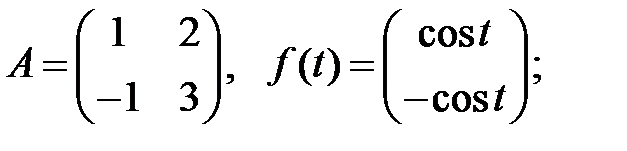
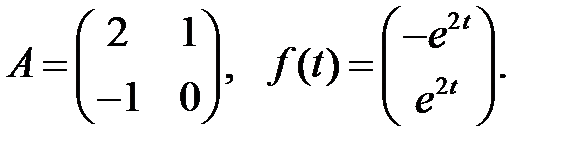
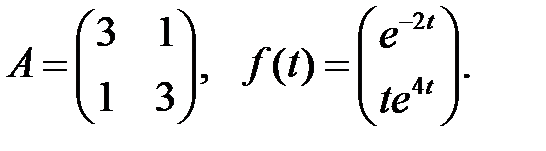
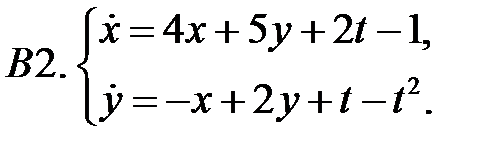
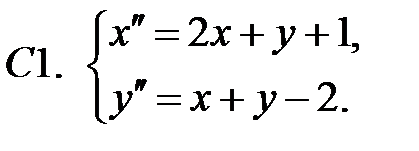
13. 
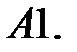
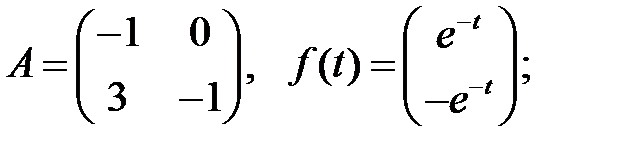
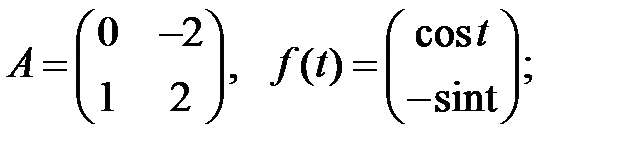
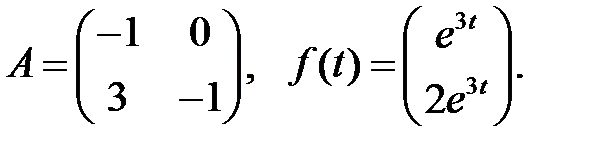
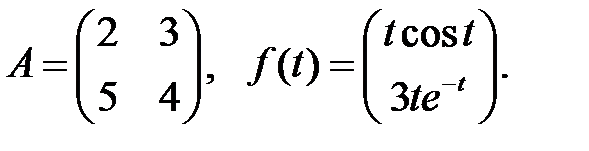
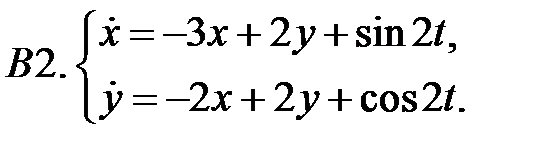
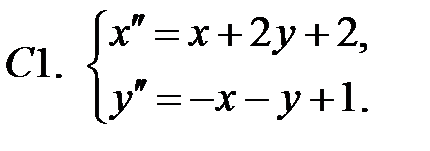
14. 
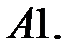
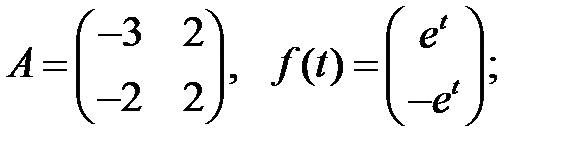
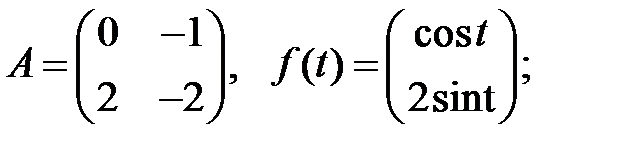
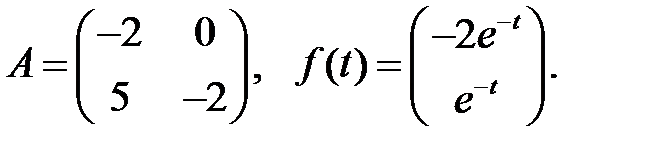
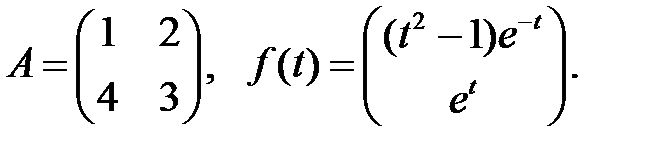
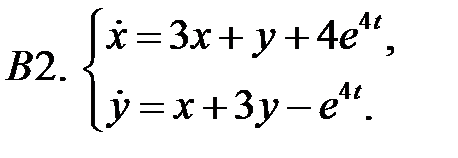
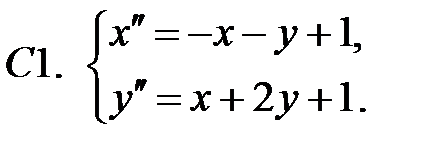
15. 
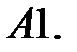
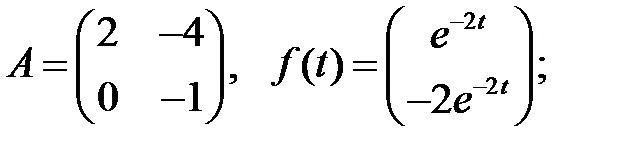
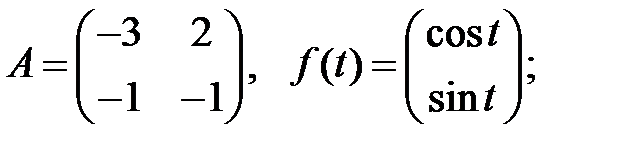
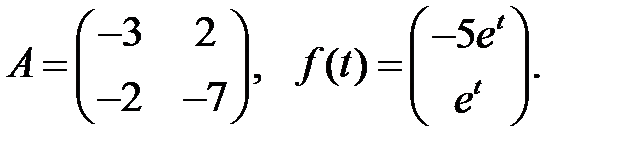
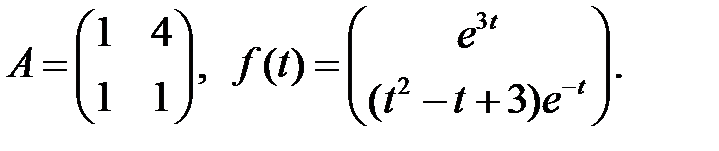
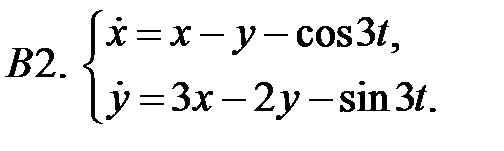
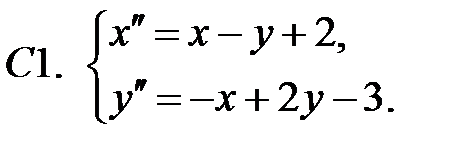
16. 
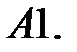
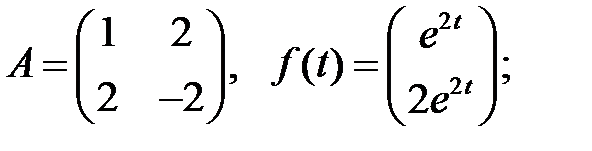
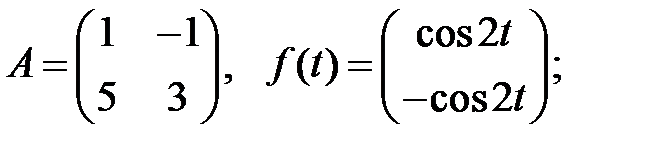
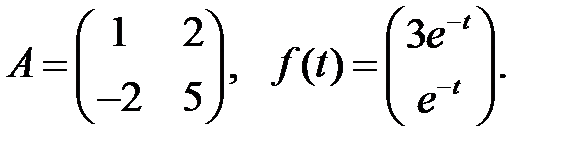
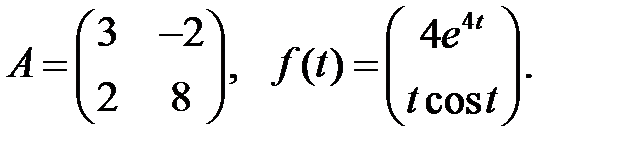
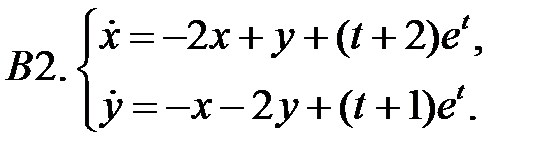
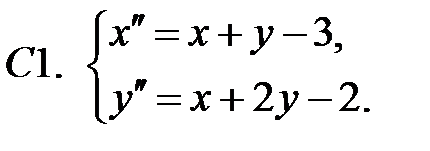
17. 
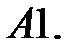
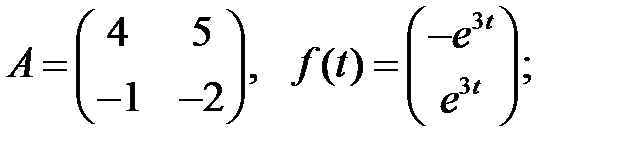
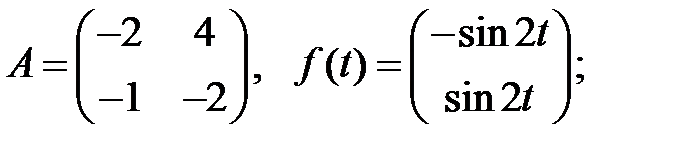
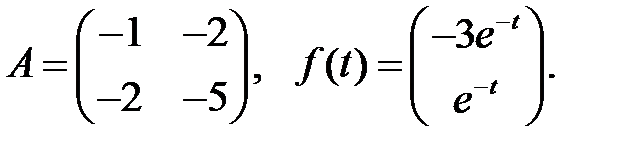
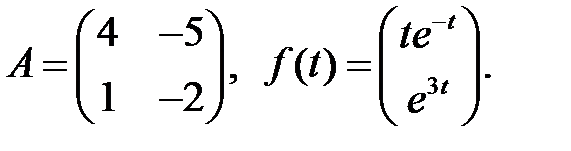
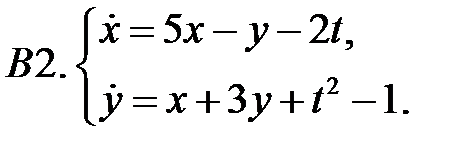
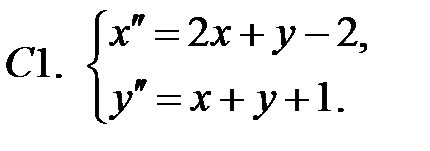
18. 
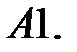
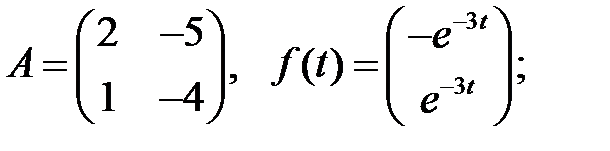
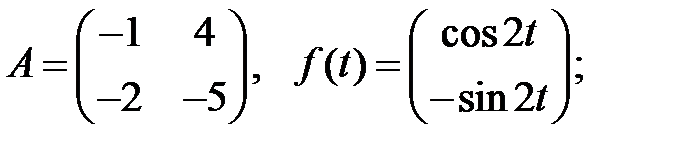
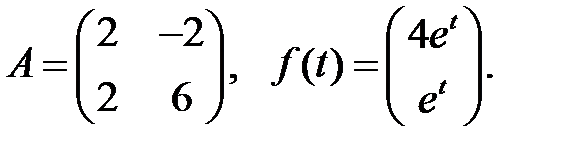
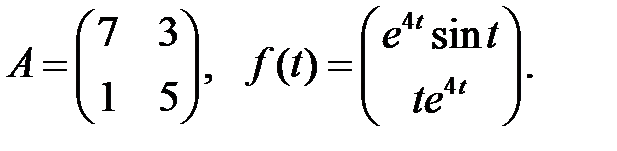
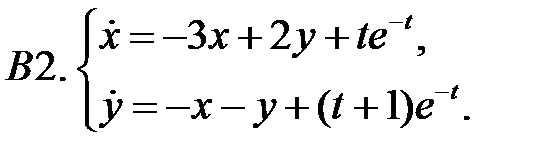
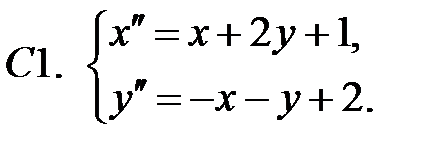
19. 
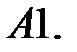
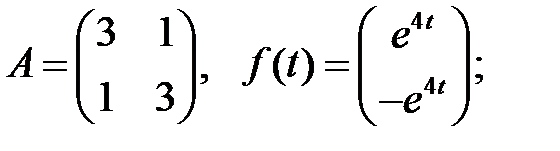
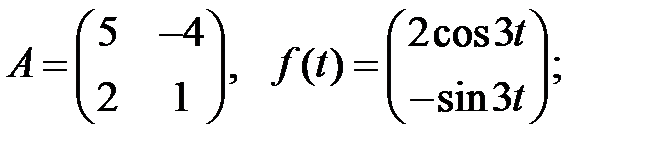
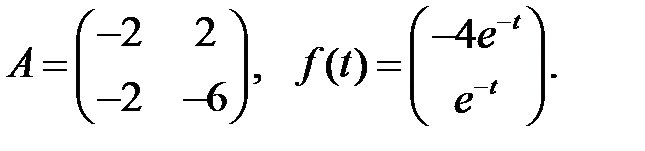
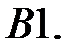
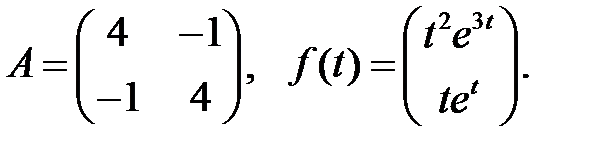
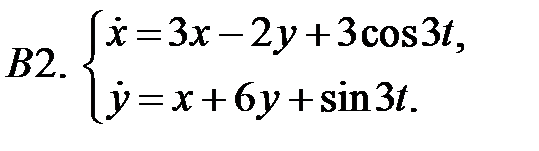
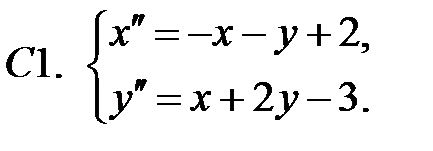
20. 
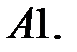
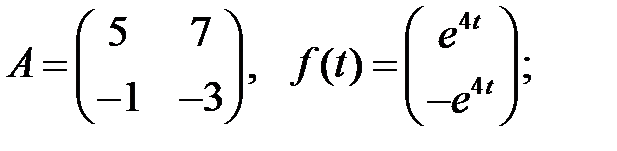
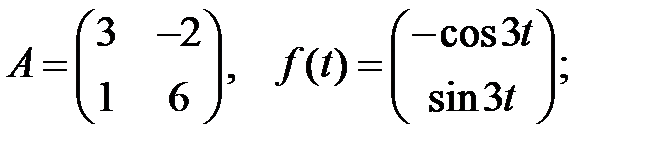
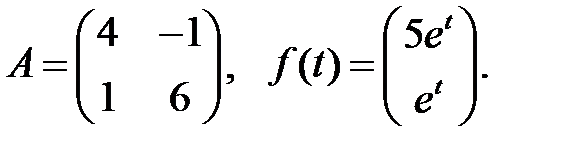
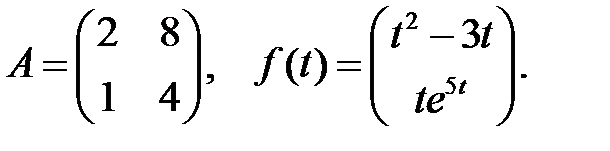
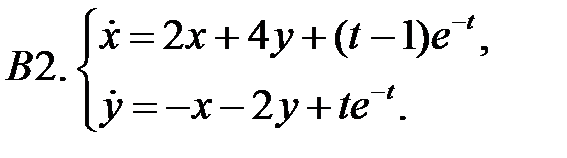
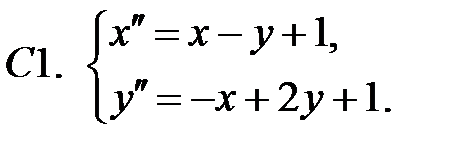
21. 
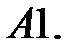
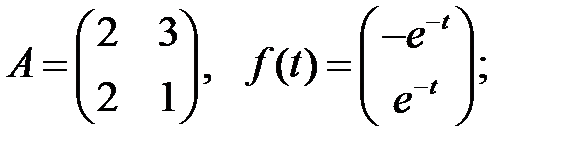
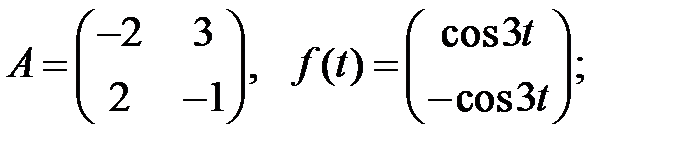
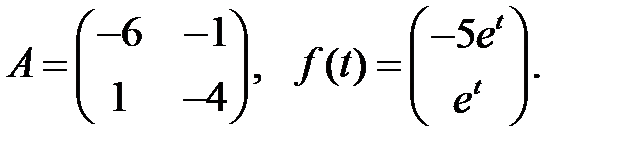
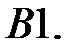
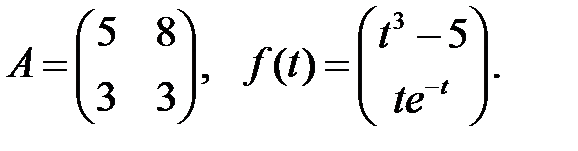
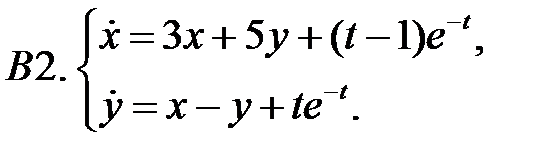
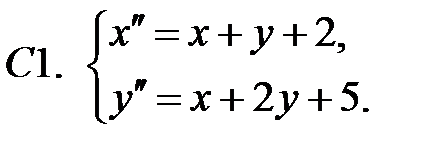
22. 
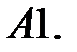
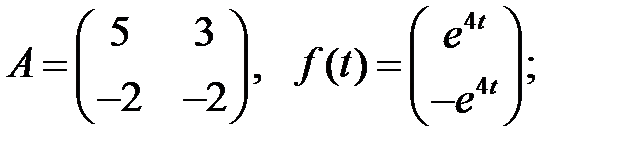
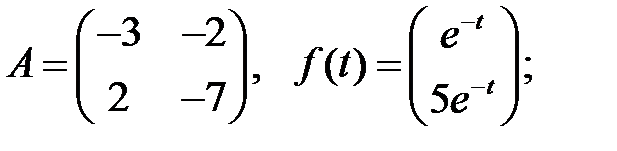
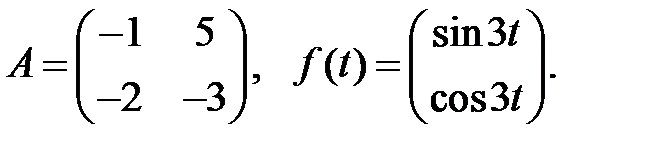
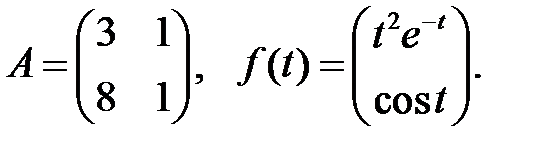
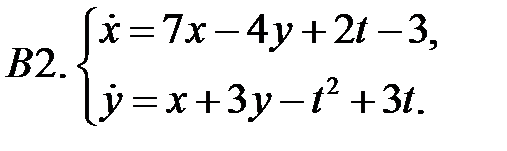
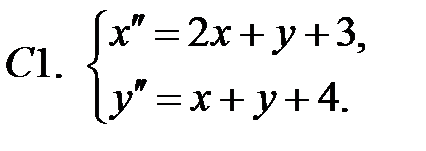
23. 
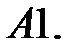
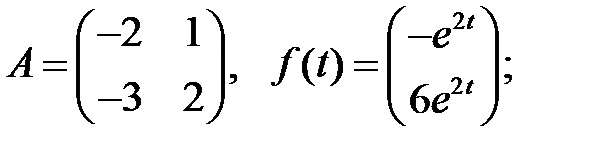
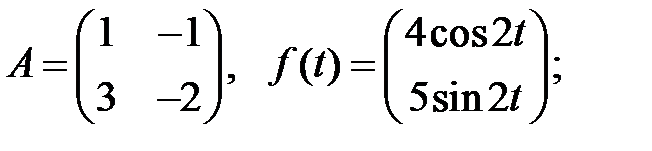
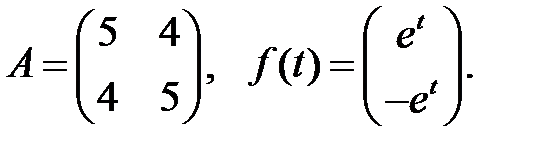
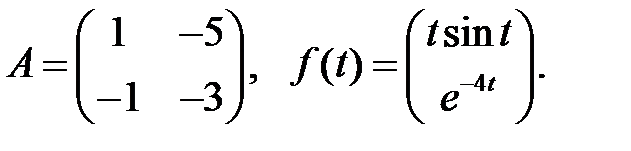
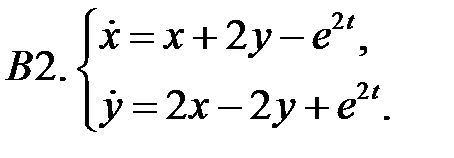
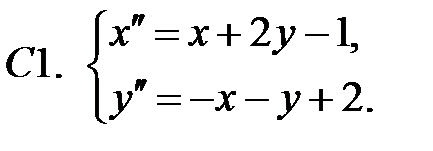
24. 
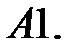
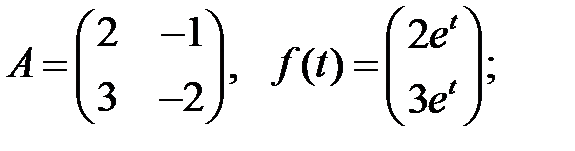
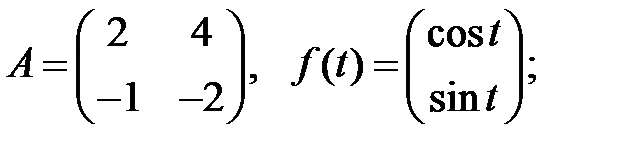
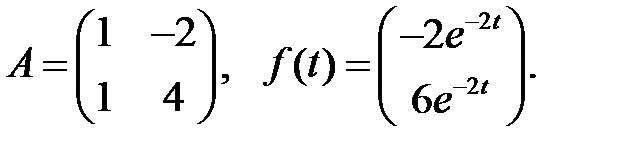
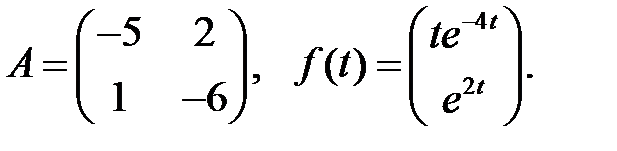
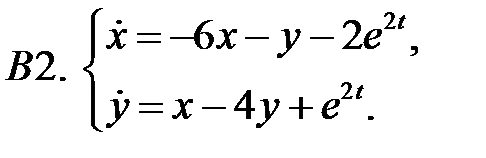
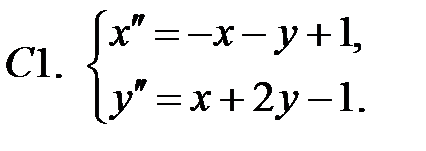
25. 
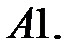
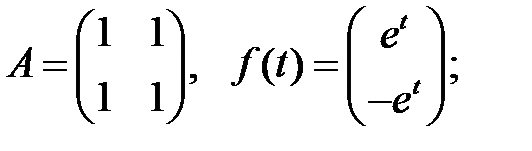
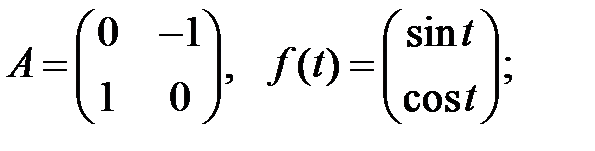
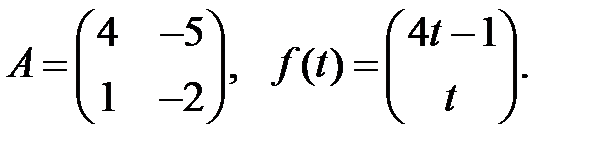
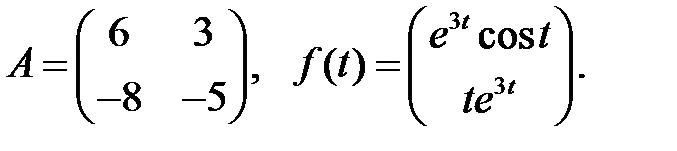
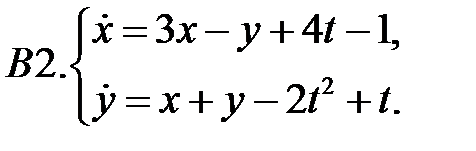
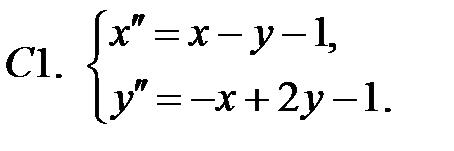
Задание № 26. Линейные неоднородные системы. Метод Лагранжа
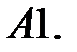Найти общие решения систем 
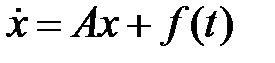методом Лагранжа.
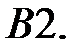Производя замену аргумента 
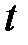по формуле 
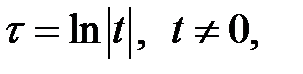решить систему.
Математическая теория эпидемий.
Предположим, что некоторая популяция, состоящая из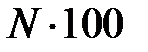 
особей, подразделяется на три группы. В первую из них включаются особи, которые восприимчивы к некоторой болезни, но здоровы. Число таких особей в момент времени 
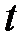обозначим через 
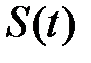. Во вторую группу объединяются особи, которые являются инфекционными – они сами больны и являются источником распространения болезни. Число таких особей в популяции в момент времени 
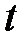обозначим через 
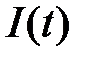. Третью группу составляют особи, которые здоровы и обладают иммунитетом к данной болезни. Число таких особей в момент 
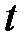обозначим через 
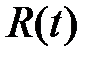. Таким образом,
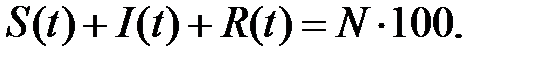(1)
Предположим, что в случае, когда число инфекционных особей превосходит некоторое фиксированной число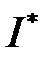 
, скорость изменения числа восприимчивых к болезни особей будет пропорциональна числу самих восприимчивых особей, т.е.
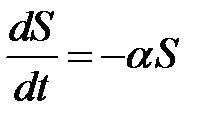. (2)
Что же касается скорости изменения числа инфекционных, но выздоравливающих особей, то ее будем считать пропорциональной числу инфекционных особей.
Будем считать также, что когда число инфекционных особей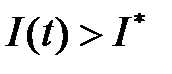 
, то они способны заражать восприимчивых к болезни особей. Последнее означает, что принимается во внимание факт изоляции инфекционных особей. Поэтому скорость изменения числа инфекционных особей представляет разность за единицу времени между вновь заболевшими особями и теми, которые уже выздоравливают. Итак,
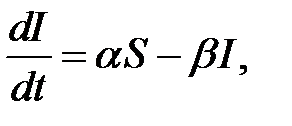(3)
где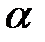 
- коэффициент заболеваемости, 
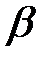- коэффициент выздоровления. Наконец, скорость изменения числа выздоравливающих особей задается уравнением
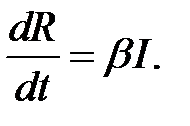(4)
Решить систему уравнений (2), (3), (4) в предположении, что в момент времени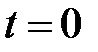 
в популяции нет особей с иммунитетом, т.е. 
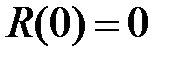и что первоначально число инфекционных особей равно 
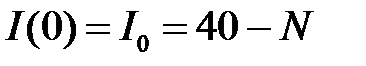и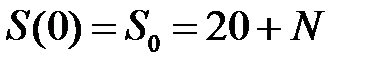 
. Изобразить графики изменения числа особей с ростом 
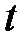в каждой из трех групп.
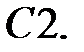Построить независимые интегралы системы.
1. 
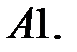
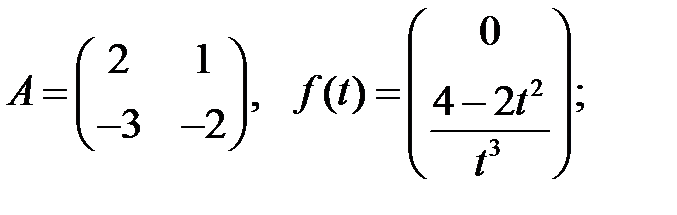
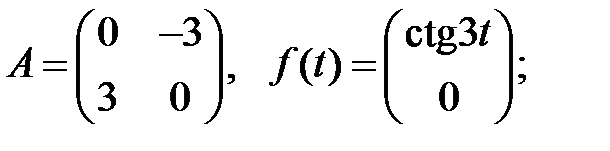
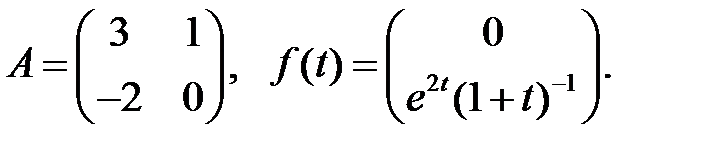
Вычислить якобиан 
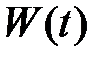, составленный из решений
, 
, 
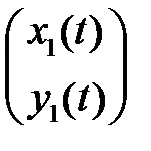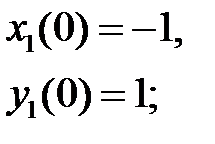
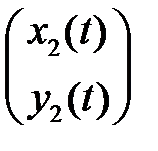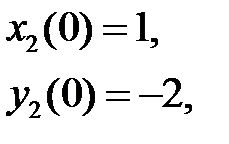
системы
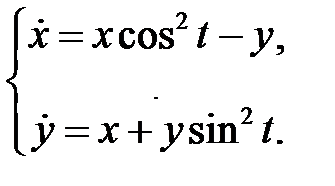
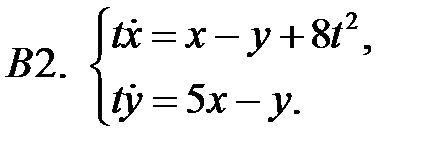
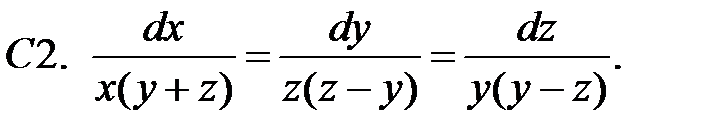
2. 
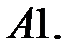
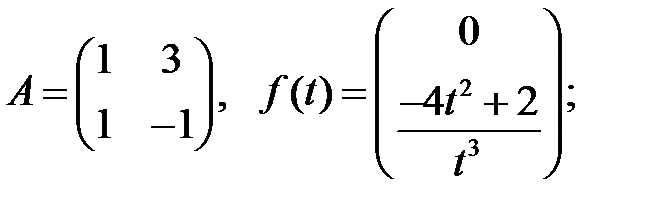
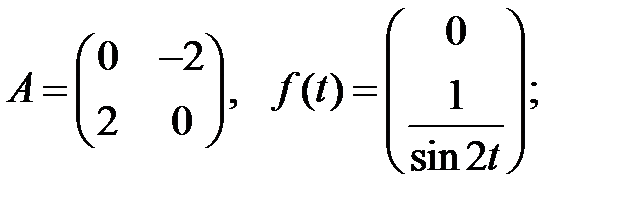
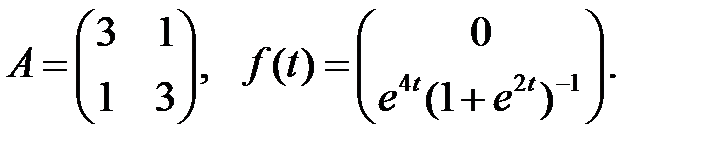
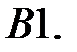Найти решение системы
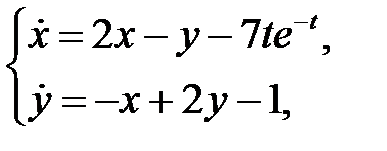
которое остается ограниченным при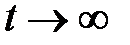 
.
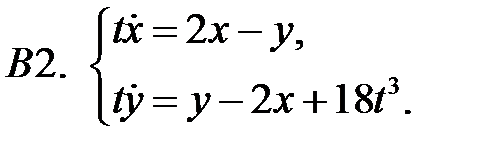
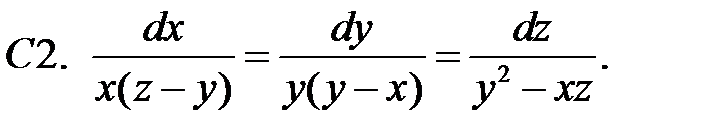
3. 
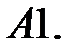
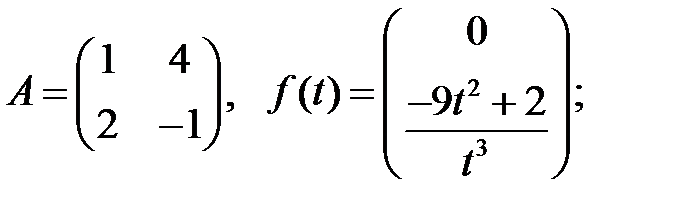
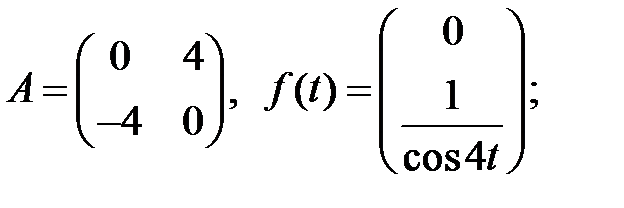
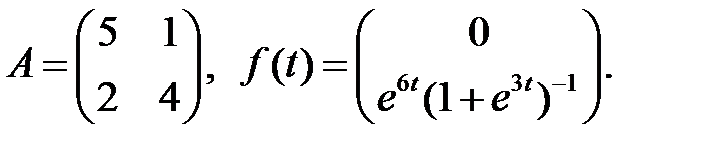
При каких значениях 
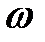система
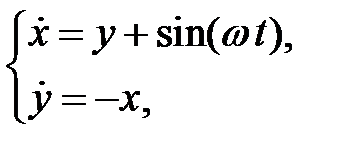
имеет периодические решения?
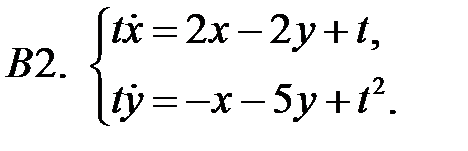
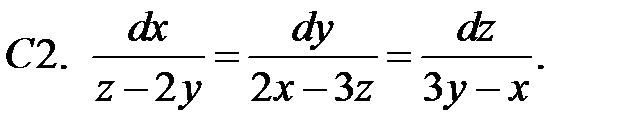
4. 
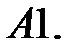
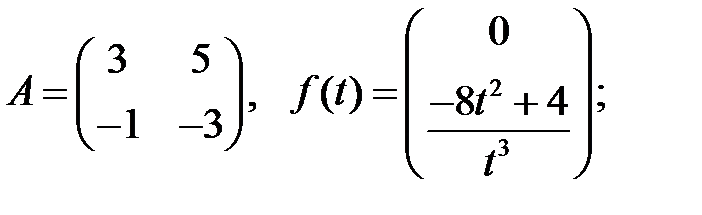
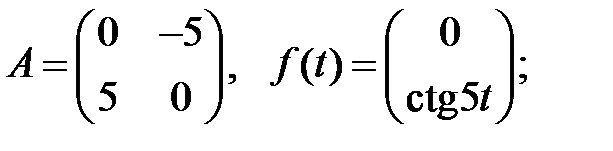
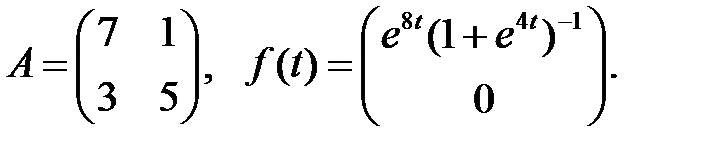
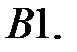Найти решение системы
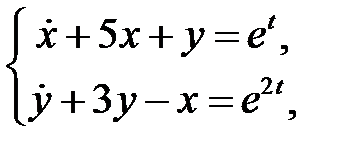
которое остается ограниченным при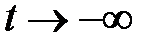 
.
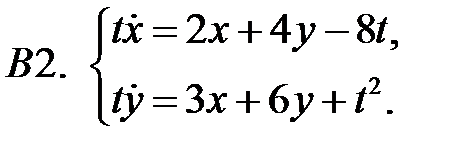
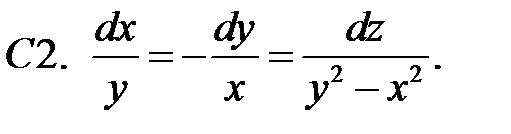
5. 
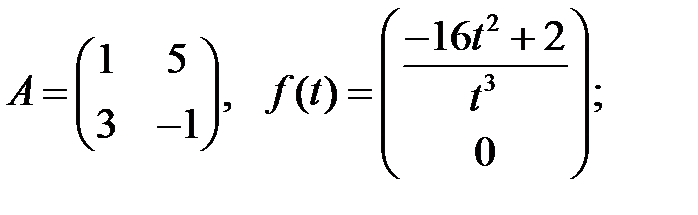
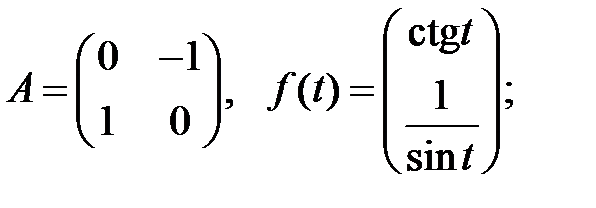
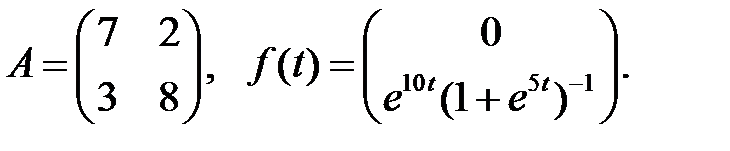
Найти периодическое решение системы
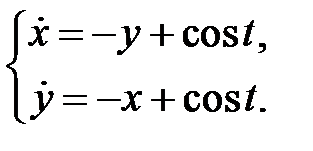
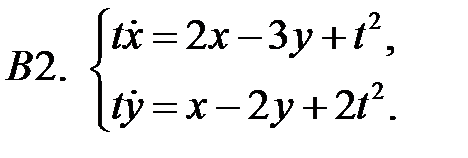
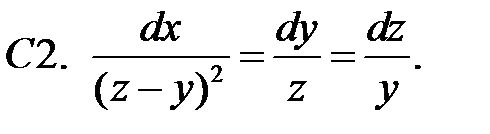
6. 
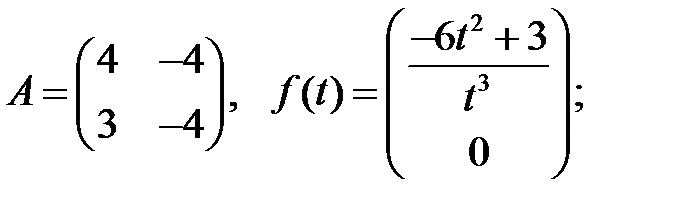
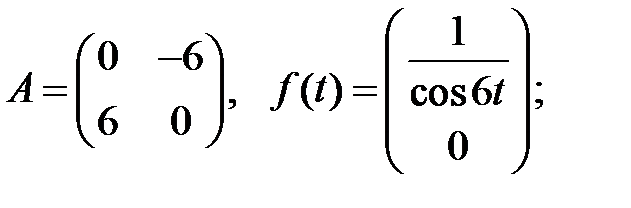
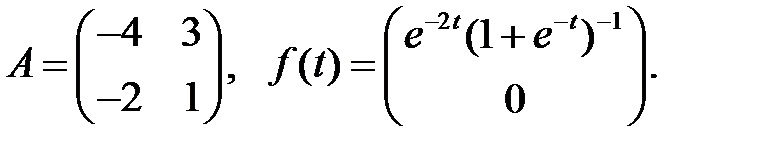
Найти решения системы
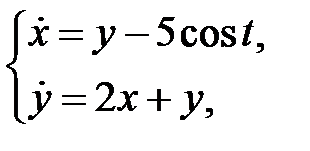
которые остаются ограниченными при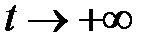 
.
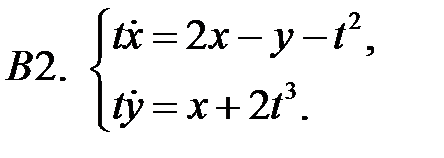
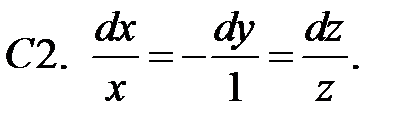
7. 
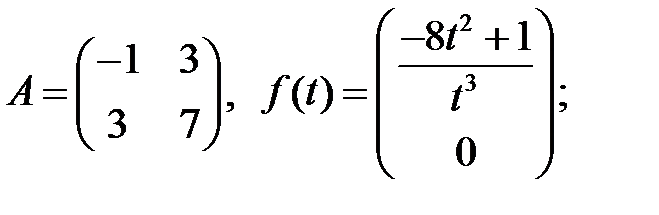
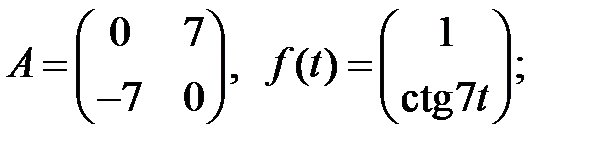
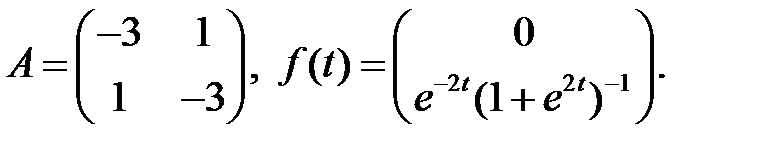
Найти решение системы
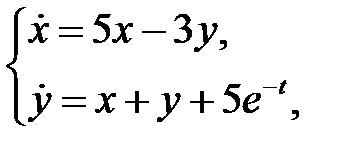
которое остается ограниченным при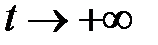 
.
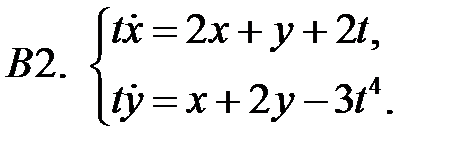
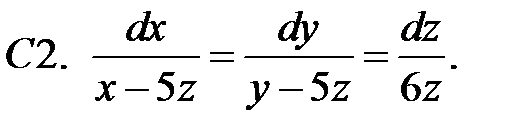
8. 
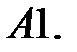
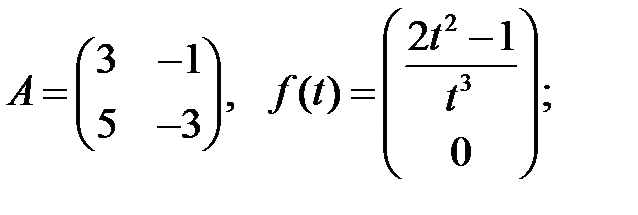
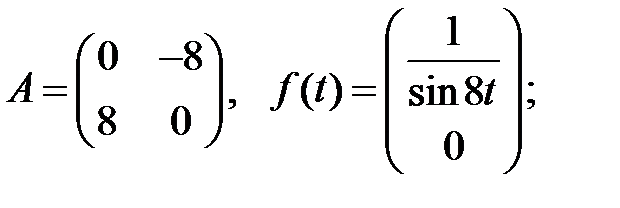
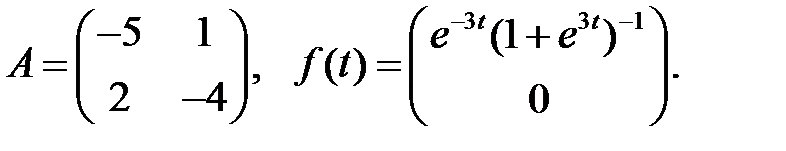
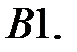Найти периодическое решение системы
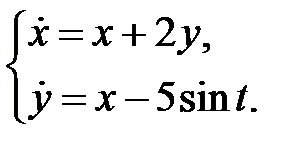
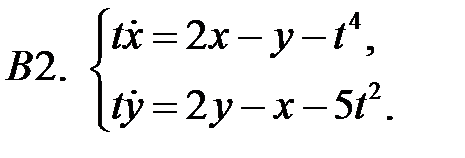
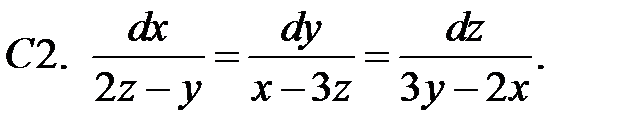
9. 
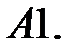
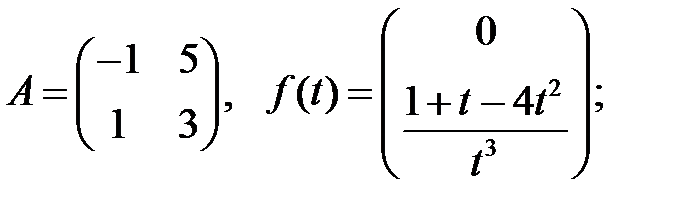
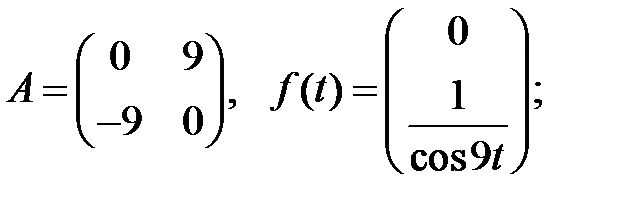
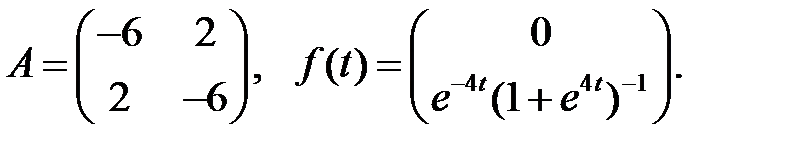
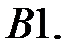Найти решения системы
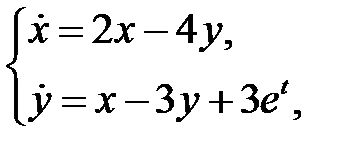
которые остаются ограниченными при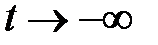 
.
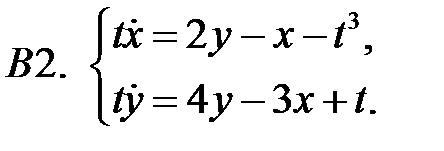
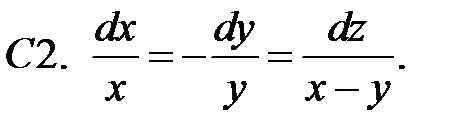
10. 
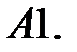
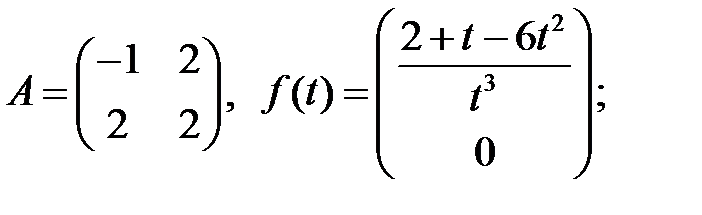
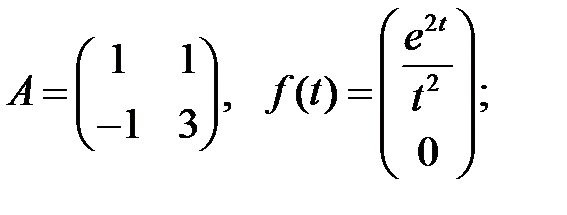
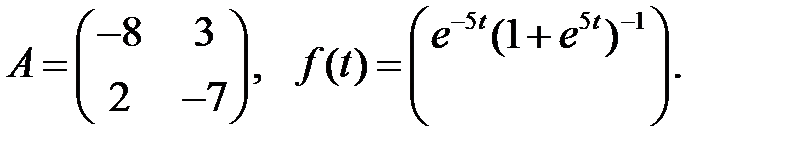
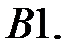Найти периодическое решение системы
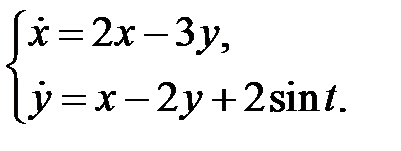
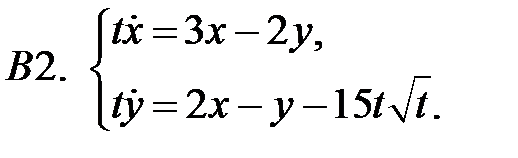
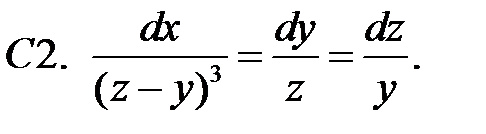
11. 
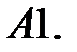
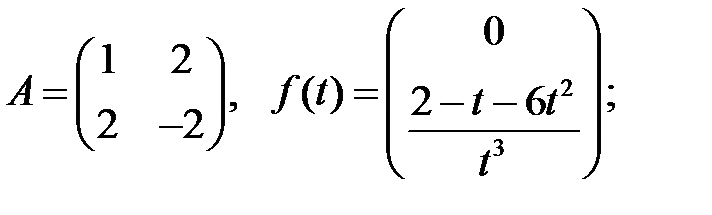
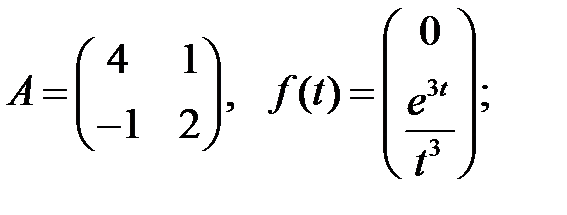
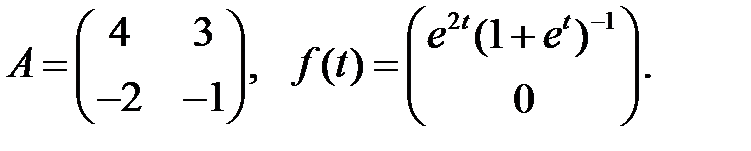
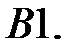Найти ограниченное при 
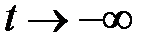решение системы
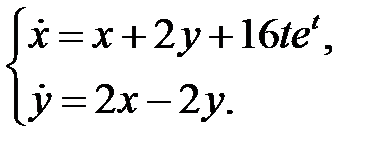
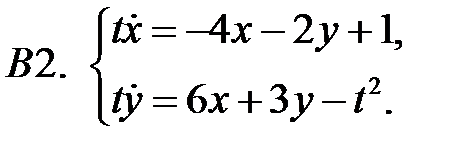
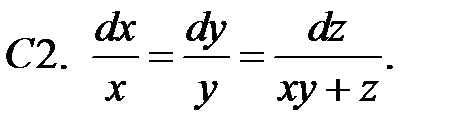
12. 
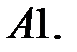
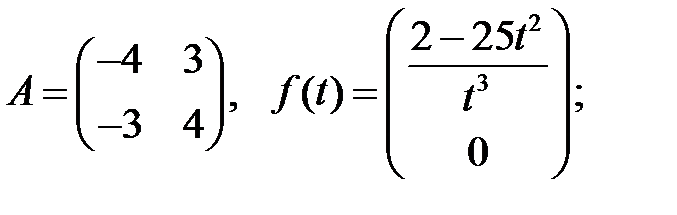
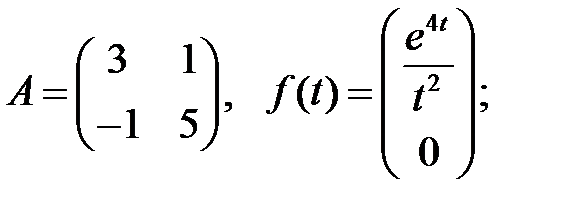
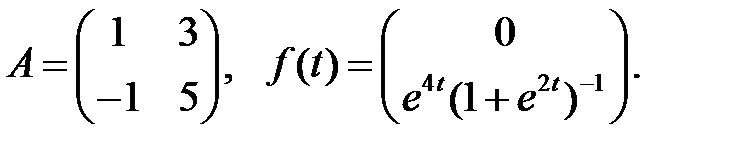
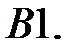Найти ограниченные решения системы
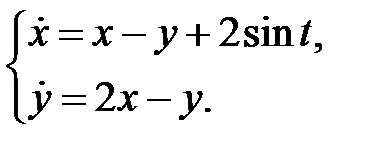
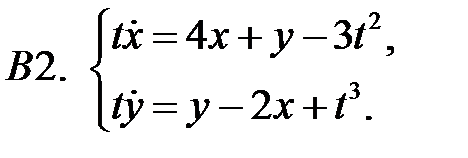
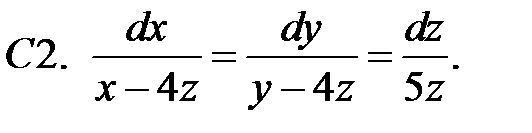
13. 
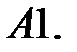
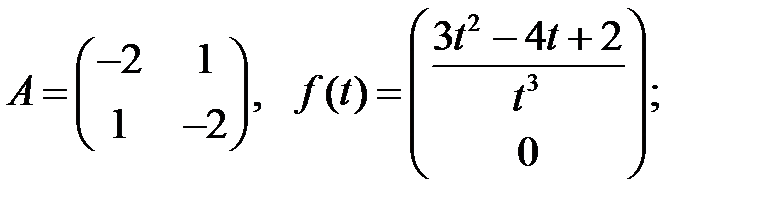
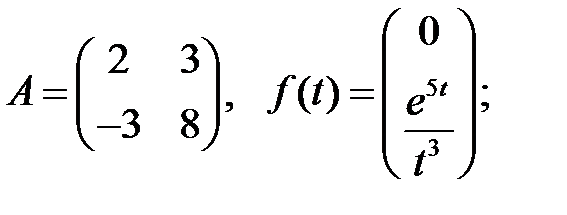
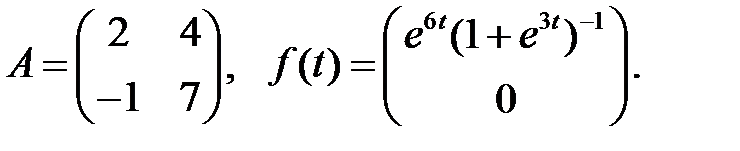
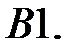Найти периодическое решение системы
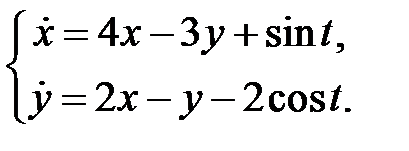
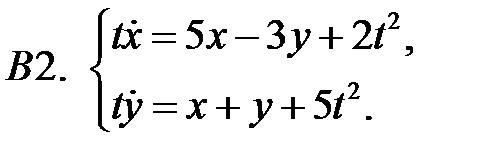
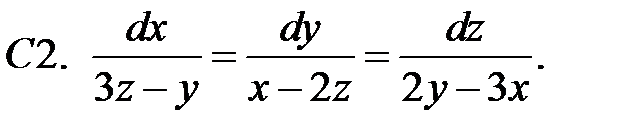
14. 
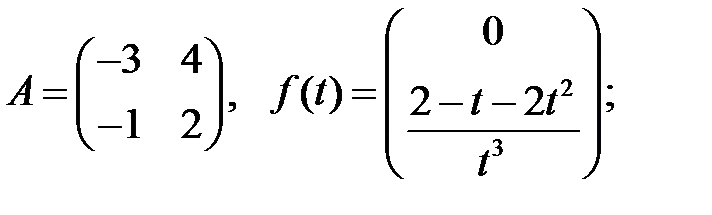
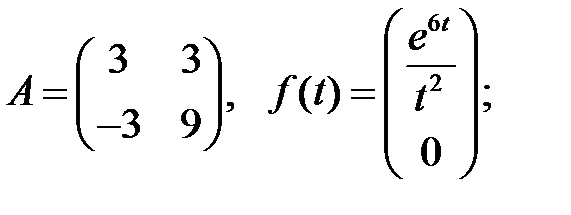
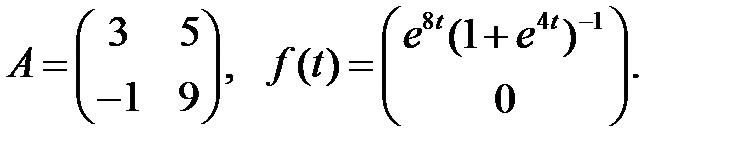
Выяснить, является ли выражение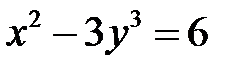 
первым интегралом системы
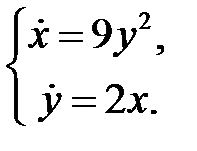
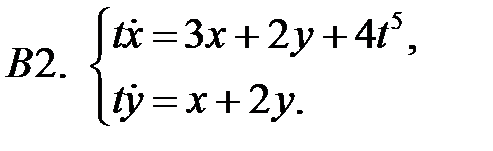
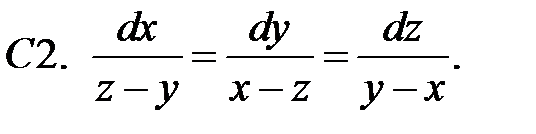
15. 
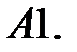
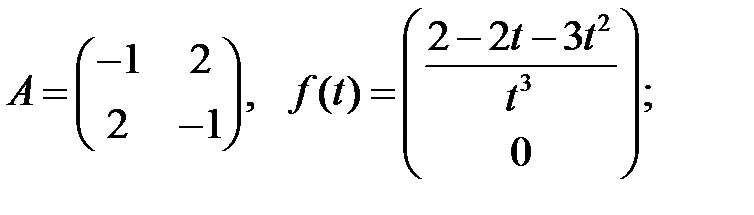
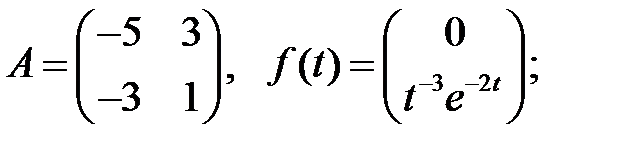
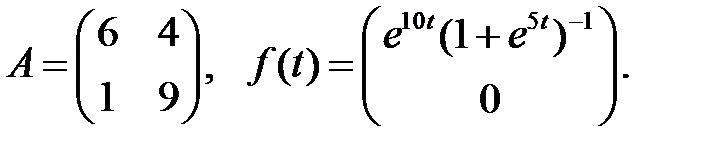
Образуют ли вектор-функции
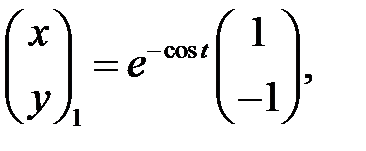
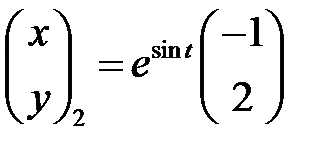
фундаментальную систему решений системы
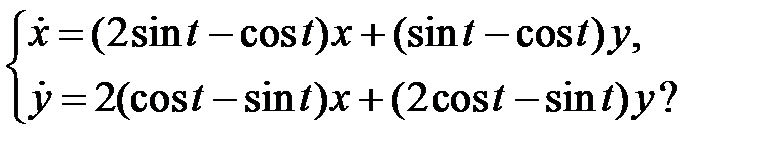
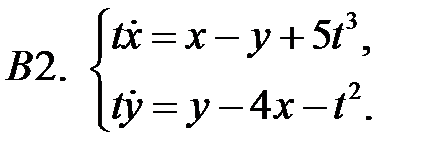
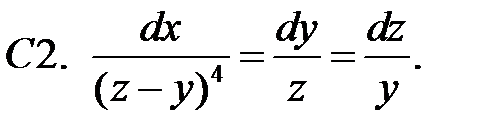
16. 
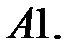
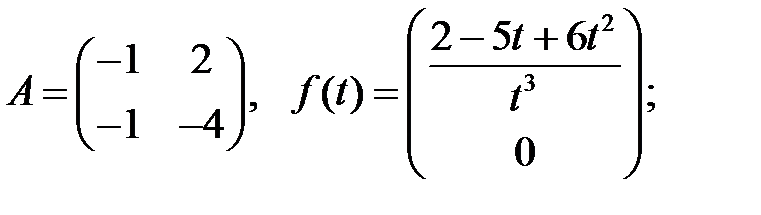
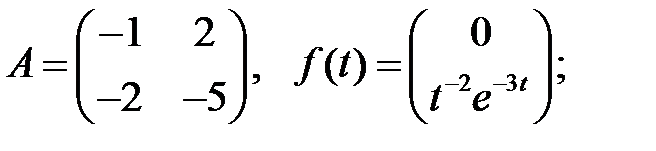
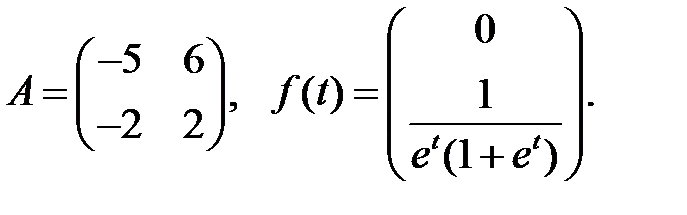
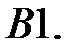Составить линейную однородную систему, имеющую фундаментальную матрицу
.
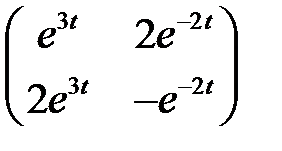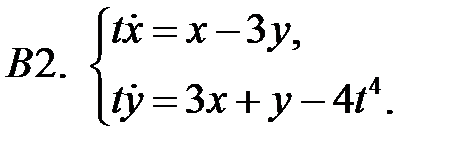
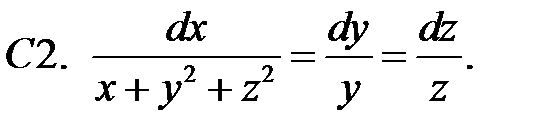
17. 
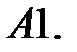
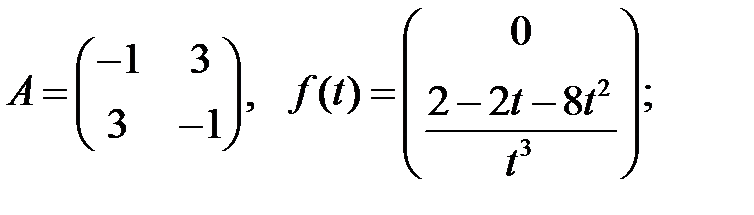
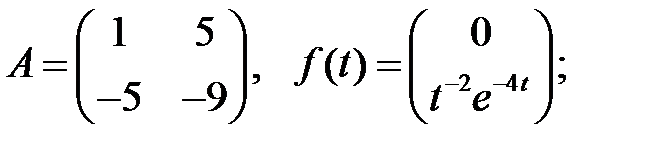
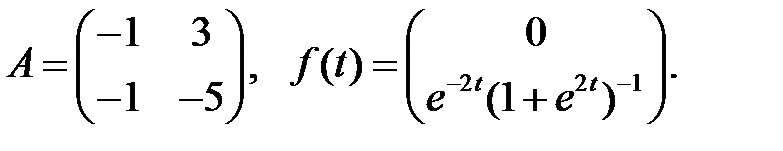
Составить линейную однородную систему, имеющую фундаментальную матрицу
.
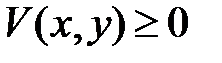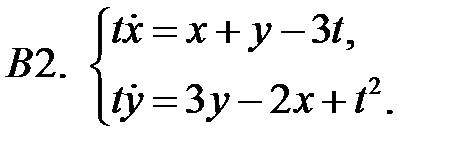
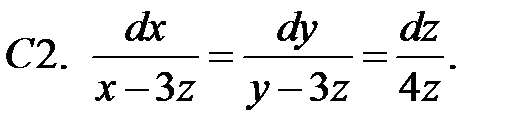
18. 
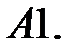
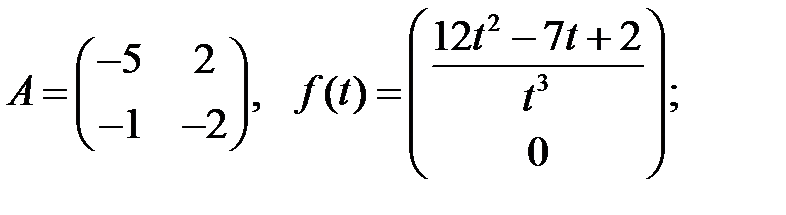
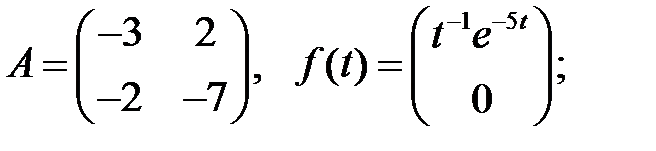
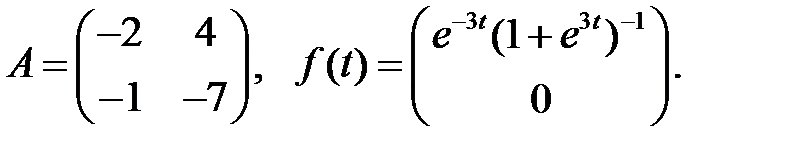
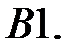Найти неограниченные решения системы
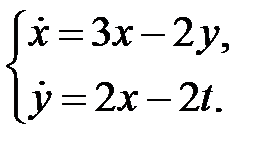
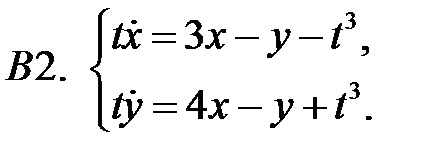
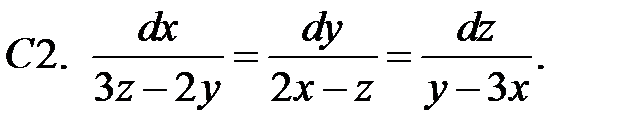
19. 
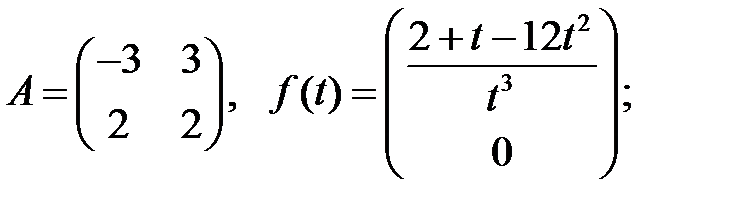
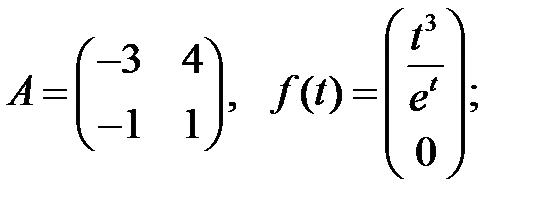
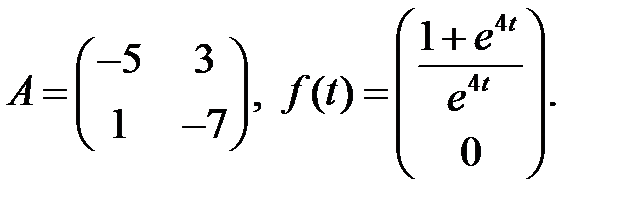
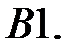Решить систему
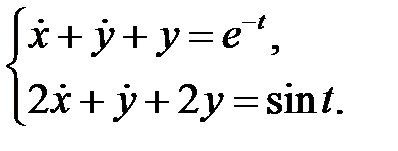
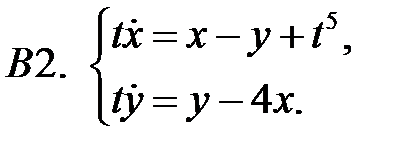
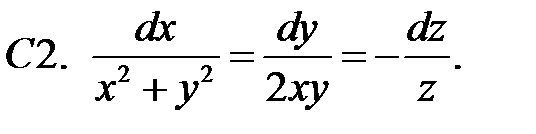
20. 
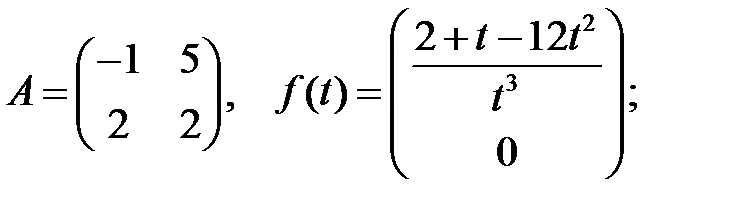
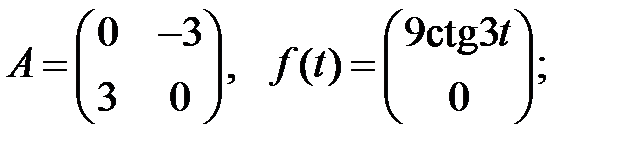
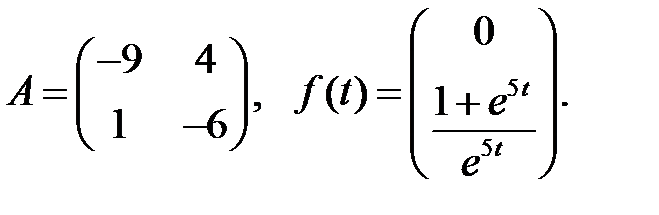
При каких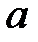 
и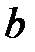 
каждое решение системы
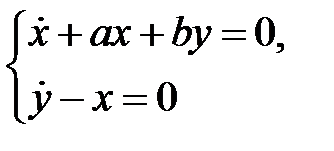
обращается в нуль на бесконечном множестве точек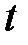 
?
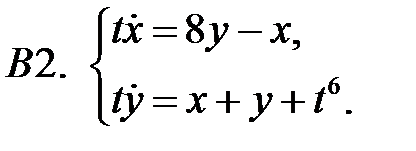
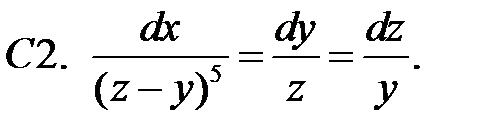
21. 
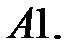
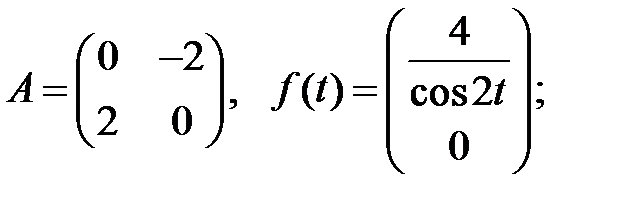
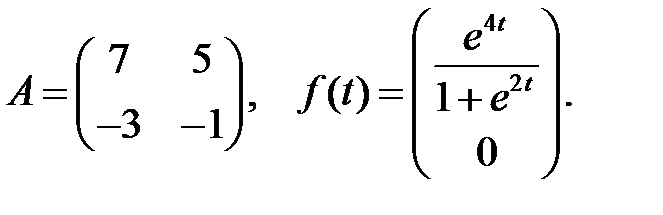
При каких значениях параметра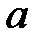 
все решения системы
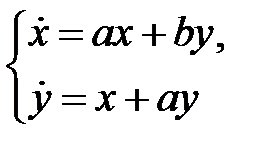
стремятся к нулю 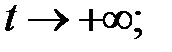при 
при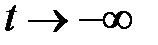 
?
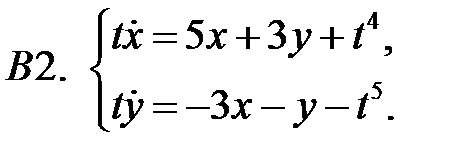
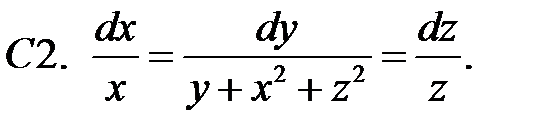
22. 
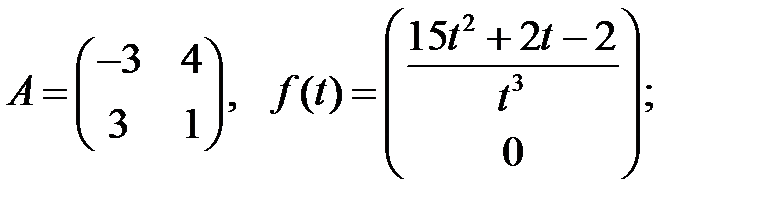
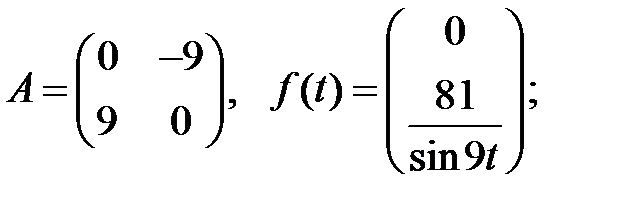
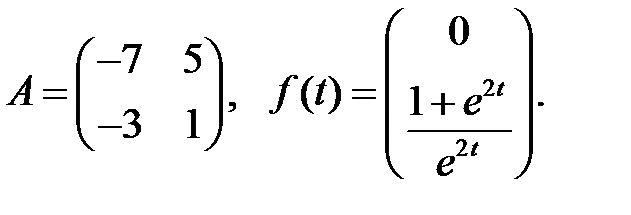
Найти решения системы
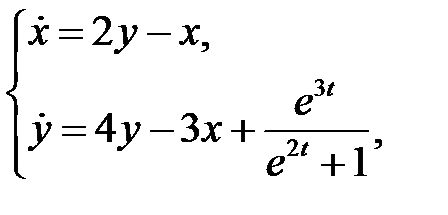
которые остаются ограниченными при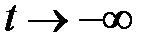 
.
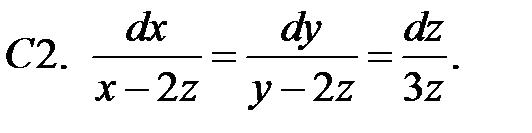
23. 
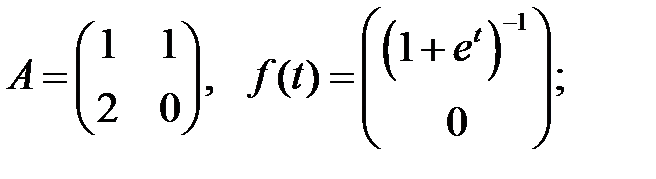
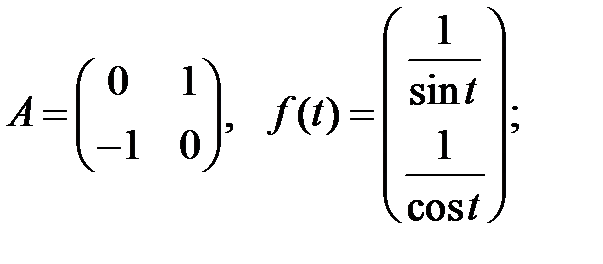
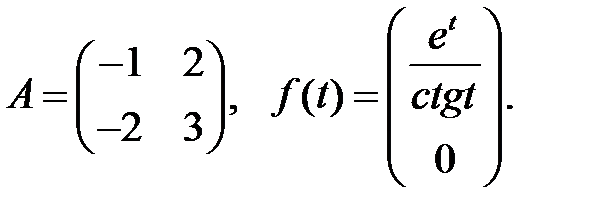
Найти решение системы
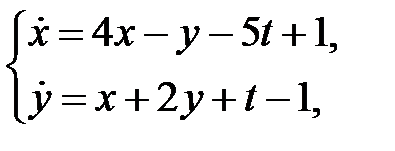
которое стремится к нулю при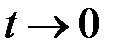 
.
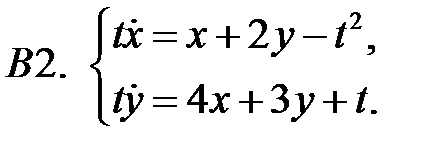
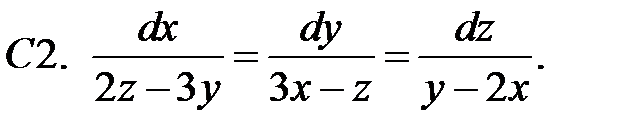
24. 
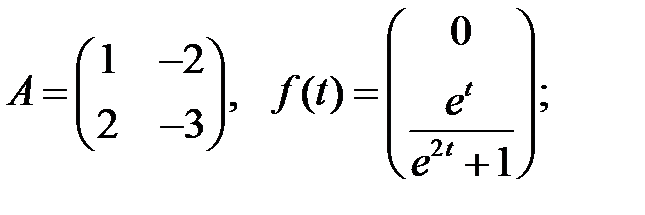
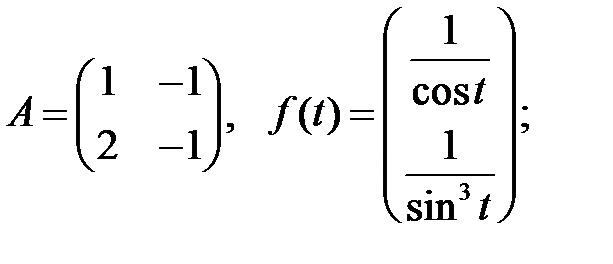
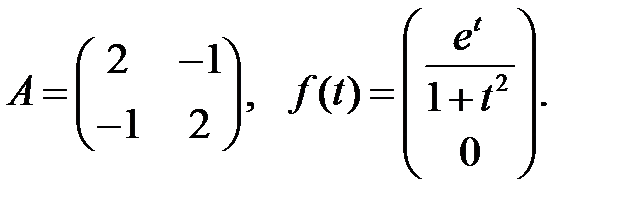
Выяснить, является ли выражение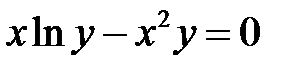 
первым интегралом системы
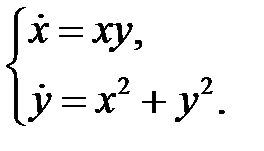
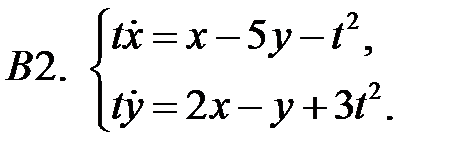
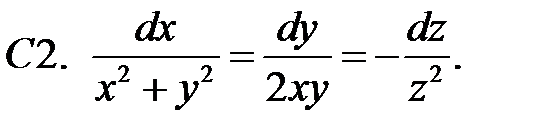
25. 
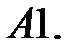
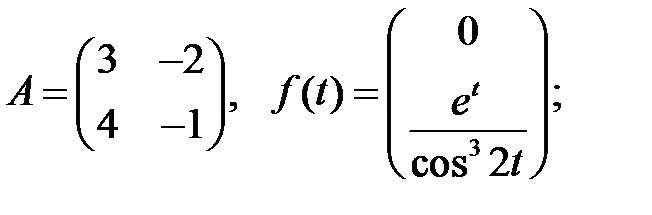
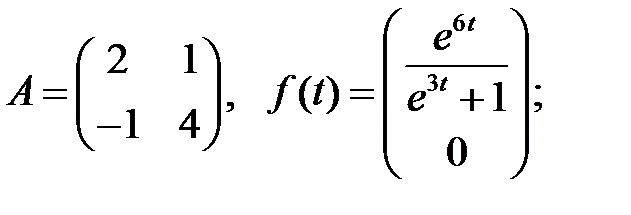
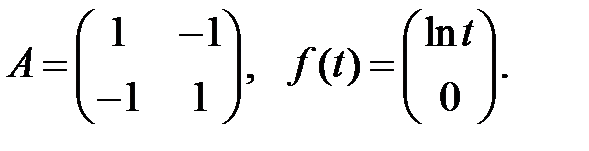
При каких значениях параметров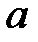 
и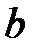 
все решения системы
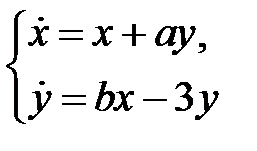
стремятся к нулю 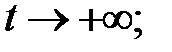при 
при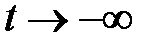 
?
