Общее решение имеет вид
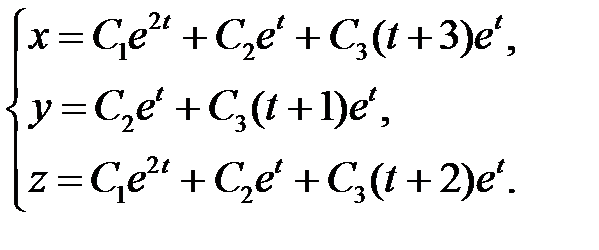
Пример 4. Найти общее решение системы
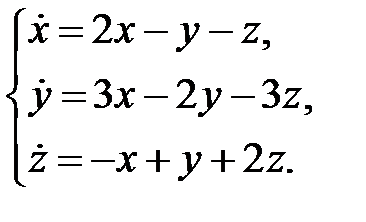
Решение. Характеристическое уравнение
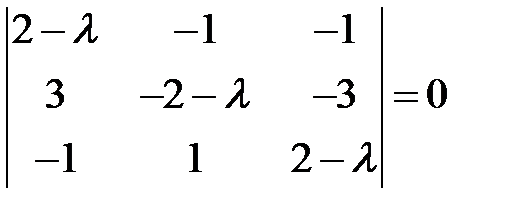 ,
,
имеет корни 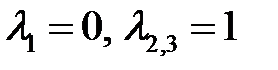 . Найдем собственный вектор, соответствующий корню
. Найдем собственный вектор, соответствующий корню 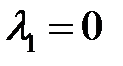 :
:
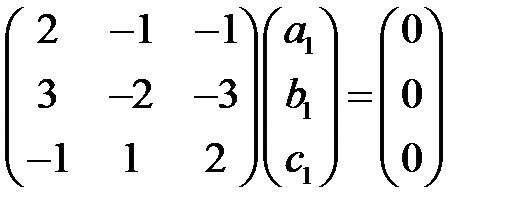 .
.
Отсюда 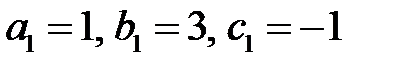 ,
,
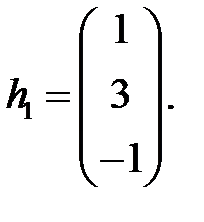
Найдем собственный вектор, соответствующий корню 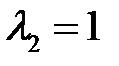 :
:
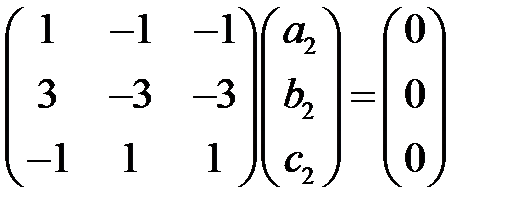 ,
, 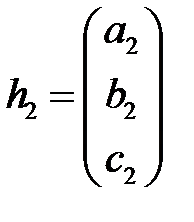 .
.
Так как ранг матрицы 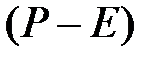 равен 1, то третий собственный вектор
равен 1, то третий собственный вектор 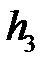 находится так же, как
находится так же, как 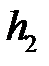 , но надо выбрать его так, чтобы
, но надо выбрать его так, чтобы 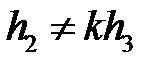 . Мы примем
. Мы примем
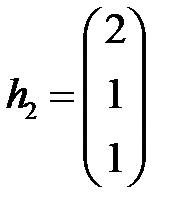 ,
, 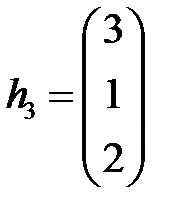 .
.
Тогда общее решение имеет вид
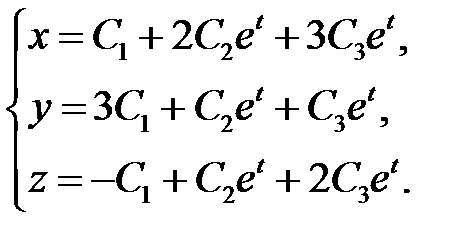
Пример 5. Найти решение задачи Коши
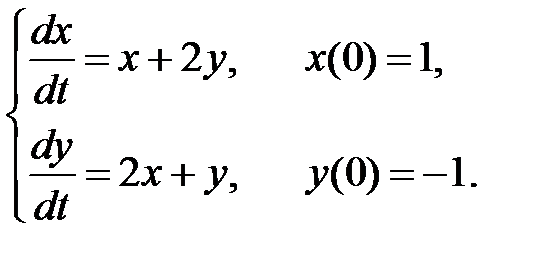
Решение. Запишем матрицу системы
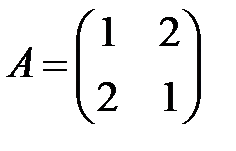 .
.
Характеристическое уравнение
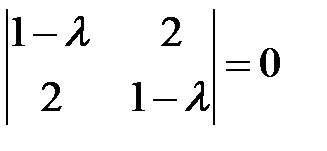
имеет корни 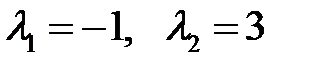 . Для каждого корня (собственного значения матрицы
. Для каждого корня (собственного значения матрицы  ) составим систему уравнений
) составим систему уравнений 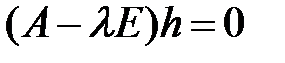 , решив которую, найдем собственный вектор.
, решив которую, найдем собственный вектор.
В случае 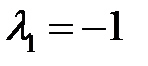 система для определения
система для определения 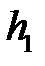 имеет вид
имеет вид
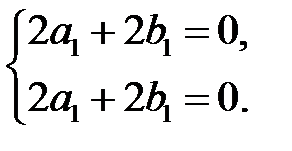
Из этой системы находим: 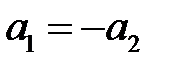 , и, полагая
, и, полагая 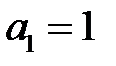 , получаем собственный вектор
, получаем собственный вектор 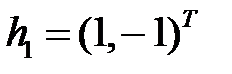 .
.
В случае 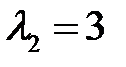 соответствующая система имеет вид
соответствующая система имеет вид
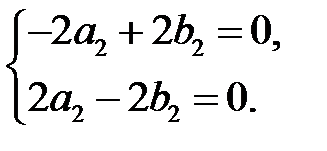
Из этой системы находим: 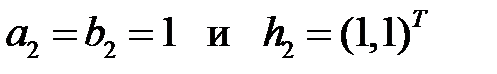 .
.
Запишем общее решение
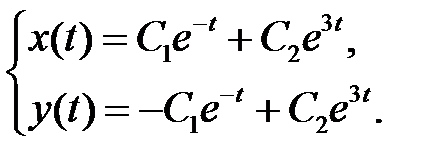
Используя начальные условия, получаем систему
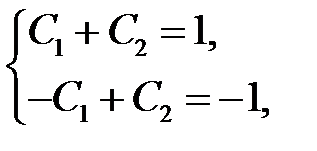
из которой находим 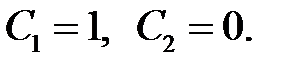 Следовательно, решение рассматриваемой задачи Коши имеет вид
Следовательно, решение рассматриваемой задачи Коши имеет вид
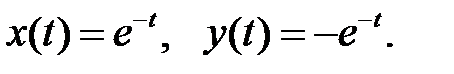
Пример 6. Найти общий интеграл системы
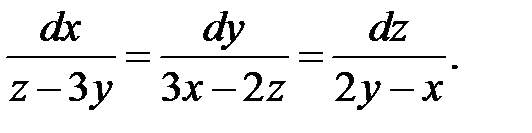
Решение. Построим две интегрируемые комбинации, пользуясь свойством ряда равных отношений. Умножим в системе числители и знаменатели дробей соответственно на 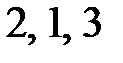 и сложим числители и знаменатели полученных дробей.
и сложим числители и знаменатели полученных дробей.
Тогда
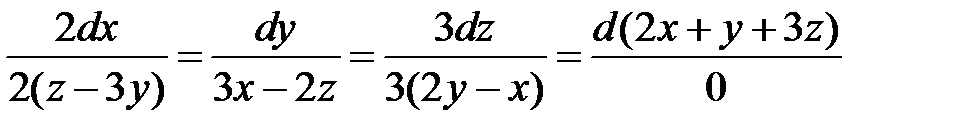 ,
,
откуда
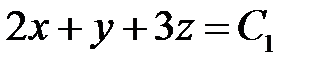 .
.
Теперь умножим в данной системе числители и знаменатели дробей соответственно на 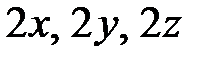 и сложим числители и знаменатели полученных дробей
и сложим числители и знаменатели полученных дробей
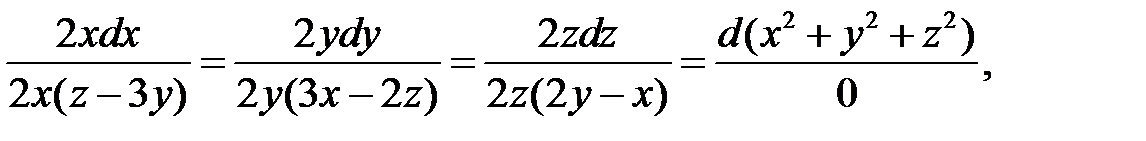
следовательно,
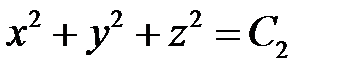 .
.
При этом очевидно, что полученные первые интегралы независимы, так что их совокупность образует общий интеграл исходной системы.
6.2. Линейные неоднородные системы дифференциальных уравнений
с постоянными коэффициентами
Пусть даны система уравнений (1), 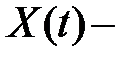 фундаментальная матрица системы уравнений (2),
фундаментальная матрица системы уравнений (2), 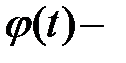 решение системы уравнений (1).
решение системы уравнений (1).
Теорема 2. Общее решение системы уравнений (1) имеет вид
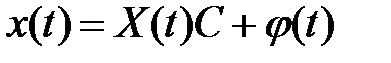 ,
,
где 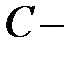 постоянный вектор-столбец.
постоянный вектор-столбец.
Пусть матрица 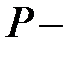 постоянная матрица. Тогда для нахождения частного решения
постоянная матрица. Тогда для нахождения частного решения 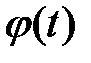 существует два метода: метод Лагранжа (этот метод применим и в общем случае) и метод неопределенных коэффициентов.
существует два метода: метод Лагранжа (этот метод применим и в общем случае) и метод неопределенных коэффициентов.
Метод Лагранжа
Пусть 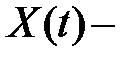 фундаментальная матрица системы уравнений (2) найдена. Тогда
фундаментальная матрица системы уравнений (2) найдена. Тогда 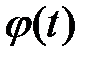 ищем в виде
ищем в виде
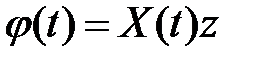 ,
,
где неизвестный вектор 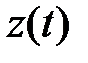 находится из системы уравнений
находится из системы уравнений
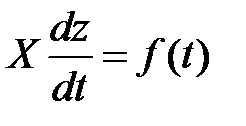 , т.е.
, т.е. 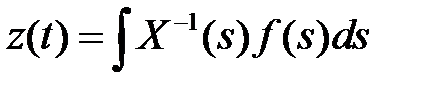 .
.
Метод неопределенных коэффициентов
Пусть 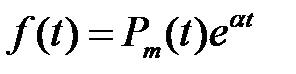 , где
, где 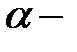 константа,
константа, 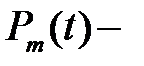 вектор, каждый элемент которого есть многочлен порядка не выше
вектор, каждый элемент которого есть многочлен порядка не выше 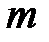 . Тогда частное решение
. Тогда частное решение 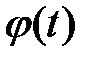 ищем в виде
ищем в виде
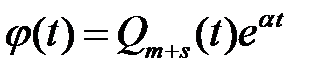 ,
,
где 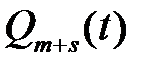 есть многочлен порядка не выше
есть многочлен порядка не выше 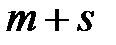 ;
; 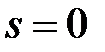 , если
, если 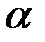 не совпадает с корнем характеристического уравнения;
не совпадает с корнем характеристического уравнения; 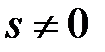 , если
, если 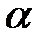 является кратным корнем, при этом
является кратным корнем, при этом 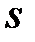 равно кратности этого корня. Коэффициенты многочлена находятся путем сравнения коэффициентов при подобных членах.
равно кратности этого корня. Коэффициенты многочлена находятся путем сравнения коэффициентов при подобных членах.
Аналогично находится частное решение 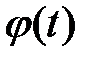 , если
, если
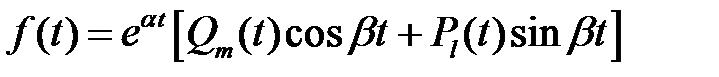 ,
,
при этом для определения 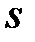 сравнивают число
сравнивают число 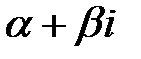 с корнями характеристического уравнения.
с корнями характеристического уравнения.
Пример 7. Решить систему
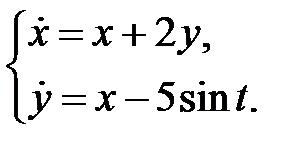
Решение. Общее решение однородной системы уравнений имеет вид
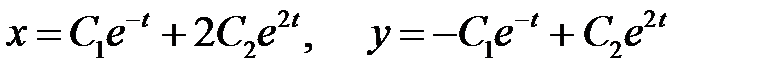 .
.
Так как 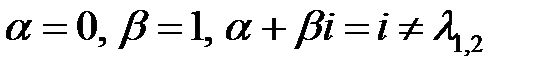 , то частное решение ищем так:
, то частное решение ищем так:
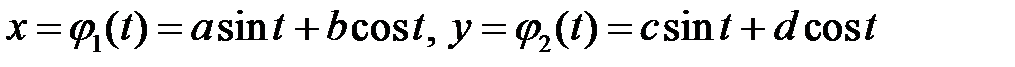 .
.
Подставляя 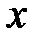 и
и 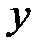 в систему уравнений и сравнивая коэффициенты, имеем
в систему уравнений и сравнивая коэффициенты, имеем
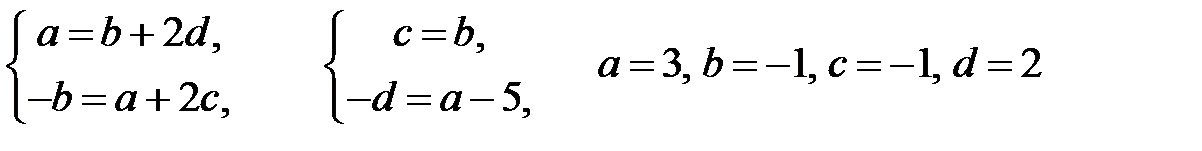 .
.
Общее решение имеет вид
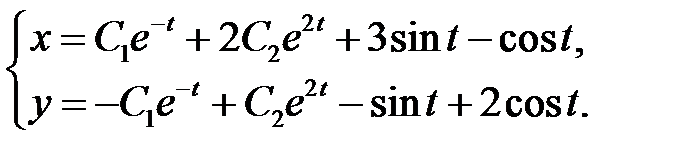
Пример 8.Найти общее решение системы
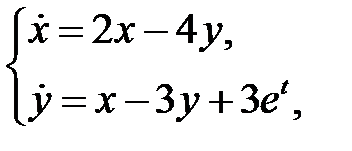
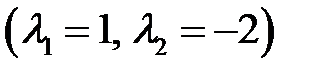 .
.
Решение. Общее решение однородной системы уравнений представим так:
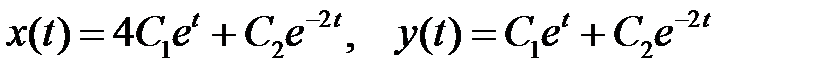 .
.
Число 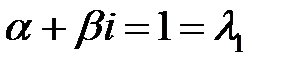 . Поэтому ищем частное решение в виде
. Поэтому ищем частное решение в виде
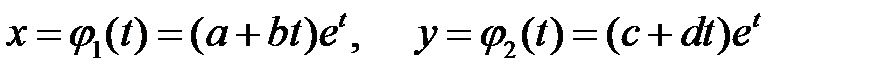 .
.
Подставив 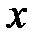 и
и 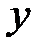 в левую и правую части системы уравнений, найдем постоянные
в левую и правую части системы уравнений, найдем постоянные  . Общее решение имеет вид
. Общее решение имеет вид
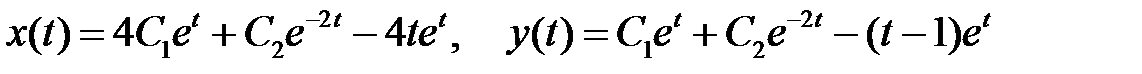 .
.
Пример 9. Найти общее решение системы:
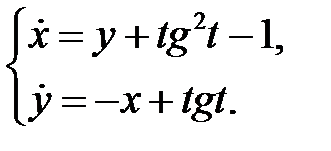
Решение. Найдем фундаментальную матрицу:
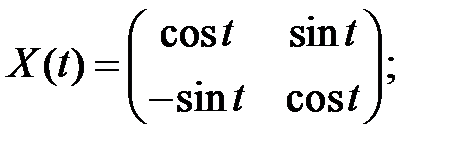
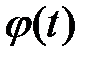 ищем в виде
ищем в виде
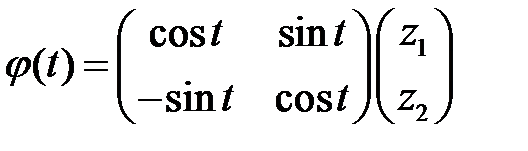 .
.
Тогда
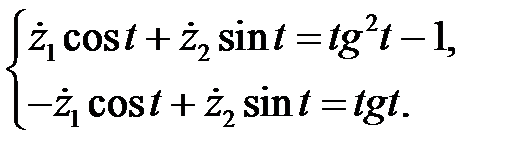
Решая эту систему и интегрируя, найдем
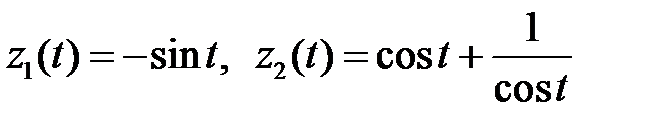 .
.
Подставляя результаты в вектор 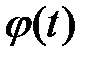 , получим
, получим
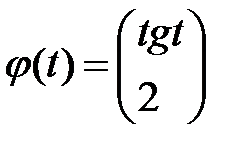 .
.
Поэтому функции
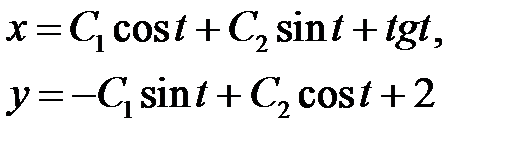
будут общим решением исходной системы.
Пример 10. Найти общее решение системы
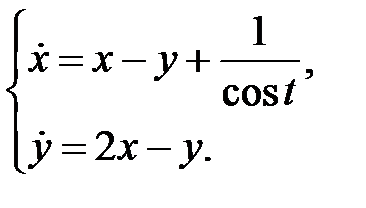
Решение. Собственные числа матрицы
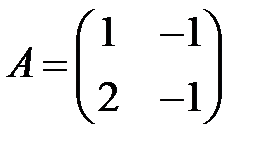
равны 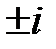 , а фундаментальная матрица имеет вид
, а фундаментальная матрица имеет вид
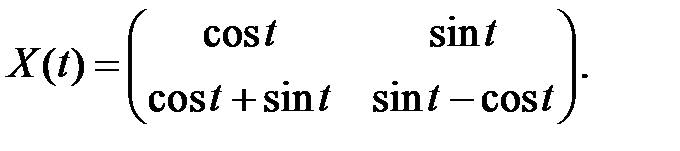
Частное решение ищем в виде
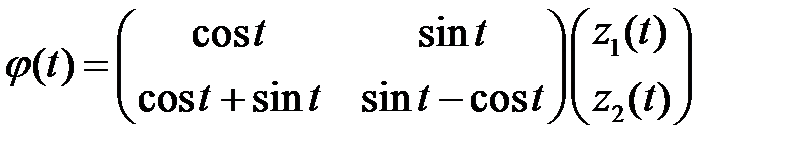 . (*)
. (*)
Для определения 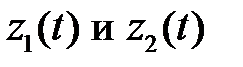 получим систему
получим систему
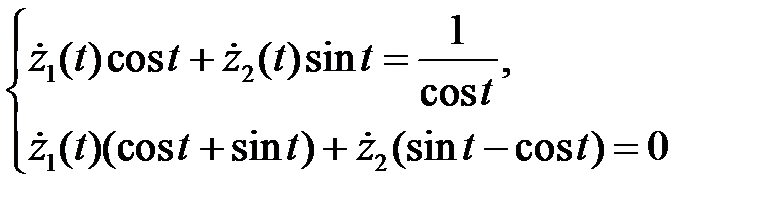
Решая эту систему и интегрируя, найдем
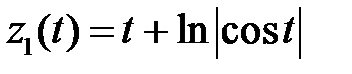 ,
, 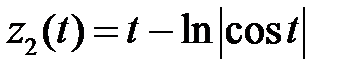 .
.
Подставляя в (*), получим частное решение
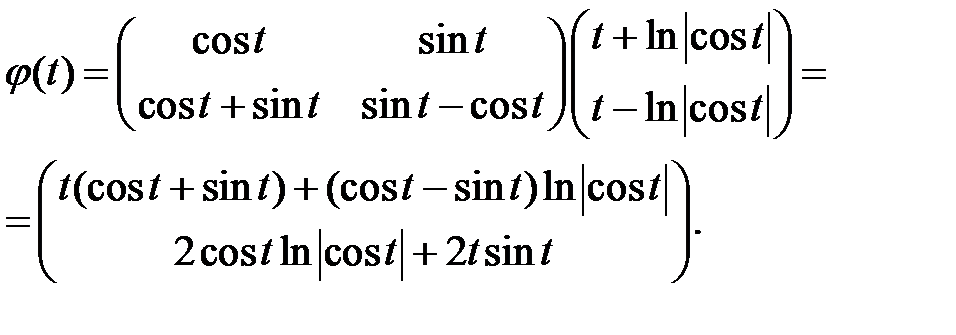
Следовательно, общее решение запишется в следующем виде
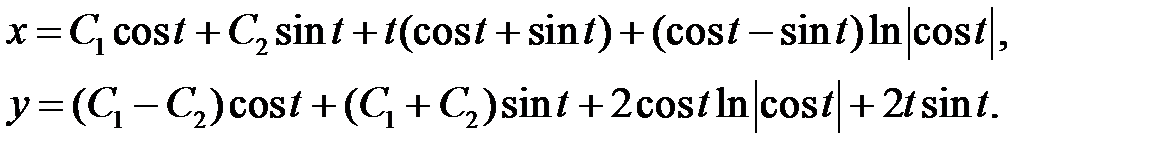
Пример 11. Найти общее решение системы
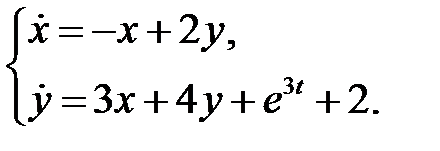
Решение. Собственные числа линейной однородной системы равны 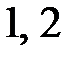 . Собственные векторы, отвечающие этим собственным числам, равны соответственно
. Собственные векторы, отвечающие этим собственным числам, равны соответственно
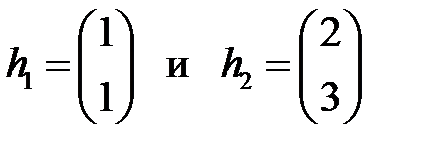 .
.
Тогда частные решения ищем в виде
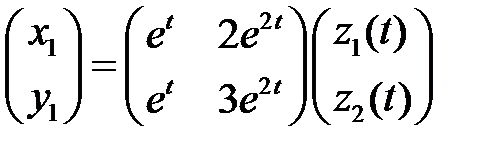 .
.
Подставляя в исходную систему, получим
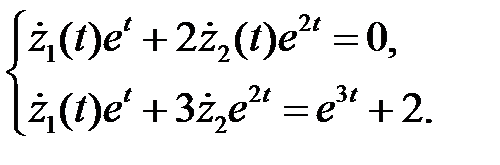
Решая эту систему, находим
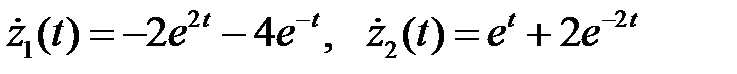 .
.
Проинтегрировав, имеем
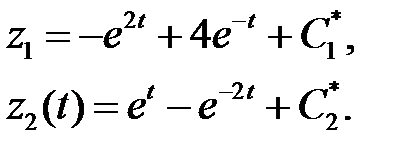
Таким образом, общее решение исходной системы имеет вид
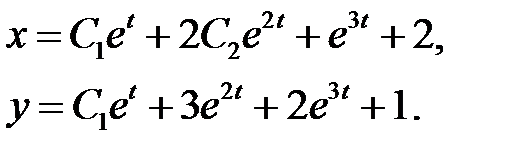
6.3. Устойчивость по Ляпунову
Дана вектор-функция 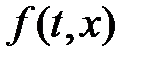 , непрерывно дифференцируемая
, непрерывно дифференцируемая 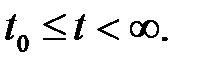 Рассмотрим систему уравнений в векторной записи
Рассмотрим систему уравнений в векторной записи
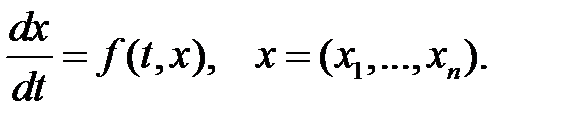 (4)
(4)
Решение 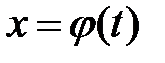 системы (4) называется устойчивым по Ляпунову, если для любого
системы (4) называется устойчивым по Ляпунову, если для любого 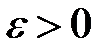 существует такое
существует такое 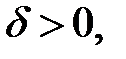 что для всякого решения
что для всякого решения 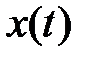 той же системы, начальное значение которого удовлетворяет неравенству
той же системы, начальное значение которого удовлетворяет неравенству
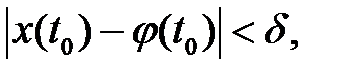 (*)
(*)
при всех 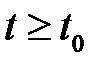 выполняется неравенство
выполняется неравенство
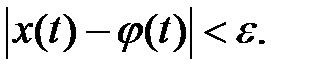
Если же для некоторого 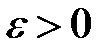 такого
такого 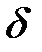 не существует, то решение
не существует, то решение 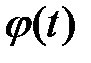 называется неустойчивым.
называется неустойчивым.
Решение 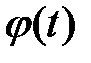 называется асимптотически устойчивым, если оно устойчиво по Ляпунову и, кроме того, все решения с достаточно близкими начальными условиями неограниченно приближаются к
называется асимптотически устойчивым, если оно устойчиво по Ляпунову и, кроме того, все решения с достаточно близкими начальными условиями неограниченно приближаются к 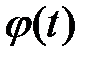 при
при 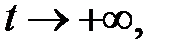 т.е. если из неравенства (*) следует
т.е. если из неравенства (*) следует 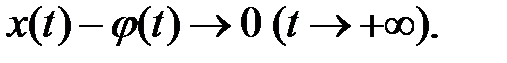
Наличие или отсутствие устойчивости не зависит от выбора 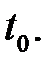
Теорема 3. Если все собственные числа матрицы 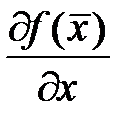 системы (4) имеют отрицательные вещественные части, то решение
системы (4) имеют отрицательные вещественные части, то решение 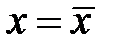 системы (1) асимптотически устойчиво.
системы (1) асимптотически устойчиво.
Теорема 4. Если хотя бы одно из собственных чисел матрицы 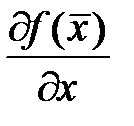 системы (4) имеет положительную вещественную часть, то решение
системы (4) имеет положительную вещественную часть, то решение 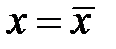 неустойчиво.
неустойчиво.
Пример 12. Исследовать на устойчивость нулевое решение системы
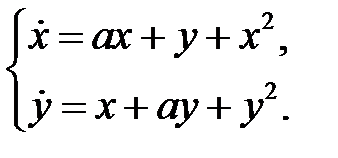
Решение. Находим собственные значения матрицы коэффициентов
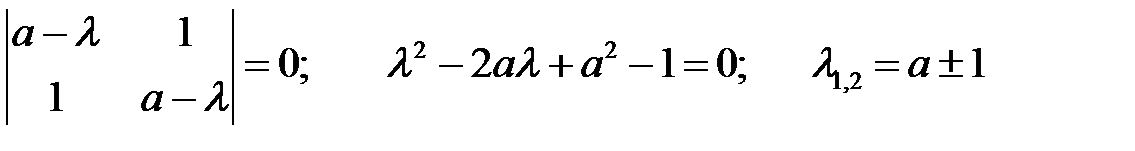 .
.
При 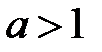 оба корня положительны, а при
оба корня положительны, а при 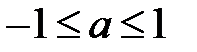 один корень положителен, значит, в этих случаях нулевое решение неустойчиво.
один корень положителен, значит, в этих случаях нулевое решение неустойчиво.
При 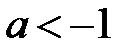 корни вещественны, отрицательны, значит, нулевое решение асимптотически устойчиво.
корни вещественны, отрицательны, значит, нулевое решение асимптотически устойчиво.
При 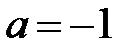 вопрос об устойчивости не решается с помощью теорем 3 и 4.
вопрос об устойчивости не решается с помощью теорем 3 и 4.
Устойчивость или неустойчивость решений линейной однородной системы с постоянными коэффициентами
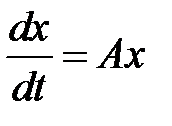
исследуется проще и определяется собственными числами матрицы 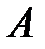 .
.
Теорема 5. Решения линейной однородной системы дифференциальных уравнений с постоянными коэффициентами тогда и только тогда являются:
1. устойчивыми, когда действительные части собственных чисел матрицы системы неположительные, причем числам с нулевой действительной частью соответствуют одномерные клетки Жордана в жордановой форме матрицы, т.е. таким числам соответствуют простые элементарные делители;
2. асимптотически устойчивыми, когда действительные части собственных чисел матрицы системы отрицательны;
3. неустойчивыми, когда хотя бы одному собственному числу с нулевой действительной частью соответствует неодномерная клетка Жордана (такому числу соответствует непростой элементарный делитель), либо когда среди собственных чисел матрицы системы имеется хотя бы одно число с положительной действительной частью.
Замечание. Решения линейной однородной системы с постоянными коэффициентами либо все одновременно устойчивы, либо неустойчивы.
Пример 13. Исследовать на устойчивость решения системы уравнений
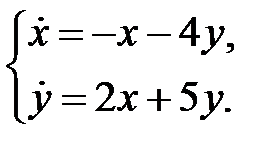
Решение. Собственные числа матрицы данной системы определяем из уравнения
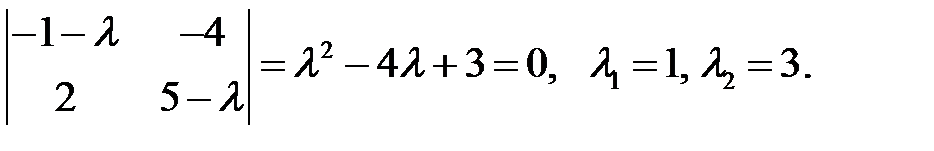
Эти числа действительные и положительные, значит все решения системы неустойчивы.
Рассмотрим систему дифференциальных уравнений
 , (5)
, (5)
в которой  - постоянная матрица,
- постоянная матрица, 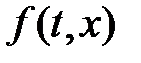 - непрерывная по
- непрерывная по 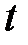 и непрерывно дифференцируемая по
и непрерывно дифференцируемая по 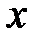
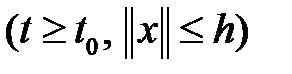 функция, удовлетворяющая условию
функция, удовлетворяющая условию
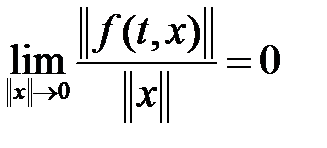 (6)
(6)
равномерно по 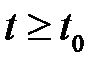 . Система уравнений с постоянными коэффициентами
. Система уравнений с постоянными коэффициентами
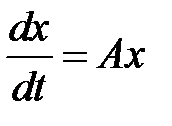
называется системой первого приближения для системы (5).
Теорема 6. Если действительные части всех собственных чисел матрицы 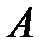 отрицательны, а функция
отрицательны, а функция 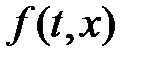 удовлетворяет равенству (6), то нулевое решение системы уравнений (5) асимптотически устойчиво. Если же среди собственных чисел матрицы имеется хотя бы одно число с положительной действительной частью, то нулевое решение системы уравнений (5) неустойчиво.
удовлетворяет равенству (6), то нулевое решение системы уравнений (5) асимптотически устойчиво. Если же среди собственных чисел матрицы имеется хотя бы одно число с положительной действительной частью, то нулевое решение системы уравнений (5) неустойчиво.
Если же среди собственных чисел матрицы 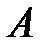 имеется хотя бы одно с нулевой действительной частью, а остальные – с отрицательной, то нулевое решение системы уравнений (5) может быть как устойчивым (асимптотически устойчивым), так и неустойчивым, т.е. в этом случае из устойчивости решений системы первого приближения нельзя делать вывод об устойчивости тривиального решения полной системы уравнений.
имеется хотя бы одно с нулевой действительной частью, а остальные – с отрицательной, то нулевое решение системы уравнений (5) может быть как устойчивым (асимптотически устойчивым), так и неустойчивым, т.е. в этом случае из устойчивости решений системы первого приближения нельзя делать вывод об устойчивости тривиального решения полной системы уравнений.
Пример 14. С помощью теоремы Ляпунова об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы
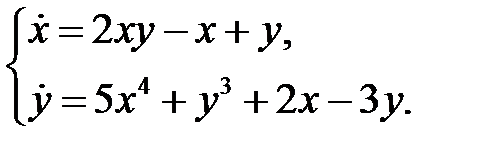
Решение. Запишем систему первого приближения
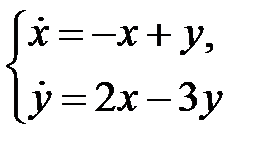
и соответствующее им характеристическое уравнение
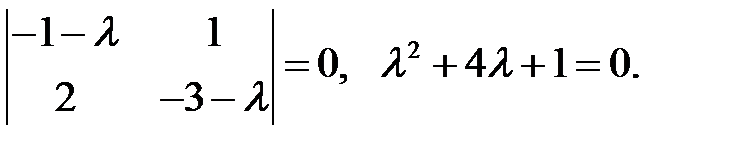
Корни характеристического уравнения 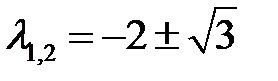 действительны и отрицательны, таким образом, нулевое решение исходной системы асимптотически устойчиво.
действительны и отрицательны, таким образом, нулевое решение исходной системы асимптотически устойчиво.
Пример 15. С помощью теоремы Ляпунова об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы
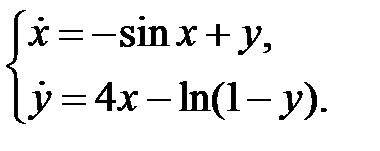
Решение. Учитывая разложения
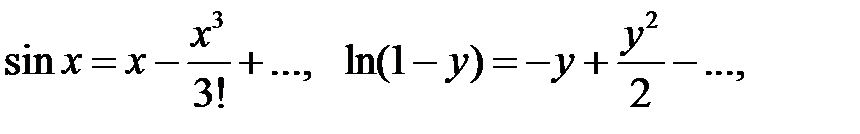
запишем систему первого приближения и составим характеристическое уравнение
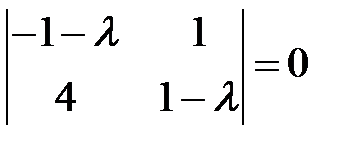 ,
, 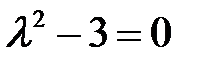 ,
,
корни которого равны 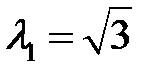 ,
, 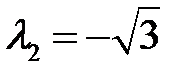 . Следовательно, по теореме Ляпунова нулевое решение неустойчиво.
. Следовательно, по теореме Ляпунова нулевое решение неустойчиво.
6.4. Особые точки на плоскости
Рассмотрим задачу о расположении траекторий (т.е. проекций на плоскости 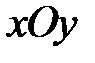 графиков решений
графиков решений 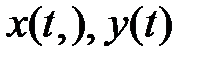 ) системы
) системы
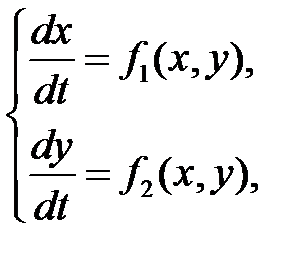 (7)
(7)
где 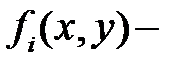 непрерывно дифференцируемые функции в окрестности состояний равновесия, т.е. в точках, где
непрерывно дифференцируемые функции в окрестности состояний равновесия, т.е. в точках, где 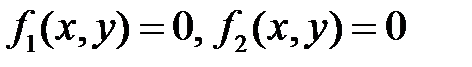 . Пусть точка
. Пусть точка 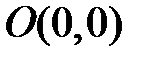 есть состояние равновесия. Для исследования этой точки представим систему (7) в виде
есть состояние равновесия. Для исследования этой точки представим систему (7) в виде
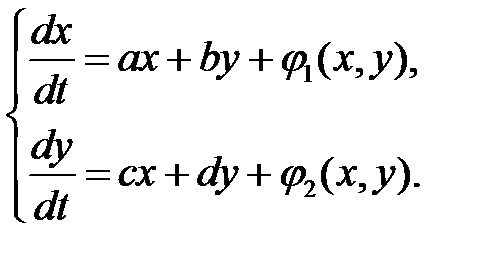 (8)
(8)
Рассмотрим случай, когда система (8) является линейной однородной, т. е. имеет вид
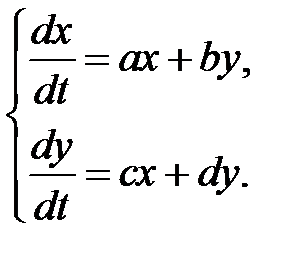 (9)
(9)
Все возможные картины расположения траекторий получаются неособыми линейными преобразованиями плоскости. Пусть 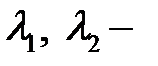 собственные числа матрицы
собственные числа матрицы 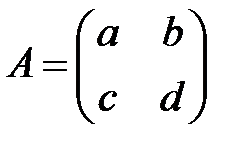 . Если корни вещественные, различные и одного знака, то особая точка – узел; если разных знаков – седло; если корни комплексные
. Если корни вещественные, различные и одного знака, то особая точка – узел; если разных знаков – седло; если корни комплексные 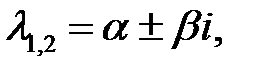
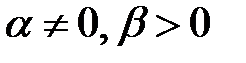 , то особая точка – фокус, а если
, то особая точка – фокус, а если 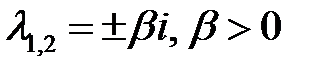 , то – центр. Если корни равные и ненулевые, то различают два случая:
, то – центр. Если корни равные и ненулевые, то различают два случая:
1. 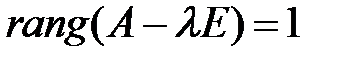 ; 2.
; 2. 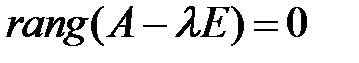 .
.
В первом случае, особую точку называют вырожденным узлом, а во втором случае – дикритическим узлом.
Полная классификация всех возможных случаев приведена в таблице.
Чтобы начертить траектории системы (9) в случае узла, седла и вырожденного узла, надо прежде всего найти те решения, которые изображаются прямыми, проходящими через особую точку. Эти прямые всегда направлены вдоль собственных векторов матрицы 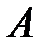 . В случае узла кривые касаются той прямой, которая направлена вдоль собственного вектора, соответствующего меньшему по абсолютной величине значению
. В случае узла кривые касаются той прямой, которая направлена вдоль собственного вектора, соответствующего меньшему по абсолютной величине значению 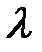 .
.
Направление движения точки 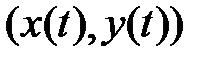 по всем траекториям при возрастании
по всем траекториям при возрастании 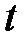 определяется в случае узлов и фокуса знаком
определяется в случае узлов и фокуса знаком 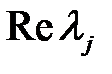 : если
: если 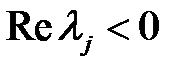 , то движение к точке
, то движение к точке 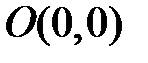 . В случае седла направление движения точки
. В случае седла направление движения точки 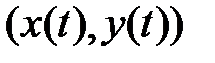 по траекториям, лежащим на одной из прямых, проходящих через начало координат, - к точке
по траекториям, лежащим на одной из прямых, проходящих через начало координат, - к точке 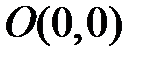 , а на другой – от точки
, а на другой – от точки 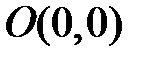 .
.
Для любой точки 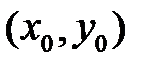 скорость ее движения по траектории вычисляется подстановкой
скорость ее движения по траектории вычисляется подстановкой 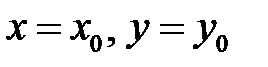 в правую часть системы (9):
в правую часть системы (9):
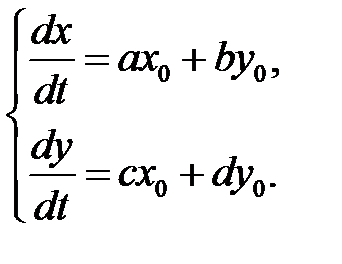
| Корни характеристического уравнения | Название особой точки | Фазовый портрет | ||
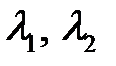 – вещественные, различные и одного знака – вещественные, различные и одного знака
| Узел |
| ||
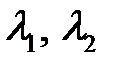 – вещественные, различные и разных знаков – вещественные, различные и разных знаков
| Седло |
| ||
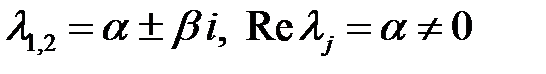
| Фокус |
| ||
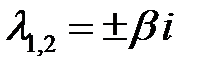
| Центр |
| ||
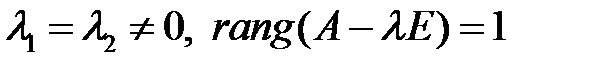
| Вырожденный узел |
| ||
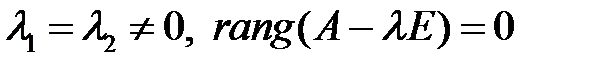
| Дикритический узел |
|
Теперь предположим, что в системе (8) 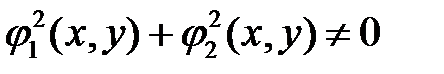 и для некоторого
и для некоторого 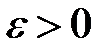
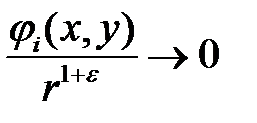 при
при 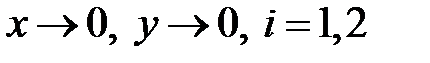 , где
, где 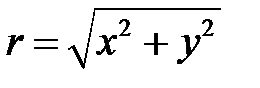 . Если вещественные части всех корней характеристического уравнения отличны от нуля, то особая точка
. Если вещественные части всех корней характеристического уравнения отличны от нуля, то особая точка 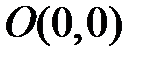 системы (8) будет того же типа, что и особая точка
системы (8) будет того же типа, что и особая точка 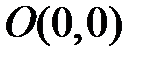 системы (9). Заметим, что угловые коэффициенты направлений траекторий, входящих в особую точку, для систем (8) и (9) одни и те же, а в случае фокуса – направление закручивания одно и то же. В том случае, когда для системы (9) особая точка – центр, для системы (8) она будет либо фокусом, либо центром, либо центрофокусом. В этом случае требуется дополнительное исследование системы (8).
системы (9). Заметим, что угловые коэффициенты направлений траекторий, входящих в особую точку, для систем (8) и (9) одни и те же, а в случае фокуса – направление закручивания одно и то же. В том случае, когда для системы (9) особая точка – центр, для системы (8) она будет либо фокусом, либо центром, либо центрофокусом. В этом случае требуется дополнительное исследование системы (8).
Если же точка 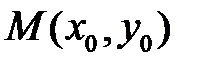 , где
, где 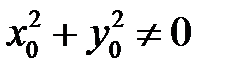 , есть состояние равновесия, то эту систему приводим к виду
, есть состояние равновесия, то эту систему приводим к виду
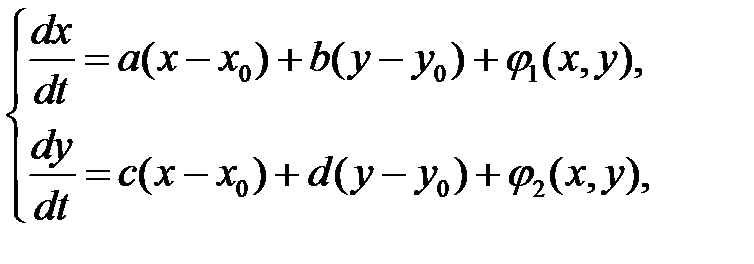 (10)
(10)
где
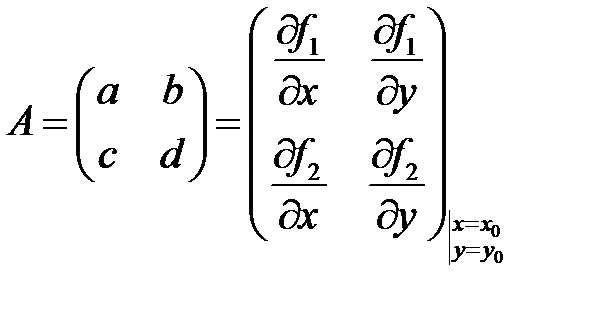 .
.
Расположение траекторий системы (10) совпадает топологически с расположением траекторий соответствующей линейной системы в окрестности точки 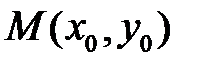 , если
, если 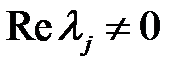 .
.
В примерах 17-18 исследовать особую точку 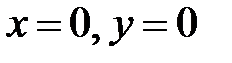 данных систем.
данных систем.
Пример 17.
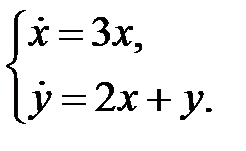
Решение. Составим характеристическое уравнение
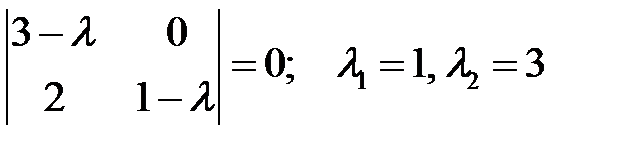 .
.
Корни вещественные, различные и одного знака. Следовательно,  - узел, причем неустойчивый, т.к.
- узел, причем неустойчивый, т.к.  . Для
. Для 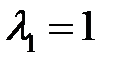 находим собственный вектор
находим собственный вектор 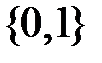 , а для
, а для 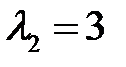 – вектор
– вектор 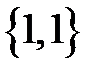 . На плоскости
. На плоскости  строим прямые, направленные вдоль этих векторов:
строим прямые, направленные вдоль этих векторов: 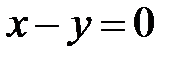 и
и 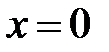 . Каждая из этих прямых содержит три фазовые кривые: состояние равновесия и две полупрямые, на которые разделяется прямая точкой
. Каждая из этих прямых содержит три фазовые кривые: состояние равновесия и две полупрямые, на которые разделяется прямая точкой  . Остальные фазовые кривые касаются при подходе к точке
. Остальные фазовые кривые касаются при подходе к точке 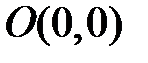 прямой
прямой 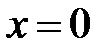 , т.к.
, т.к. 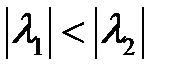 (рис. 1).
(рис. 1).
| x |
| y |
| O |
Рис. 1
Пример 18.
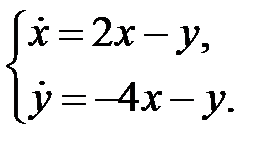
Решение. Собственные числа матрицы 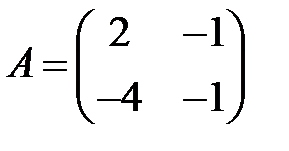 равны
равны 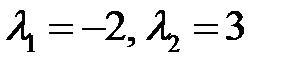 . Следовательно, особая точка
. Следовательно, особая точка  – седло. Для
– седло. Для 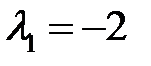 находим собственный вектор
находим собственный вектор 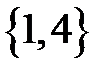 , а для
, а для 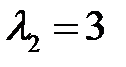 вектор
вектор 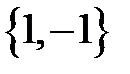 .
.
На прямой 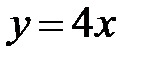 исходная система имеет вид:
исходная система имеет вид:
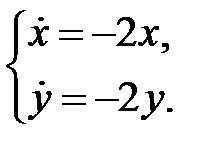
Значит, вдоль прямой 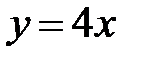 фазовая точка
фазовая точка 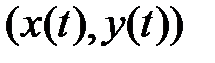 движется по закону:
движется по закону: 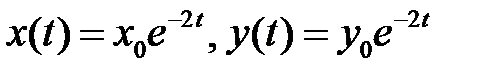 , т.е. движение точки с ростом времени
, т.е. движение точки с ростом времени 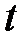 происходит по направлению к началу координат.
происходит по направлению к началу координат.
Аналогично находим, что вдоль прямой 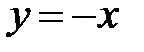 фазовая точка движется согласно системе уравнений
фазовая точка движется согласно системе уравнений
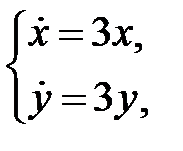
т.е. по закону 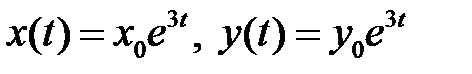 . По этой прямой движение происходит в направлении от начала координат.
. По этой прямой движение происходит в направлении от начала координат.
Схематически траектории исходной системы изображены на рис.2.
| O |
Рис. 2
Пример 19.
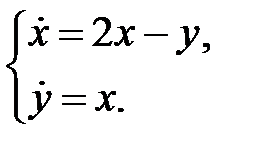
Решение. Составляем и решаем характеристическое уравнение:
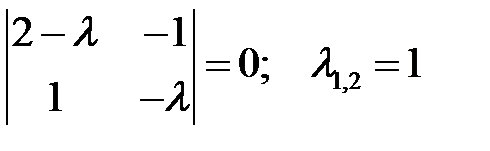 .
.
Корни вещественные и равные, следовательно, 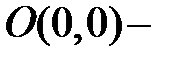 вырожденный узел, причем неустойчивый. Для
вырожденный узел, причем неустойчивый. Для 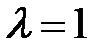 находим собственный вектор
находим собственный вектор 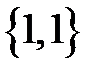 . Остальные фазовые кривые строятся с помощью изоклин (рис.3).
. Остальные фазовые кривые строятся с помощью изоклин (рис.3).
| x |
| y |
| O |
Рис. 3
Пример 20.
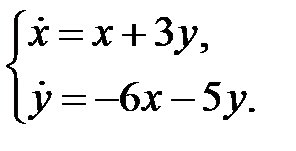
Решение. Находим корни характеристического уравнения:
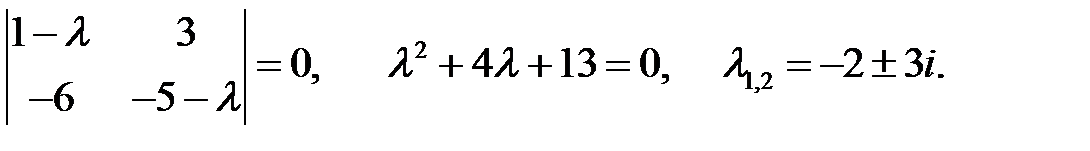
Особая точка – фокус. Строим в точке 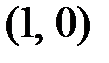 вектор скорости
вектор скорости
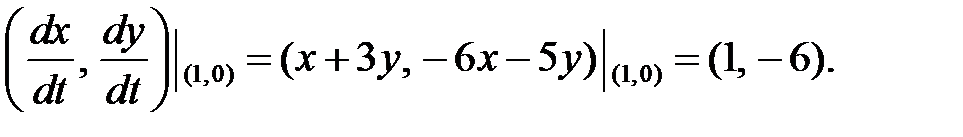
Следовательно, возрастанию 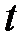 соответствует движение по траекториям по часовой стрелке. Так как вещественная часть корней характеристического уравнения равна
соответствует движение по траекториям по часовой стрелке. Так как вещественная часть корней характеристического уравнения равна 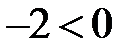 , то особая точка асимптотически устойчива, следовательно, при возрастании
, то особая точка асимптотически устойчива, следовательно, при возрастании 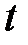 решения неограниченно приближаются к особой точке (рис. 4).
решения неограниченно приближаются к особой точке (рис. 4).
Пример 21. Найти и исследовать особые точки системы
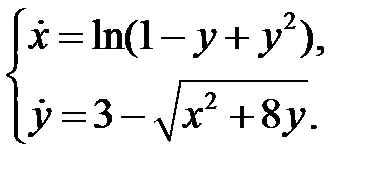
Решение. Найдем состояние равновесия из системы уравнений
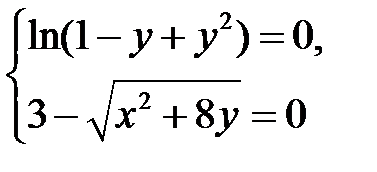 или
или 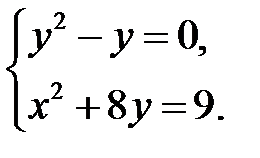
| y |
| x |
| O |
Рис. 4
Система имеет четыре особые точки: 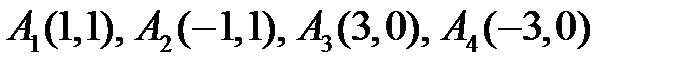 . Для исследования этих особых точек надо перенести начало координат в исследуемую особую точку и разложить правые части уравнений по формуле Тейлора, ограничиваясь членами первого порядка:
. Для исследования этих особых точек надо перенести начало координат в исследуемую особую точку и разложить правые части уравнений по формуле Тейлора, ограничиваясь членами первого порядка:
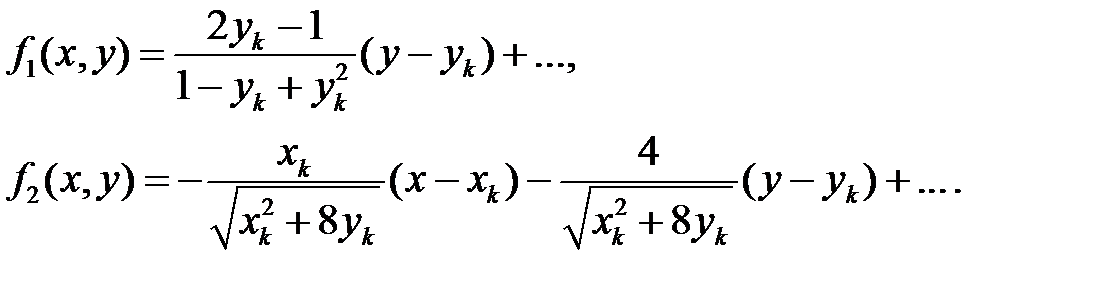
Рассмотрим точку 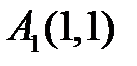 . Наша система примет вид
. Наша система примет вид
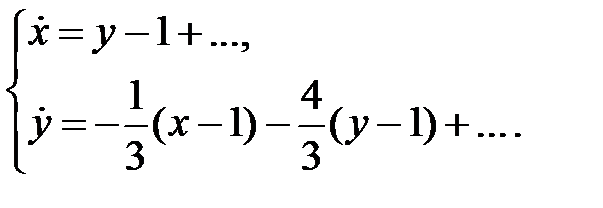
Характеристическое уравнение
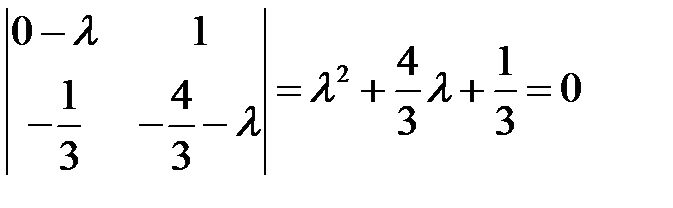 .
.
Оно имеет корни 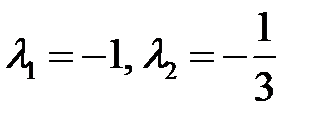 . Следовательно, особая точка
. Следовательно, особая точка 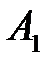 – асимптотически устойчивый узел.
– асимптотически устойчивый узел.
В точке 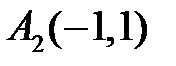 имеем систему
имеем систему
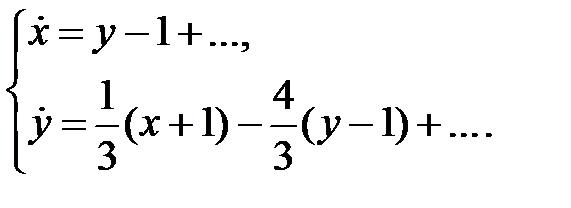
Характеристическое уравнение имеет корни 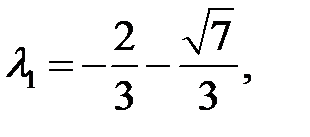
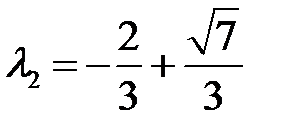 . Отсюда следует, что особая точка
. Отсюда следует, что особая точка 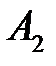 – седло.
– седло.
В точке 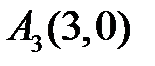 для системы
для системы
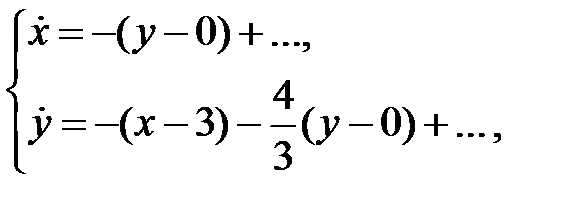
характеристическое уравнение имеет корни 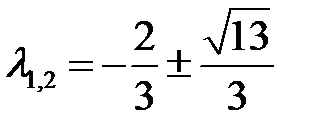 . Следовательно, особая точка
. Следовательно, особая точка 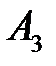 – седло.
– седло.
Аналогично получим для точки 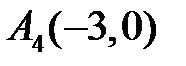 систему
систему
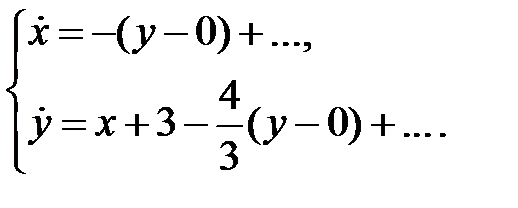
Характеристическое уравнение 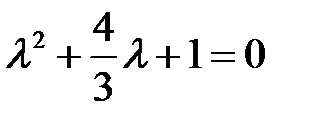 имеет корни
имеет корни 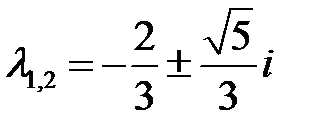 . Поэтому особая точка
. Поэтому особая точка 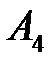 – асимптотически устойчивый фокус.
– асимптотически устойчивый фокус.
6.5. Функции Ляпунова
Рассмотрим функцию 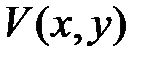 , непрерывно дифференцируемую в некоторой области
, непрерывно дифференцируемую в некоторой области 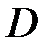 , включающей в себя начало координат.
, включающей в себя начало координат.
Функция 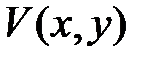 называется определенно положительной в
называется определенно положительной в 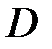 , если
, если 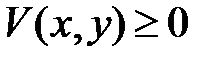 в
в 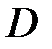 , причем
, причем 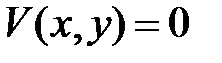 лишь при
лишь при 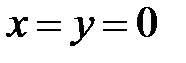 .
.
Функция 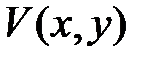 называется определенно отрицательной в
называется определенно отрицательной в 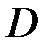 , если
, если 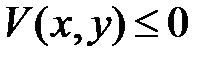 в
в 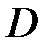 , причем
, причем 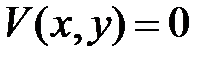 лишь при
лишь при 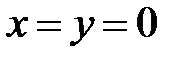 .
.
Функция 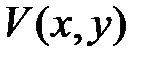 называется знакопостоянной, если
называется знакопостоянной, если 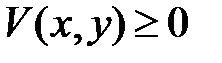 или
или 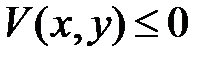 при
при 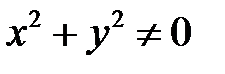 , (причем, в первом случае функция
, (причем, в первом случае функция 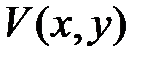 может также названа знакоположительной, а во втором – знакоотрицательной).
может также названа знакоположительной, а во втором – знакоотрицательной).
Пример 22. Функция 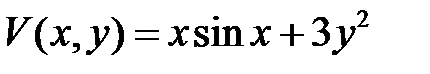 определенно положительна в области
определенно положительна в области 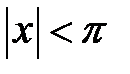 .
.
Пример 23. Функция 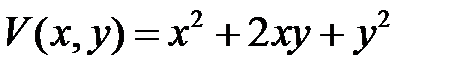 знакоположительна, т.к.
знакоположительна, т.к. 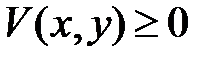 и обращается в нуль при
и обращается в нуль при 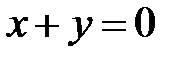 .
.
Пример 24. Функция 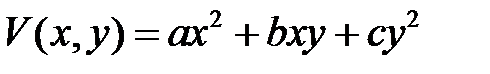 будет определенно положительной, если
будет определенно положительной, если 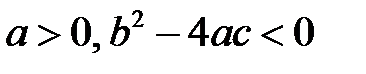 .
.
Рассмотрим систему дифференциальных уравнений
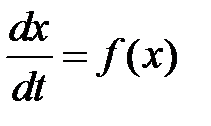 , (11)
, (11)
где вектор-функция 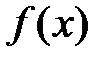 непрерывна и удовлетворяет условию Липшица в области
непрерывна и удовлетворяет условию Липшица в области 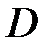 , содержащей точку
, содержащей точку 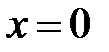 вместе с ее некоторой окрестностью, и
вместе с ее некоторой окрестностью, и 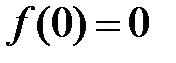 .
.
Теорема 7 (теорема Ляпунова об устойчивости). Если для системы (11) в области 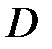 существует знакоопределенная функция
существует знакоопределенная функция 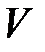 , производная которой
, производная которой 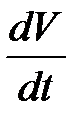 , взятая в силу системы (11), является знакопостоянной функцией, знака, противоположного знака функции
, взятая в силу системы (11), является знакопостоянной функцией, знака, противоположного знака функции 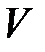 (или
(или 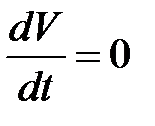 ), то нулевое решение устойчиво.
), то нулевое решение устойчиво.
Теорема 8 (теорема Ляпунова об асимптотической устойчивости). Если для системы в области 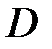 (11) существует знакоопределенная функция V , производная которой
(11) существует знакоопределенная функция V , производная которой 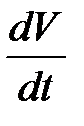 , взятая в силу системы (11), является знакоопределенной функцией, знака, противоположного с
, взятая в силу системы (11), является знакоопределенной функцией, знака, противоположного с 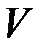 , то нулевое решение асимптотически устойчиво.
, то нулевое решение асимптотически устойчиво.
Теорема 9 (теорема Ляпунова о неустойчивости). Если существует функция 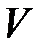 , имеющая знакоопределенную производную
, имеющая знакоопределенную производную 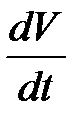 , и такая, что функция
, и такая, что функция 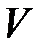 не является знакопостоянной, знака, противоположного знаку
не является знакопостоянной, знака, противоположного знаку 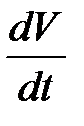 , то нулевое решение системы (11)
, то нулевое решение системы (11) 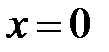 неустойчиво.
неустойчиво.
Теорема 10 (теорема Ляпунова о неустойчивости). Если существует функция 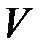 такая, что ее производная по времени имеет вид
такая, что ее производная по времени имеет вид
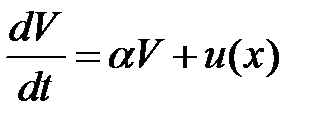 ,
,
где 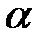 – положительная постоянная, а
– положительная постоянная, а 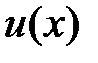 является знакопостоянной функцией, при этом
является знакопостоянной функцией, при этом 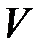 может принимать значения того же знака, что и
может принимать значения того же знака, что и 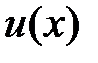 в точках
в точках 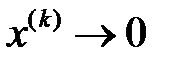 при
при 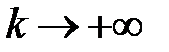 , то нулевое решение системы (11)
, то нулевое решение системы (11) 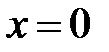 неустойчиво.
неустойчиво.
Из работы А. М. Ляпунова следует, что для системы
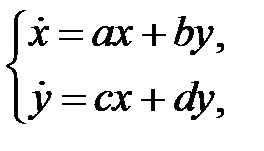 (12)
(12)
когда характеристическое уравнение имеет корни 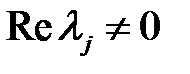 , существует функция
, существует функция
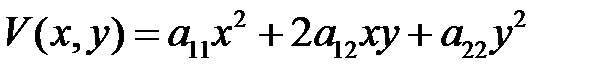 , (13)
, (13)
имеющая знакоопределенную производную 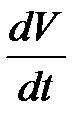 .
.
Пример 25. Исследовать на устойчивость нулевое решение системы
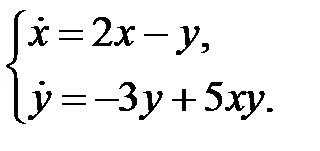
Решение. Характеристическое уравнение 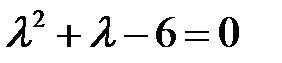 имеет корни
имеет корни 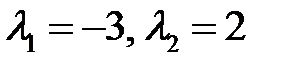 , следовательно,
, следовательно, 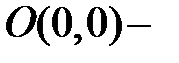 седло. Возьмем функцию
седло. Возьмем функцию 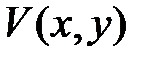 вида (13) и найдем
вида (13) и найдем
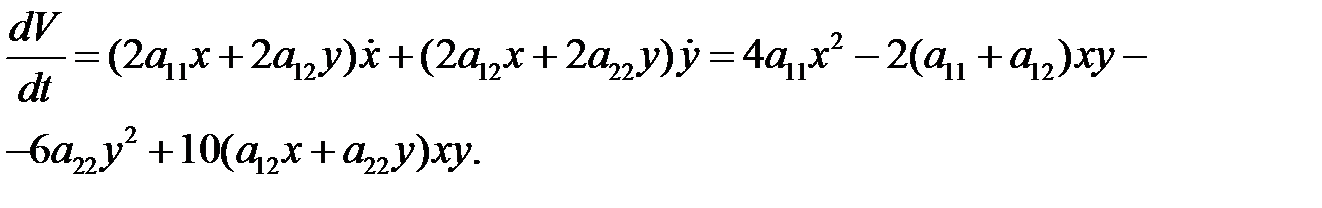
Если выбрать 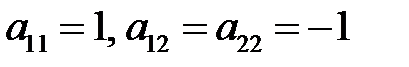 , то функция
, то функция 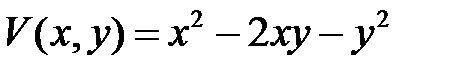 имеет производную
имеет производную 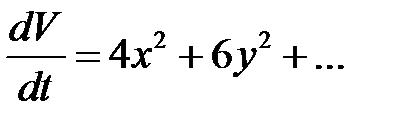 . Из теоремы 9 следует, что нулевое решение данной системы неустойчиво.
. Из теоремы 9 следует, что нулевое решение данной системы неустойчиво.
Пример 26. Исследовать на устойчивость нулевое решение системы
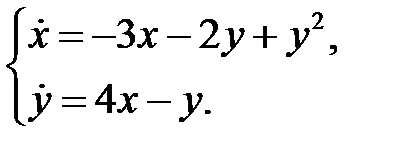
Решение. Характеристическое уравнение 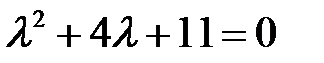 имеет корни
имеет корни 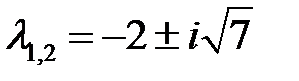 . Для функции
. Для функции 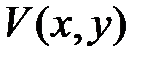 вида (13) производная
вида (13) производная
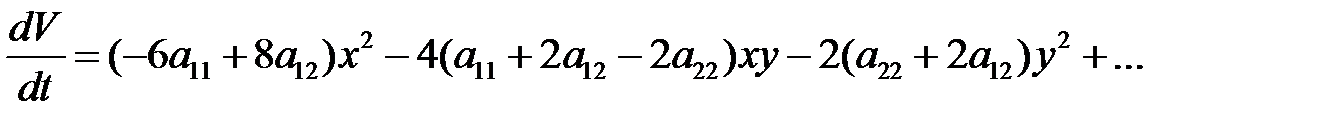 .
.
Если выбрать 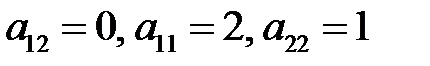 , то функция
, то функция
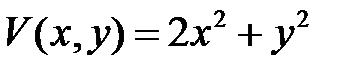
имеет производную
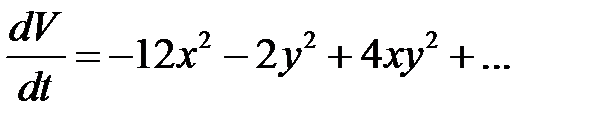 ,
,
которая определенно отрицательна. Следовательно, функция 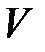 удовлетворяет условиям теоремы 8 и нулевое решение асимптотически устойчиво.
удовлетворяет условиям теоремы 8 и нулевое решение асимптотически устойчиво.
Замечание 1. Общего метода построения функции Ляпунова нет. В простейших случаях функцию Ляпунова можно искать в следующих видах:
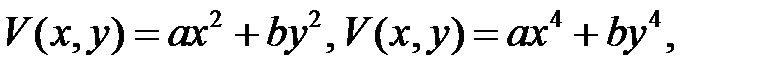
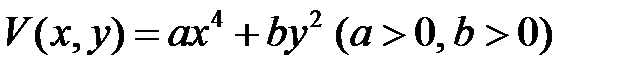 и т.д.
и т.д.
Замечание 2. Теорема 8 может быть применена, если характеристическое уравнение системы (12) имеет корни 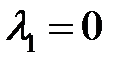 и
и 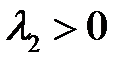 .
.
Пример 27. Построить функцию Ляпунова для системы
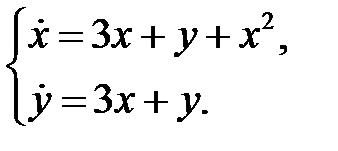
Решение. Характеристическое уравнение 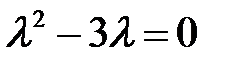 имеет корни
имеет корни 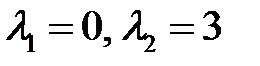 . Будем искать функцию
. Будем искать функцию 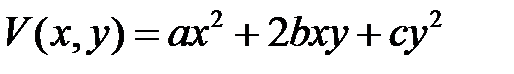 , которая имела бы производную
, которая имела бы производную 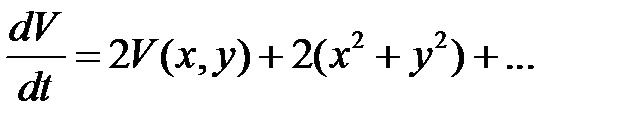 .
.
Сравнивая коэффициенты при 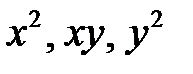 получим систему уравнений
получим систему уравнений
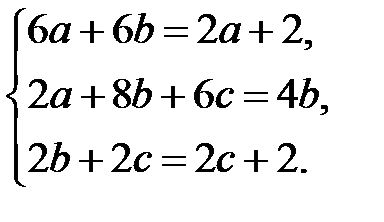
Из этой системы найдем 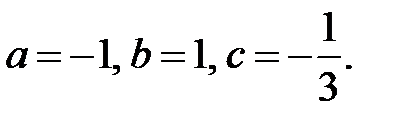 Тогда
Тогда
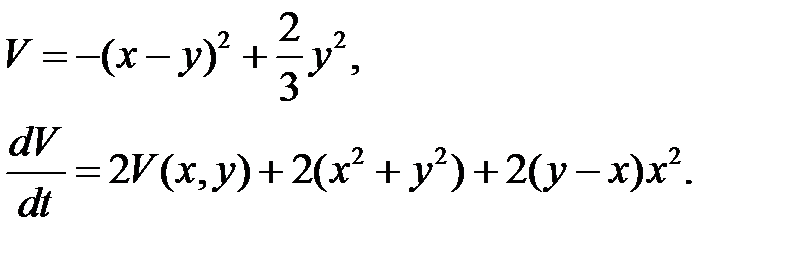
Здесь функция 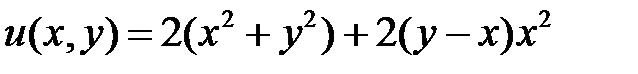 знакоположительная и, применяя теорему 10, доказываем, что нулевое решение неустойчиво.
знакоположительная и, применяя теорему 10, доказываем, что нулевое решение неустойчиво.
6.6. Индивидуальные задания








