Линейные системы дифференциальных уравнений

Дата: 2025-06-14; Просмотры: 6
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

6.1. Линейные однородные системы дифференциальных уравнений

с постоянными коэффициентами

Линейная система дифференциальных уравнений имеет вид

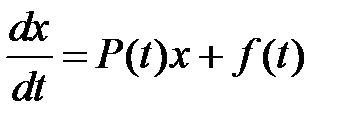, (1)

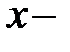
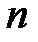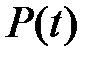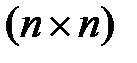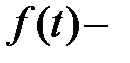
где -мерный вектор, - матрица размерности , 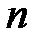-мерная вектор-функция, их элементы заданы и непрерывны на интервале .

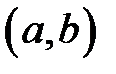Вместе с системой (1) рассмотрим соответствующую однородную систему

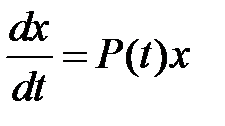. (2)

Фундаментальной системой решений системы (2) называют набор 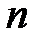линейно независимых решений 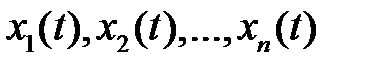, а фундаментальной матрицей – матрицу :

, .

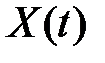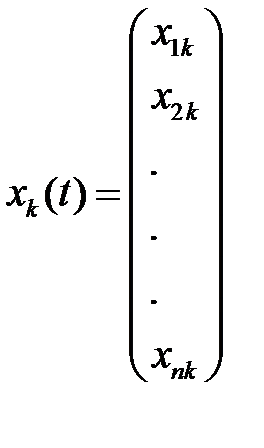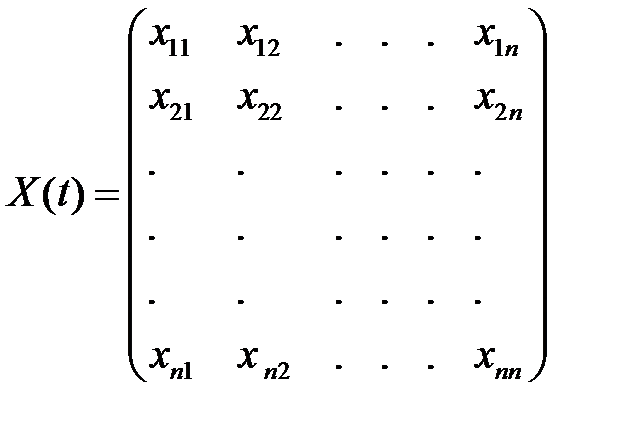Теорема 1. Если 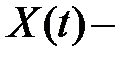фундаментальная матрица системы (2), то для любого её решения 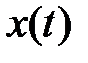найдется единственный вектор-столбец такой, что

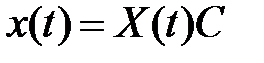. (3)

Отсюда следует, что общее решение системы (2) имеет вид (3).

Пусть матрица 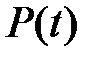постоянная, т.е. 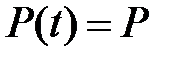. Для построения фундаментальной матрицы линейной однородной системы с постоянными коэффициентами применяются два метода: метод Эйлера и матричный метод. Изложим метод Эйлера.

Найдем собственные числа матрицы 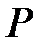, т.е. корни уравнения

.

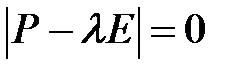Если собственное число 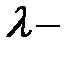вещественное и простое, найдем соответствующий собственный вектор из системы уравнений

.

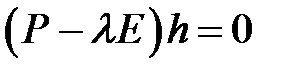Тогда этому корню будет соответствовать решение

.

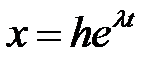Если 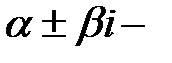пара простых комплексно-сопряженных собственных чисел матрицы 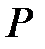, то соответствующий собственный вектор 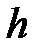будет иметь вид

.

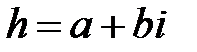Тогда получим два линейно независимых решения

,

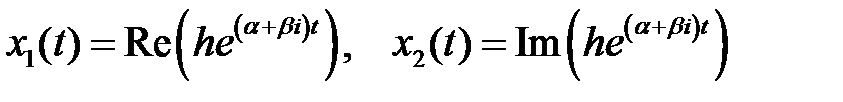т.е. 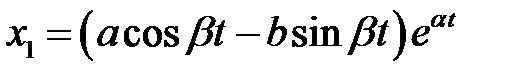и .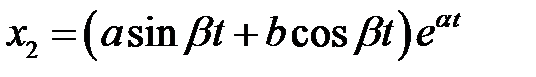

Если 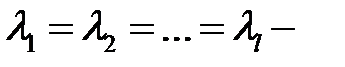кратные корни характеристического уравнения, и 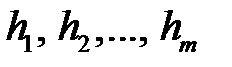находятся из системы уравнений

,

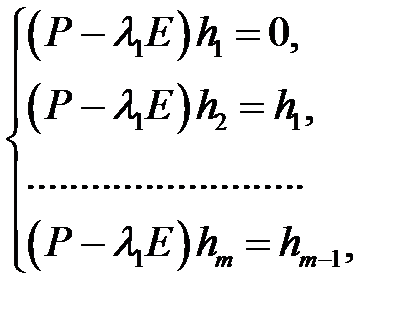
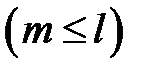то этим кратным корням соответствуют решения

.

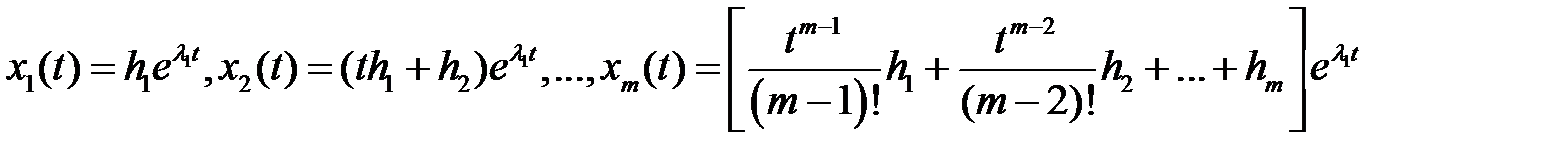Пример 1. Найти общее решение системы

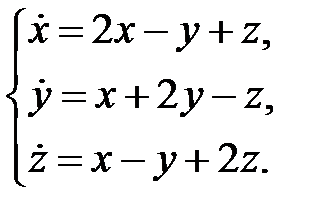
Решение. Составляем характеристическое уравнение

,

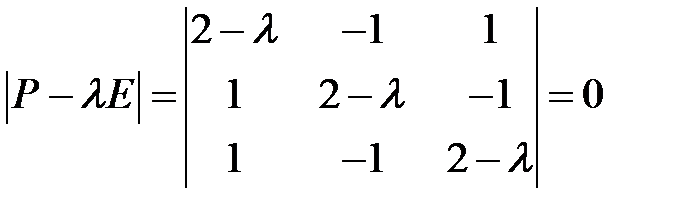которое имеет корни 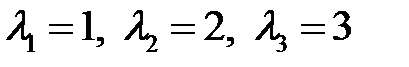. Для определения собственного вектора, соответствующего 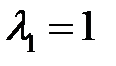, получаем систему уравнений

,

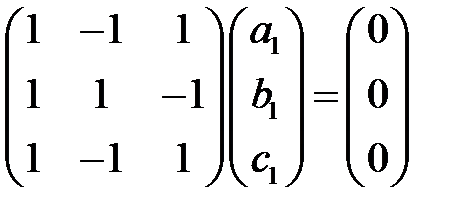которая сводится к двум уравнениям

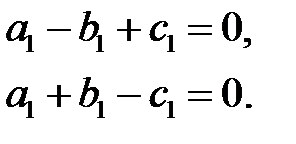
Полагая, что 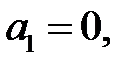находим 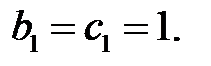Поэтому собственному числу 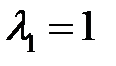соответствует решение

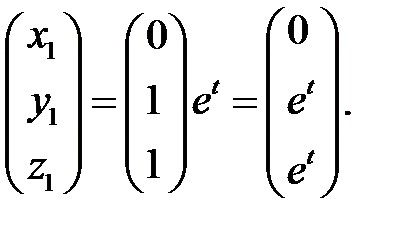
Аналогично находим два решения, соответствующие корням :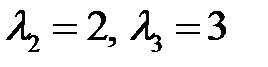

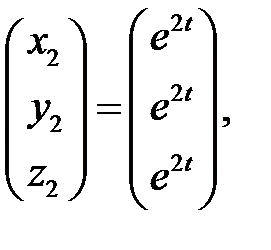
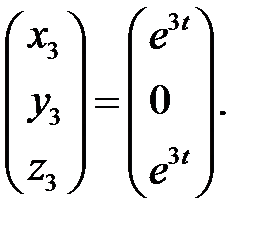
Общее решение будет иметь вид:

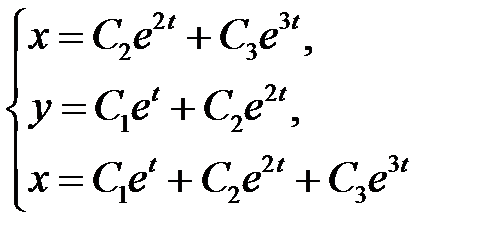или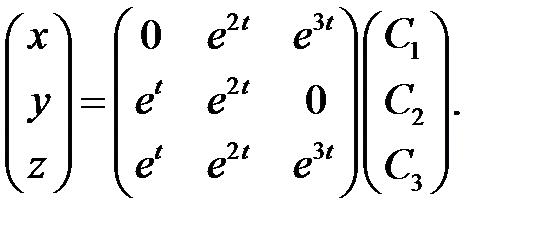

Пример 2. Найти общее решение системы

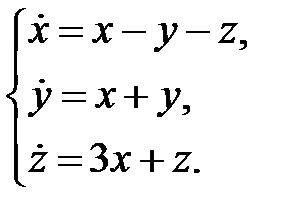
Решение. Характеристическое уравнение

,

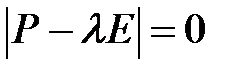имеет корни 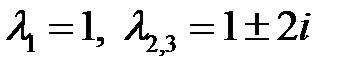. Для корня 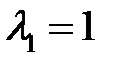имеем

.

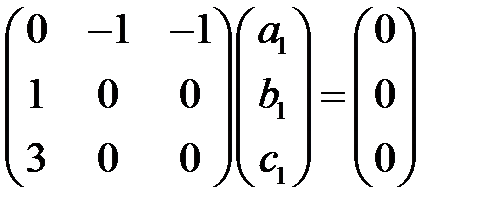Отсюда находим собственный вектор и соответствующее ему решение

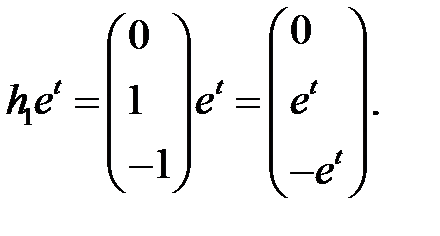
Для корня 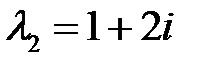находим собственный вектор из системы

.

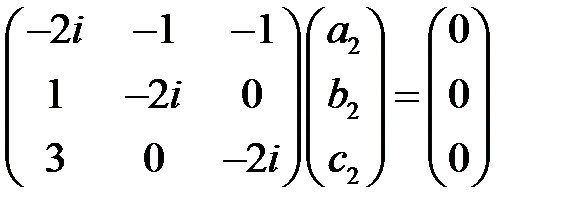Отсюда

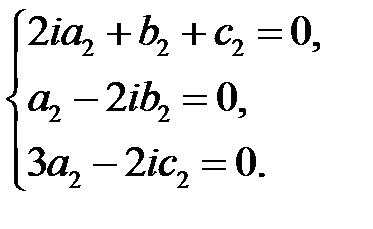
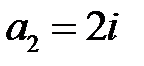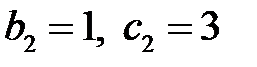Если , то . Соответствующее комплексное решение имеет вид

.

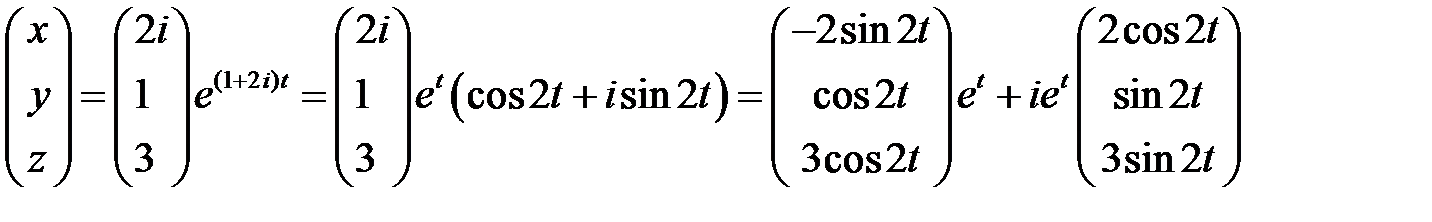Поэтому имеем два вещественных решения

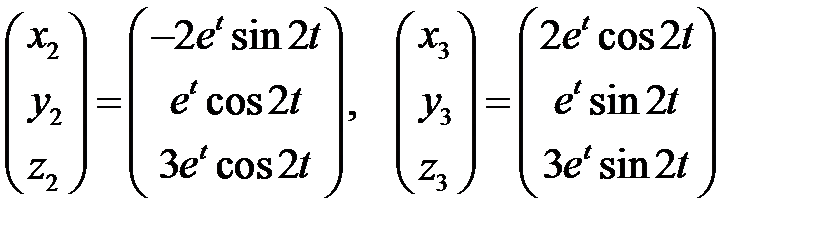и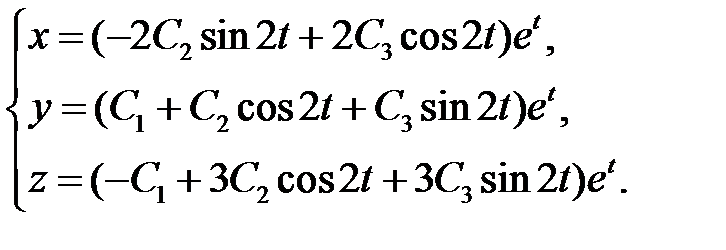

Пример 3. Найти общее решение системы

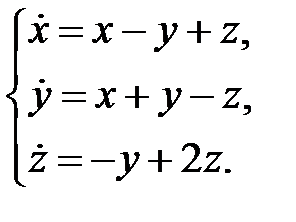
Решение. Характеристическое уравнение

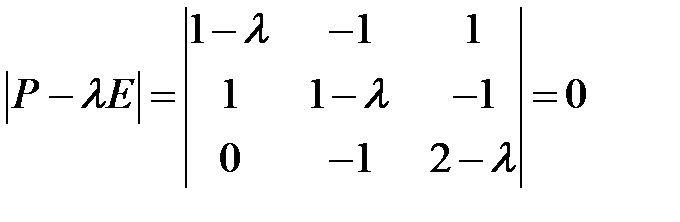
имеет корни 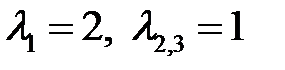. Для корня 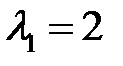найдем решение вида

.

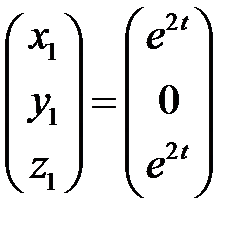Для корня 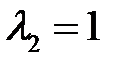найдем собственный вектор

.

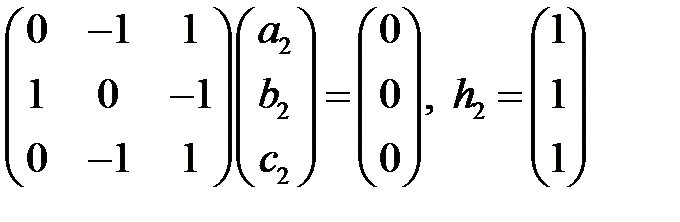Вторым решением, таким образом, является

.

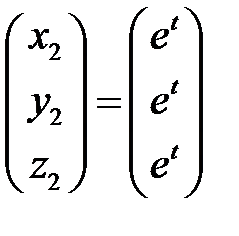Так как ранг матрицы 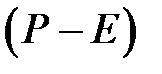равен 2, то для определения присоединенного вектора имеем систему уравнений

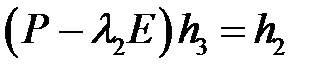или .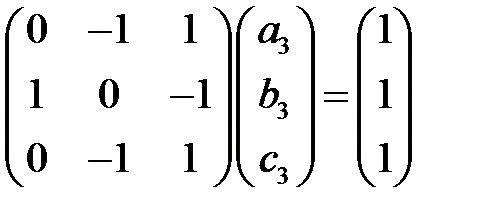

Решая систему

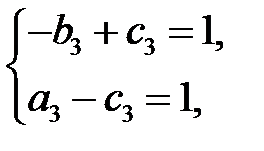
находим 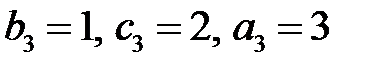. Тогда третьим решением будет

.
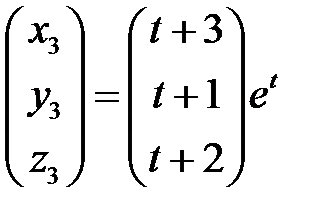