Задание № 20. Линейные уравнения с переменными коэффициентами
 Найти общие решения уравнений, находя их частные решения методом подбора, например, в виде показательной функции
Найти общие решения уравнений, находя их частные решения методом подбора, например, в виде показательной функции 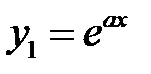 или алгебраического многочлена
или алгебраического многочлена 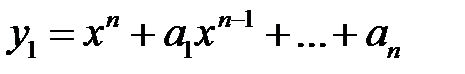 .
.
 Найти решение задачи Коши.
Найти решение задачи Коши.
 Найти решение уравнения в виде степенного ряда, удовлетворяющего начальным условиям.
Найти решение уравнения в виде степенного ряда, удовлетворяющего начальным условиям.
 Решить уравнение Бесселя.
Решить уравнение Бесселя.
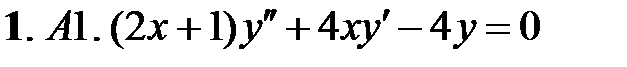 ;
; 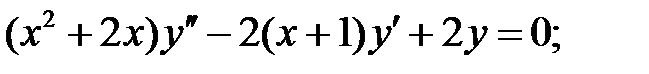
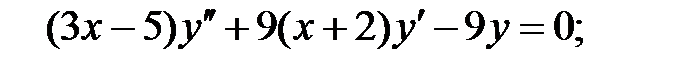
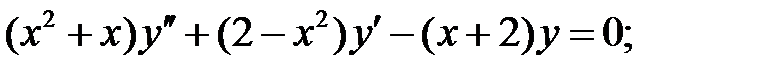
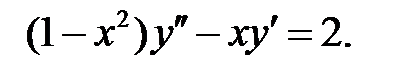
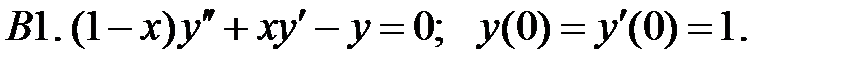
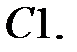
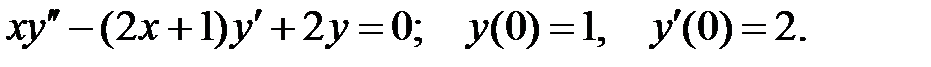
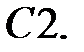
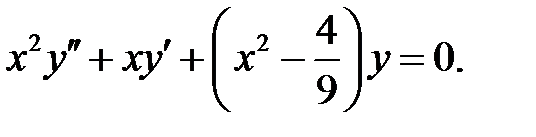
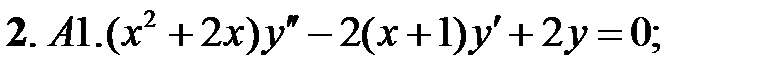
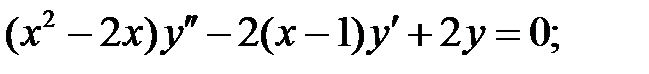
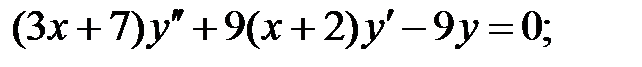
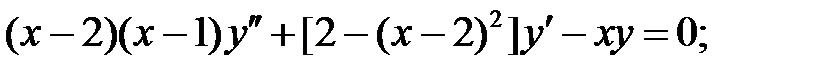
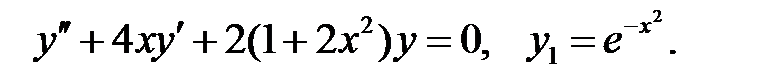
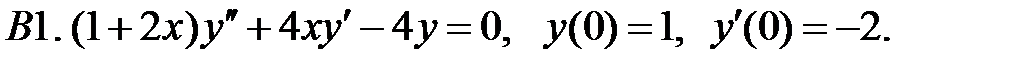
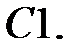
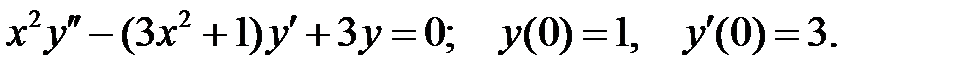
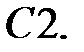
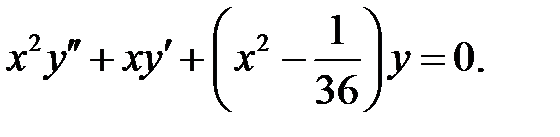
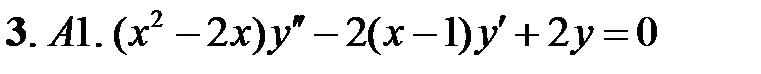 ;
; 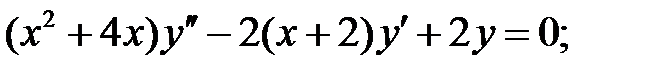
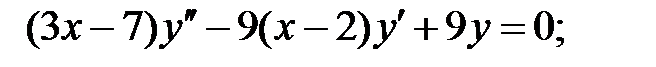
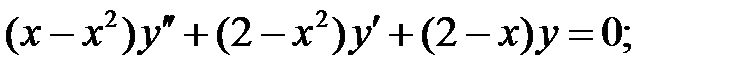
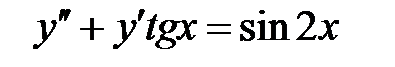
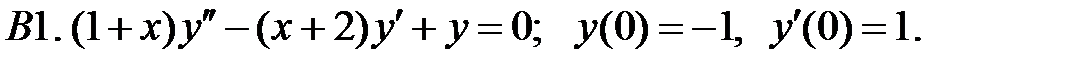
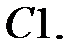
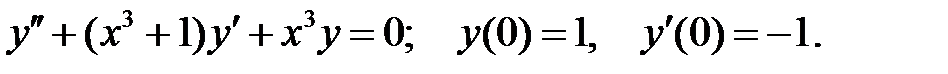
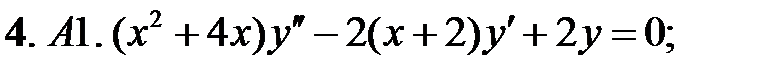
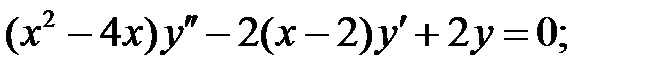
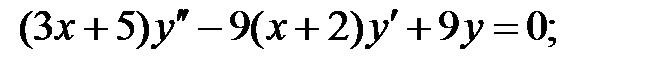
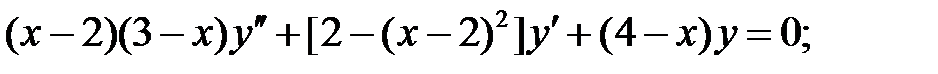
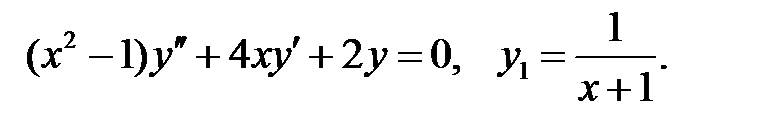
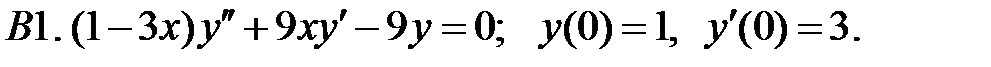
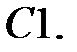
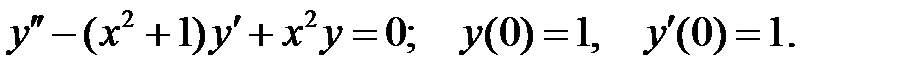
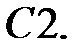
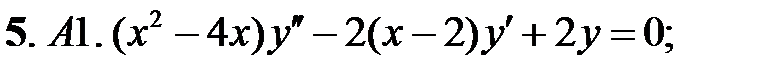
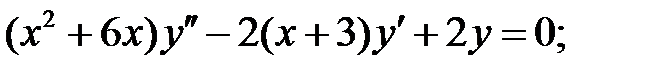
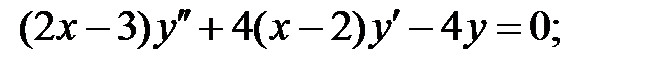
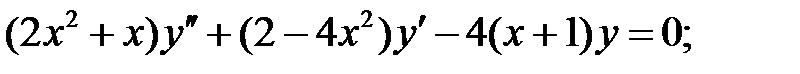
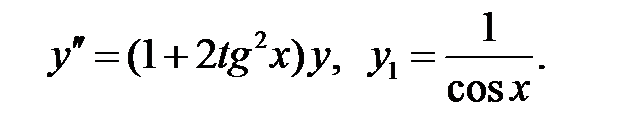
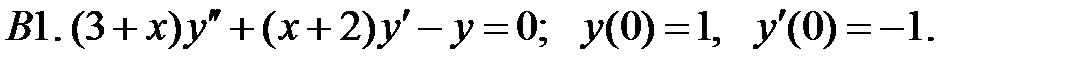
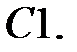
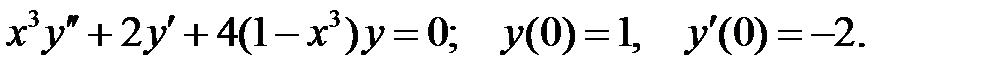
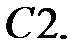
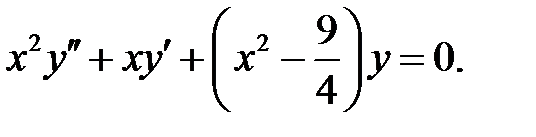
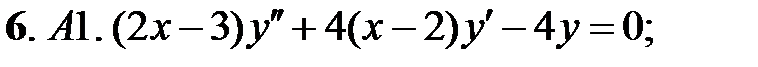
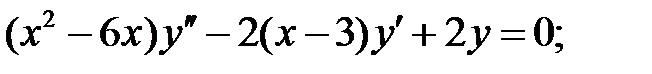
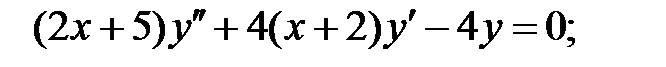
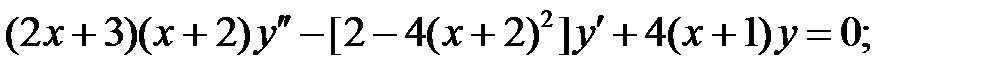
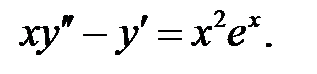
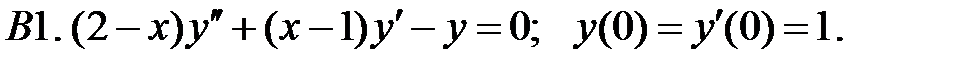
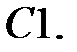
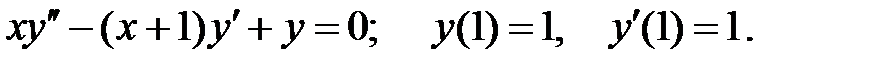
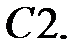
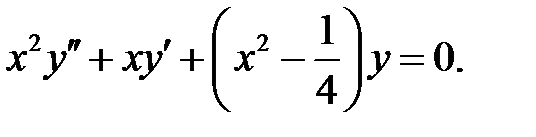
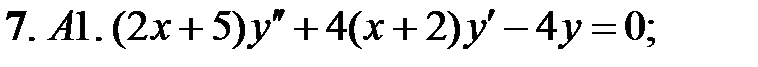
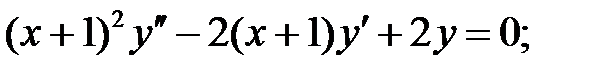
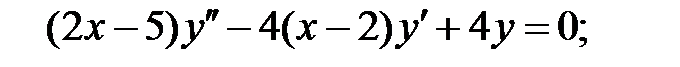
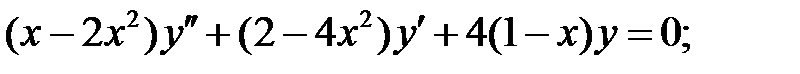
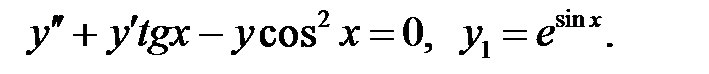
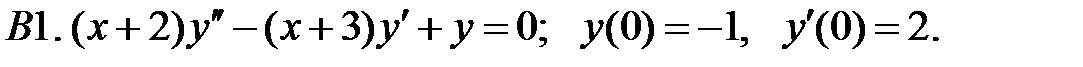
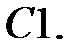
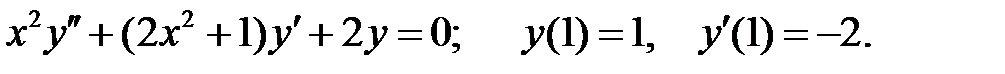
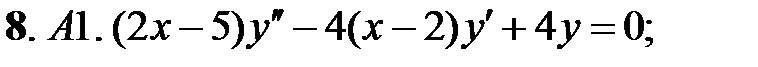
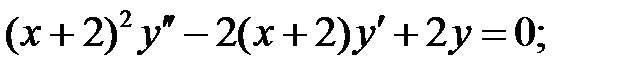
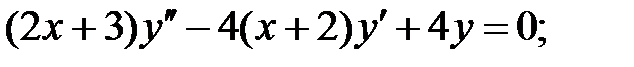
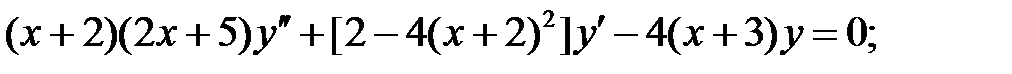
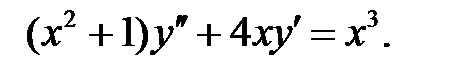
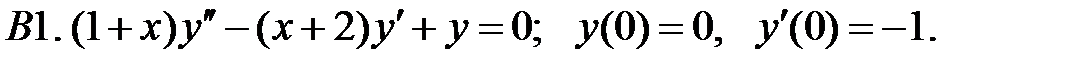
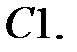
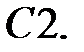
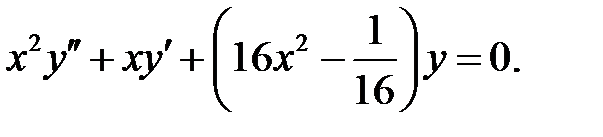
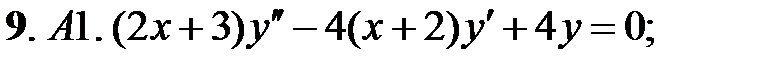
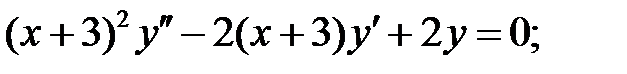
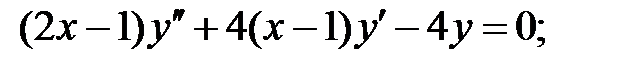
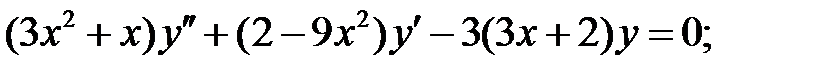
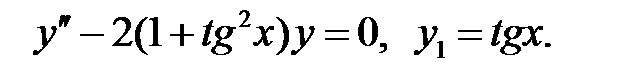
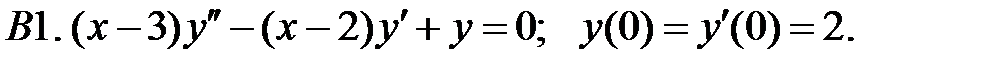
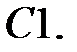
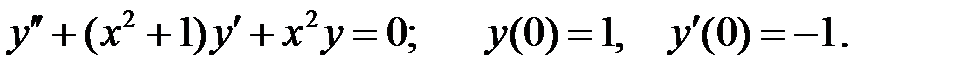
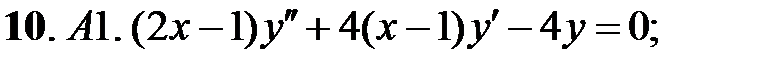
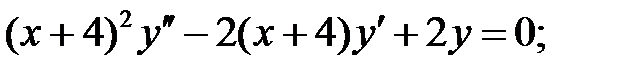
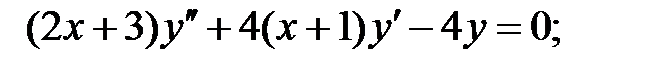
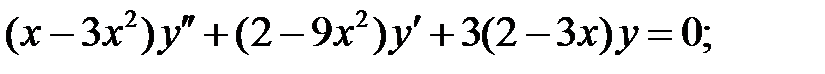
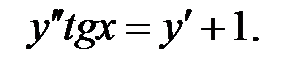
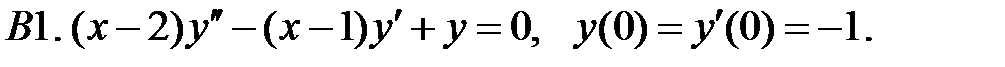
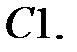
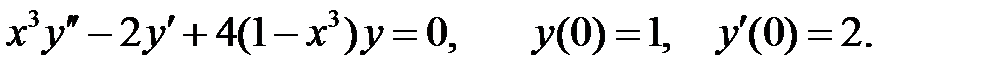
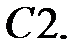
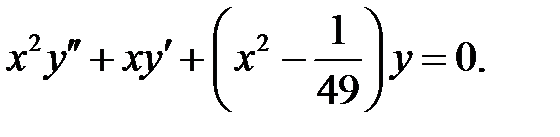
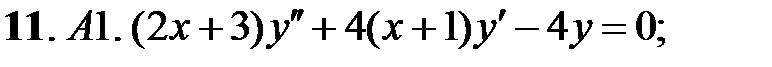
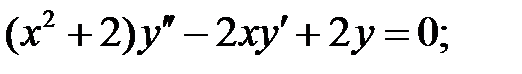
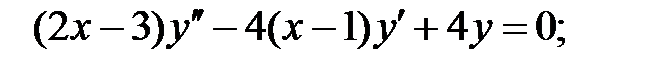
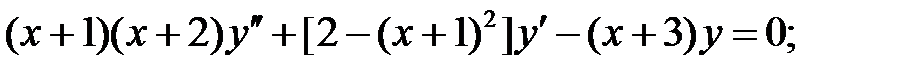
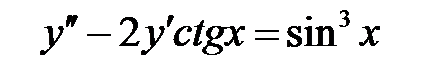 .
.
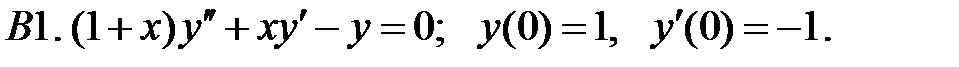
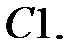
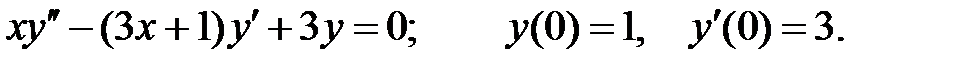
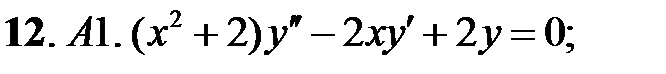
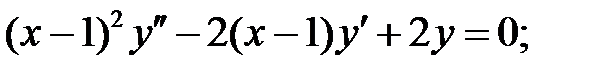
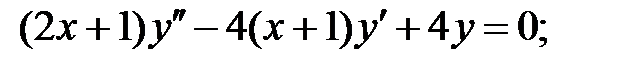
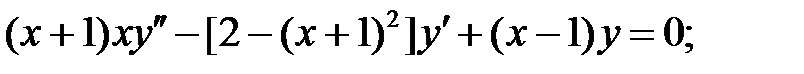
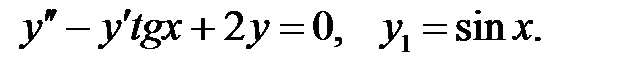
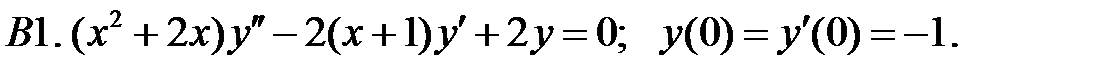
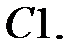
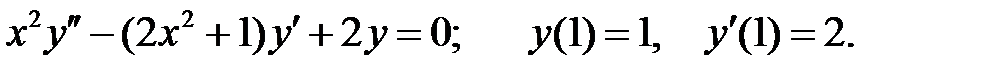
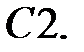
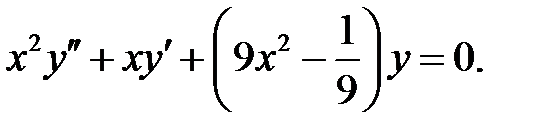
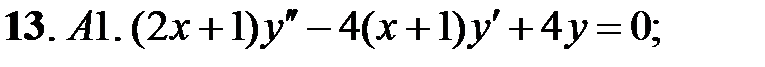
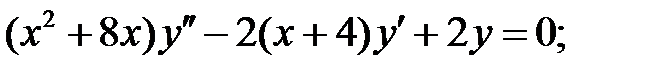
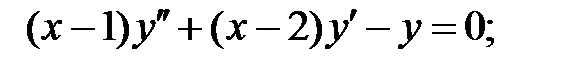
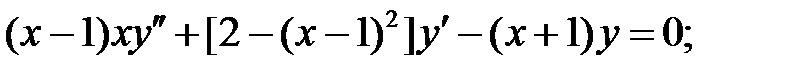
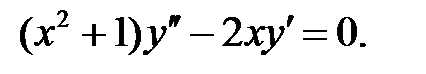
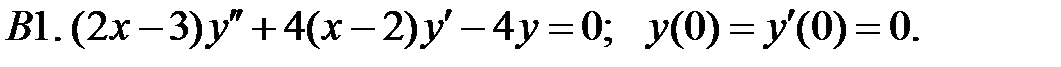
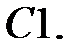
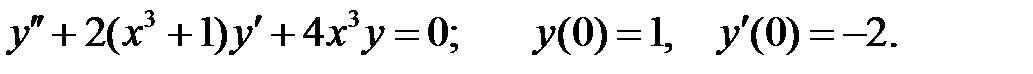
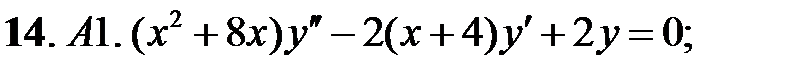
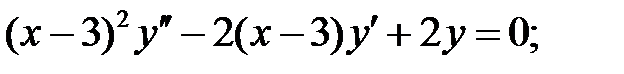
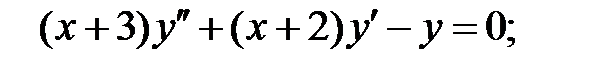
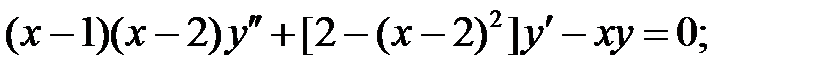
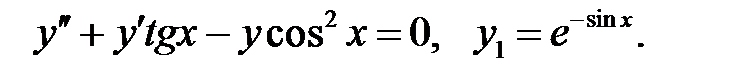
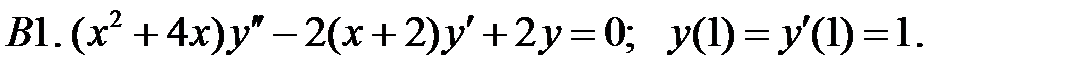
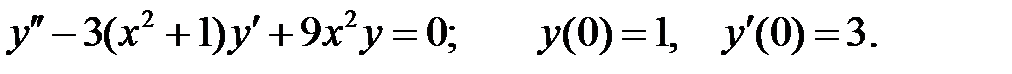
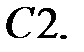
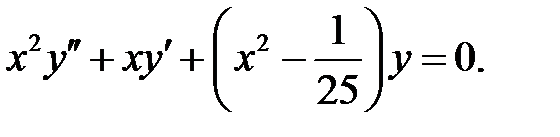
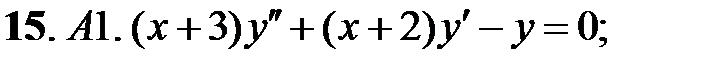
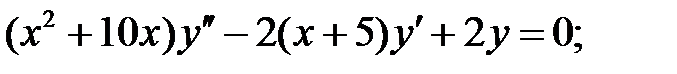
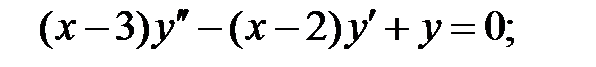
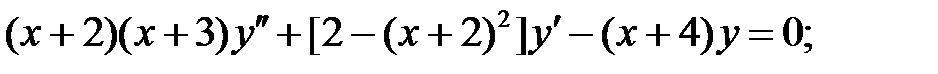
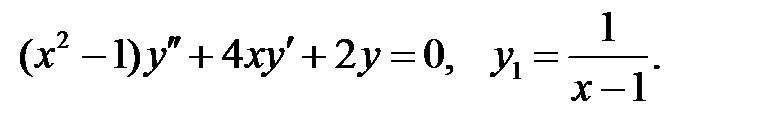
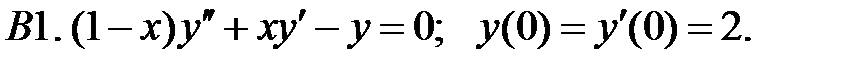
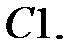
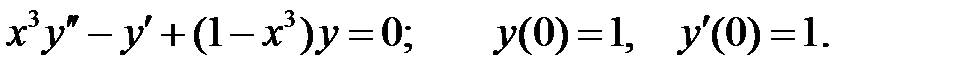
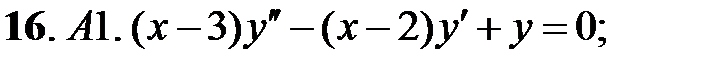
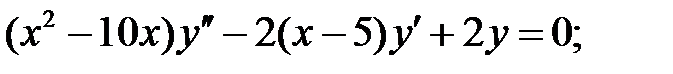
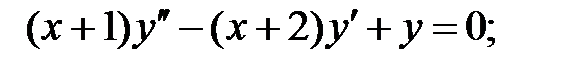
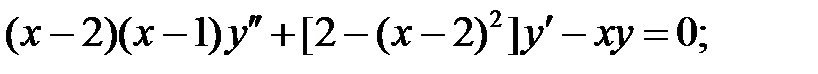
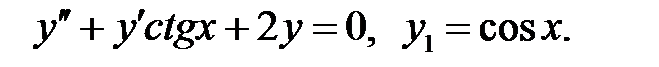
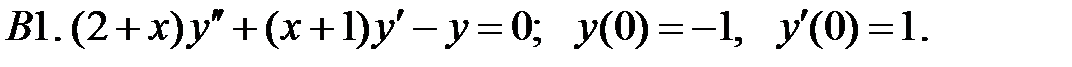
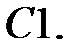
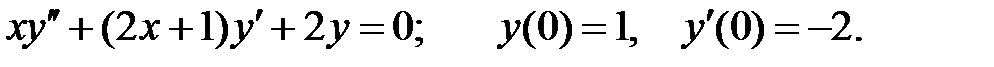
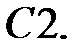
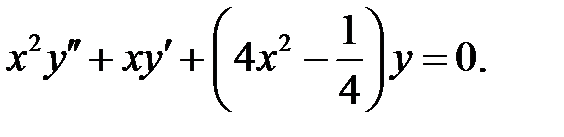
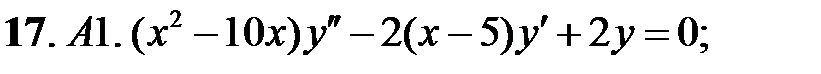
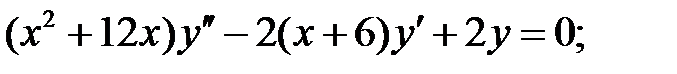
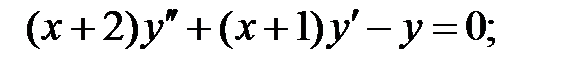
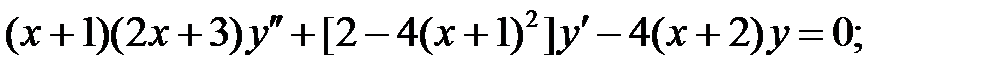
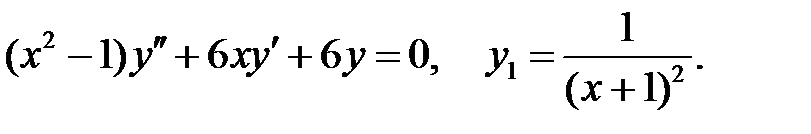
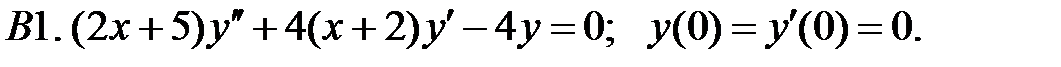
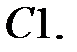
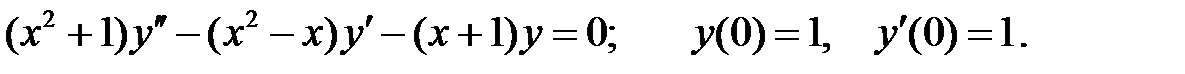
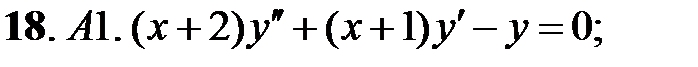
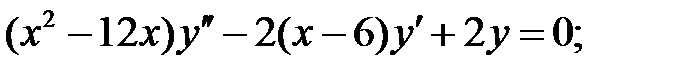
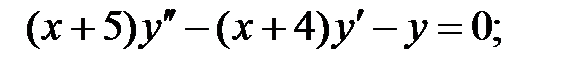
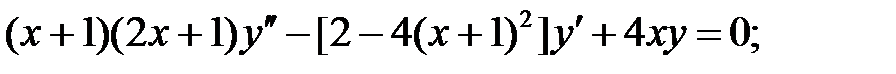
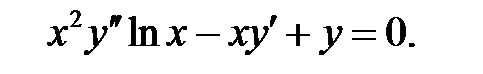
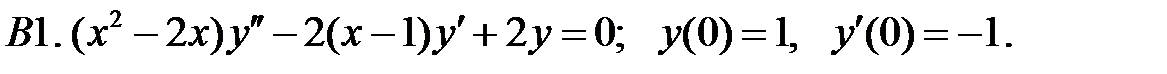
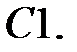
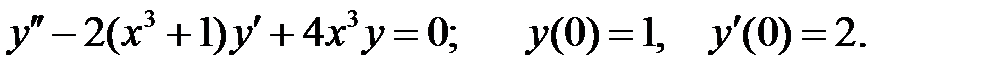
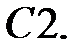
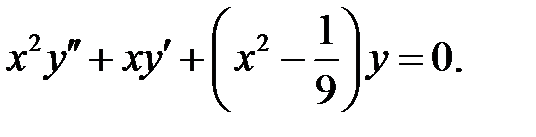
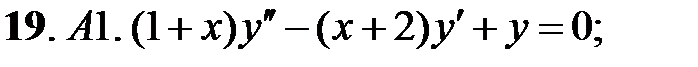
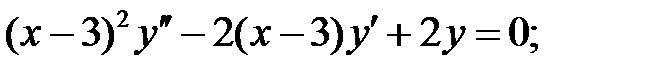
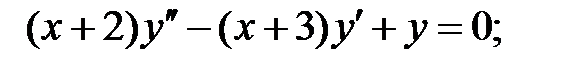
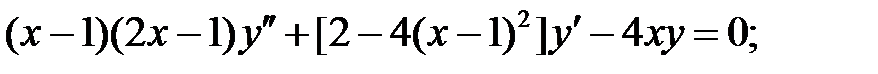
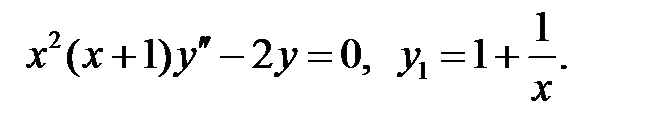
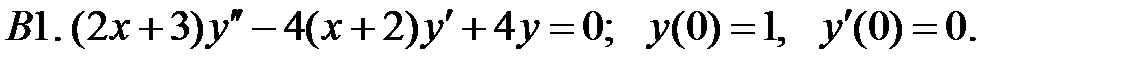
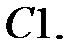
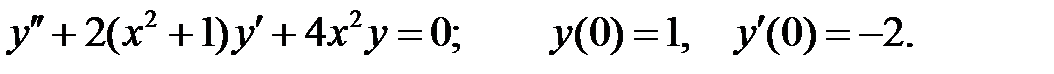
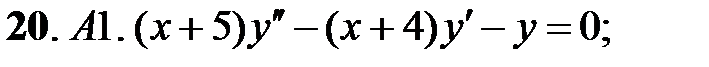
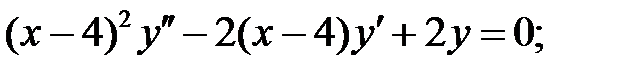
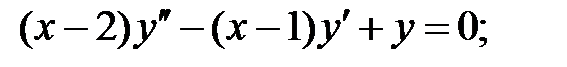
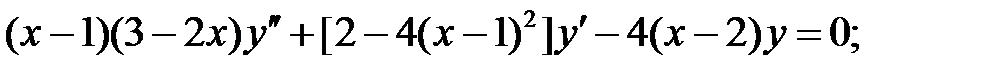
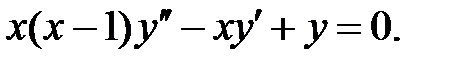
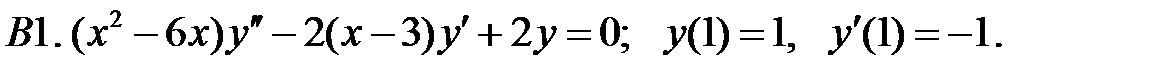
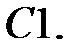
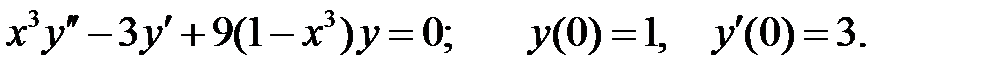
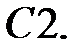
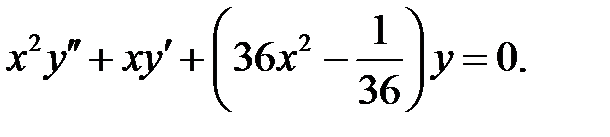
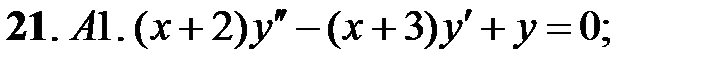
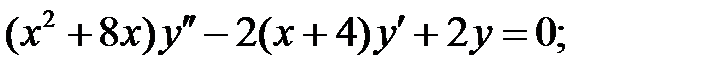
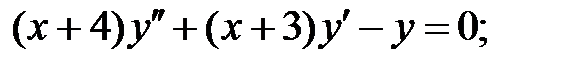
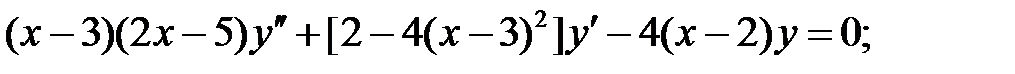
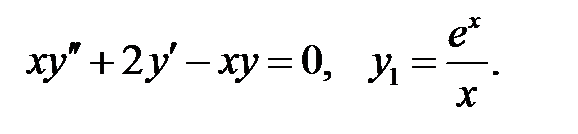
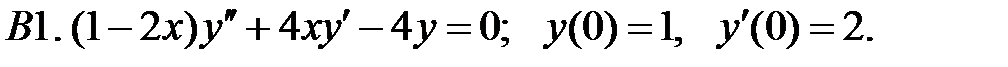
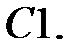
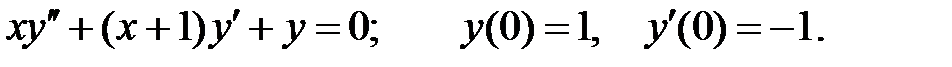
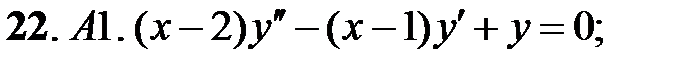
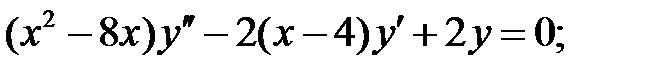
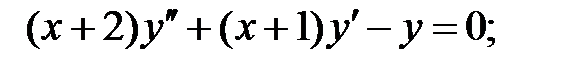
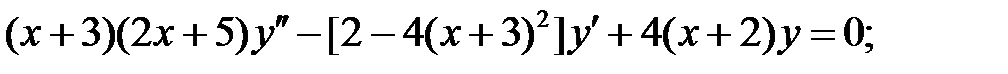
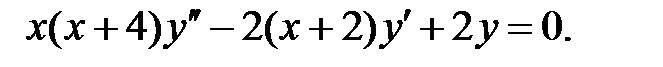
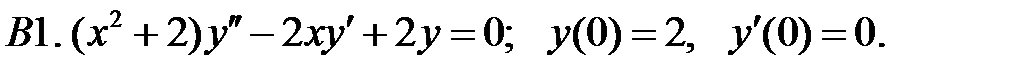
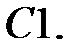
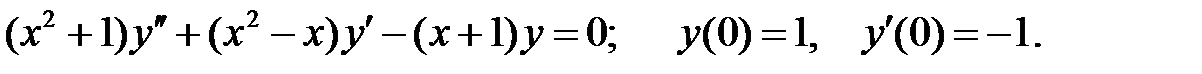
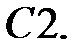
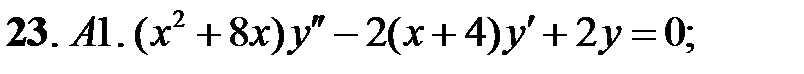
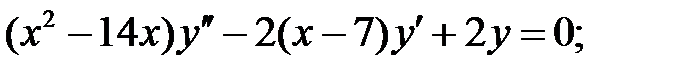
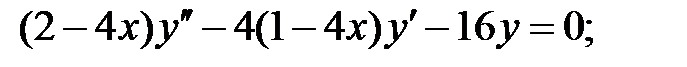
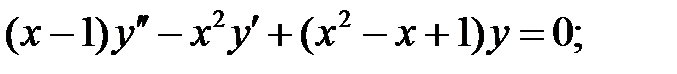
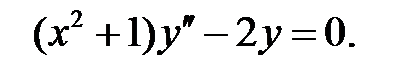
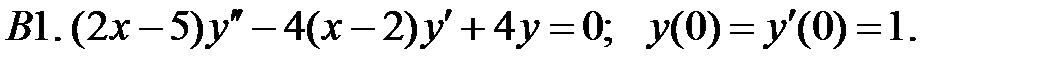
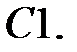
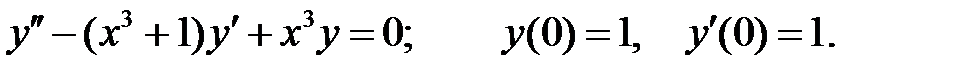
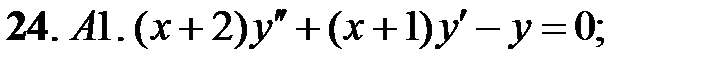
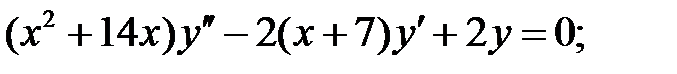
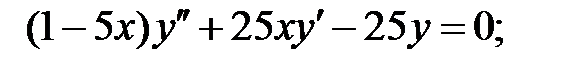
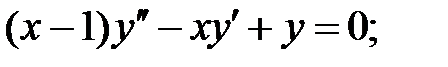
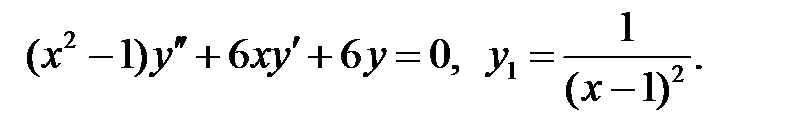
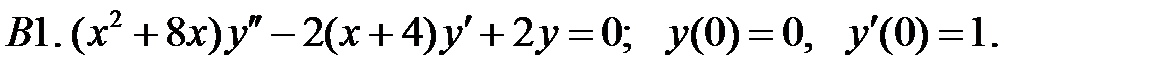
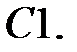
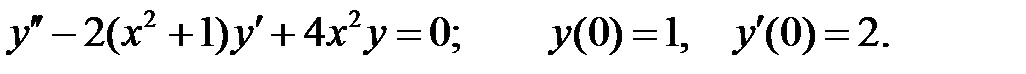
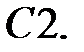
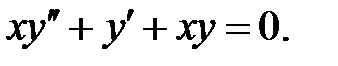
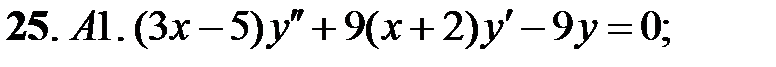
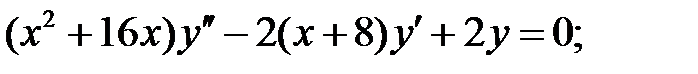
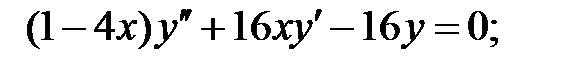
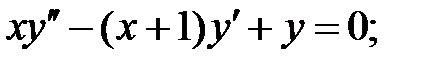
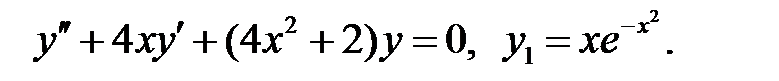
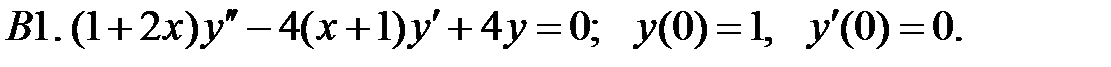
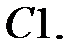
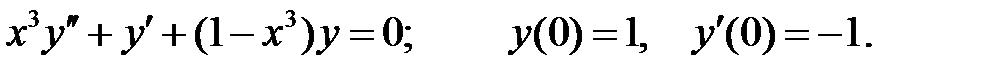
Задание № 21. Уравнения Эйлера
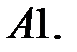 Решить уравнения Эйлера.
Решить уравнения Эйлера.
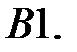 Составить уравнение Эйлера по фундаментальной системе решений (ФСР).
Составить уравнение Эйлера по фундаментальной системе решений (ФСР).
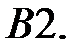 Найти общее решение уравнения.
Найти общее решение уравнения.
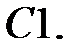 Найти общее решение уравнения.
Найти общее решение уравнения.
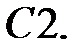 Найти решение уравнения, удовлетворяющее указанным условиям.
Найти решение уравнения, удовлетворяющее указанным условиям.
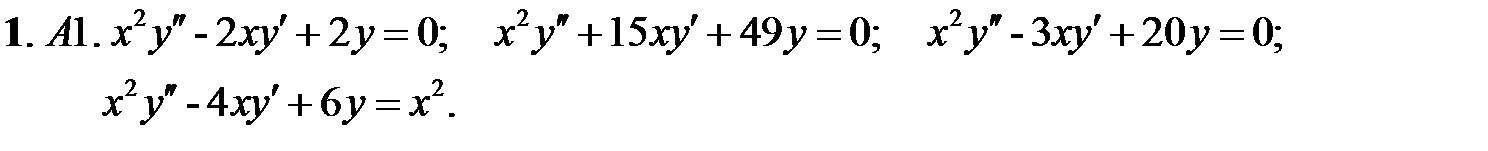
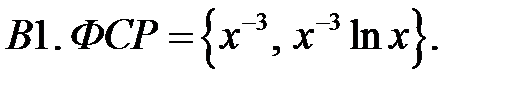
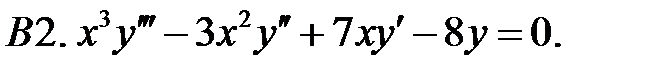
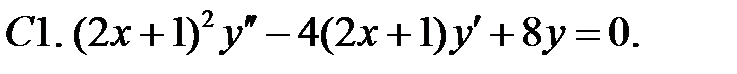
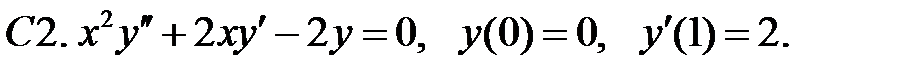
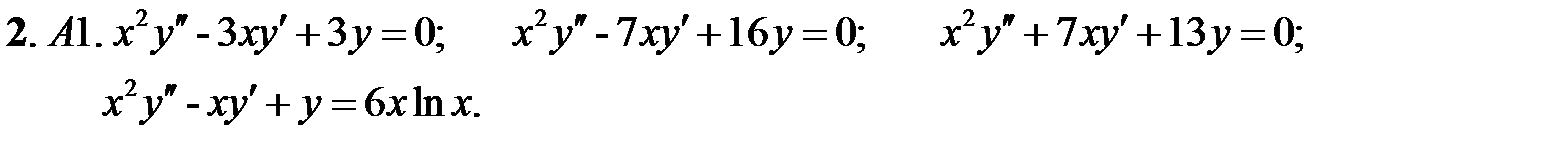
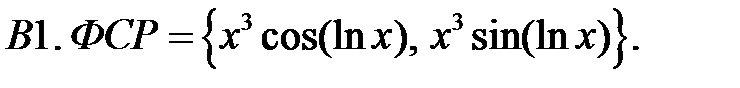
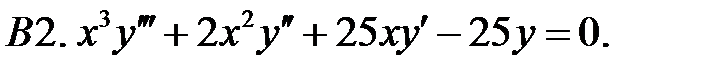
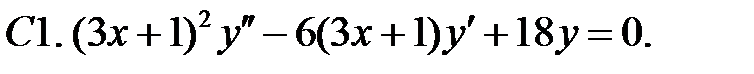
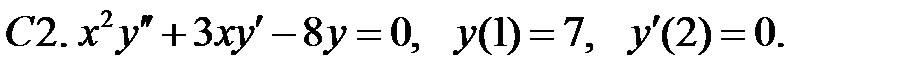
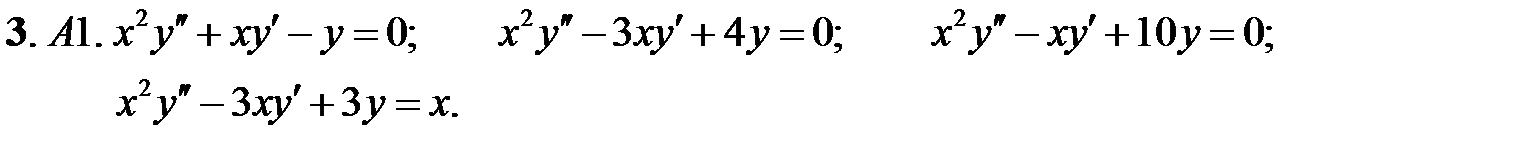
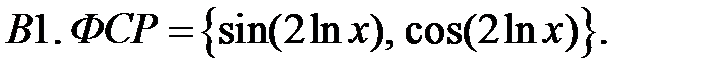
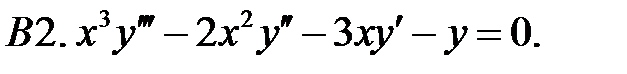
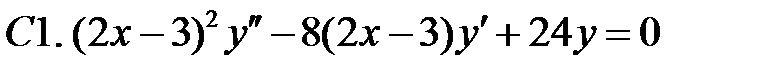
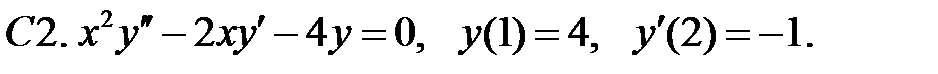
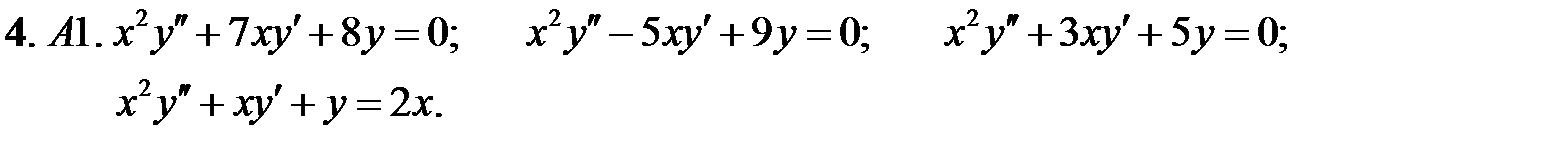
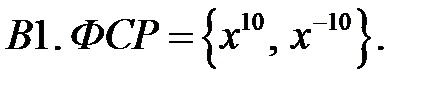
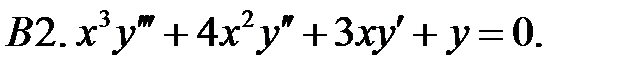
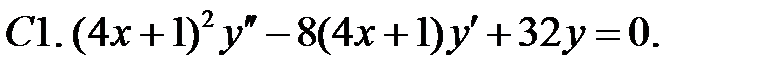
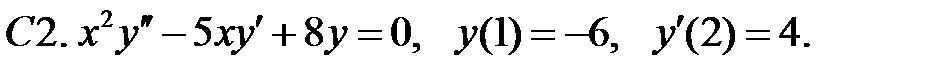
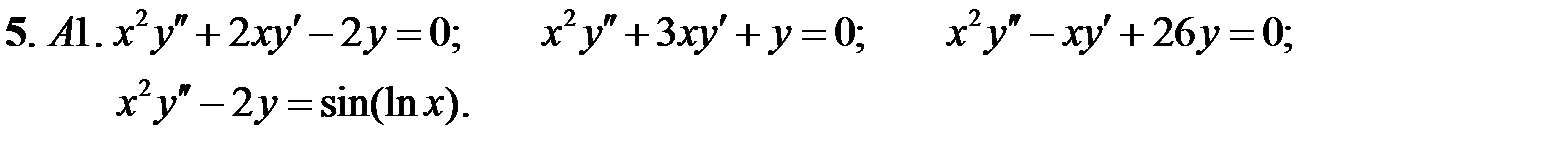
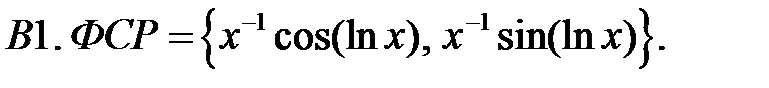
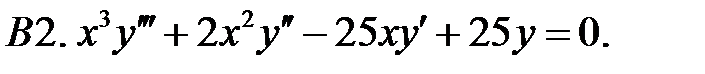
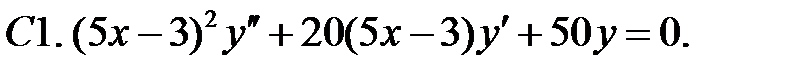
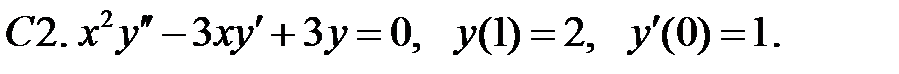
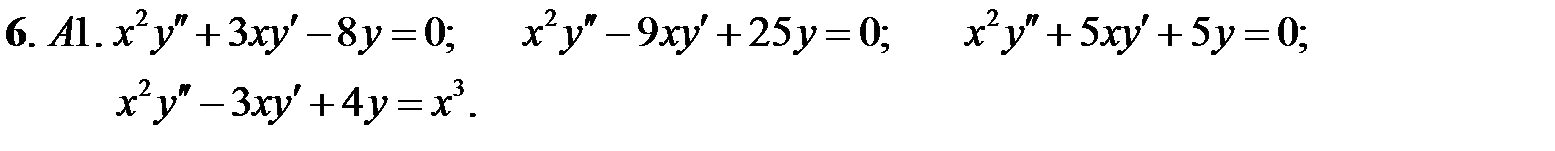
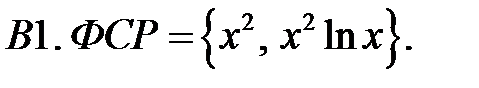
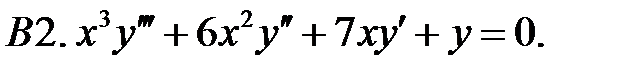
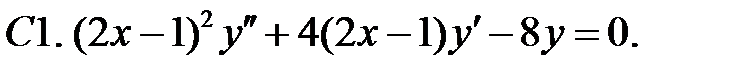
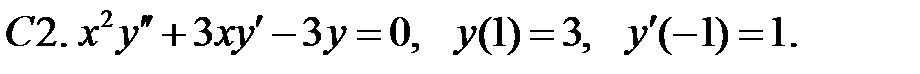
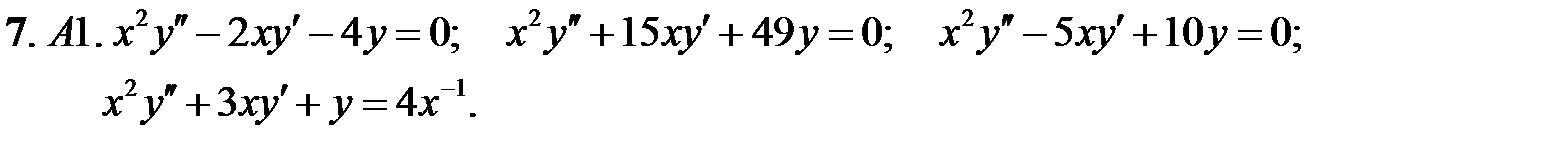
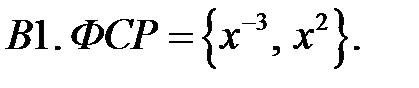
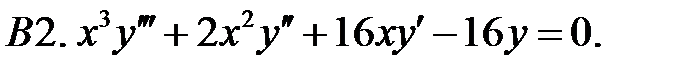
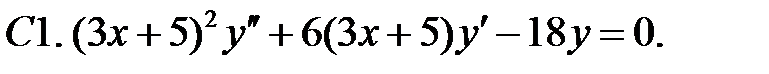
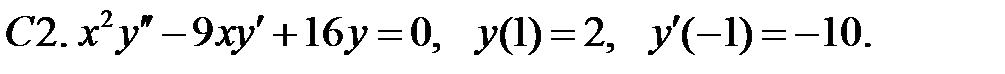
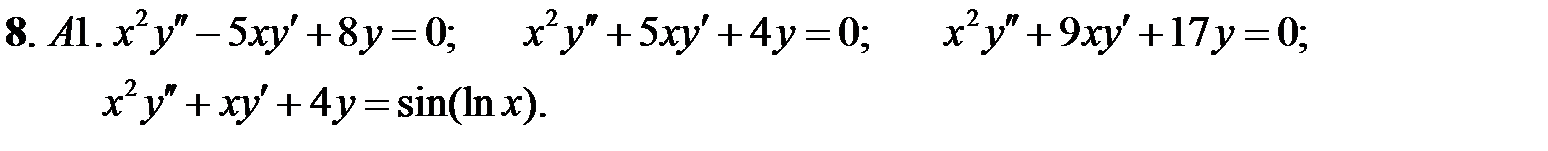
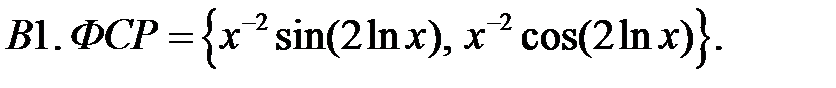
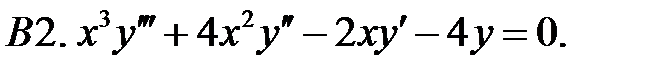
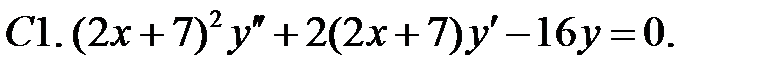
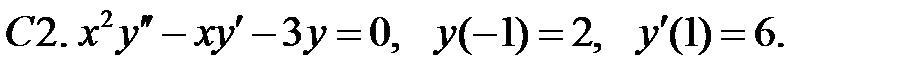
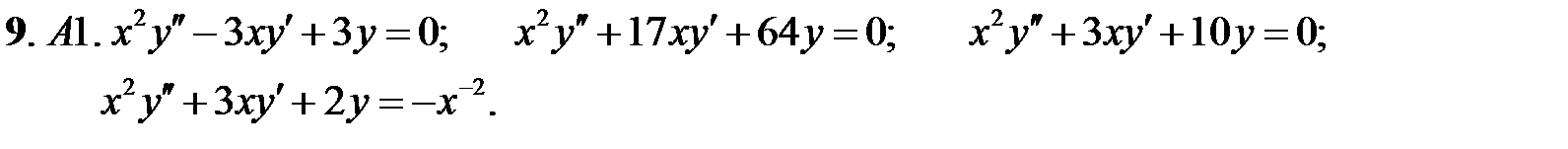
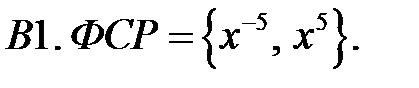
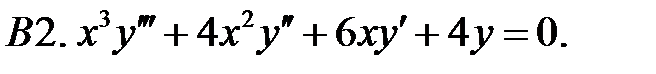
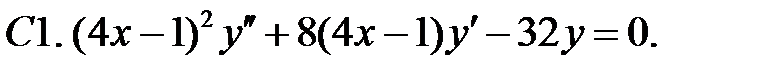
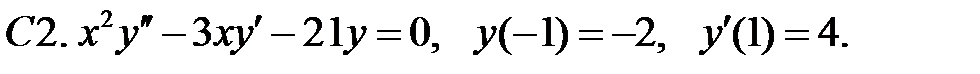
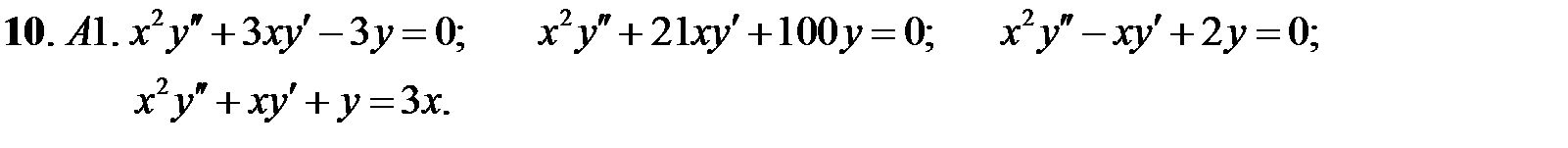
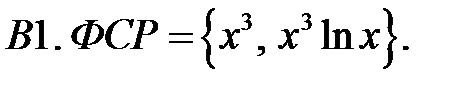
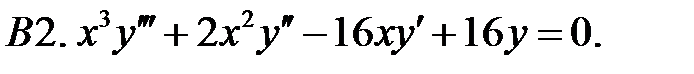
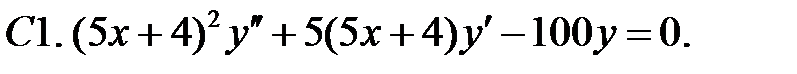
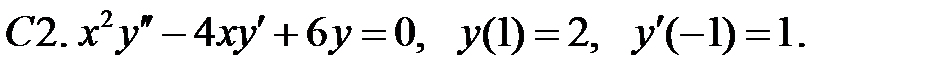
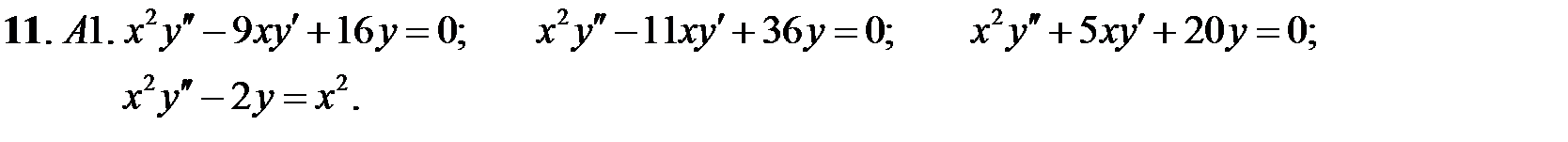
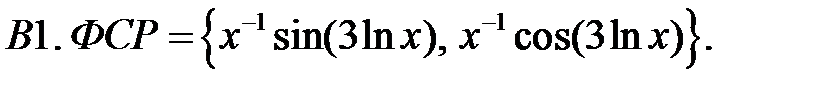
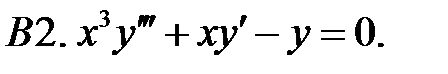
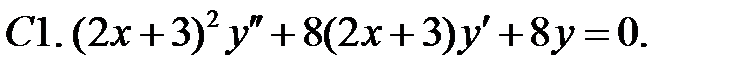
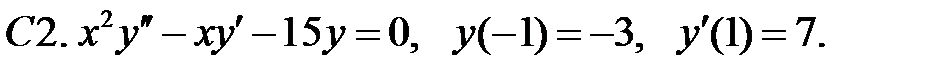
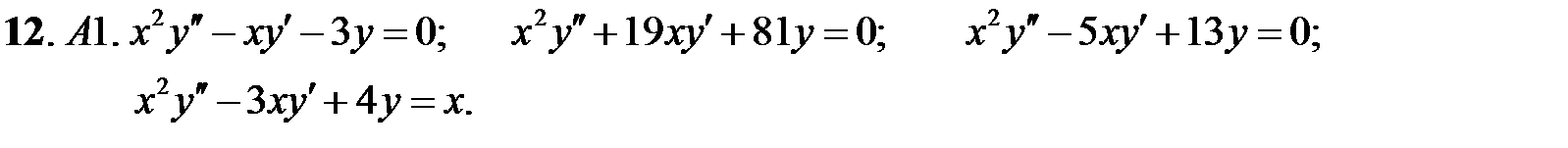
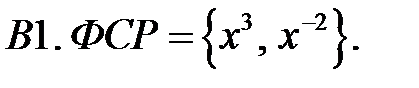
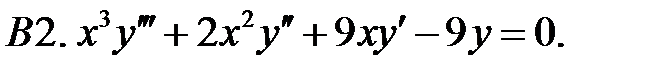
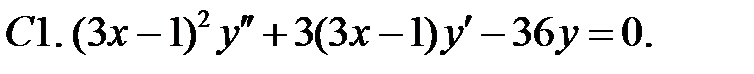
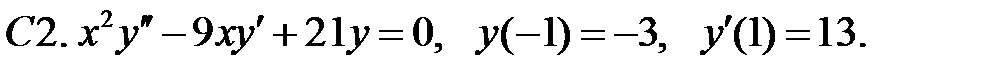
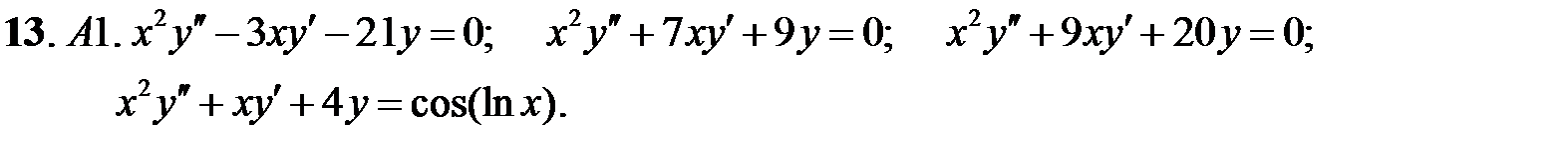
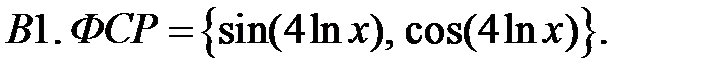
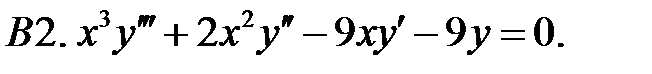
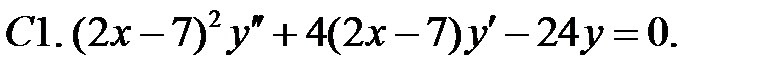
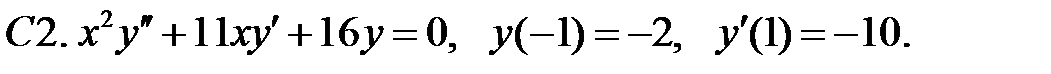
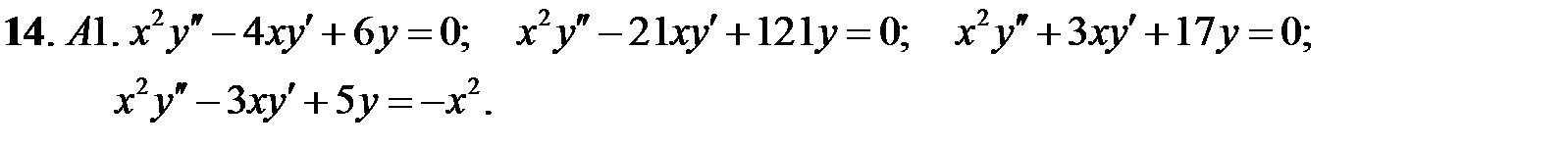
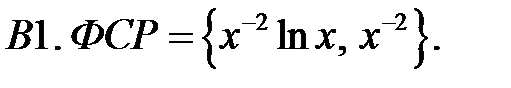
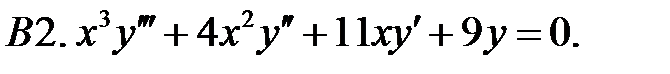
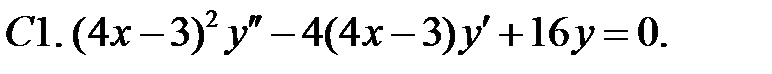
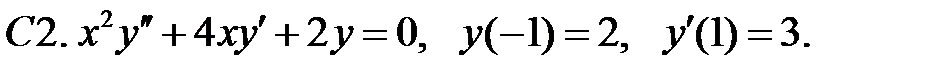
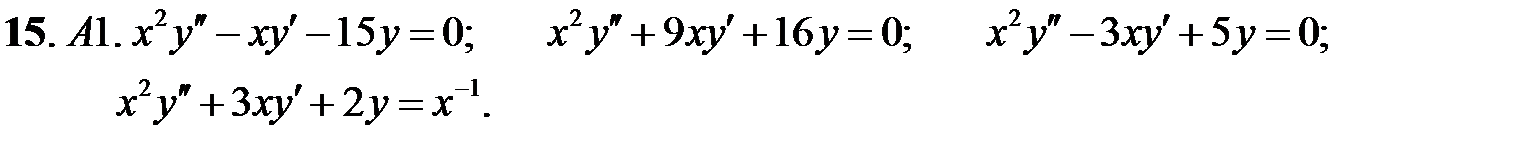
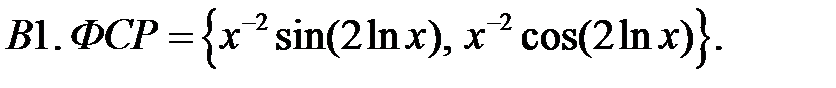
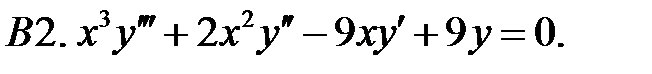
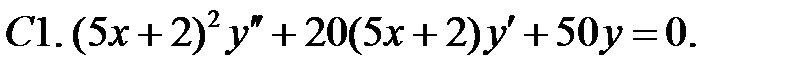
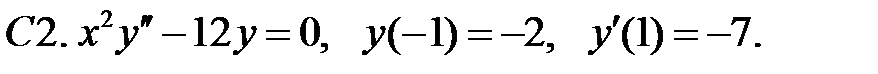
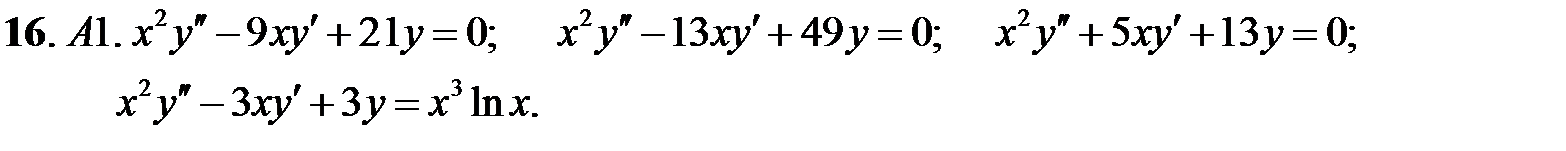
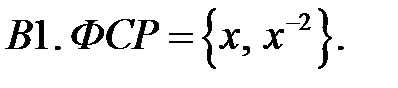
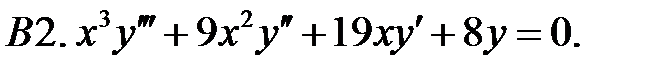
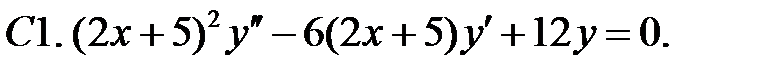
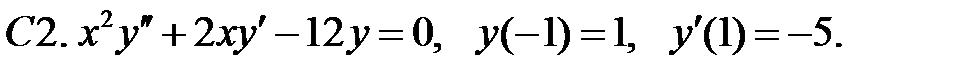
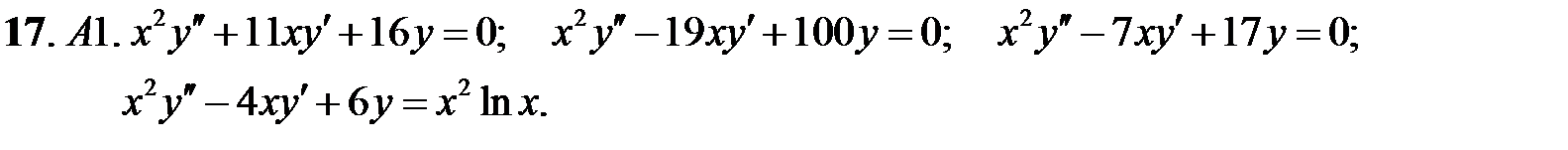
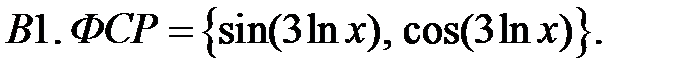
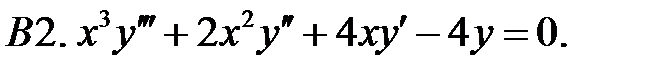
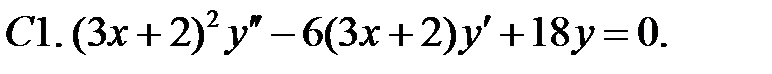
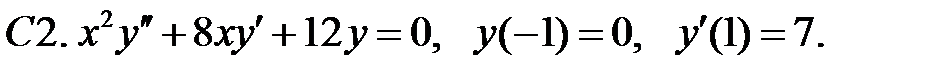
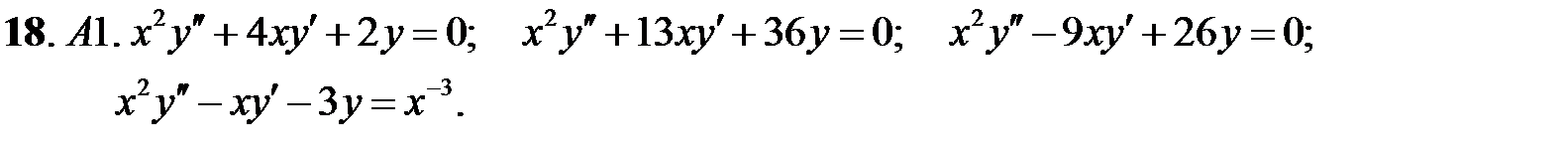
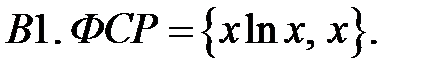
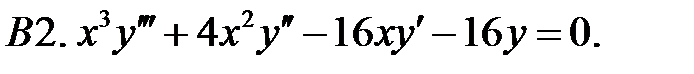
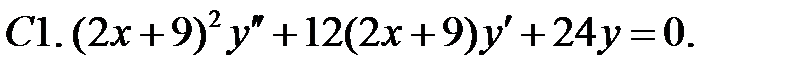
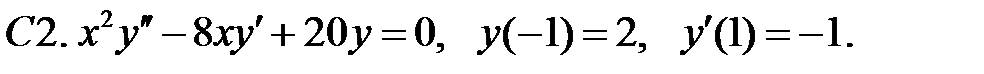
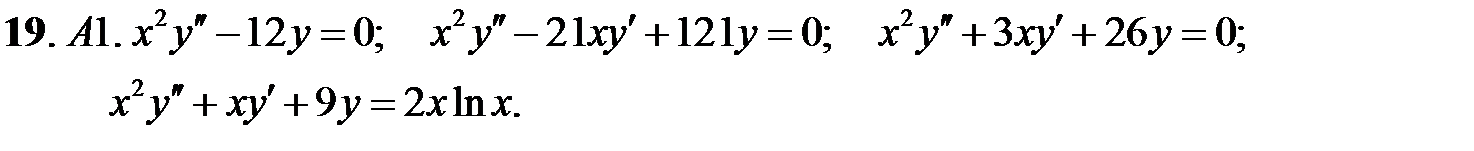
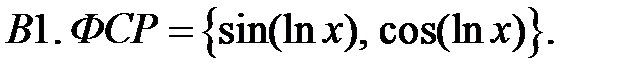
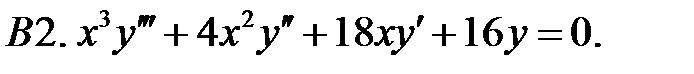
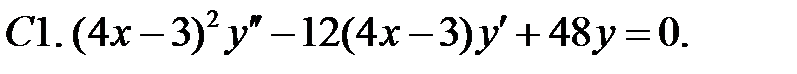
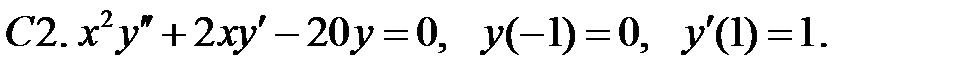
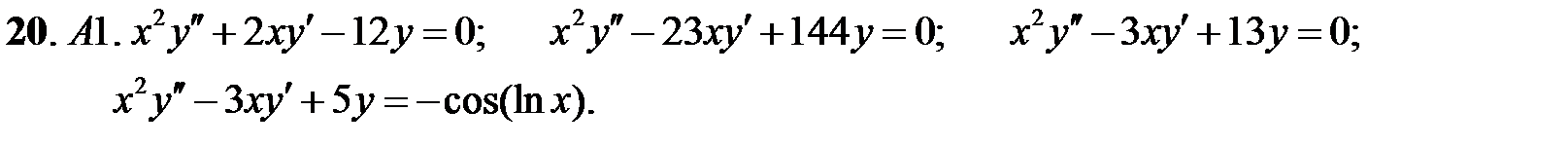
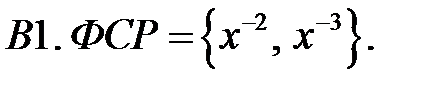
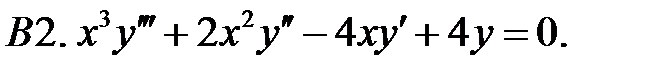
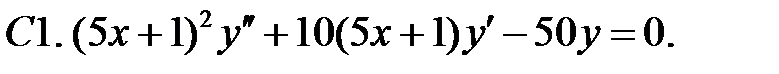
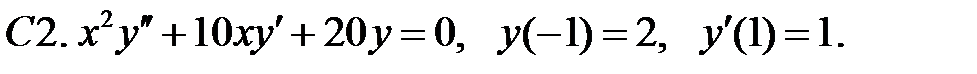
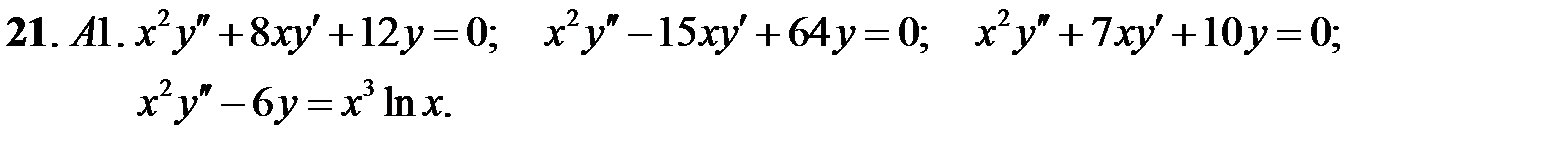
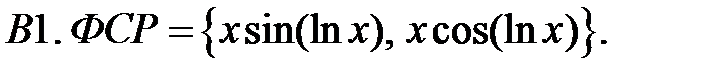
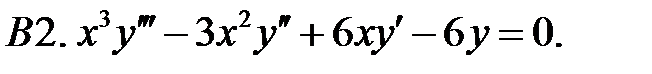
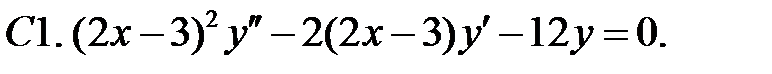
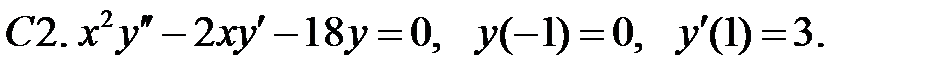
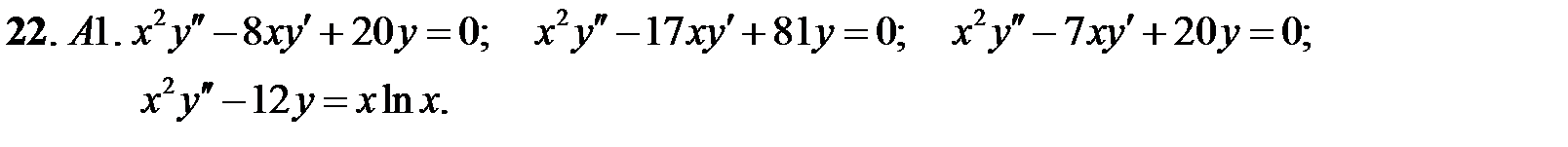
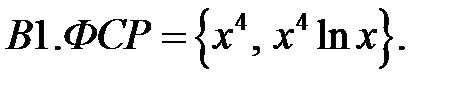
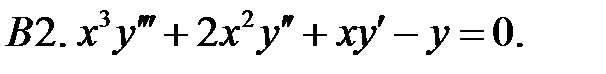
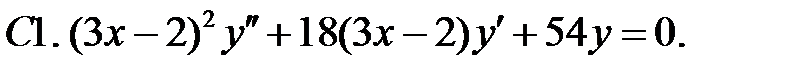
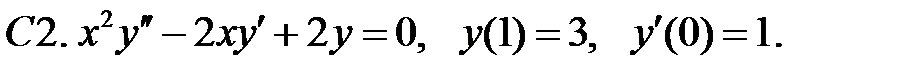
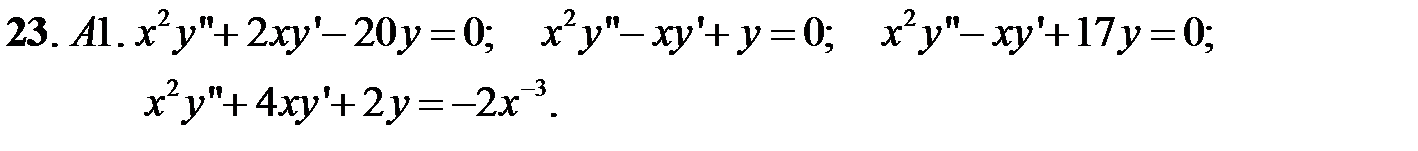
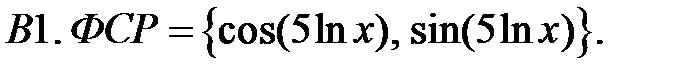
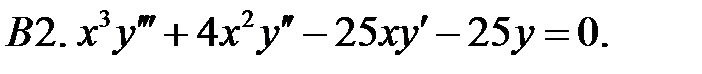
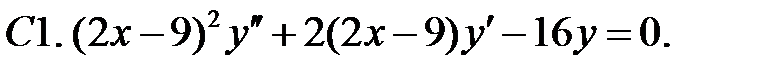
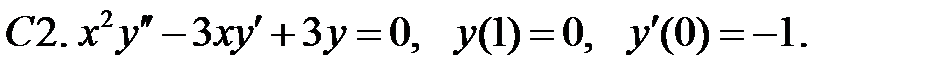
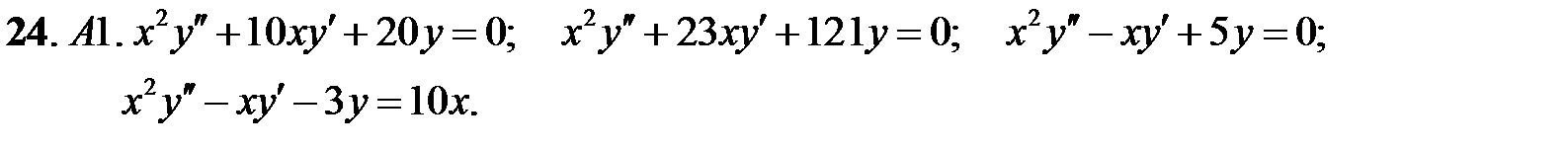
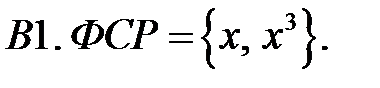
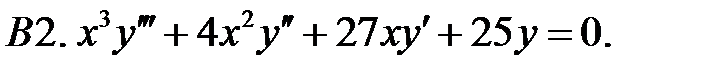
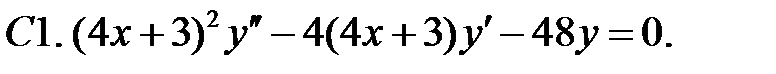
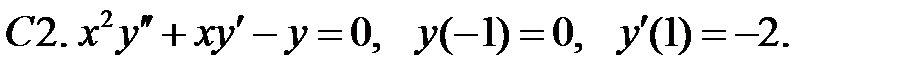
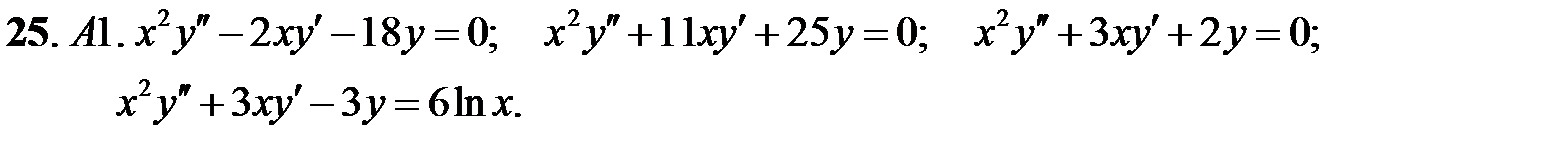
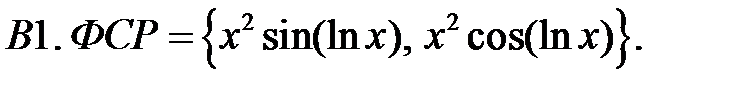
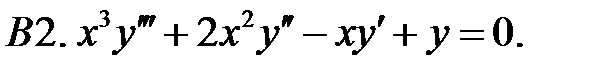
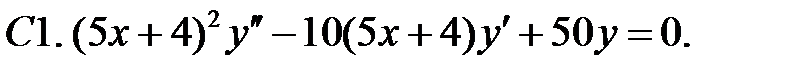
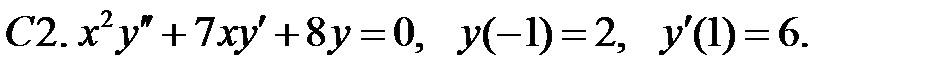
Задание № 22. Краевые задачи
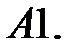 Найти решения уравнений, удовлетворяющие указанным краевым условиям.
Найти решения уравнений, удовлетворяющие указанным краевым условиям.
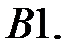 Решить краевую задачу.
Решить краевую задачу.
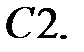 Построить функцию Грина указанной краевой задачи
Построить функцию Грина указанной краевой задачи
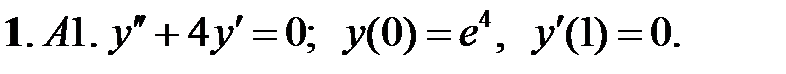
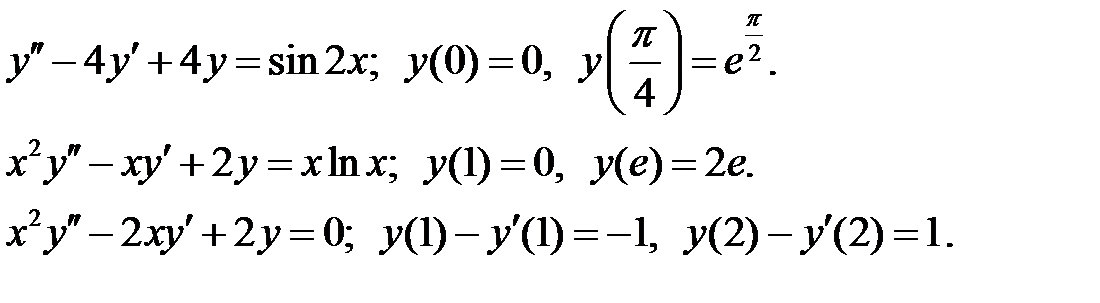
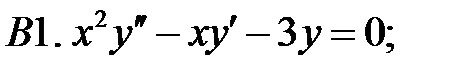
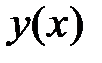 ограничено при
ограничено при 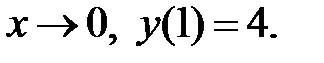
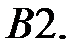 При каком
При каком  краевая задача
краевая задача 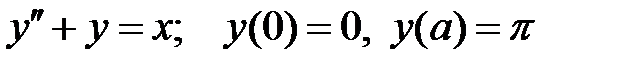 имеет бесконечное множество решений?
имеет бесконечное множество решений?
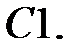 При каких
При каких 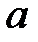 краевая задача
краевая задача 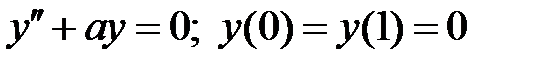 имеет тривиальное решение?
имеет тривиальное решение?
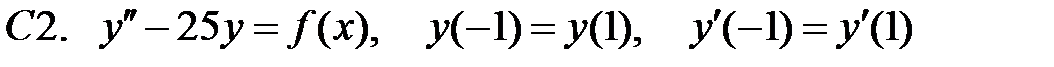 .
.

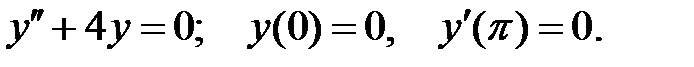
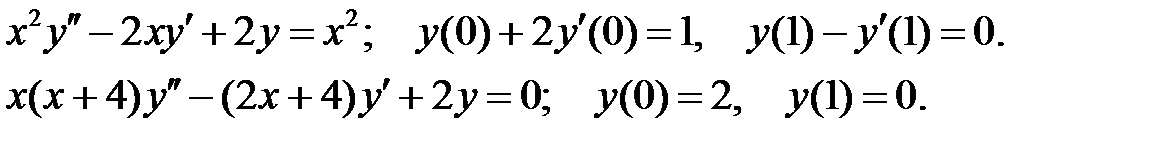
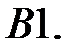
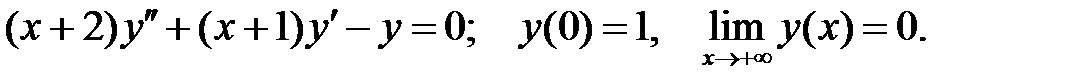
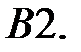 При каких
При каких 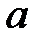 краевая задача
краевая задача 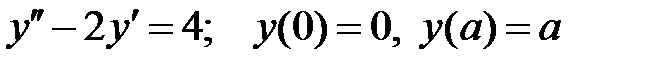 имеет единственное решение?
имеет единственное решение?
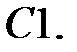 При каких
При каких 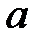 краевая задача
краевая задача 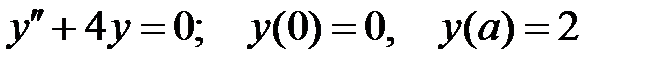 не имеет решений?
не имеет решений?
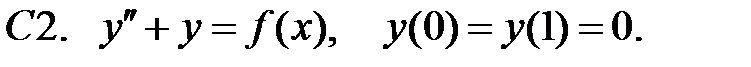
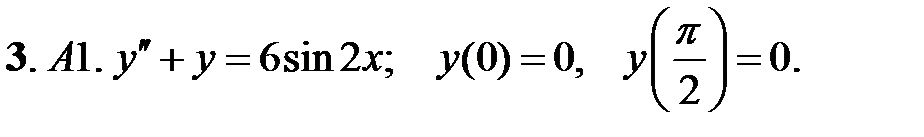
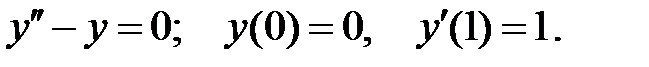
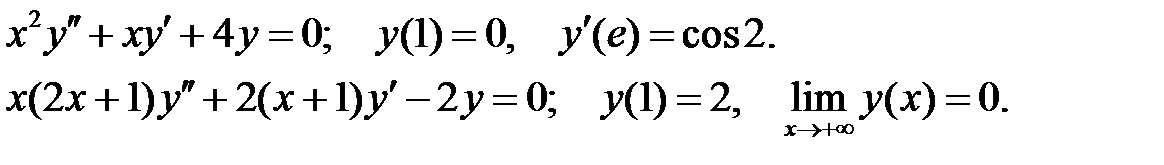
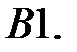
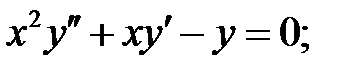
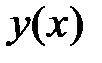 ограничено при
ограничено при 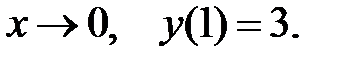
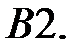 При каких
При каких 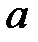 краевая задача
краевая задача 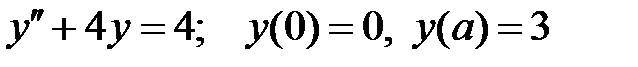 не имеет решений?
не имеет решений?
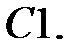 При каких
При каких 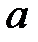 краевая задача
краевая задача 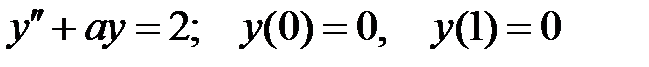 имеет единственное решение?
имеет единственное решение?
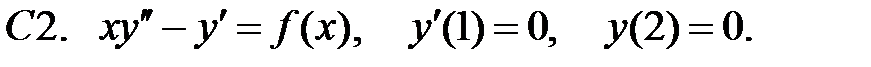
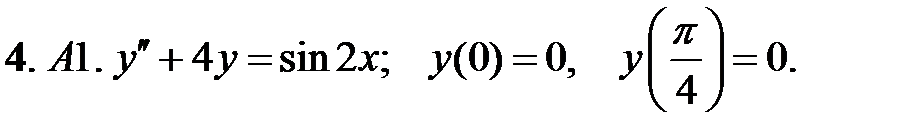
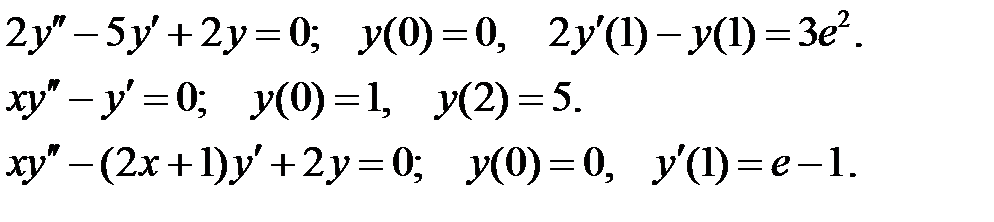
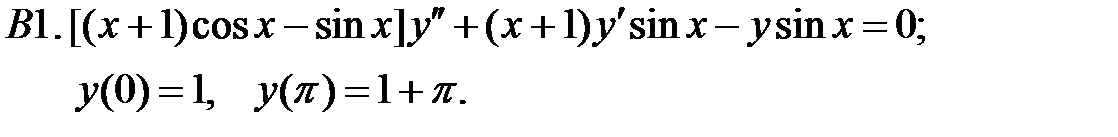
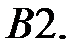 При каких
При каких 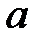 краевая задача
краевая задача 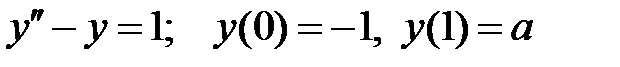 имеет только решение
имеет только решение 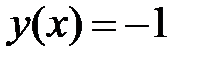 ?
?
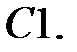 При каких
При каких 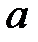 краевая задача
краевая задача 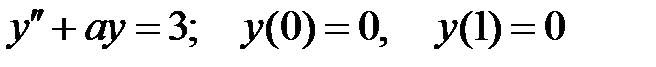 имеет бесконечное множество решений?
имеет бесконечное множество решений?
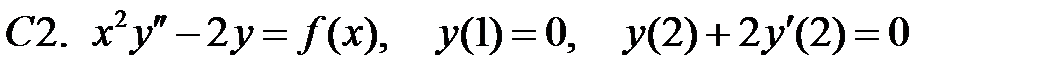 .
.
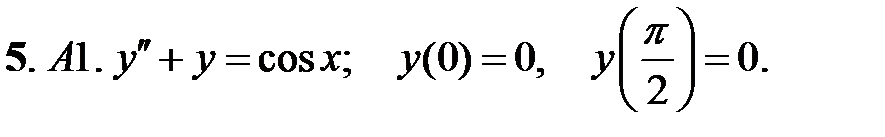
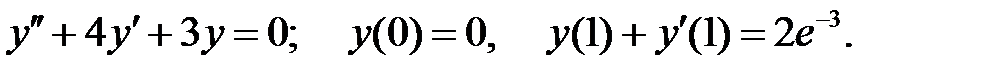
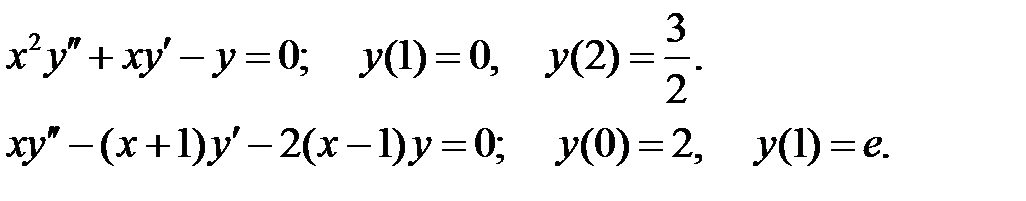
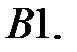
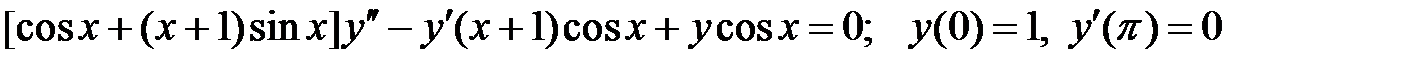 .
.
 При каких
При каких 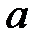 краевая задача
краевая задача 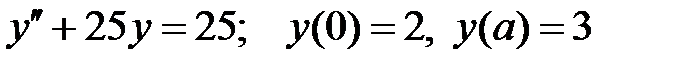 имеет единственное решение?
имеет единственное решение?
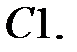 При каких
При каких 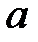 уравнение
уравнение 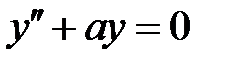 имеет ненулевое решение, удовлетворяющее условиям
имеет ненулевое решение, удовлетворяющее условиям 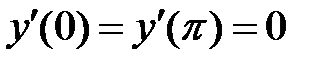 ?
?
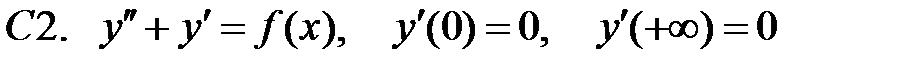 .
.
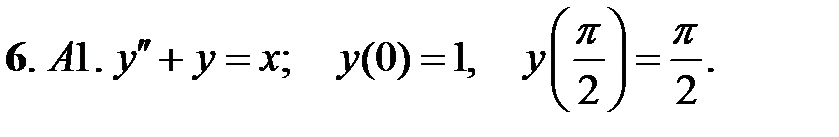
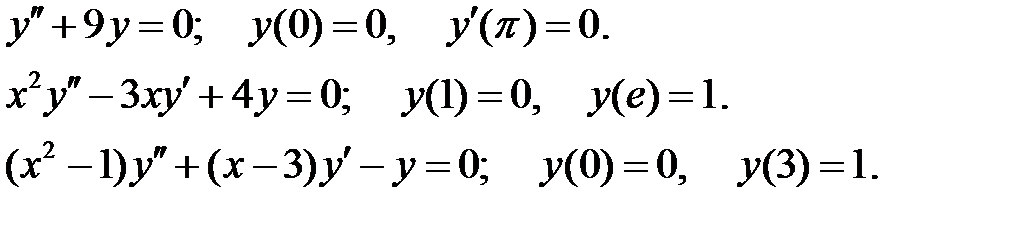
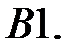
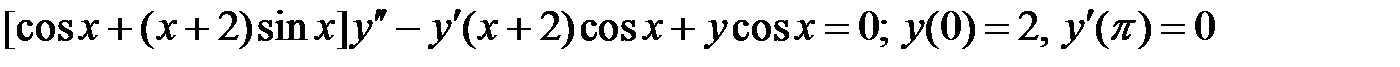 .
.
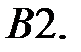 При каких
При каких 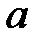 краевая задача
краевая задача 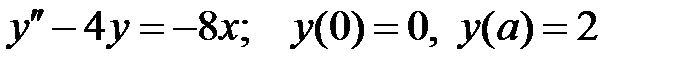 имеет единственное решение?
имеет единственное решение?
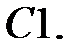 При каких
При каких 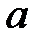 краевая задача
краевая задача 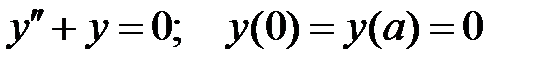 имеет бесконечное множество решений?
имеет бесконечное множество решений?
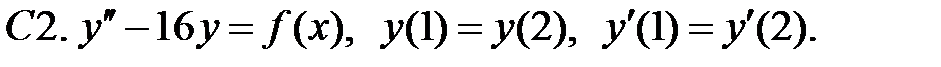
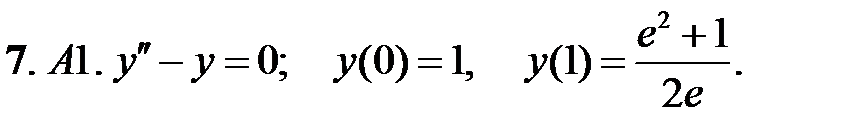
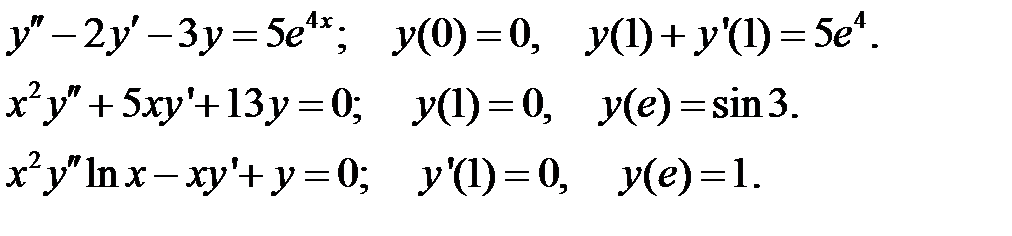
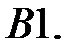
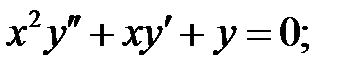
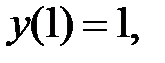
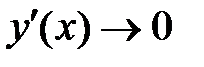 при
при 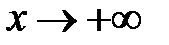 .
.
 При каких
При каких 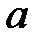 краевая задача
краевая задача 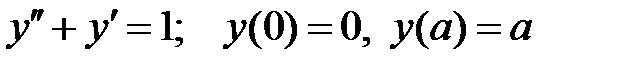 имеет решение, отличное от
имеет решение, отличное от 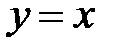 ?
?
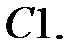 При каких
При каких 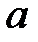 краевая задача
краевая задача 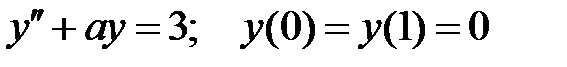 не имеет решений?
не имеет решений?
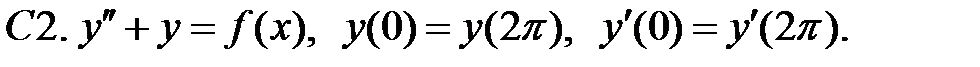
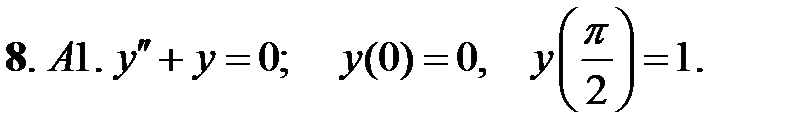
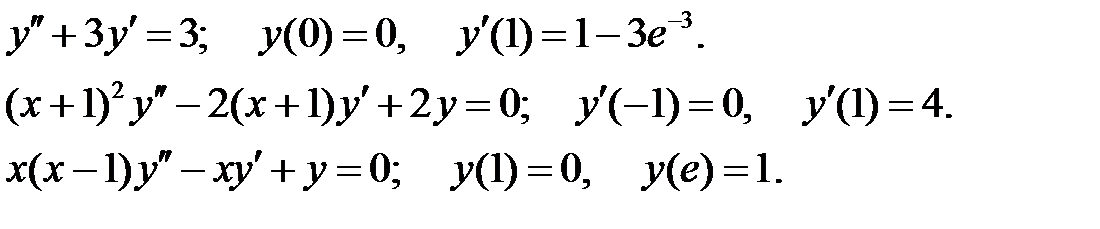
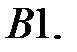
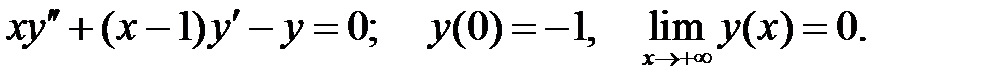
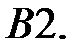 При каких
При каких 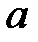 краевая задача
краевая задача 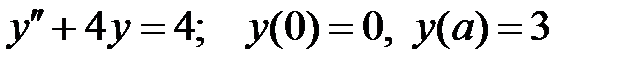 не имеет решений?
не имеет решений?
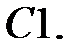 При каких
При каких 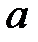 краевая задача
краевая задача 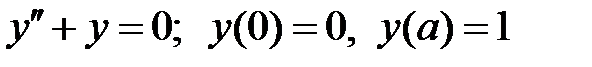 имеет единственное решение?
имеет единственное решение?
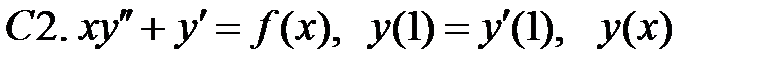 ограничено при
ограничено при 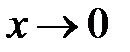 .
.
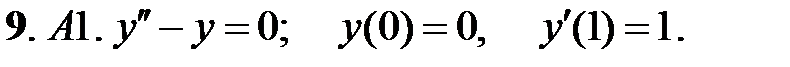
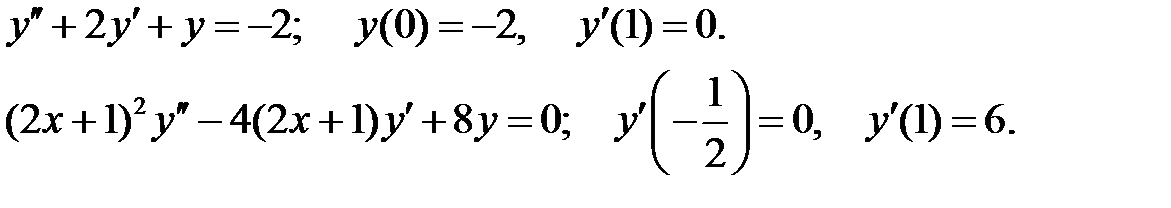
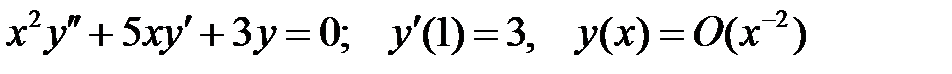 при
при 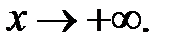
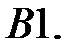
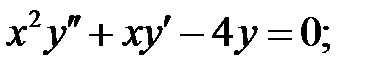
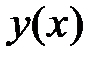 ограничено при
ограничено при 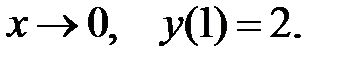
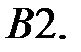 При каких
При каких 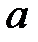 краевая задача
краевая задача 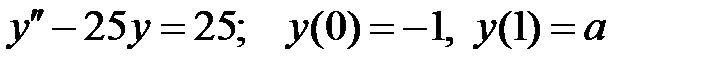 имеет только решение
имеет только решение 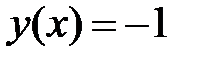 ?
?
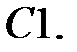 При каких
При каких 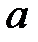 краевая задача
краевая задача 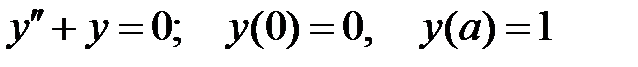 не имеет решений?
не имеет решений?
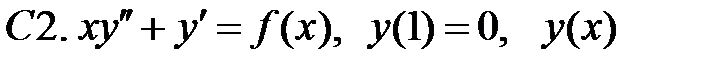 ограничено при
ограничено при 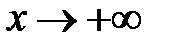 .
.
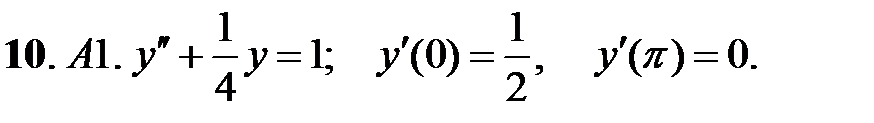
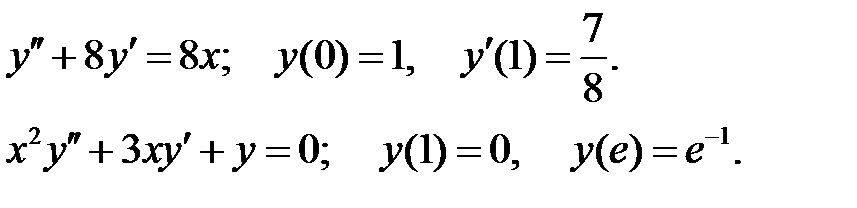
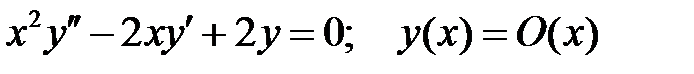 при
при 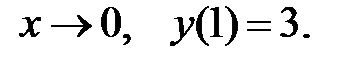
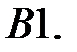
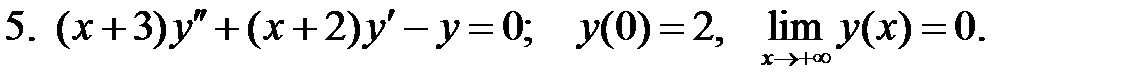
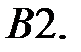 При каких
При каких 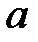 краевая задача
краевая задача 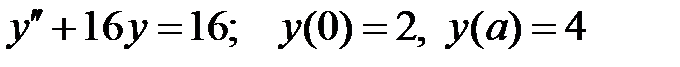 имеет единственное решение?
имеет единственное решение?
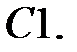 При каких
При каких 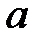 краевая задача
краевая задача 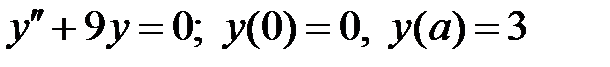 имеет единственное решение?
имеет единственное решение?
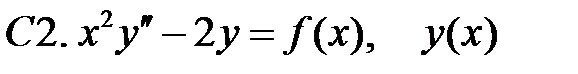 ограничена при
ограничена при 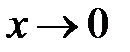 и при
и при 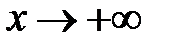 .
.
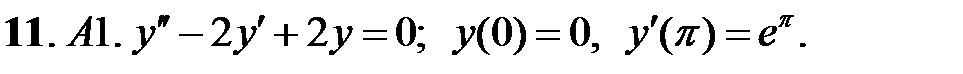
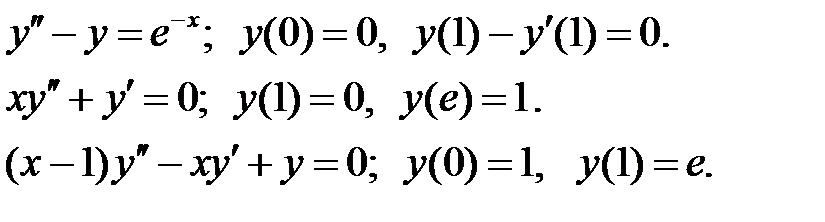
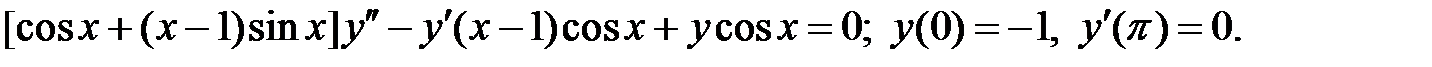
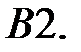 При каких
При каких 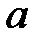 краевая задача
краевая задача 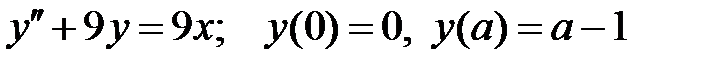 имеет бесконечное множество решений?
имеет бесконечное множество решений?
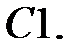 При каких
При каких 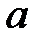 краевая задача
краевая задача 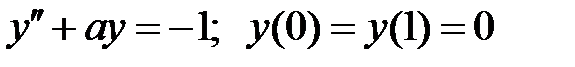 имеет единственное решение?
имеет единственное решение?
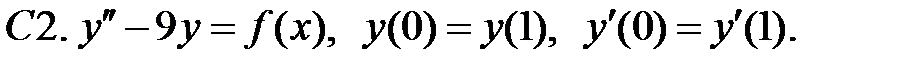
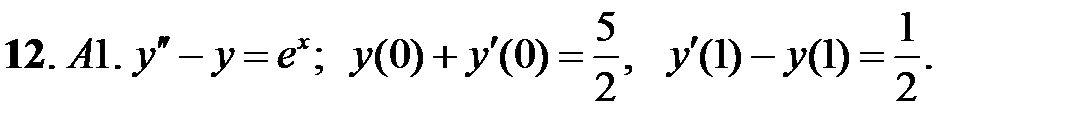
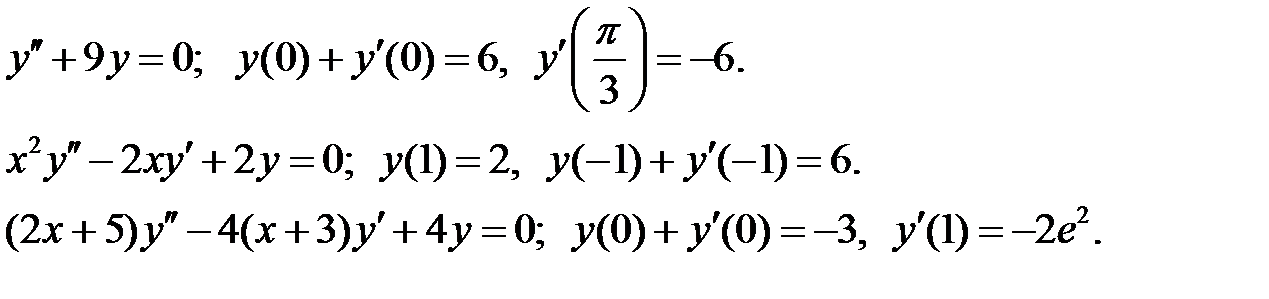
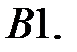
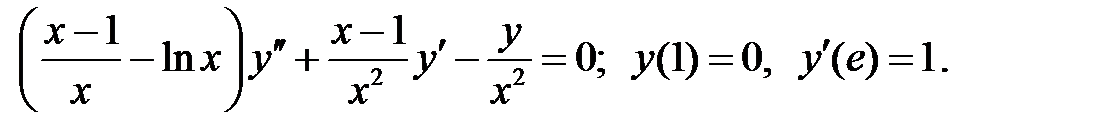
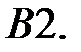 При каких
При каких 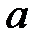 краевая задача
краевая задача 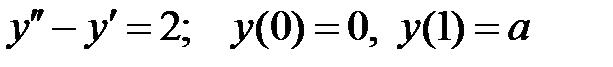 имеет единственное решение
имеет единственное решение 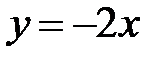 ?
?
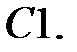 При каких
При каких 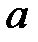 краевая задача
краевая задача 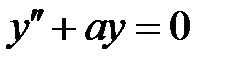 имеет ненулевое решение, удовлетворяющее условиям
имеет ненулевое решение, удовлетворяющее условиям 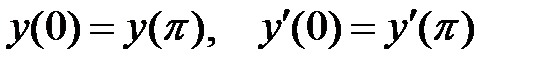 ?
?
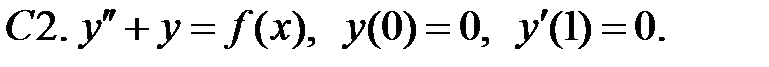
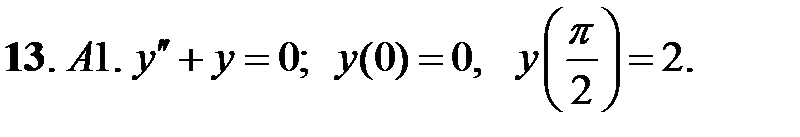
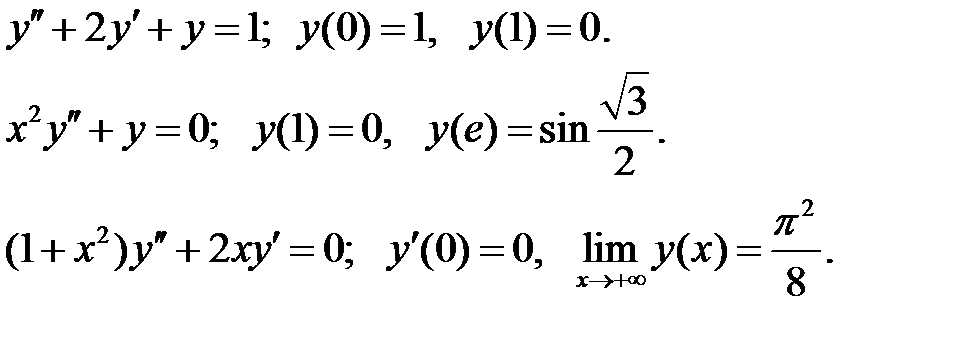
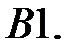
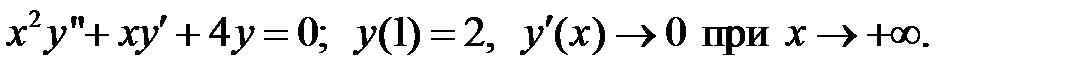
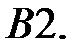 При каких
При каких 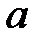 краевая задача
краевая задача 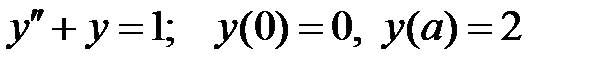 не имеет решений?
не имеет решений?
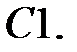 При каких
При каких 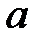 краевая задача
краевая задача 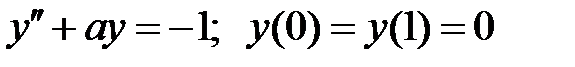 имеет единственное решение?
имеет единственное решение?
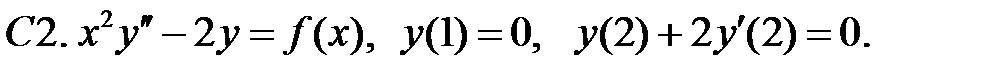
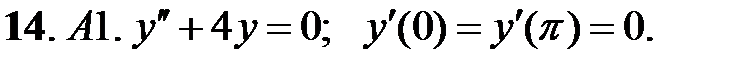
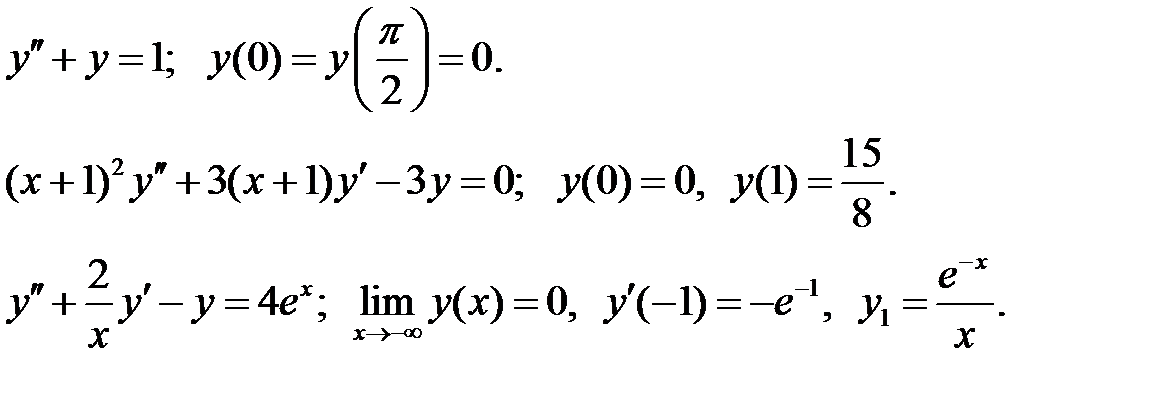
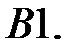
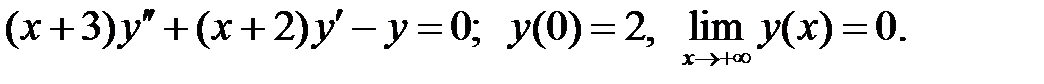
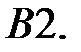 При каких
При каких 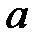 краевая задача
краевая задача 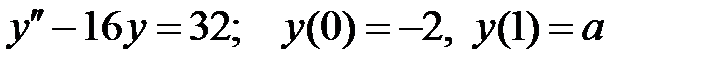 имеет единственное решение
имеет единственное решение 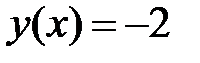 ?
?
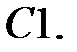 При каких
При каких 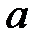 краевая задача
краевая задача 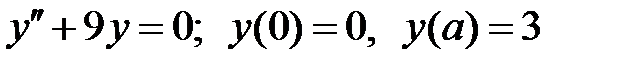 не имеет решений?
не имеет решений?
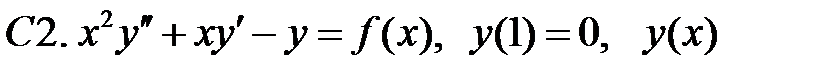 ограничено при
ограничено при 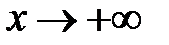 .
.
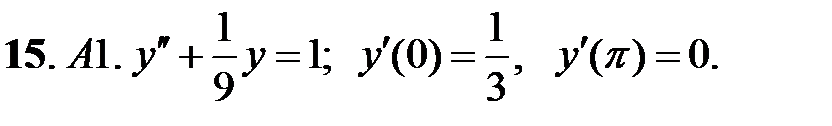
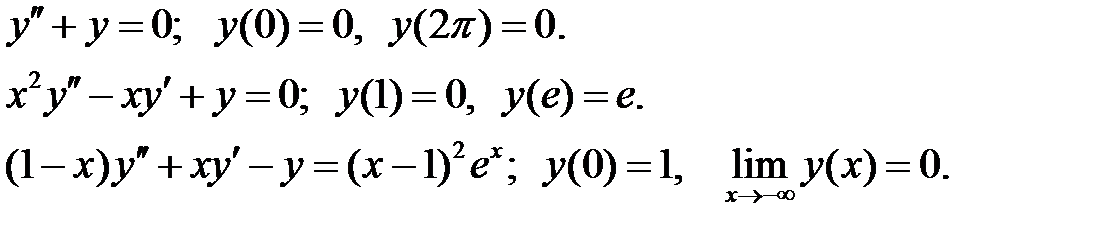
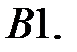
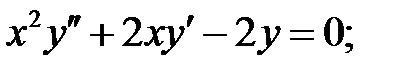
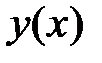 ограничено при
ограничено при 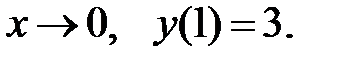
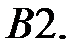 При каких
При каких 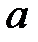 краевая задача
краевая задача 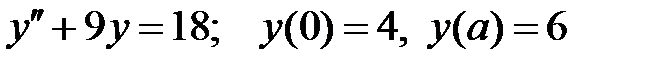 имеет единственное решение?
имеет единственное решение?
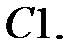 При каких
При каких 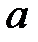 краевая задача
краевая задача 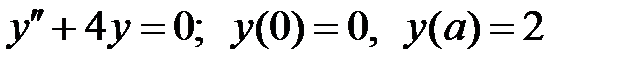 имеет единственное решение?
имеет единственное решение?
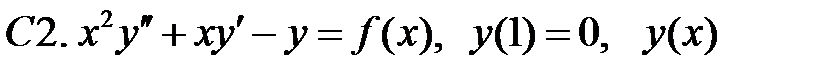 ограничена при
ограничена при 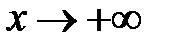 .
.
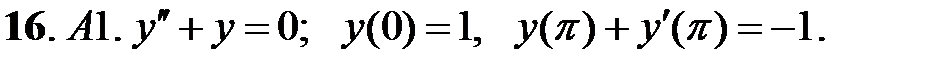
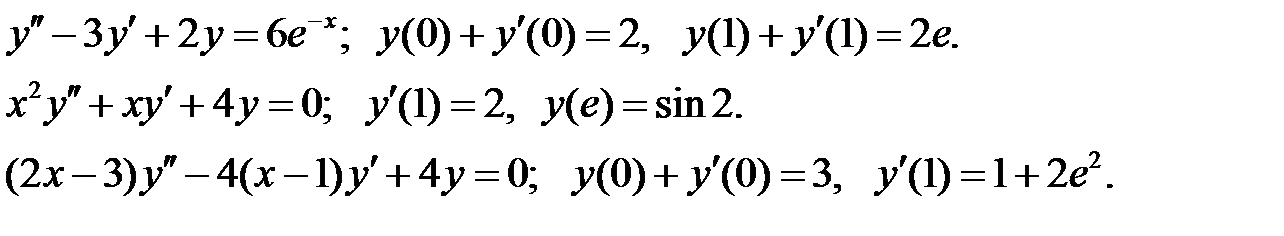
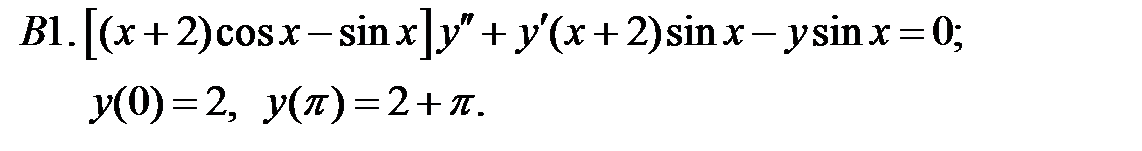
 При каких
При каких 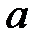 краевая задача
краевая задача 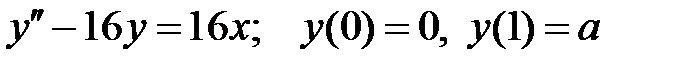 имеет единственное решение
имеет единственное решение 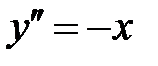 ?
?
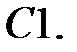 При каких
При каких 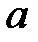 краевая задача
краевая задача 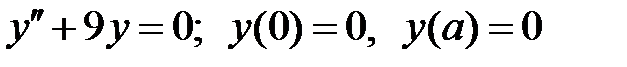 имеет бесконечное множество решений?
имеет бесконечное множество решений?
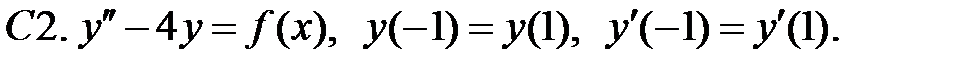
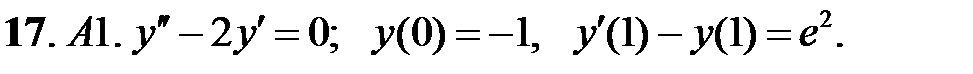
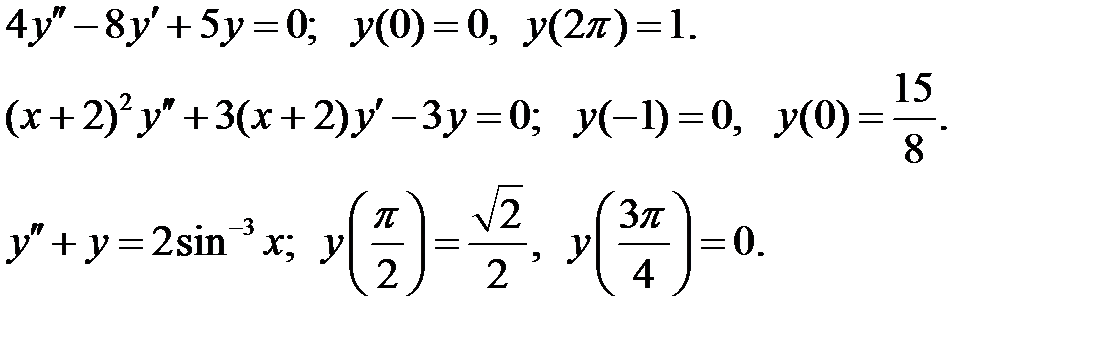
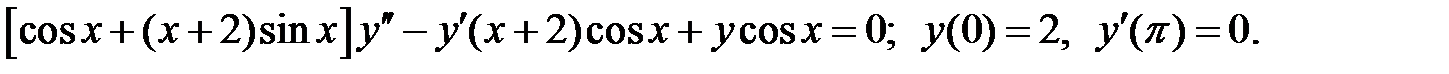
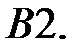 При каких
При каких 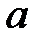 краевая задача
краевая задача 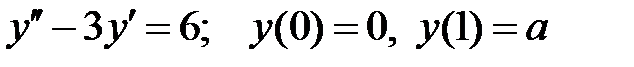 имеет единственное решение?
имеет единственное решение?
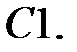 При каких
При каких 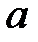 краевая задача
краевая задача 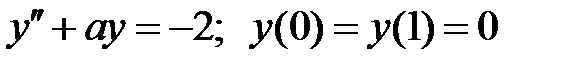 не имеет решений?
не имеет решений?
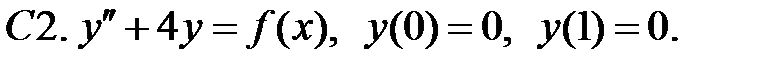
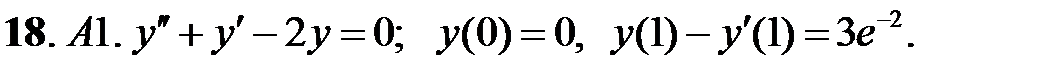
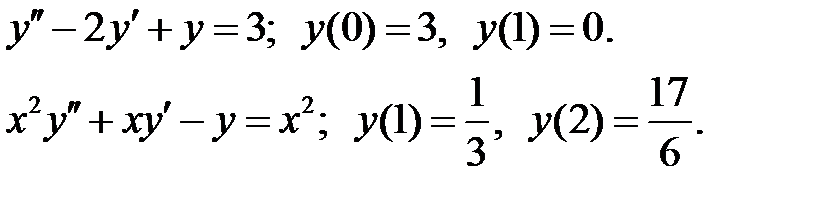
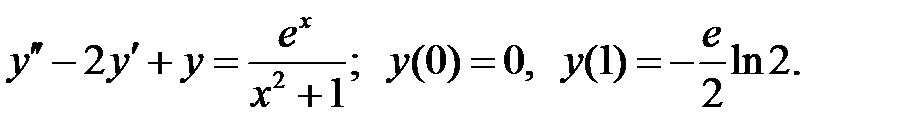
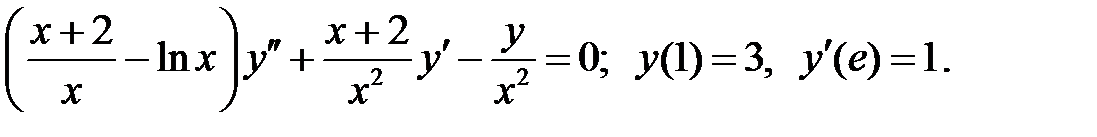
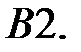 При каких
При каких 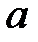 краевая задача
краевая задача 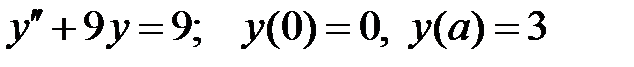 не имеет решений?
не имеет решений?
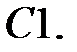 При каких
При каких 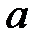 краевая задача
краевая задача 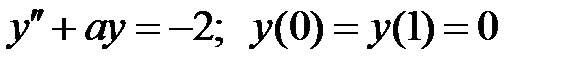 имеет единственное решение?
имеет единственное решение?
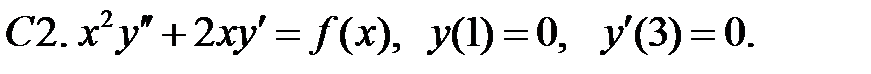
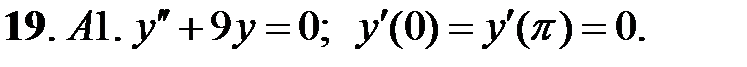
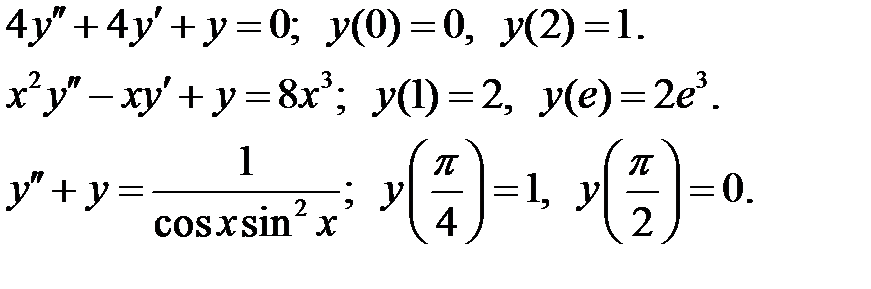
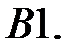
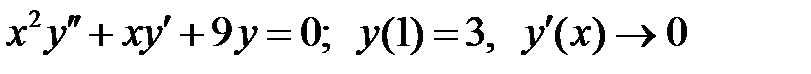 при
при 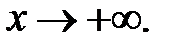
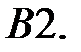 При каких
При каких 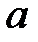 краевая задача
краевая задача 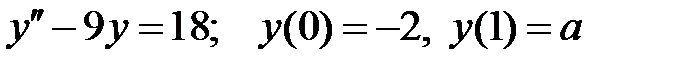 имеет единственное решение
имеет единственное решение 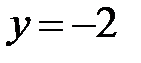 ?
?
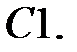 При каких
При каких 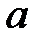 уравнение
уравнение 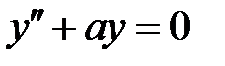 имеет ненулевое решение, удовлетворяющее условиям:
имеет ненулевое решение, удовлетворяющее условиям: 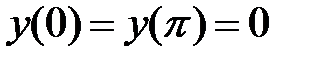 ?
?
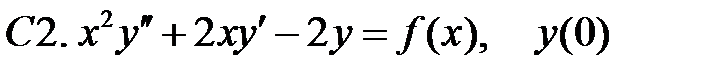 ограничено,
ограничено, 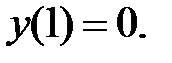
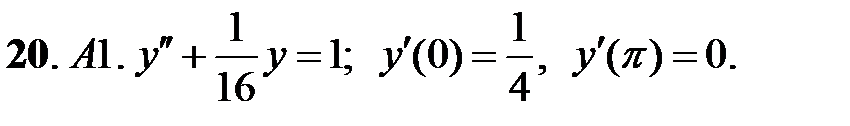
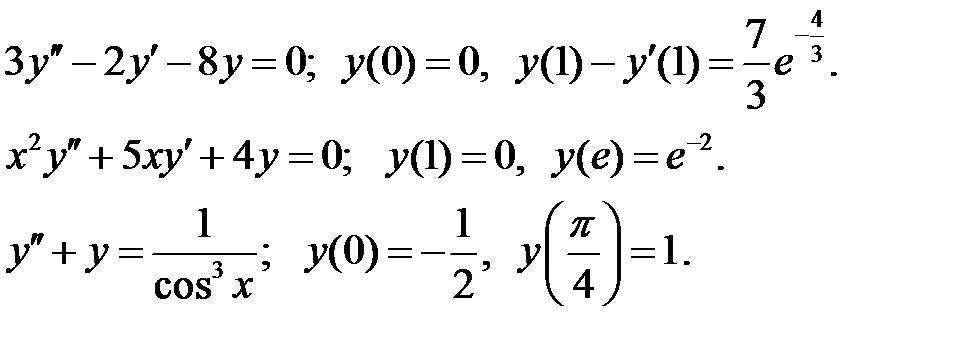
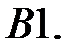
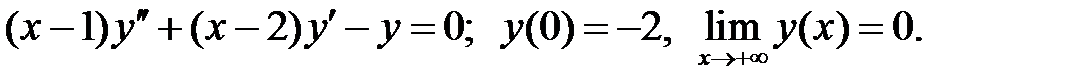
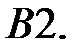 При каких
При каких 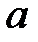 краевая задача
краевая задача 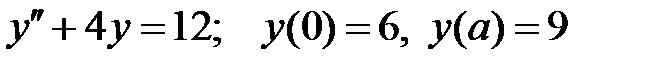 имеет единственное решение?
имеет единственное решение?
 При каких
При каких 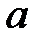 краевая задача
краевая задача 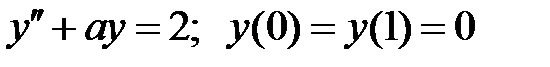 имеет бесконечное множество решений?
имеет бесконечное множество решений?
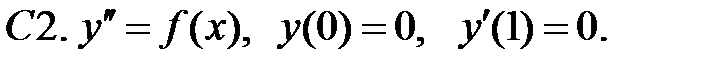
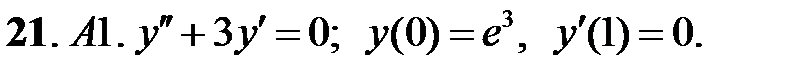
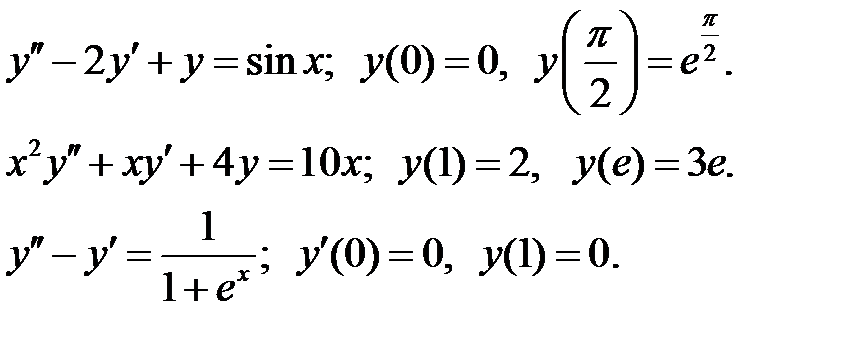
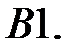
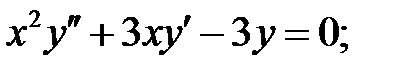
 ограничено при
ограничено при 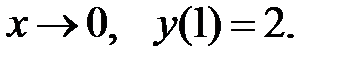
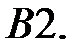 При каких
При каких 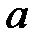 краевая задача
краевая задача 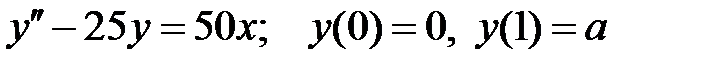 имеет единственное решение
имеет единственное решение 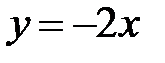 ?
?
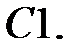 При каких
При каких 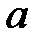 краевая задача
краевая задача 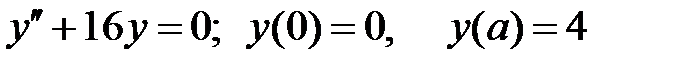 не имеет решений?
не имеет решений?
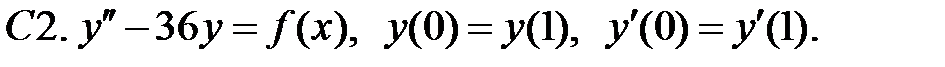
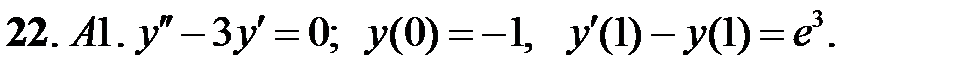
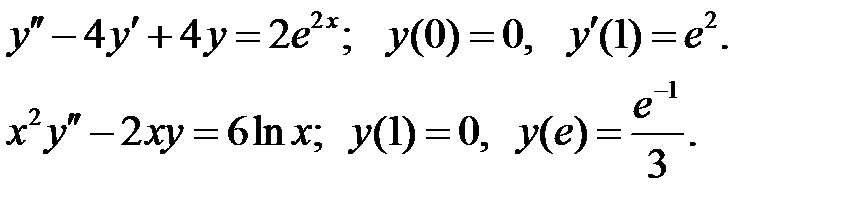
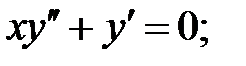
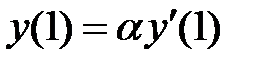 ,
, 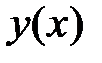 ограничено при
ограничено при 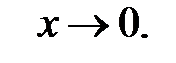
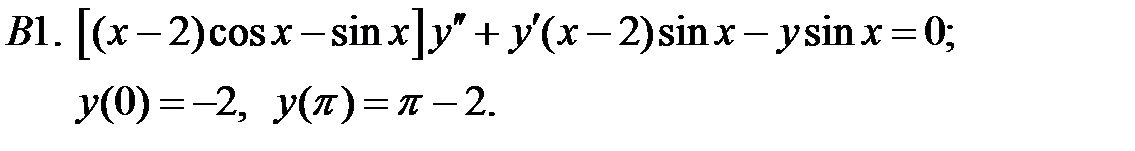
 При каких
При каких 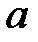 краевая задача
краевая задача 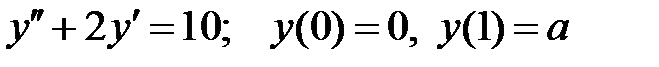 имеет единственное решение?
имеет единственное решение?
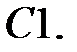 При каких
При каких 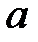 краевая задача
краевая задача 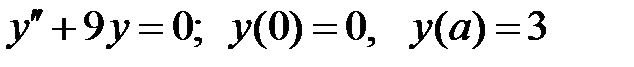 имеет единственное решение?
имеет единственное решение?
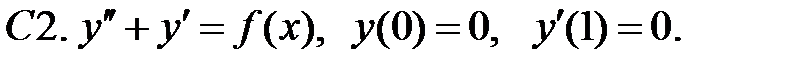
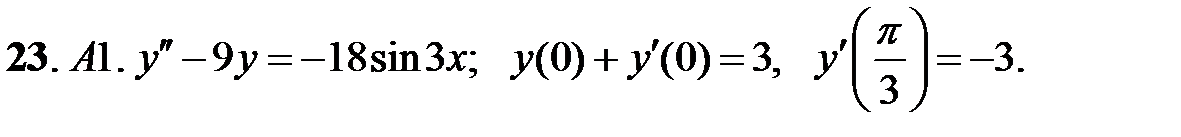
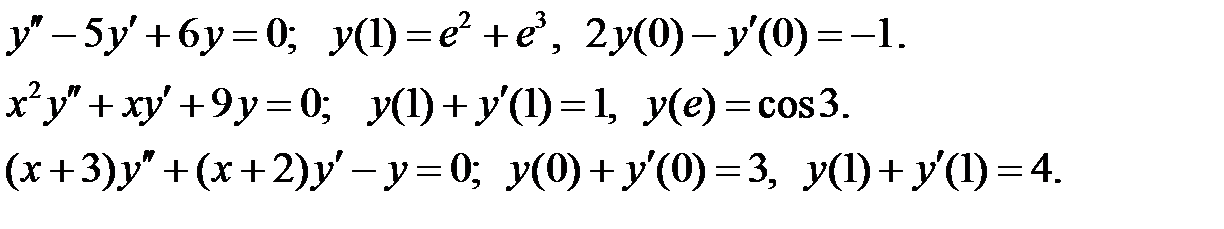
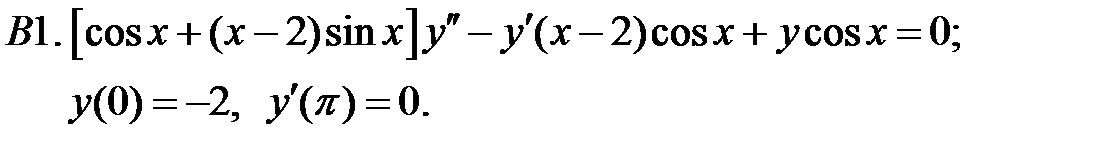
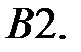 При каких
При каких 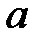 краевая задача
краевая задача 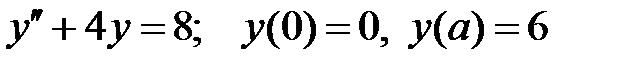 не имеет решений?
не имеет решений?
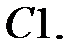 При каких
При каких 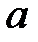 краевая задача
краевая задача 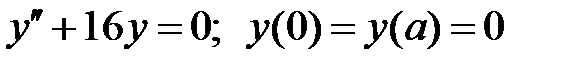 имеет бесконечное множество решений?
имеет бесконечное множество решений?
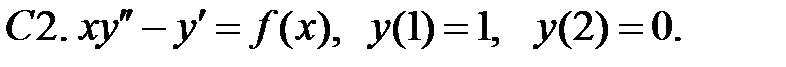
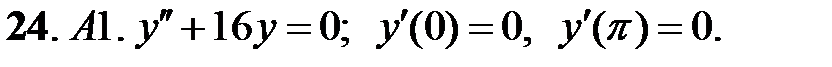
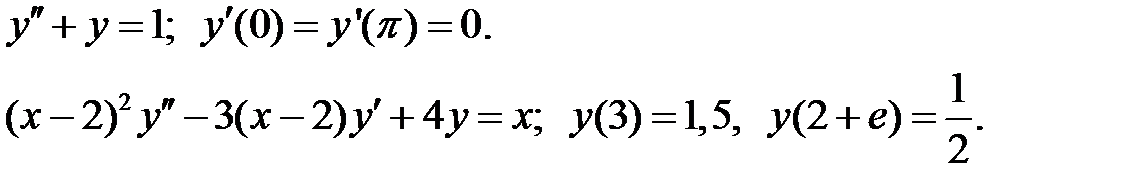
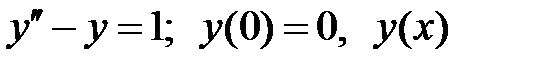 ограничено при
ограничено при 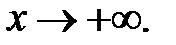
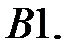
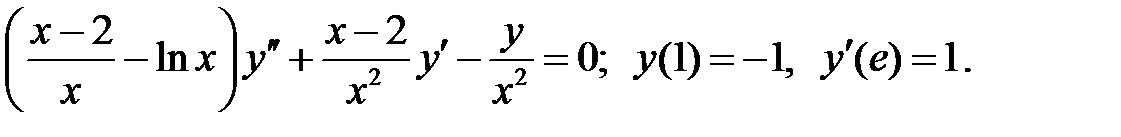
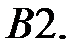 При каких
При каких 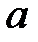 краевая задача
краевая задача 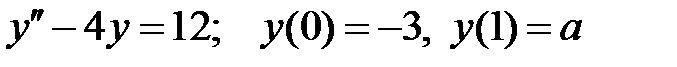 имеет единственное решение
имеет единственное решение 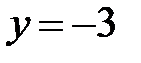 ?
?
 При каких
При каких 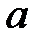 краевая задача
краевая задача 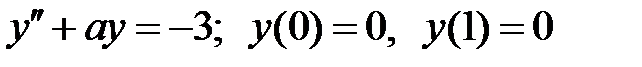 не имеет решений?
не имеет решений?
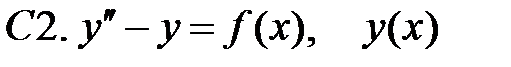 ограничено при
ограничено при 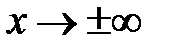 .
.
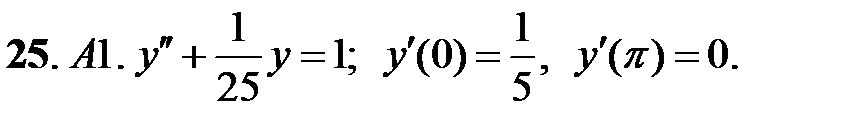
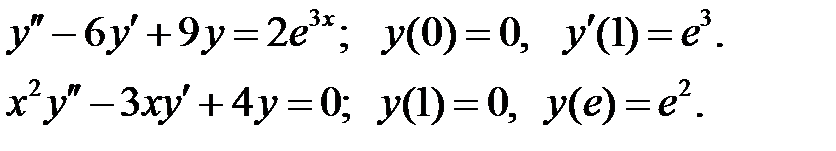
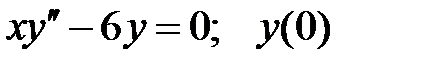 ограничено при
ограничено при 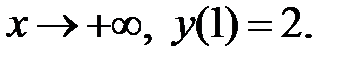
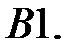
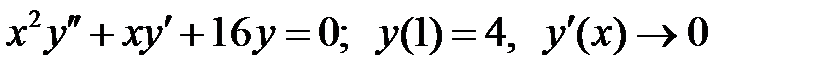 при
при 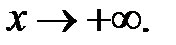
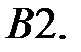 При каких
При каких 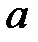 краевая задача
краевая задача 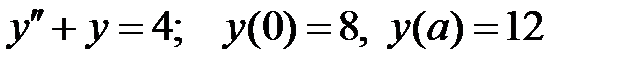 имеет единственное решение?
имеет единственное решение?
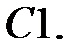 При каких
При каких 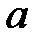 краевая задача
краевая задача 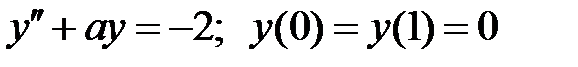 имеет бесконечное множество решений?
имеет бесконечное множество решений?
5.9. Вопросы и задачи для повторения
1. Какой общий вид имеет линейное уравнение n-го порядка? При каком условии задача Коши для линейного уравнения имеет единственное решение?
2. На каком интервале существуют решения линейного уравнения?
3. Почему линейное уравнение не имеет особых решений?
4. Может ли график ненулевого решения однородного линейного уравнения второго порядка касаться оси Ох? Может ли он пересекать ось Ох?
5. Какие решения однородного линейного уравнения называются линейно независимыми?
6. Показать, что система функций 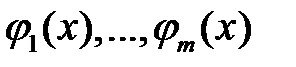 , определенных на
, определенных на 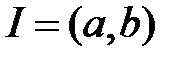 , является линейно зависимой на
, является линейно зависимой на 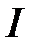 , если среди этих функций имеются по крайней мере две тождественно равные на
, если среди этих функций имеются по крайней мере две тождественно равные на 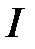 .
.
7. Показать, что любая подсистема линейно независимых на 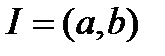 функций
функций 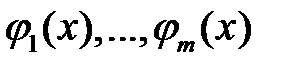 также линейно независима на
также линейно независима на 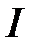 .
.
8. Показать, что система функций 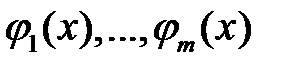 , определенных на
, определенных на 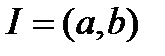 , является линейно зависимой на
, является линейно зависимой на 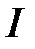 , если какая-либо подсистема этой системы линейно зависима на
, если какая-либо подсистема этой системы линейно зависима на 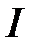 .
.
9. Показать, что если система функций 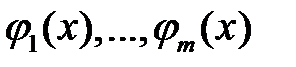 , определенных на
, определенных на 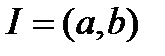 , линейно зависима на
, линейно зависима на 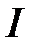 , то она линейно зависима на любом промежутке
, то она линейно зависима на любом промежутке 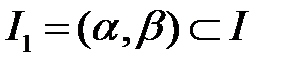 .
.
10. Пусть функции 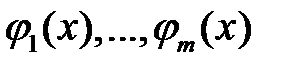 , определенные на
, определенные на 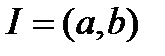 , линейно независимы на I. Следует ли отсюда, что функции
, линейно независимы на I. Следует ли отсюда, что функции 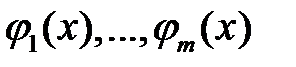 линейно независимы на любом промежутке
линейно независимы на любом промежутке 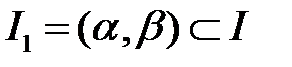 ?
?
11. Пусть функции 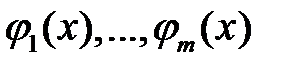 определены на промежутке
определены на промежутке 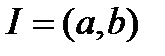 и линейно независимы на промежутке
и линейно независимы на промежутке 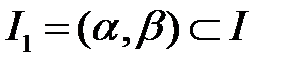 . Доказать, что функции
. Доказать, что функции 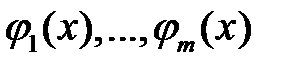 линейно независимы на I.
линейно независимы на I.
12. Исследовать на линейную зависимость функции:
1) 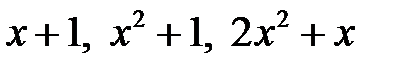 ; 2)
; 2) 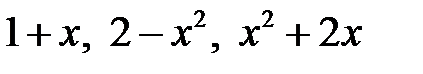 ;
;
3) 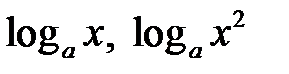 ; 4)
; 4) 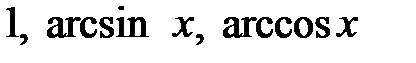 .
.
13. Найти все 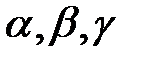 , при которых три функции
, при которых три функции 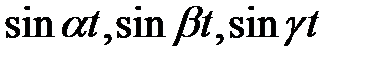 линейно зависимы.
линейно зависимы.
14. Показать, что данные функции линейно независимы, а их детерминант Вронского тождественно равен нулю; построить графики этих функций:
1) 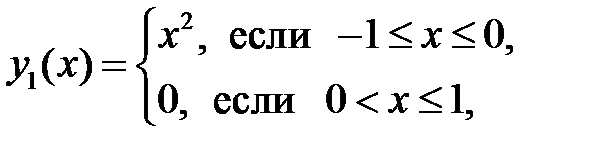
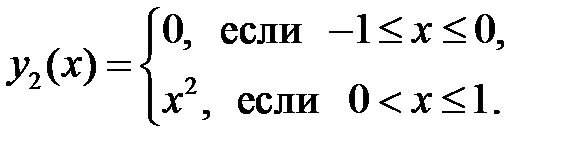
2) 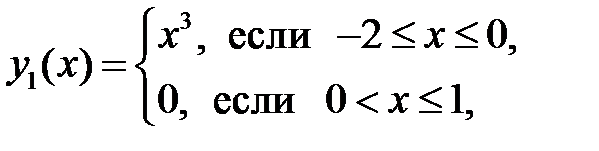
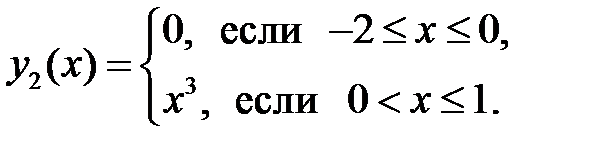
15. Известно, что для функций 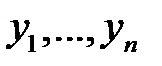 детерминант Вронского в точке
детерминант Вронского в точке 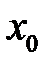 равен нулю, а в точке
равен нулю, а в точке 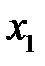 не равен нулю. Можно ли что-нибудь сказать о линейной зависимости (или независимости) этих функций на отрезке
не равен нулю. Можно ли что-нибудь сказать о линейной зависимости (или независимости) этих функций на отрезке 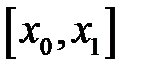 ?
?
16. Детерминант Вронского для функций 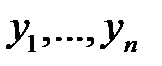 равен нулю при всех х. Могут ли быть эти функции линейно зависимыми? Линейно независимыми?
равен нулю при всех х. Могут ли быть эти функции линейно зависимыми? Линейно независимыми?
17. Что можно сказать о детерминанте Вронского функций 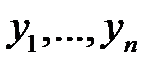 , если только известно: а) что они линейно зависимы? б) что они линейно независимы?
, если только известно: а) что они линейно зависимы? б) что они линейно независимы?
18. Для любых ли систем функций можно построить определитель Вронского?
19. Для любых ли систем вектор-функций можно построить определитель Вронского?
20. Что такое фундаментальная система решений? Может ли нулевое решение входить в состав фундаментальной системы решений?
21. Сколько фундаментальных систем решений имеет заданное однородное линейное уравнение?
22. Какое условие является необходимым и достаточным для того, чтобы данная система решений была фундаментальной?
23. Можно ли построить фундаментальную систему решений для линейного уравнения 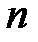 -го порядка, зная
-го порядка, зная 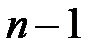 линейно независимых решений однородного уравнения?
линейно независимых решений однородного уравнения?
24. Пусть 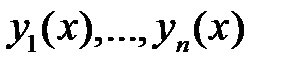 есть линейно независимая на интервале
есть линейно независимая на интервале 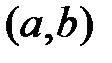 система функций такая, что её определитель Вронского существует и нигде на
система функций такая, что её определитель Вронского существует и нигде на 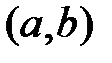 не обращается в нуль. Существует ли линейное однородное уравнение, для которого данная система является фундаментальной системой решений?
не обращается в нуль. Существует ли линейное однородное уравнение, для которого данная система является фундаментальной системой решений?
25. Существует ли линейное однородное уравнение, фундаментальной системы решений которого будут функции 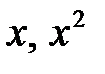 , и только они, если искомое уравнение имеет
, и только они, если искомое уравнение имеет
а) только постоянные действительные коэффициенты?
б) переменные вещественные коэффициенты?
26. Как построить общее решение однородного линейного уравнения, если известно фундаментальная система решений? В какой области определено общее решение?
27. Как решить задачу Коши при помощи формулы общего решения?
28. Как найти общее решение неоднородного линейного уравнения, если известно одно частное решение его и общее решение соответствующего однородного уравнения?
29. В чем состоит метод Лагранжа нахождения общего решения неоднородного линейного уравнения?
30. Можно ли, зная фундаментальную систему решений однородного линейного обыкновенного дифференциального уравнения 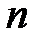 -го порядка, построить общее решение неоднородного?
-го порядка, построить общее решение неоднородного?
31. Как построить однородное линейное уравнение, имеющее заданную фундаментальную систему решений?
32. Каков минимальный порядок линейного уравнения с действительными постоянными коэффициентами, в фундаментальную систему решений которого входят функции 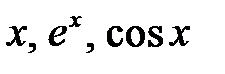 ?
?
33. В чем состоит метод Эйлера интегрирования однородных линейных уравнений с постоянными коэффициентами? Как зависит структура фундаментальной системы решений от вида корней характеристического уравнения? В какой области определено общее решение?
34. В каких случаях и в каком виде может быть найдено частное решение неоднородного линейного уравнения методом неопределенных коэффициентов?
35. Как можно найти все решения линейного уравнения с постоянными комплексными коэффициентами?
36. Как интегрируется линейное уравнение Эйлера?
37. Могут ли все решения линейного уравнения 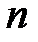 -го порядка быть периодическими функциями?
-го порядка быть периодическими функциями?
38. Какой заменой искомой функции можно избавиться в однородном линейном уравнении второго порядка от члена, содержащего первую производную от искомой функции?
39. Заменой независимой переменной 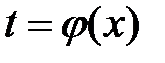 уничтожить член с первой производной в уравнении
уничтожить член с первой производной в уравнении
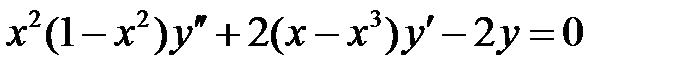 .
.
40. Какой подстановкой можно привести однородное линейное уравнение второго порядка к уравнению Риккати?
41. Как найти общее решение однородного линейного уравнения второго порядка при помощи степенных рядов? В какой области сходится ряд, представляющий решение?
42. При каком условии однородное линейное уравнение второго порядка имеет в окрестности особой точки 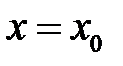 хотя бы одно частное решение в виде обобщенного степенного ряда? В какой области сходится этот ряд? В каком случае, разыскивая решение в виде обобщенного степенного ряда, получают решение в виде обычного степенного ряда? Как зависит вид второго частного решения от характера корней характеристического уравнения? В каком случае второе частное решение заведомо содержит
хотя бы одно частное решение в виде обобщенного степенного ряда? В какой области сходится этот ряд? В каком случае, разыскивая решение в виде обобщенного степенного ряда, получают решение в виде обычного степенного ряда? Как зависит вид второго частного решения от характера корней характеристического уравнения? В каком случае второе частное решение заведомо содержит 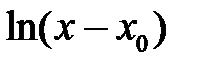 ?
?
43. Выяснить, являются ли решения 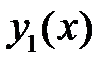 и
и 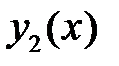 уравнения
уравнения
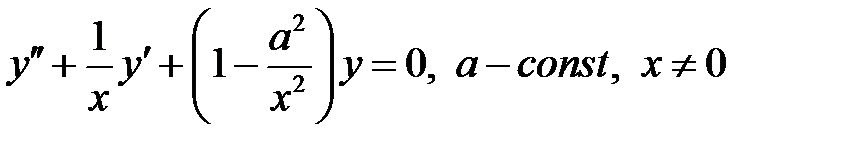
линейно независимыми на промежутке 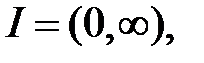 если известно, что:
если известно, что:
а) 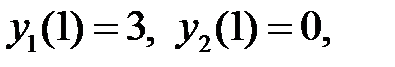 б)
б) 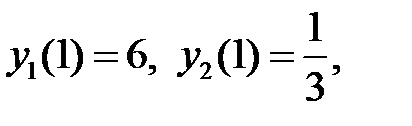 ,
,
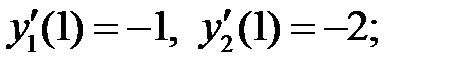
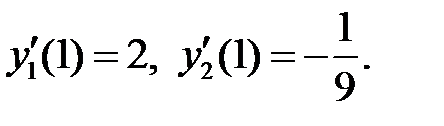
Найти 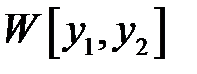 .
.
44. Если для однородного линейного уравнения второго порядка известно одно ненулевое частное решение 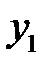 , то как найти второе частное решение
, то как найти второе частное решение 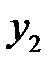 (т.е. решение линейно-независимое с
(т.е. решение линейно-независимое с 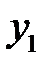 )?
)?
45. Могут ли графики двух решений уравнения
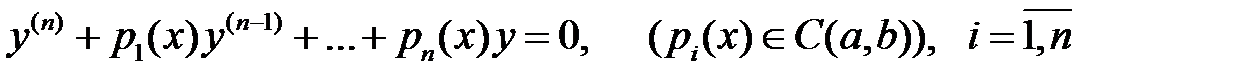
на плоскости 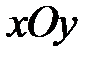 : а) пересекаться; б) касаться друг друга?
: а) пересекаться; б) касаться друг друга?
46. При каких 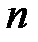 уравнение
уравнение 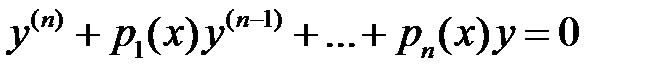 с непрерывными коэффициентами может иметь частное решение
с непрерывными коэффициентами может иметь частное решение 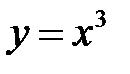 ?
?
47. Даны четыре решения уравнения 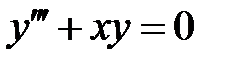 , графики которых касаются друг друга в одной точке. Сколько среди этих решений линейно-независимых?
, графики которых касаются друг друга в одной точке. Сколько среди этих решений линейно-независимых?
48. Где могут лежать точки перегиба графиков решений уравнения 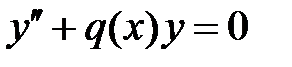 ?
?
49. Доказать, что в случае 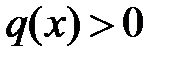 для любого решения уравнений
для любого решения уравнений 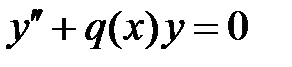 отношение
отношение 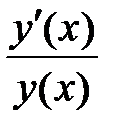 убывает при возрастании x на интервале, где
убывает при возрастании x на интервале, где 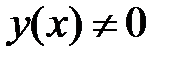 .
.
50. Доказать, что в случае 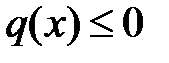 все решения уравнения
все решения уравнения 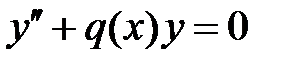 с положительными начальными условиями
с положительными начальными условиями 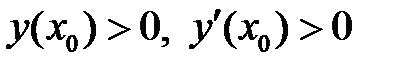 остаются положительными при всех
остаются положительными при всех 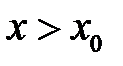 .
.
51. Пусть функции 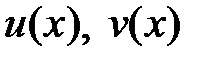 являются соответственно решениями уравнений
являются соответственно решениями уравнений 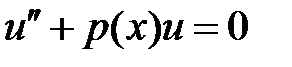 и
и 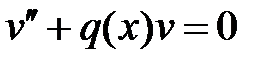 , удовлетворяющими условию
, удовлетворяющими условию 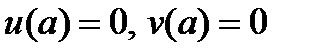 (
( 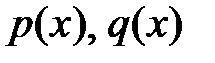 - непрерывны на отрезке
- непрерывны на отрезке 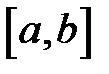 ). Доказать, что детерминант Вронского этих решений будет равен
). Доказать, что детерминант Вронского этих решений будет равен
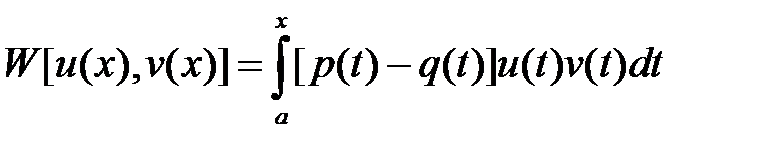 .
.
52. Найти все уравнения вида 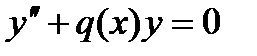 , приводящиеся к однородным линейным уравнениям с постоянными коэффициентами при помощи замены независимой переменной.
, приводящиеся к однородным линейным уравнениям с постоянными коэффициентами при помощи замены независимой переменной.
53. Найти расстояние между двумя соседними нулями любого (нетождественно равного нулю) решения уравнения 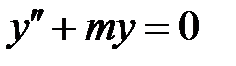 , где
, где 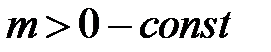 . Сколько нулей может содержаться на отрезке
. Сколько нулей может содержаться на отрезке 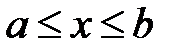 ?
?
54. Доказать, что решение уравнения 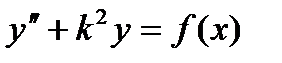 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 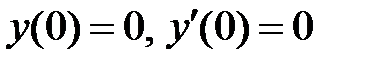 , имеет вид
, имеет вид
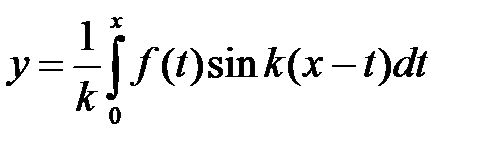 .
.
55. Какие условия достаточно наложить на функцию 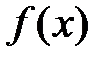 , чтобы все решения уравнения
, чтобы все решения уравнения 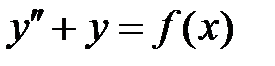 оставались ограниченными при
оставались ограниченными при 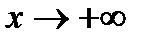 ?
?
56. При каких 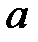 и
и 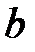 все решения уравнения
все решения уравнения 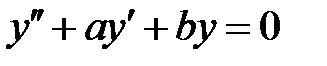
а) ограничены на всей числовой оси 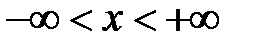 ;
;
б) стремятся к нулю при 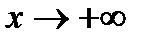 ;
;
в) удовлетворяют соотношению 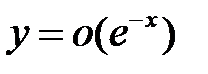 при
при 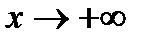 ?
?
57. При каких действительных 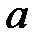 и
и 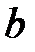 каждое решение уравнения
каждое решение уравнения 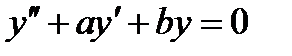 обращается в нуль на бесконечном множестве точек
обращается в нуль на бесконечном множестве точек 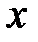 ?
?
58. Найти периодическое решение уравнения 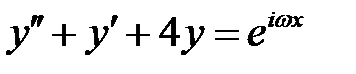 .
.
59. Дано уравнение 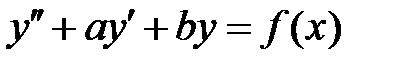 , причем
, причем 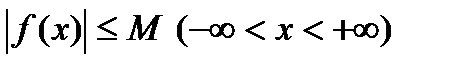 , а корни характеристического уравнения удовлетворяют неравенству
, а корни характеристического уравнения удовлетворяют неравенству 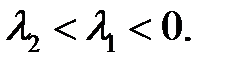 Найти решение, ограниченное при
Найти решение, ограниченное при 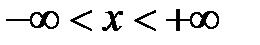 . Показать, что
. Показать, что
а) все остальные решения при 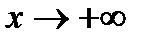 неограниченно приближаются к этому решению;
неограниченно приближаются к этому решению;
б) если 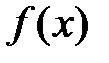 - периодическая функция, то решение также периодическое.
- периодическая функция, то решение также периодическое.
60. Найти общее решение уравнения
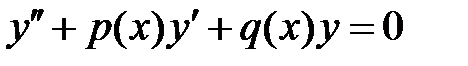 (*)
(*)
с непрерывными коэффициентами на 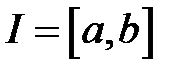 , если известно его частное решение
, если известно его частное решение 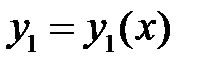 .
.
61. Может ли уравнение (*) иметь решения 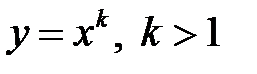 ?
?
62. Пусть 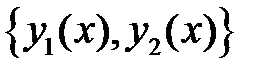 - фундаментальная система решений уравнения (*). Выразить коэффициенты
- фундаментальная система решений уравнения (*). Выразить коэффициенты 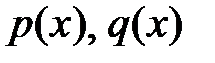 через
через 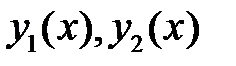 .
.
63. Доказать, что в случае 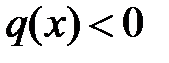 решения уравнения (*) не могут иметь положительных максимумов.
решения уравнения (*) не могут иметь положительных максимумов.
64. Доказать, что два решения уравнения (*), имеющие максимум при одном и том же значении 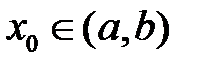 , линейно зависимы на
, линейно зависимы на 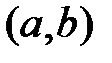 .
.
65. Представить в канонической форме следующие уравнения второго порядка:
а) 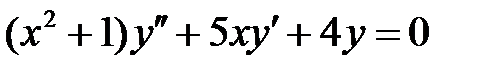 ; б)
; б) 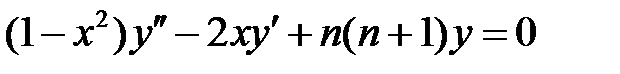 .
.
66. Следующие уравнения привести к самосопряженной форме:
а) 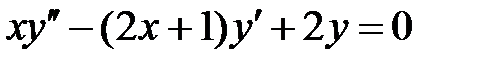 ; б)
; б) 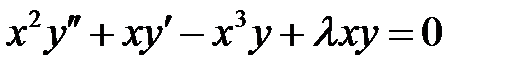 .
.
67. При каких 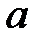 краевая задача
краевая задача 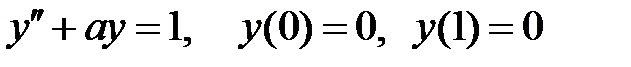 не имеет решений?
не имеет решений?
68. Если в линейном дифференциальном уравнении 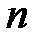 -го порядка сделать замену
-го порядка сделать замену 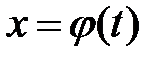 такую, что выполняются условия
такую, что выполняются условия 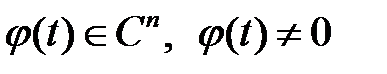 , то будет ли преобразованное уравнение линейным?
, то будет ли преобразованное уравнение линейным?
69. Построить особые кривые и особые решения уравнений:
а) 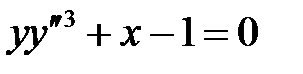 ; б)
; б) 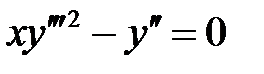 .
.
70. Решить следующие задачи Коши:
а) 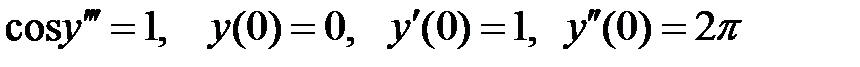 ;
;
б) 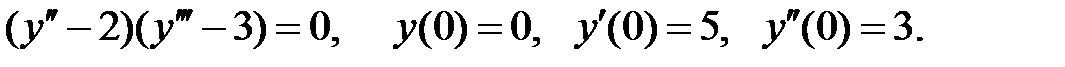
71. Можно ли задачу Коши для линейного обыкновенного дифференциального уравнения 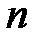 -го порядка
-го порядка
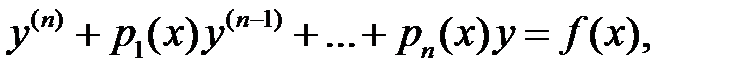
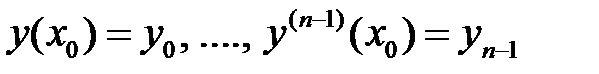
преобразовать эквивалентным образом в задачу Коши с нулевыми начальными значениями?
72. Можно ли линейное дифференциальное уравнение второго порядка
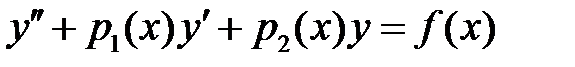
преобразовать к эквивалентному уравнению, не содержащему первой производной?
73. Если в линейном дифференциальном уравнении второго порядка
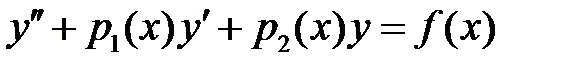 ,
,
положить 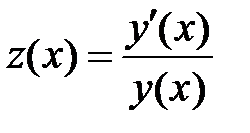 , то какому дифференциальному уравнению будет удовлетворять функция
, то какому дифференциальному уравнению будет удовлетворять функция  ?
?
74. В каком случае решения задач Коши
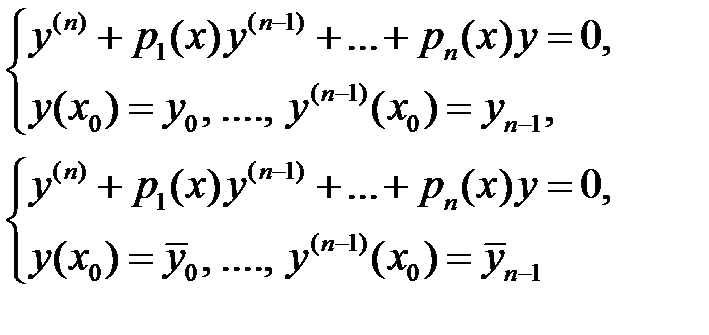
будут линейно независимыми функциями?
75. При выполнении каких условий краевая задача
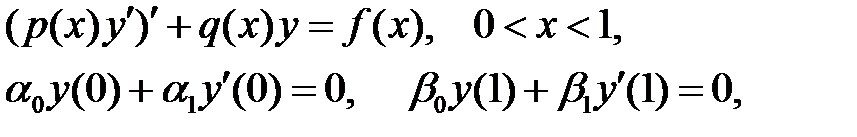
будет иметь единственное решение?
76. Будут ли ортогональными в пространстве 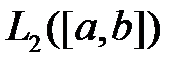 , и при каких
, и при каких 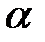 и
и 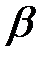 , собственные функции задачи
, собственные функции задачи
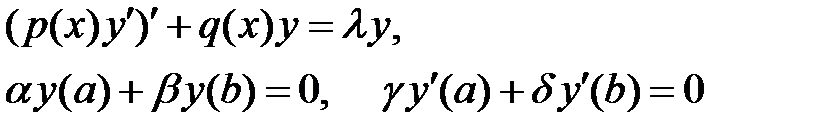
(здесь 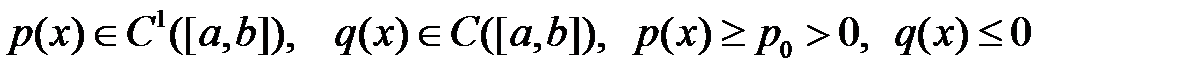 при
при 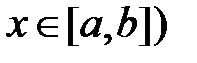 ?
?
77. Какие линейно независимые решения имеет уравнение Бесселя?
78. Какие линейно независимые решения имеет гипергеометрическое уравнение?
79. Можно ли преобразовать уравнение Лежандра к гипергеометрическому уравнению?
80. Будет ли корректной на интервале 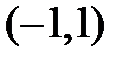 задача Коши для уравнения Лежандра при задании начальных условий при
задача Коши для уравнения Лежандра при задании начальных условий при 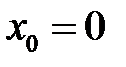 ?
?
81. В каком случае всякое решение дифференциального уравнения присоединенных функций выражается лишь через одну присоединенную функцию Лежандра?
ГЛАВА 6








