Задание № 18. Принцип суперпозиции
Решить уравнения.
Составить линейное однородное уравнение по фундаментальной системе решений (ФСР).
Решить линейное неоднородное уравнение, используя принцип суперпозиции для нахождения частного решения.
Определить вид частного решения (не находя числовые значения коэффициентов).
Применяя различные методы, решить уравнение.
1. 
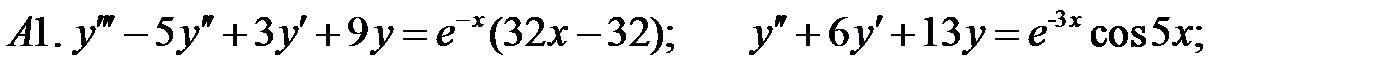
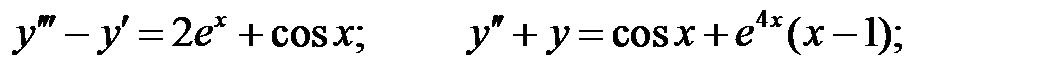
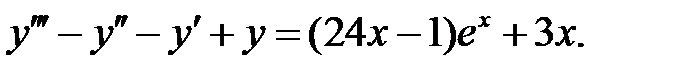
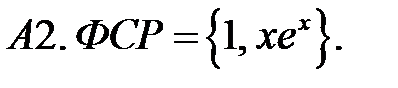
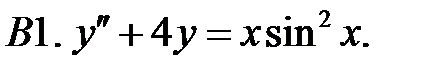
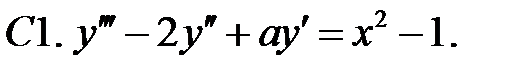
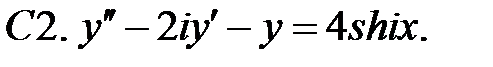
2. 
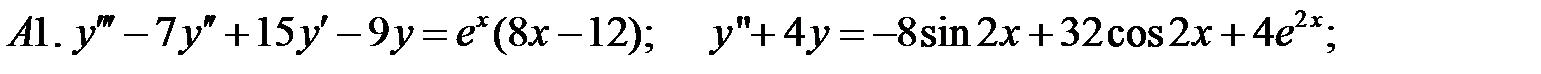
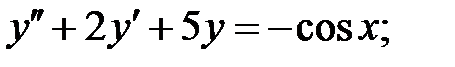
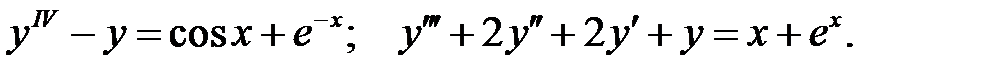
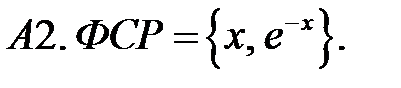
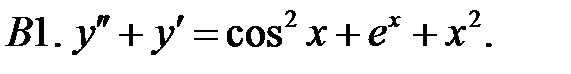
C1.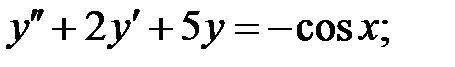 
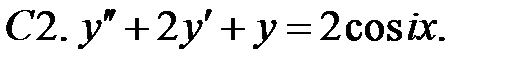
3. 
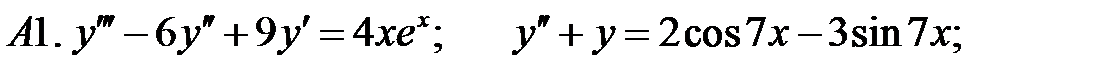
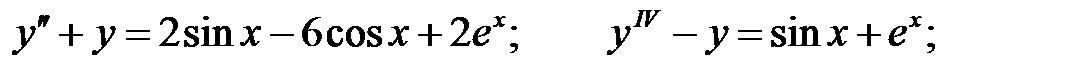
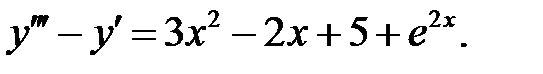
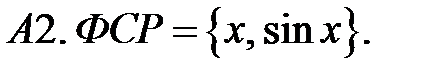
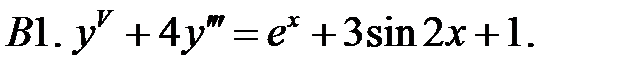
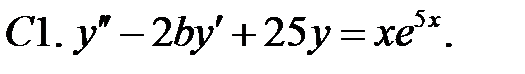
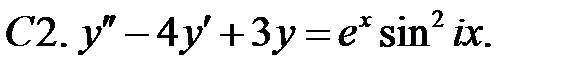
4. 
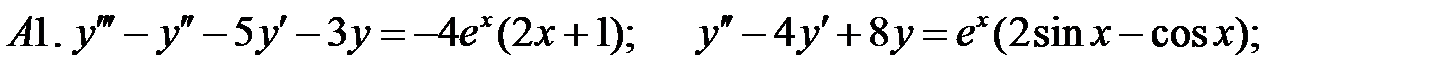
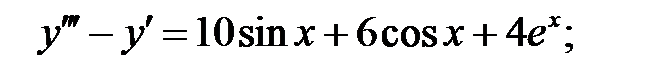
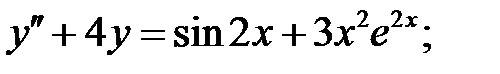
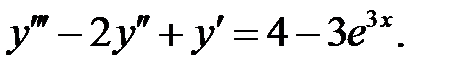
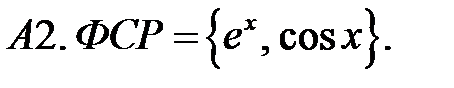
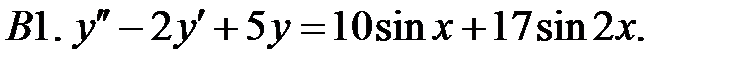
C1.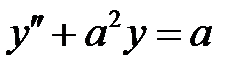 
. 
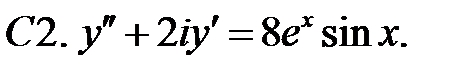
5. 
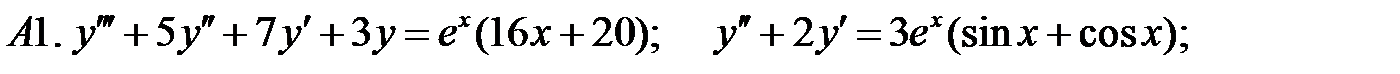
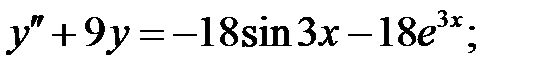
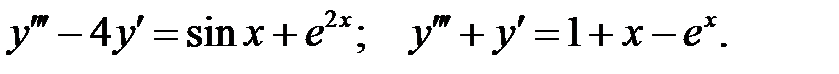
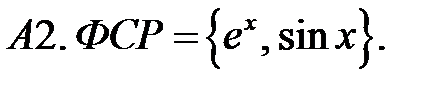
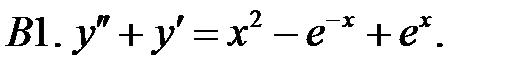
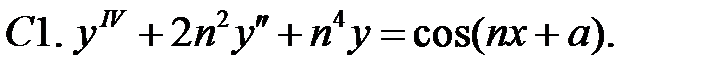
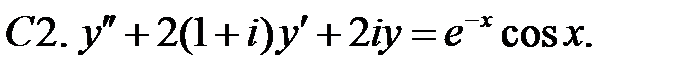
6. 
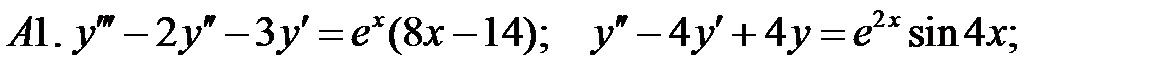
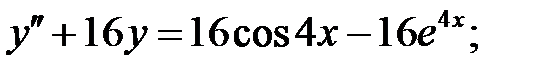
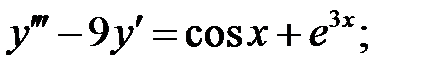
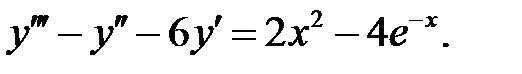
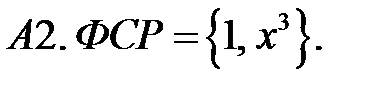
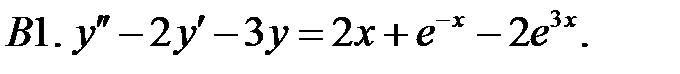
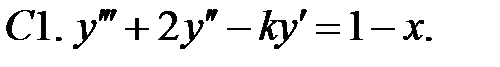
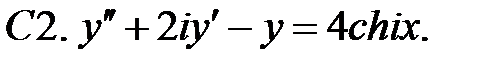
7. 
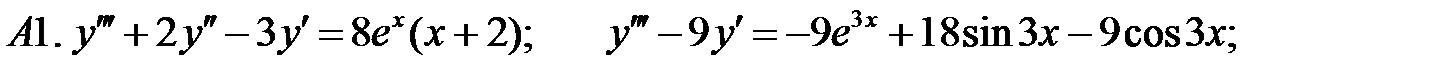
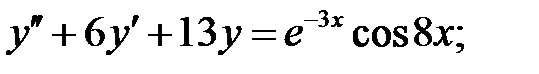
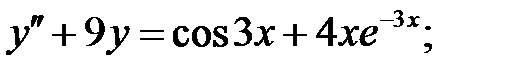
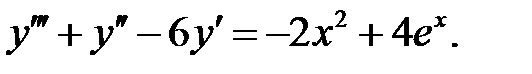
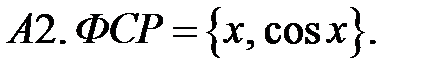
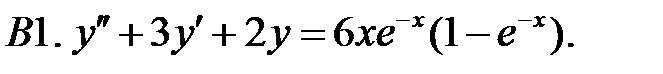
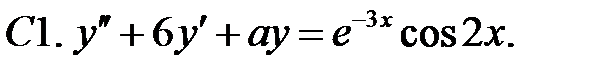
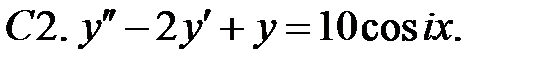
8. 
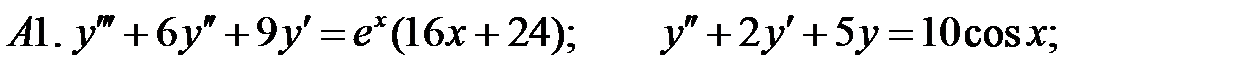
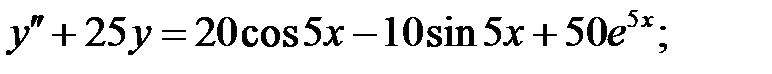
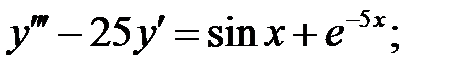
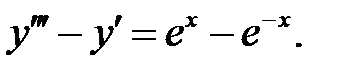
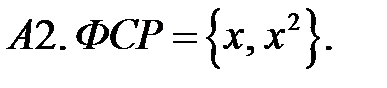
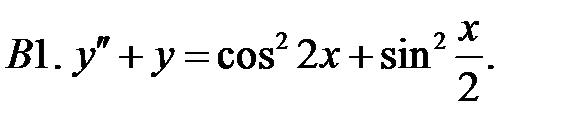
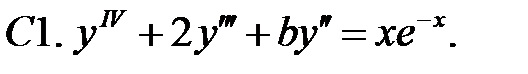
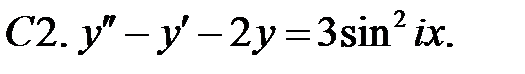
9. 
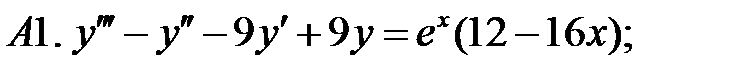
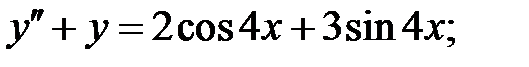
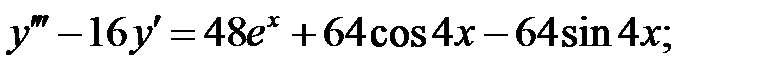
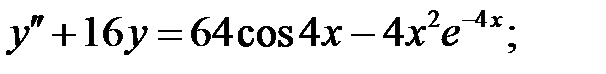
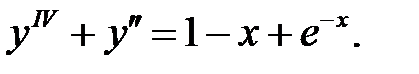
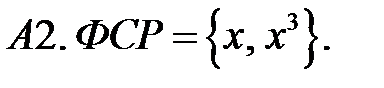
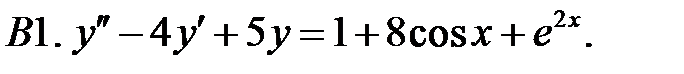
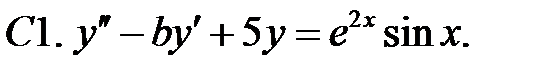
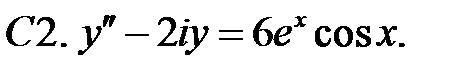
10. 
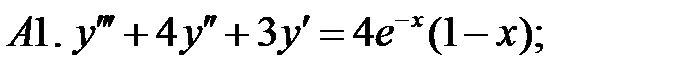
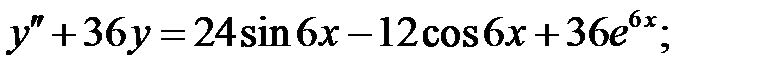
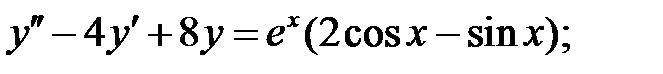
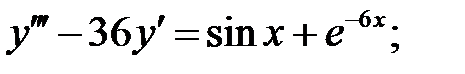
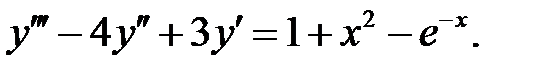
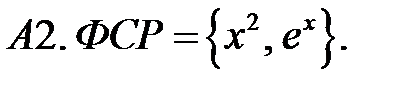
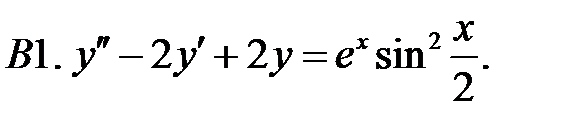
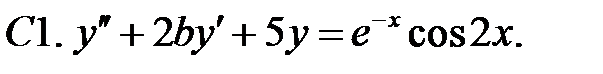
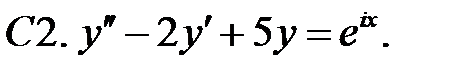
11. 
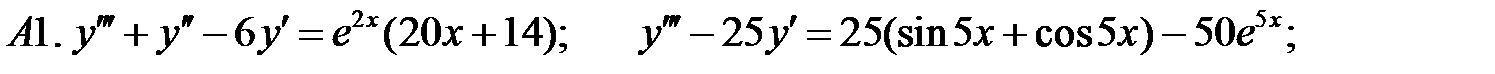
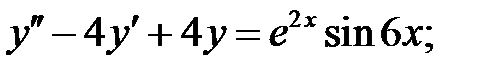
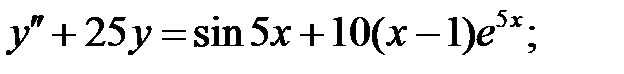
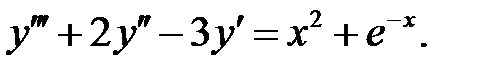
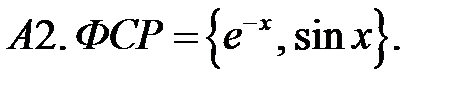
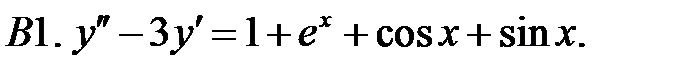
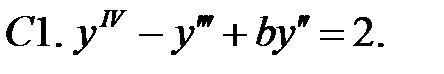
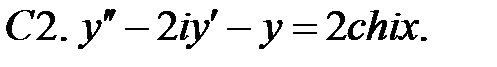
12. 
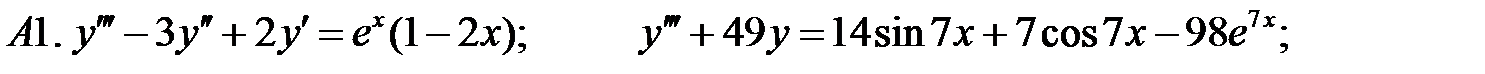
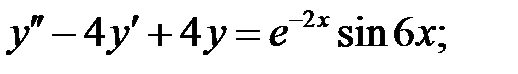
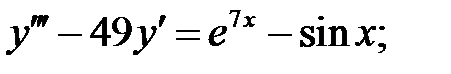
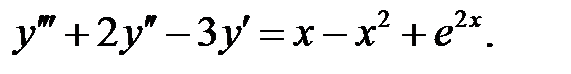
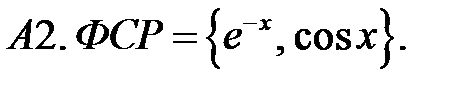
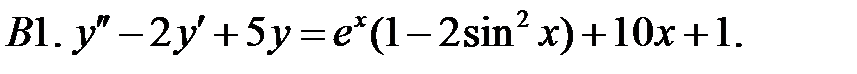
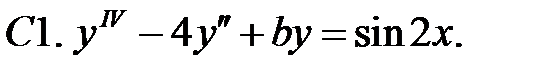
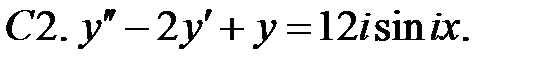
13. 
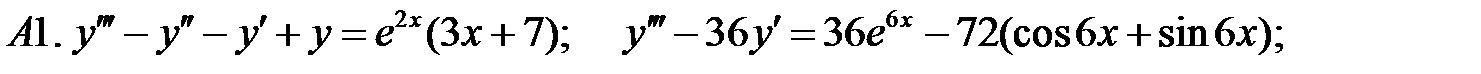
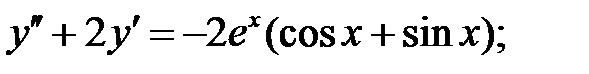
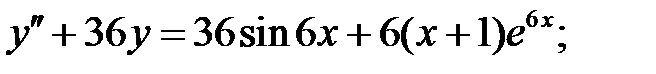
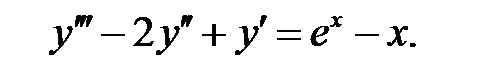
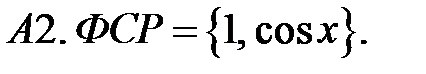
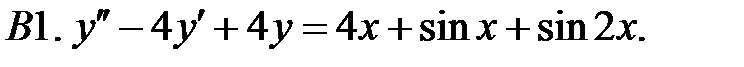
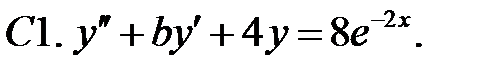
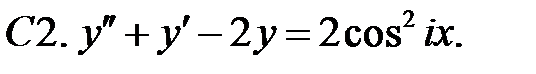
14. 
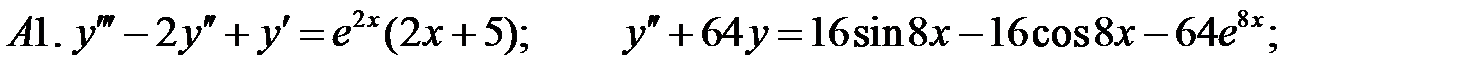
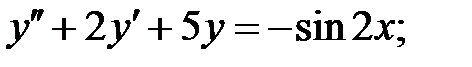
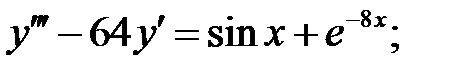
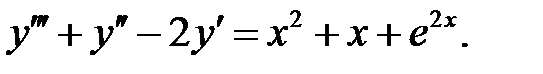
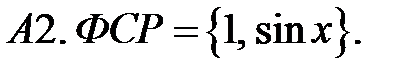
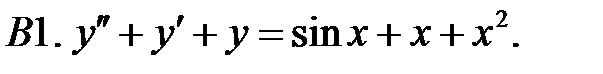
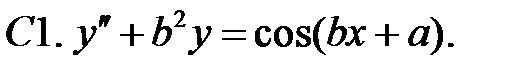
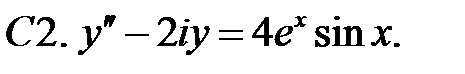
15. 
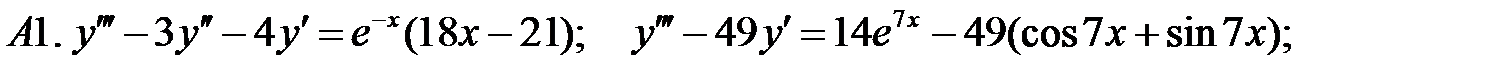
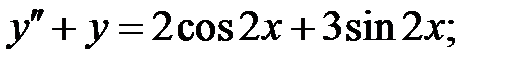
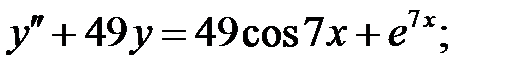
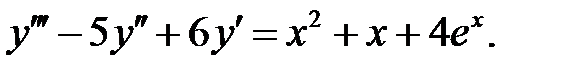
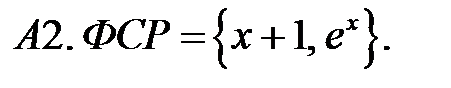
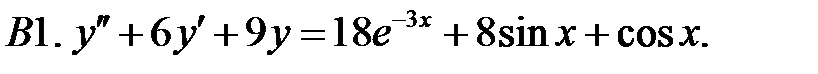
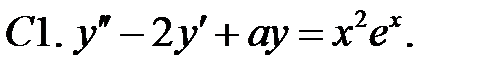
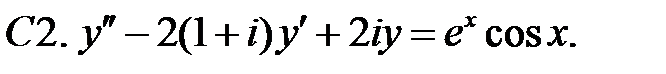
16. 
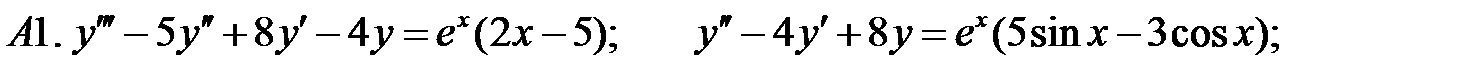
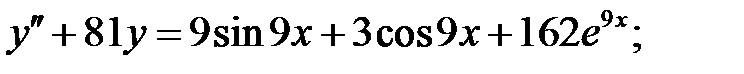
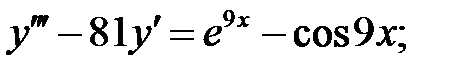
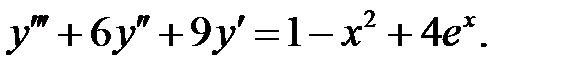
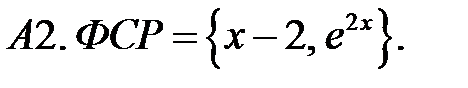
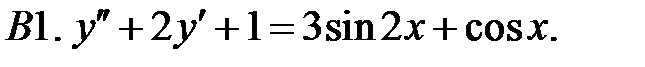
C1.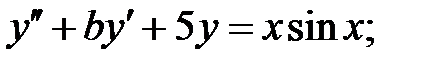 
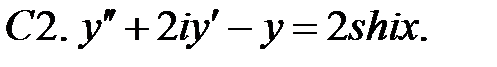
17. 
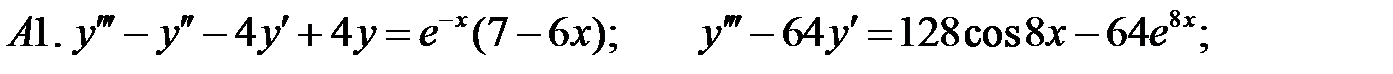
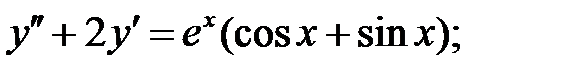
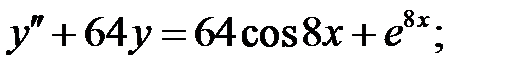
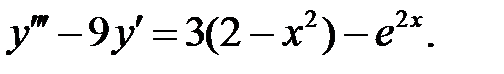
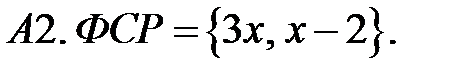
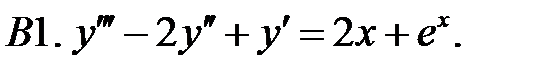
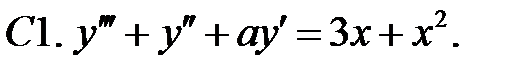
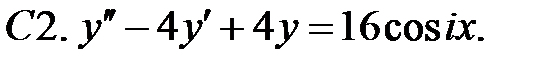
18. 
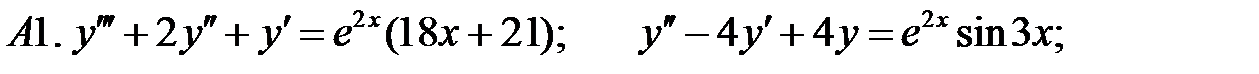
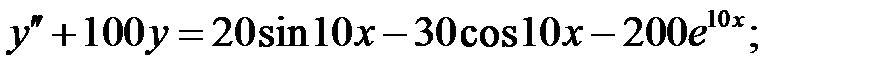
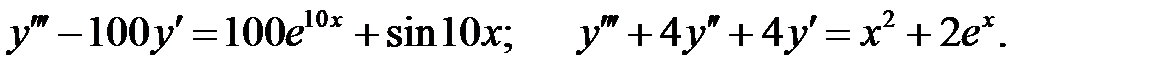
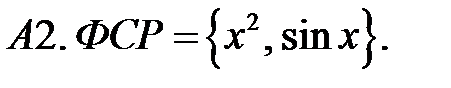
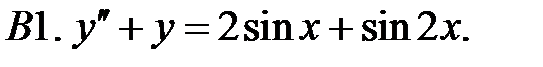
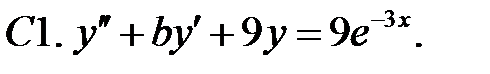
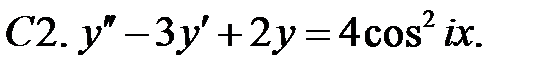
19. 
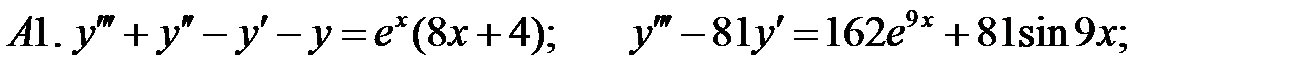
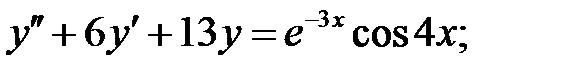
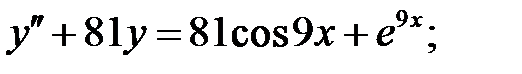
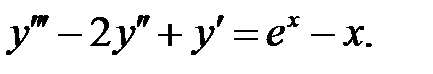
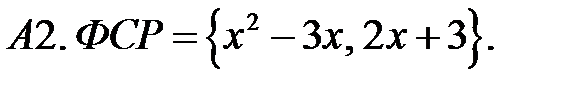
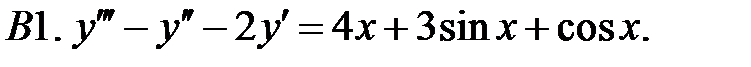
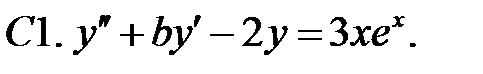
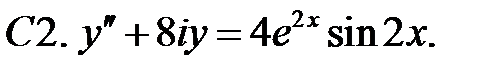
20. 
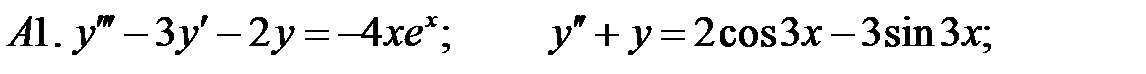
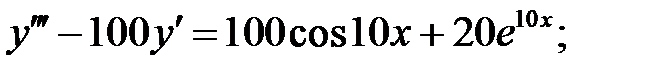
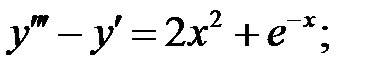
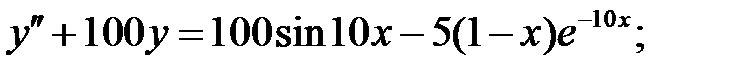
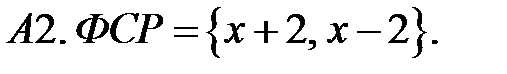
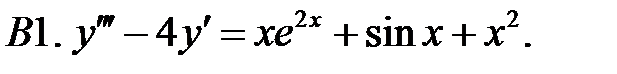
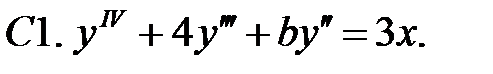
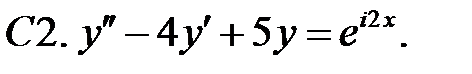
21. 
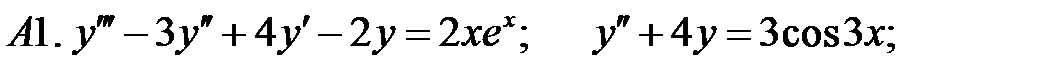
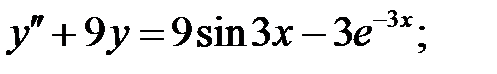
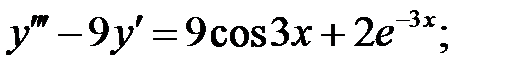
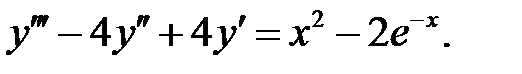
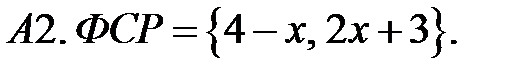
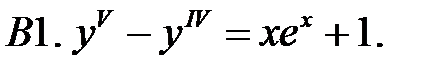
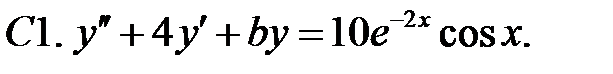
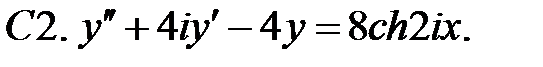
22. 
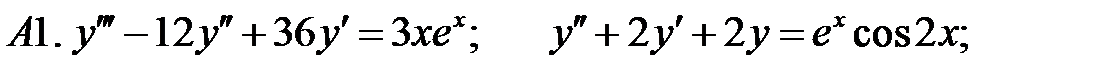
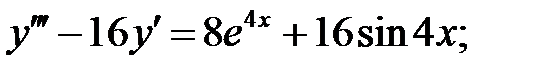
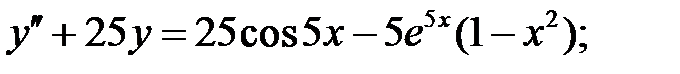
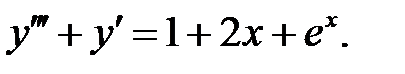
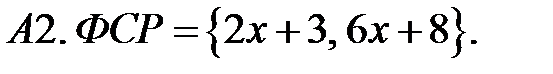
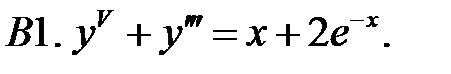
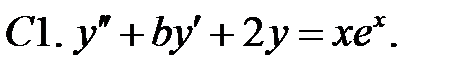
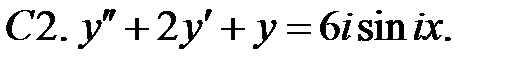
23. 
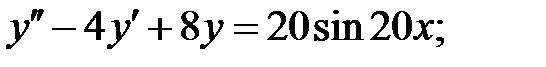
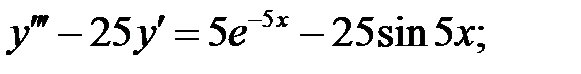
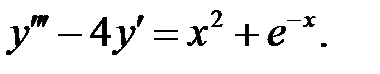
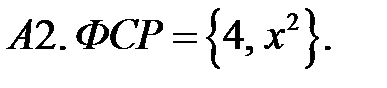
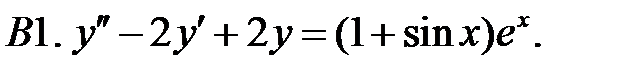
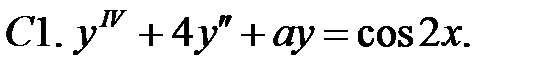
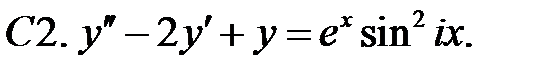
24. 
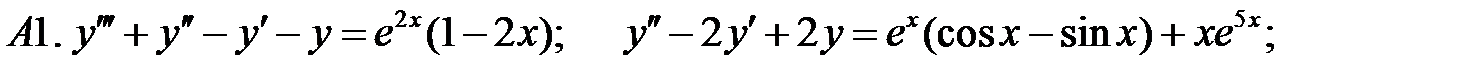
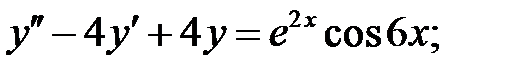
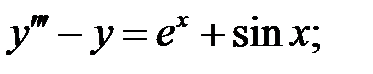
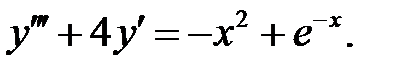
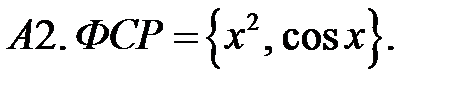
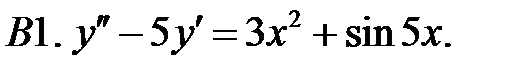
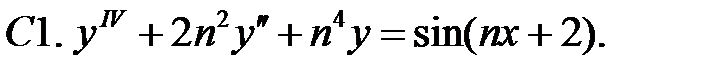
С2.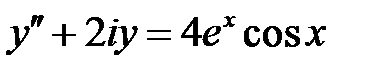 
.
25. 
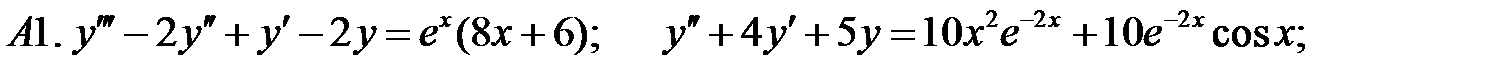
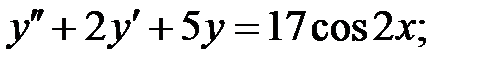
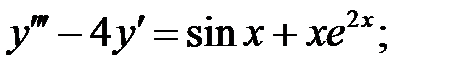
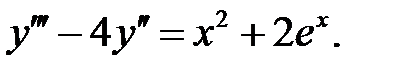
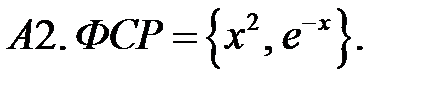
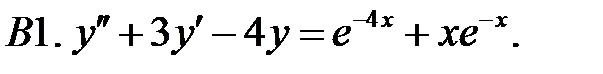
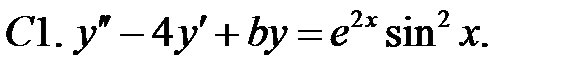
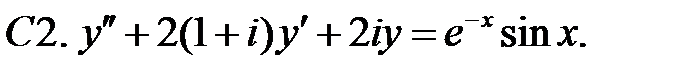
Задание № 19. Метод Лагранжа
Найти общие решения линейных неоднородных уравнений, применяя метод Лагранжа для нахождения их частных решений.
Решить задачу Коши.
Определить вид частного решения (числовые значения коэффициентов не находить).
Найти общее решение уравнения
. 
.
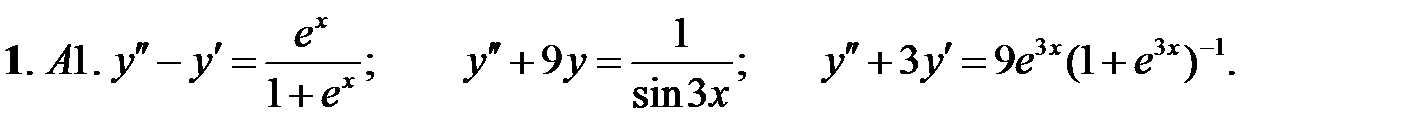
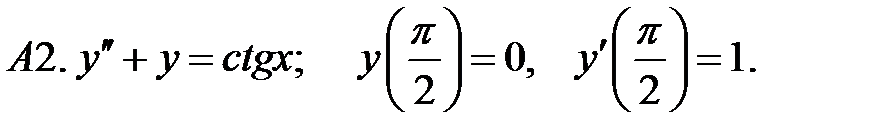
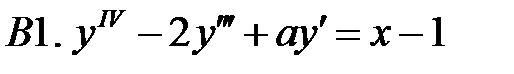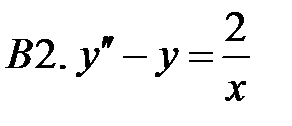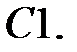Дифференциальное уравнение 
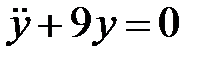описывает свободные вертикальные колебания материальной точки. Определить угловую частоту колебаний.
. 
.
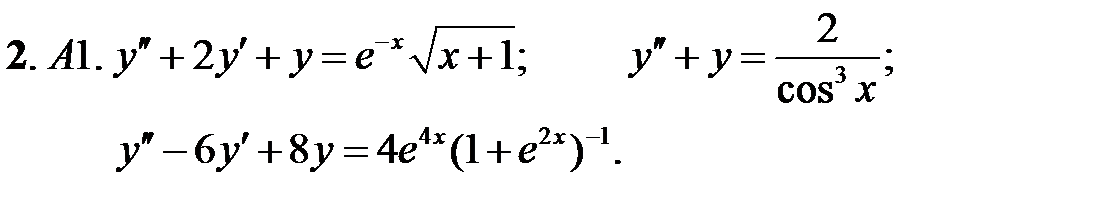
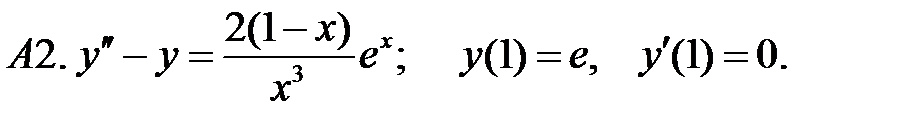
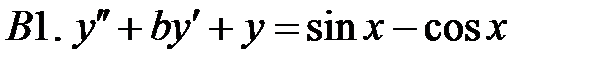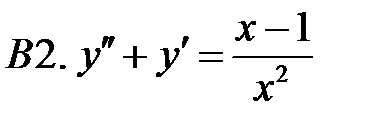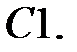Колебание материальной точки задано уравнением 
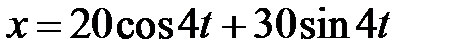, где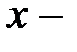 
в см. Определить амплитуду колебаний в см.
. 
.
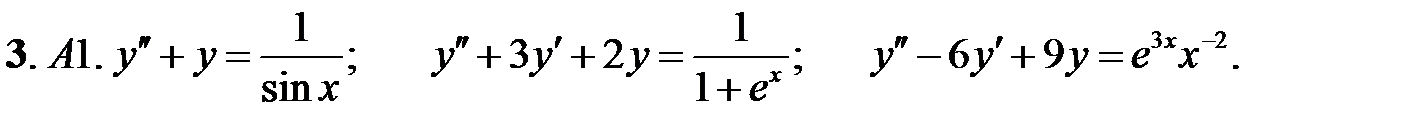
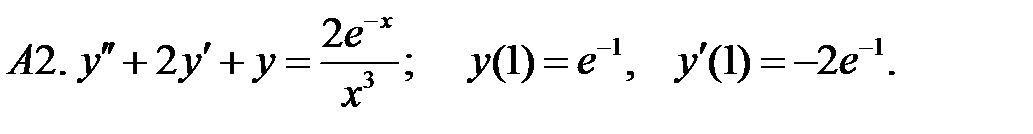
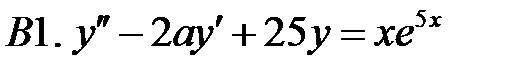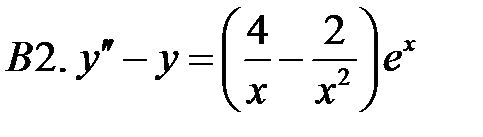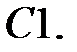Дифференциальное уравнение движения материальной точки имеет вид 
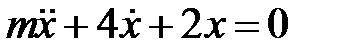. Найти максимальное значение массы точки, при котором движение будет апериодическим.
. 
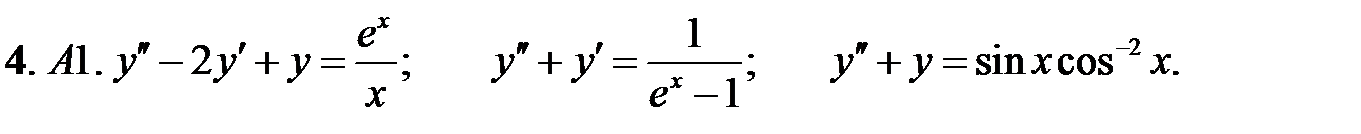
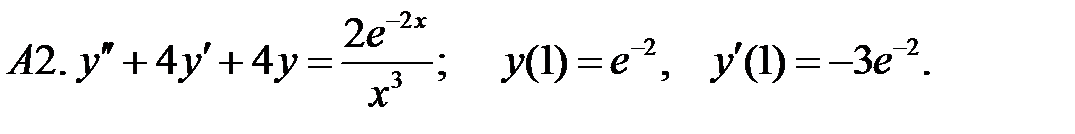
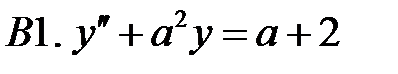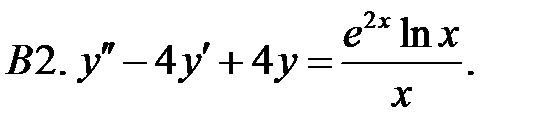
Определить, находится ли материальная точка в колебательном движении, если дифференциальное уравнение движения имеет вид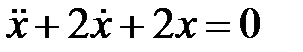 
.
. 
.
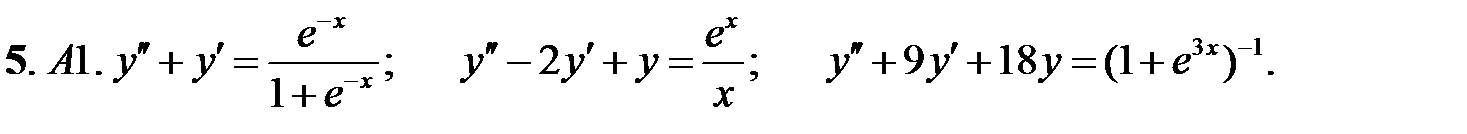
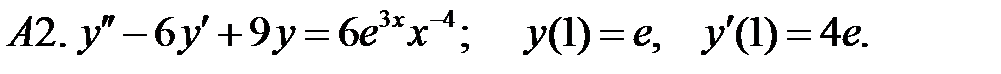
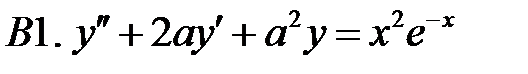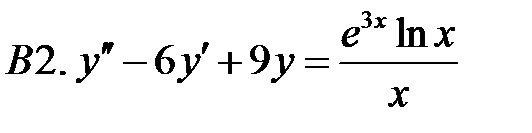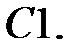Дифференциальное уравнение движения материальной точки имеет вид 
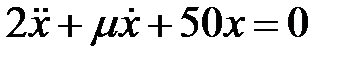. Найти минимальное значение коэффициента 
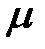сопротивления среды, при котором движение будет апериодическим .
. 
.
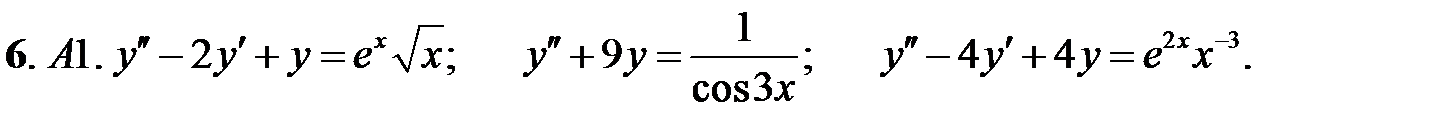
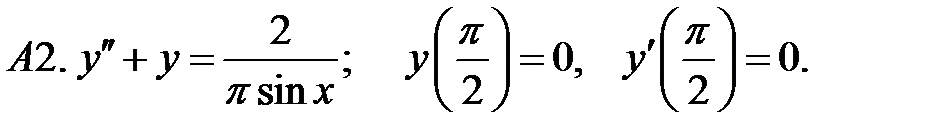
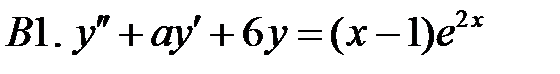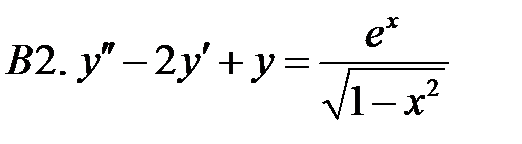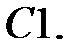Дифференциальное уравнение движения материальной точки имеет вид 
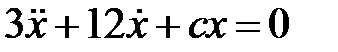. Найти максимальное значение коэффициента жесткости 
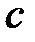, при котором движение будет апериодическим
. 
.
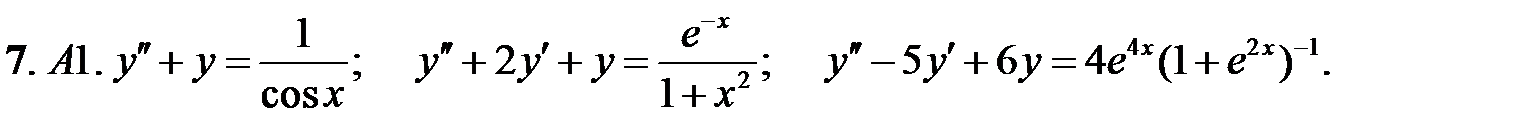
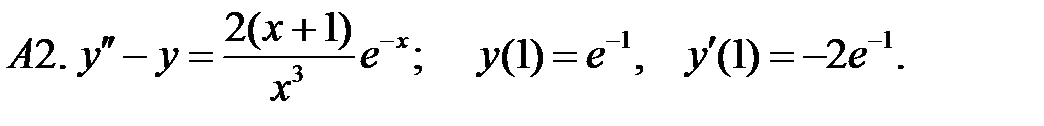
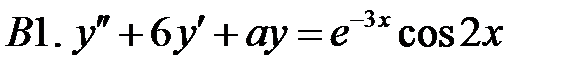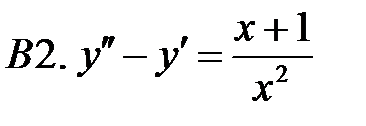Определить, находится ли материальная точка в колебательном движении, если дифференциальное уравнение движения имеет вид 
.
. 
.
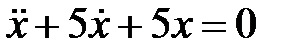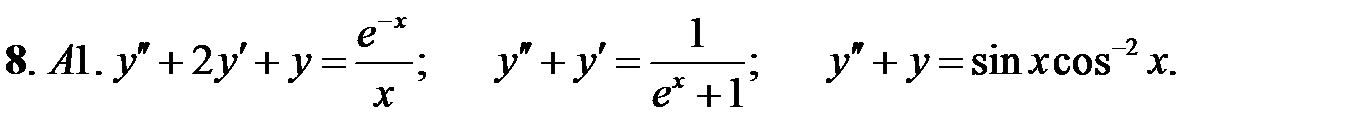
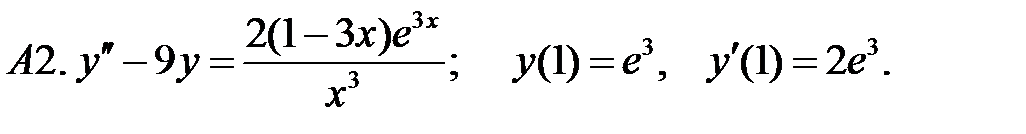
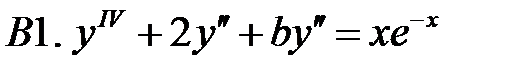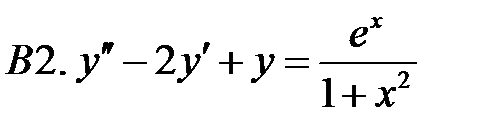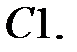Дифференциальное уравнение движения материальной точки имеет вид 
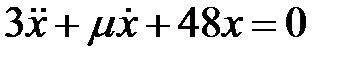. Найти наименьшее значение коэффициента 
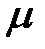сопротивления среды, при котором движение системы будет апериодическим.
. 
.
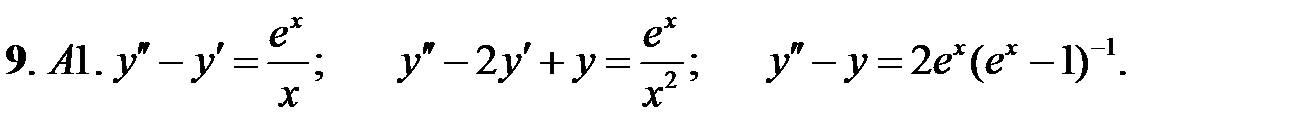
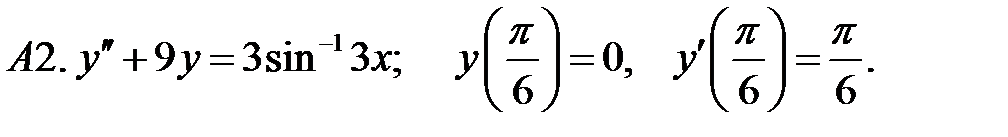
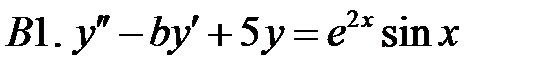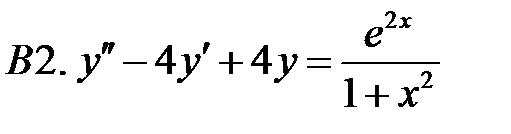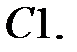Дифференциальное уравнение движения материальной точки имеет вид 
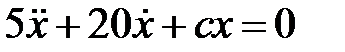. Найти наибольшее значение коэффициента жесткости 
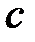, при котором движение точки будет апериодическим.
. 
.
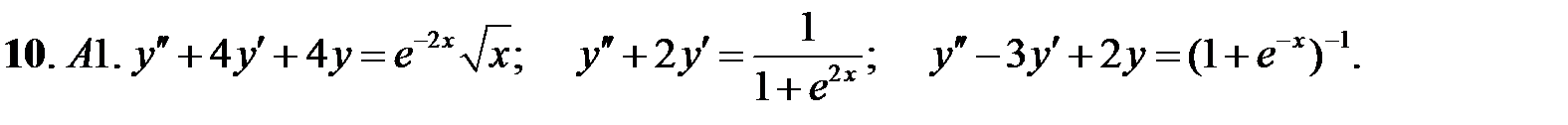
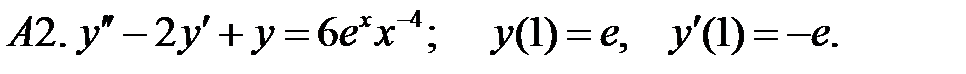
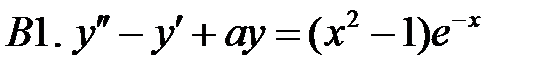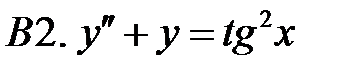Дифференциальное уравнение колебательного движения материальной точки имеет вид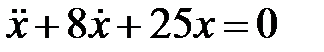 
. Найти угловую частоту затухающих колебаний.
. 
.
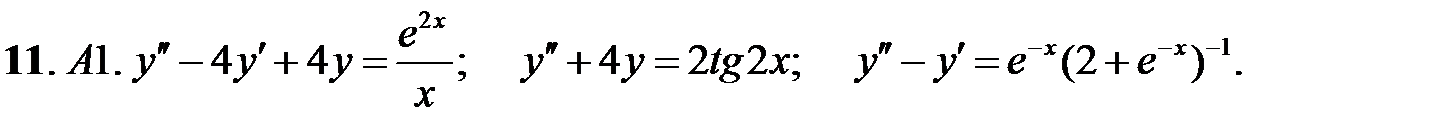
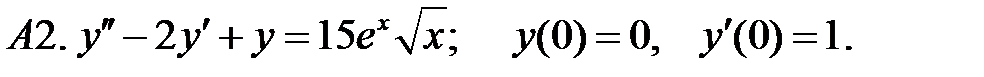
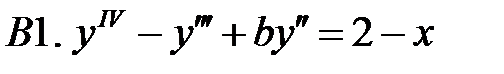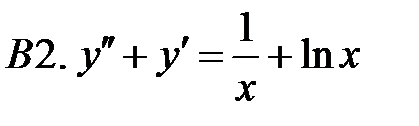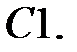Дифференциальное уравнение колебательного движения материальной точки имеет вид 
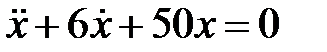. Определить период затухающих колебаний.
. 
.
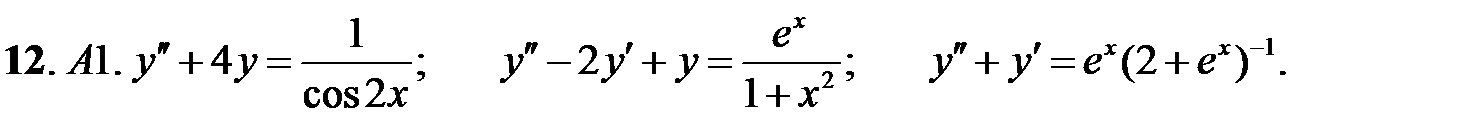
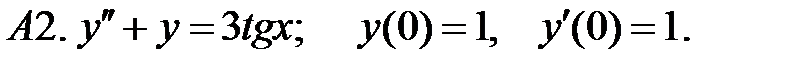
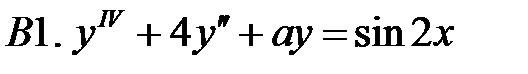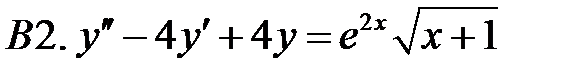Дифференциальное уравнение колебательного движения материальной точки имеет вид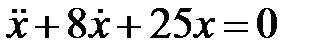 
. Определить период затухающих колебаний.
. 
.
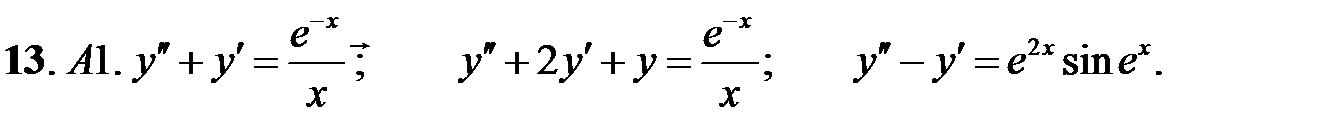
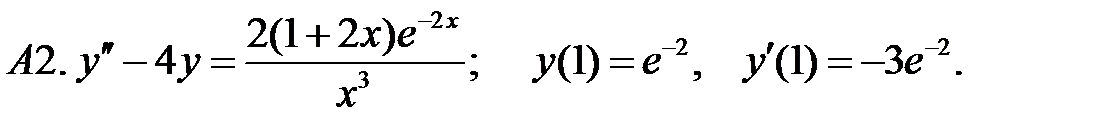
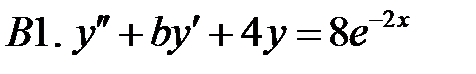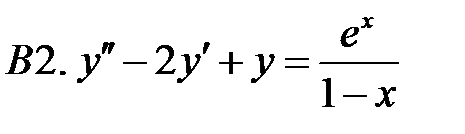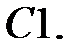Дифференциальное уравнение движения материальной точки имеет вид 
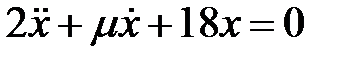. Найти наименьшее значение коэффициента 
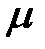сопротивления среды, при котором движение системы будет апериодическим.
. 
.
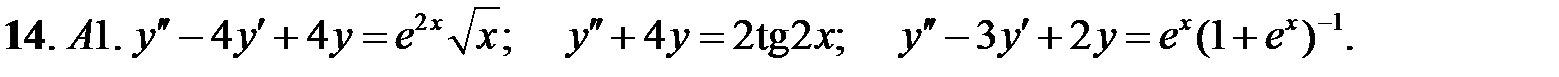
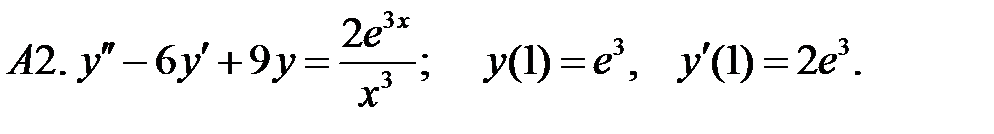
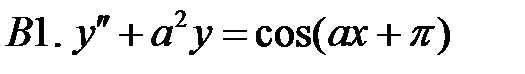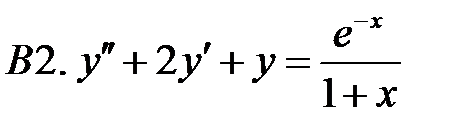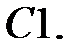Дифференциальное уравнение движения материальной точки имеет вид 
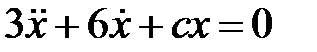. Найти наибольшее значение коэффициента жесткости 
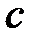, при котором движение точки будет апериодическим.
. 
.
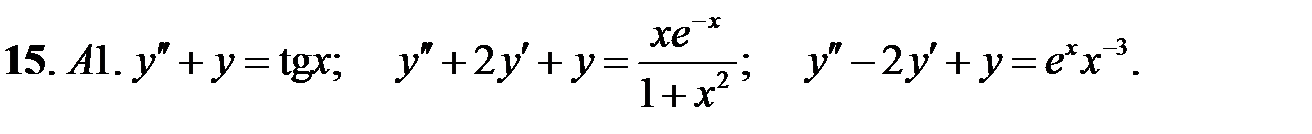
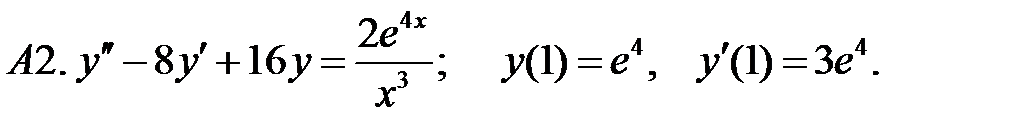
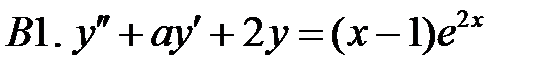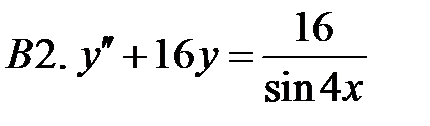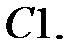Дифференциальное уравнение колебательного движения материальной точки имеет вид 
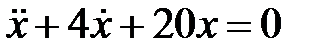. Найти угловую частоту затухающих колебаний.
. 
.
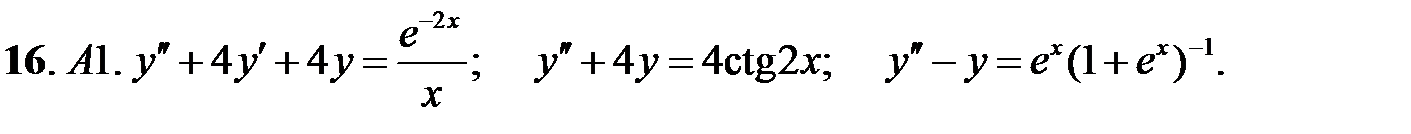
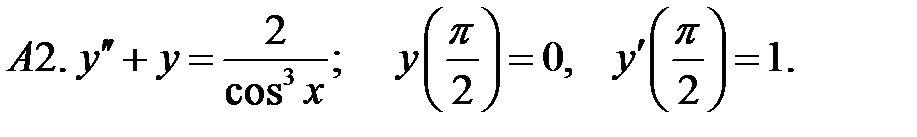
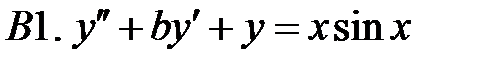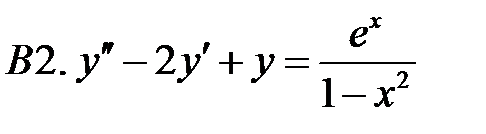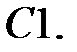Дифференциальное уравнение колебательного движения материальной точки имеет вид 
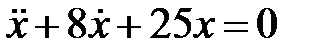. Определить период затухающих колебаний.
. 
.
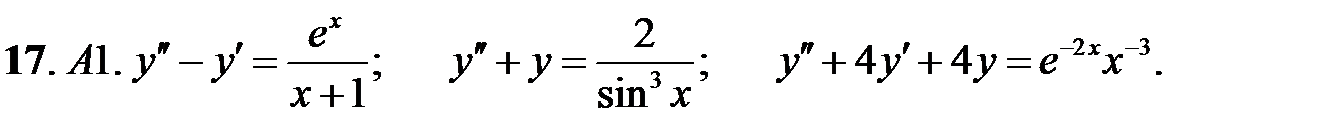
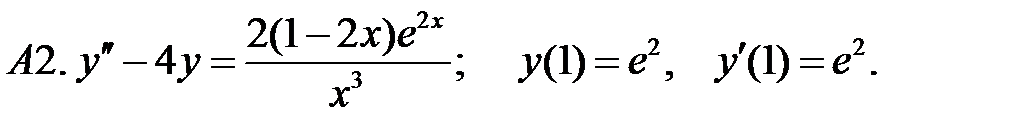
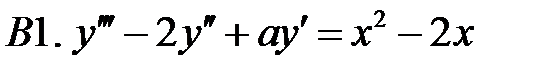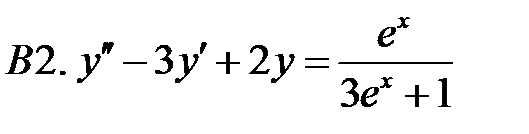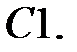Дифференциальное уравнение колебательного движения материальной точки имеет вид 
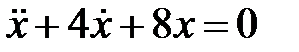. Определить период затухающих колебаний.
. 
.
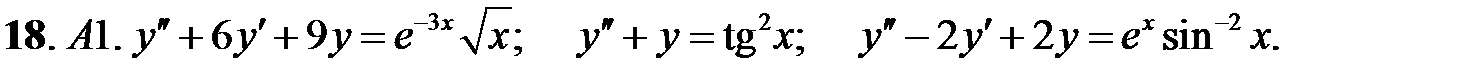
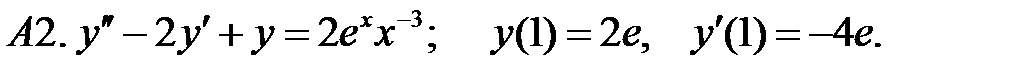
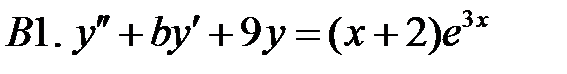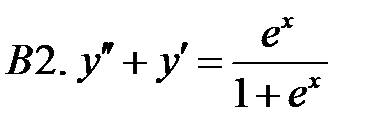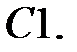Дифференциальное уравнение колебательного движения материальной точки дано в виде 
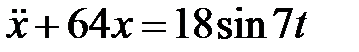. Найти угловую частоту собственных колебаний точки.
. 
.
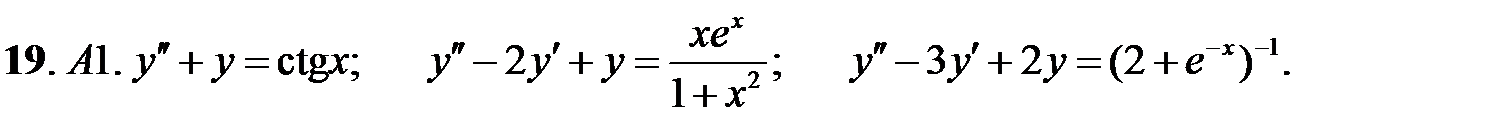
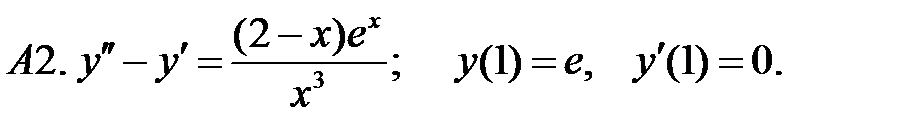
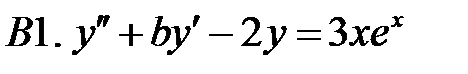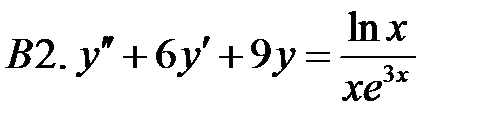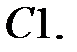Дифференциальное уравнение колебаний материальной точки дано в виде 
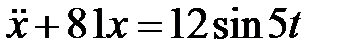. Определить амплитуду вынужденных колебаний.
. 
.
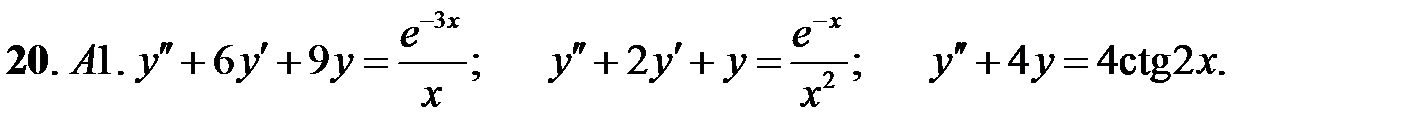
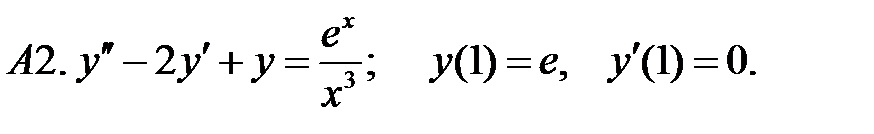
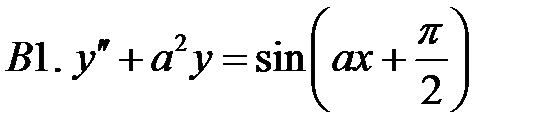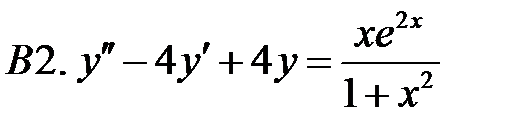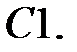Дифференциальное уравнение колебательного движения материальной точки имеет вид 
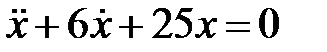. Найти угловую частоту затухающих колебаний.
. 
.
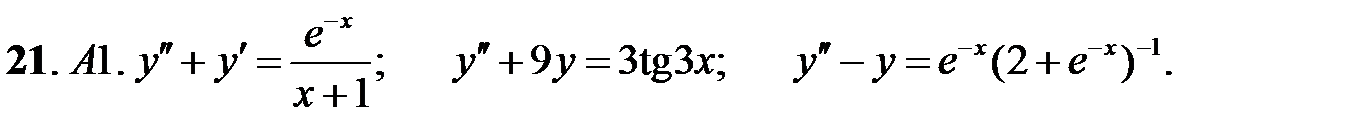
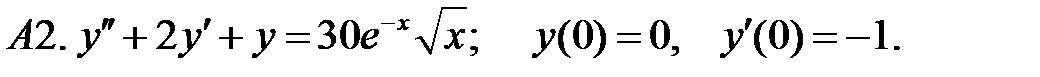
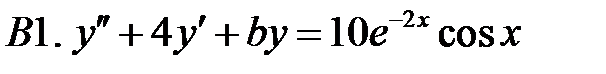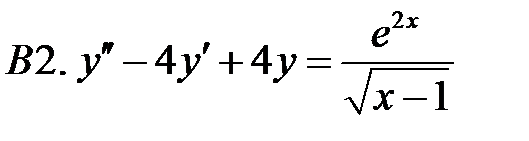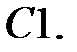Дифференциальное уравнение колебательного движения материальной точки имеет вид 
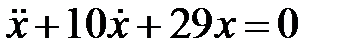. Определить период затухающих колебаний.
. 
.
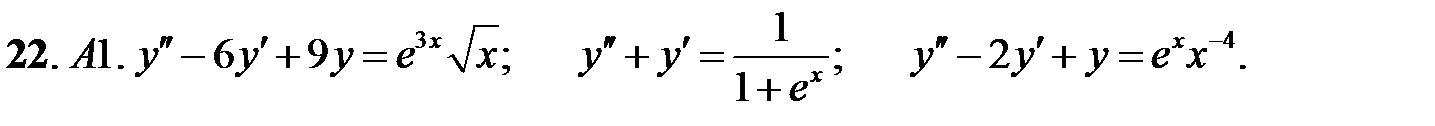
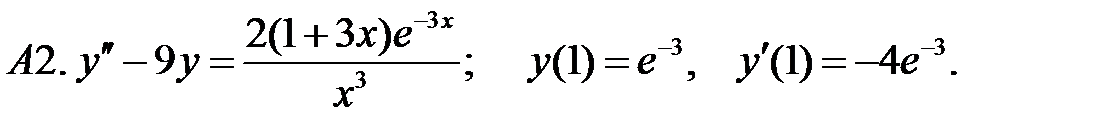
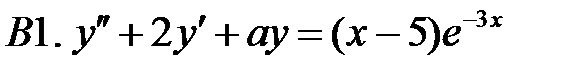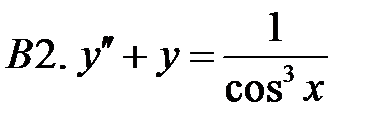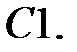Определить амплитуду вынужденных колебаний материальной точки, если дифференциальное уравнение ее движения имеет вид 
.
. 
.
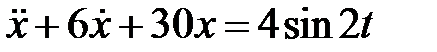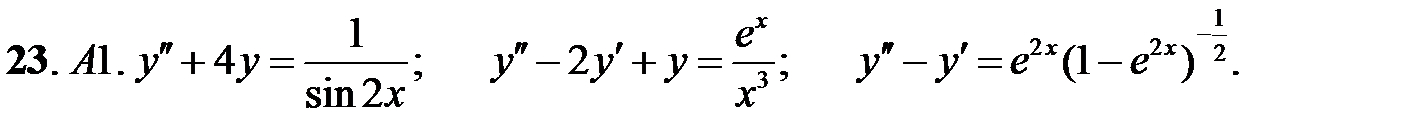
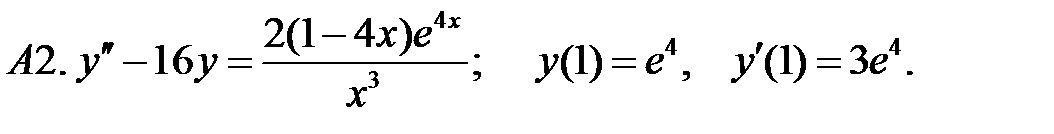
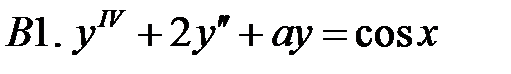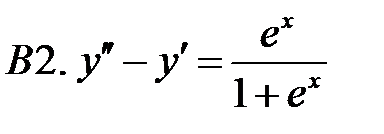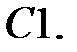Дифференциальное уравнение колебательного движения материальной точки дано в виде 
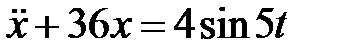. Найти угловую частоту собственных колебаний точки.
. 
.
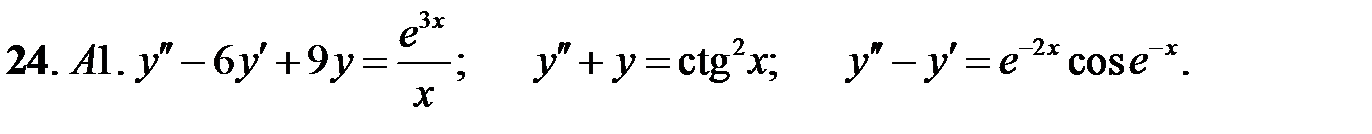
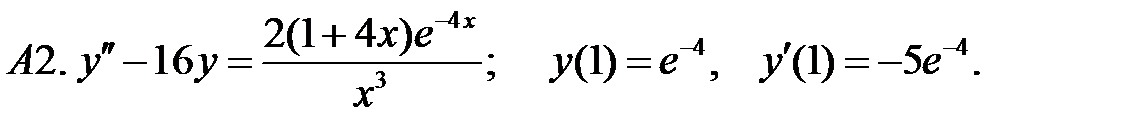
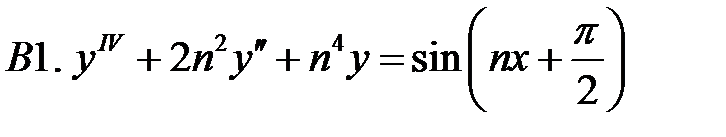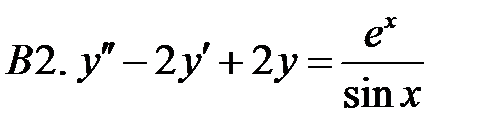Дифференциальное уравнение колебательного движения материальной точки дано в виде 
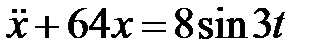. Найти угловую частоту собственных колебаний точки.
. 
.
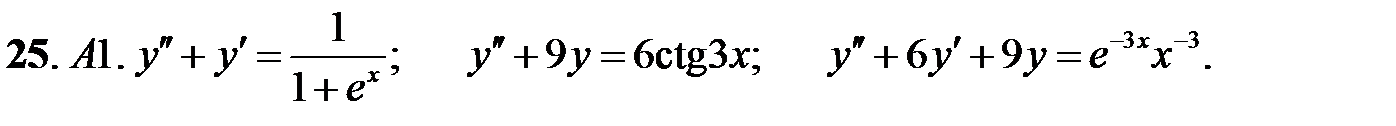
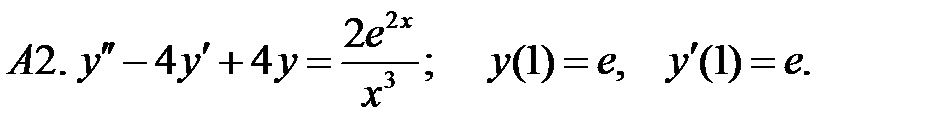
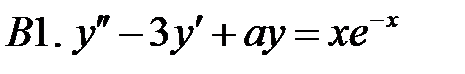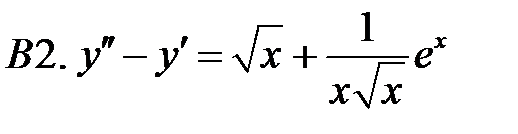Дифференциальное уравнение колебательного движения материальной точки имеет вид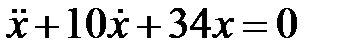 
. Найти угловую частоту затухающих колебаний.