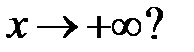Задание № 16. Линейные однородные уравнения
с постоянными коэффициентами
 Найти общие решения линейных однородных уравнений.
Найти общие решения линейных однородных уравнений.
 Найти решение задачи Коши.
Найти решение задачи Коши.
 Найти фундаментальную систему решений уравнения.
Найти фундаментальную систему решений уравнения.
 Найти общее решение линейного однородного уравнения.
Найти общее решение линейного однородного уравнения.
 Составить линейное однородное уравнение с постоянными коэффициентами (возможно наименьшего порядка), имеющее следующие частные решения.
Составить линейное однородное уравнение с постоянными коэффициентами (возможно наименьшего порядка), имеющее следующие частные решения.
 Исследовать, являются ли данные функции линейно независимыми в их области определения.
Исследовать, являются ли данные функции линейно независимыми в их области определения.
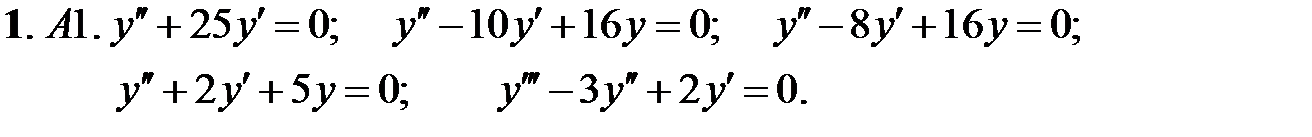
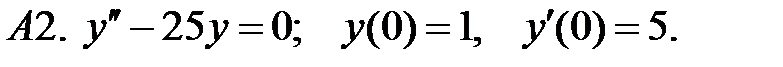
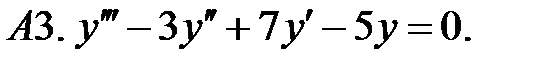
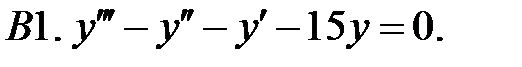
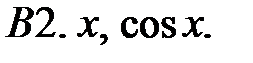
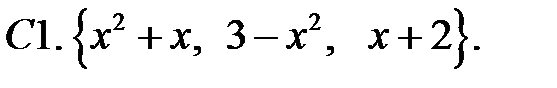
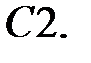 При каких действительных
При каких действительных 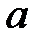 и
и 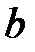 все решения уравнения
все решения уравнения 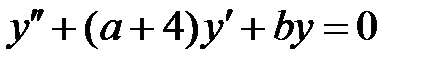 ограничены на всей числовой оси
ограничены на всей числовой оси 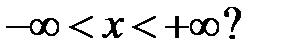
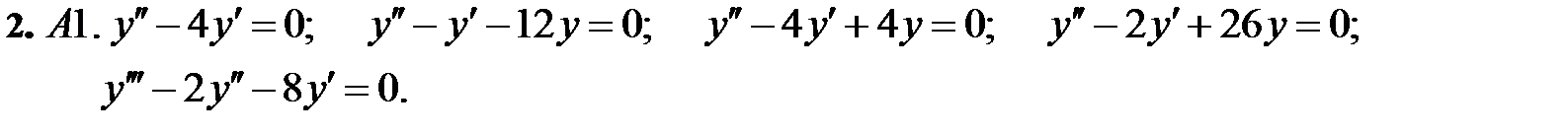
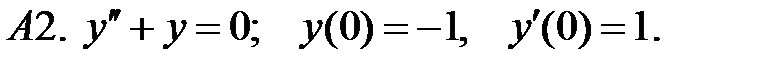
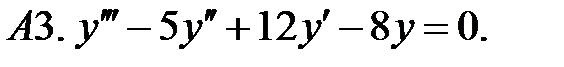
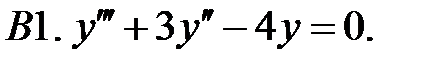
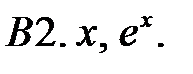
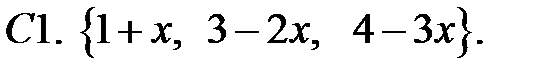
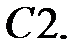 При каких действительных
При каких действительных 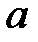 и
и 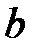 каждое решение уравнения
каждое решение уравнения 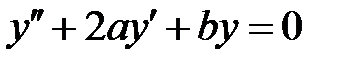 обращается в нуль на бесконечном множестве точек
обращается в нуль на бесконечном множестве точек 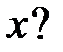
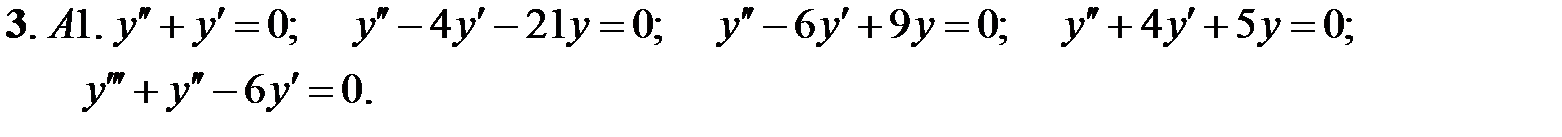
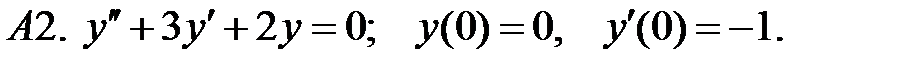
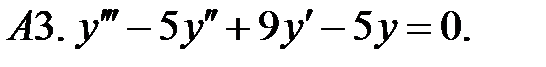
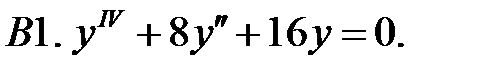
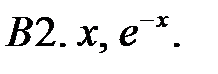
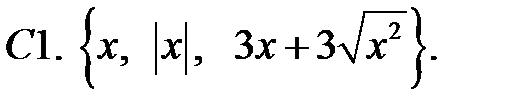
 При каких действительных
При каких действительных 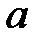 и
и 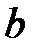 все решения уравнения
все решения уравнения 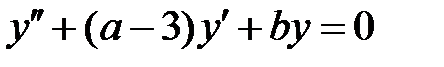 стремятся к нулю при
стремятся к нулю при 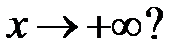
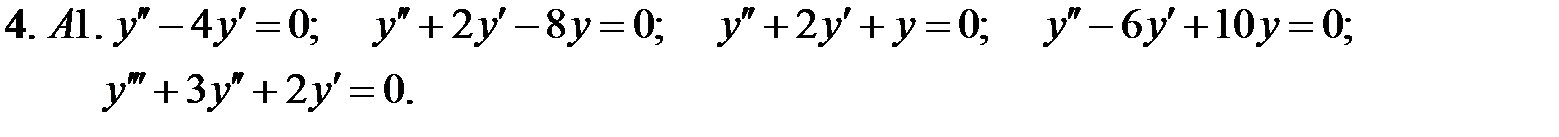
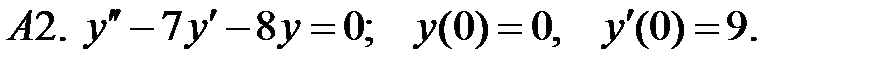
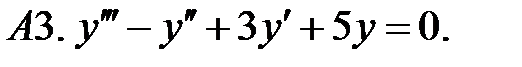
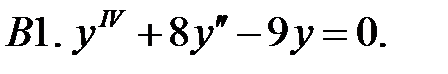
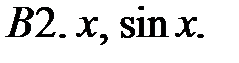
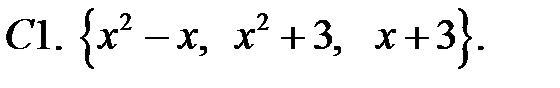
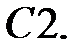 При каких
При каких 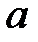 и
и 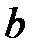 уравнение
уравнение 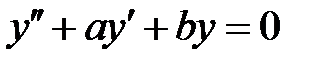 имеет хотя бы одно решение
имеет хотя бы одно решение 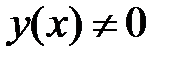 , стремящееся к нулю при
, стремящееся к нулю при 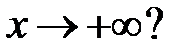
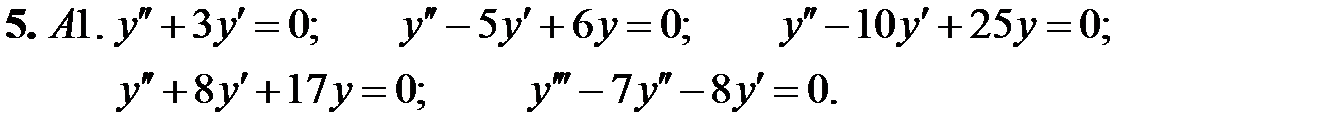
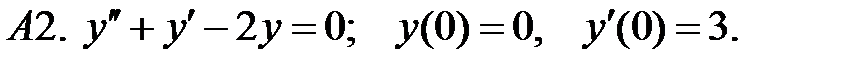
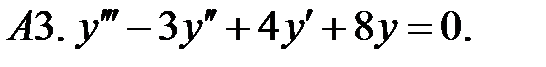
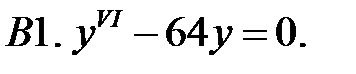
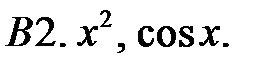
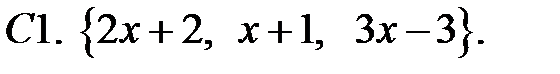
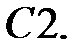 При каких действительных
При каких действительных 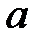 и
и 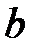 все решения уравнения
все решения уравнения 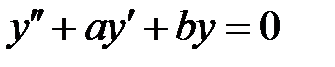 удовлетворяют соотношению
удовлетворяют соотношению 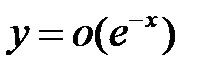 при
при 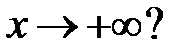
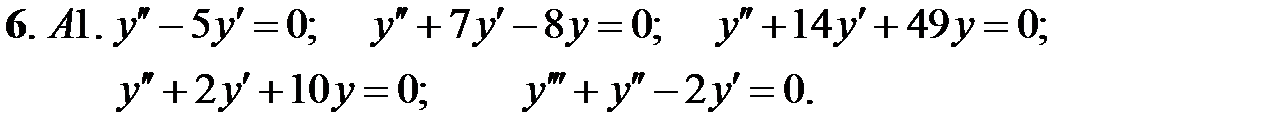
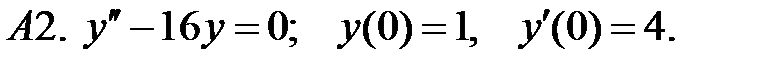
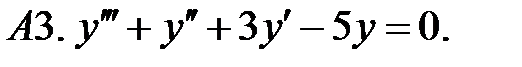
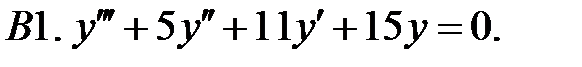
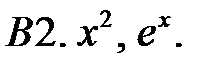
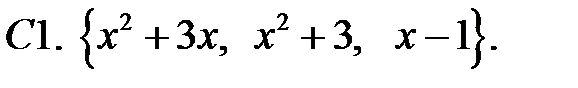
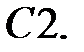 При каких действительных
При каких действительных 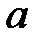 и
и 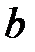 все решения уравнения
все решения уравнения 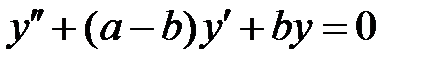 ограничены на всей числовой оси
ограничены на всей числовой оси 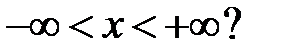
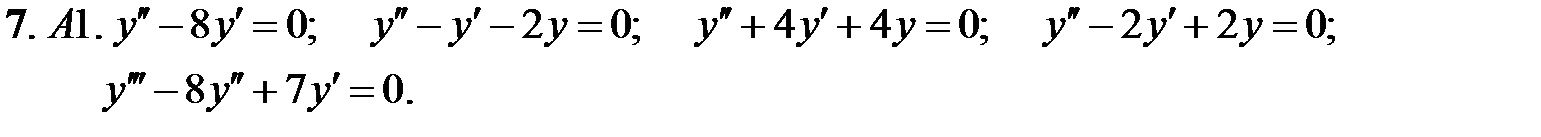
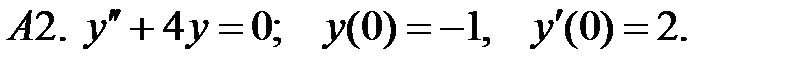
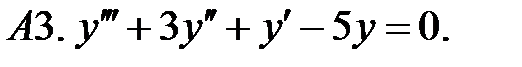
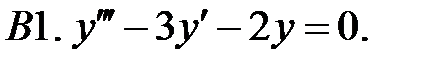
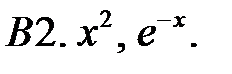
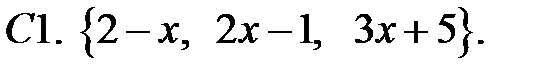
 При каких действительных
При каких действительных 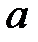 и
и 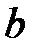 каждое решение уравнения
каждое решение уравнения 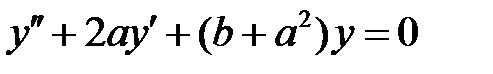 обращается в нуль на бесконечном множестве точек
обращается в нуль на бесконечном множестве точек 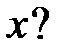
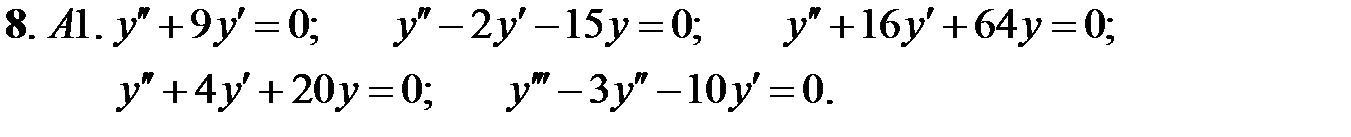
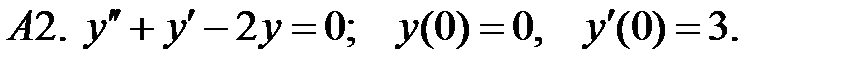
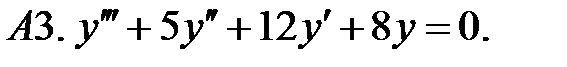
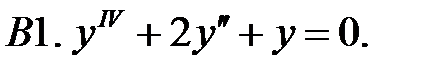
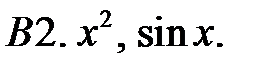
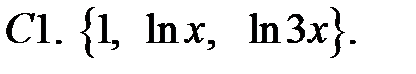
 При каких действительных
При каких действительных 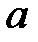 и
и 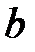 все решения уравнения
все решения уравнения 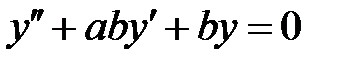 стремятся к нулю при
стремятся к нулю при 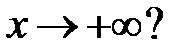
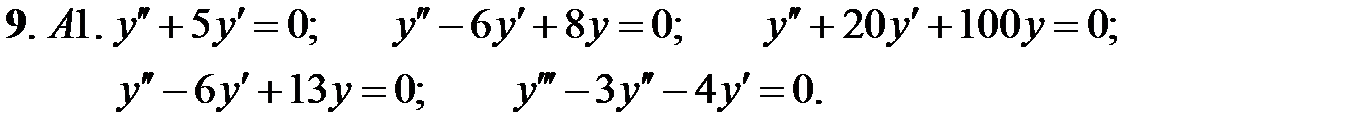
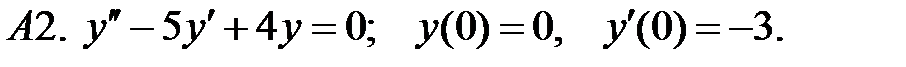
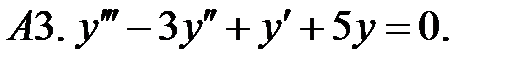
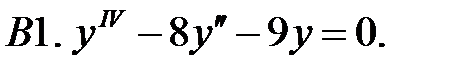
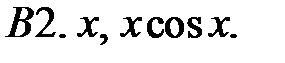
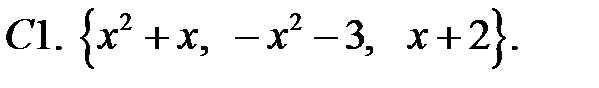
 При каких
При каких 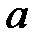 и
и 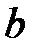 уравнение
уравнение 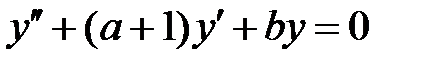 имеет хотя бы одно решение
имеет хотя бы одно решение 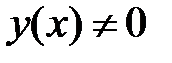 , стремящееся к нулю при
, стремящееся к нулю при 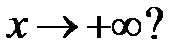
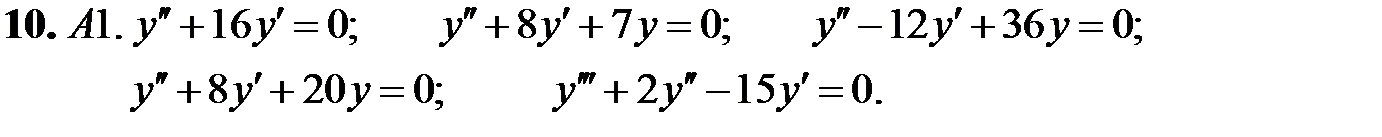
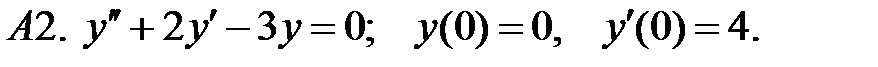
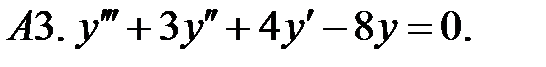
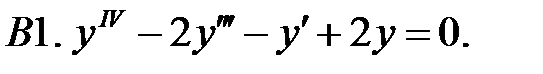
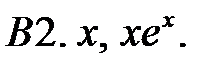
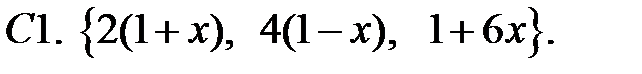
 При каких действительных
При каких действительных 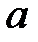 и
и 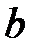 все решения уравнения
все решения уравнения 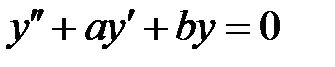 удовлетворяют соотношению
удовлетворяют соотношению 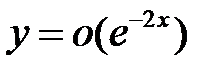 при
при 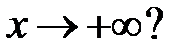
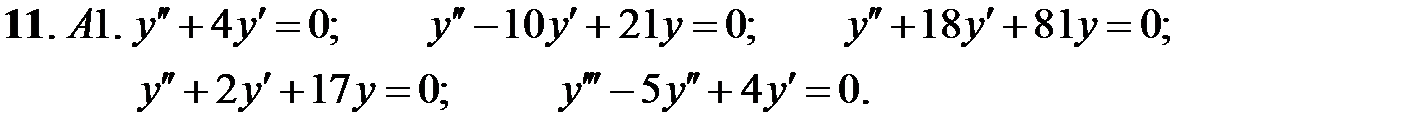
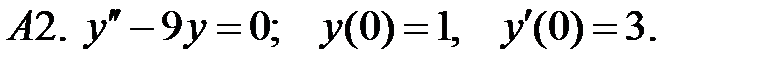
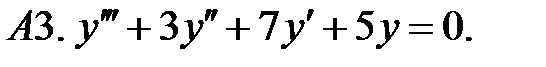
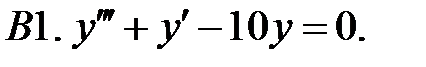
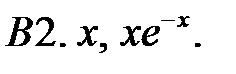
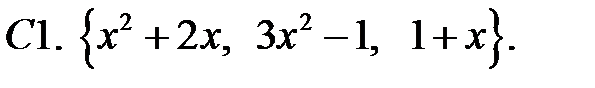
 При каких действительных
При каких действительных 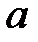 и
и 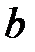 все решения уравнения
все решения уравнения 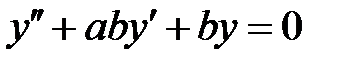 ограничены на всей числовой оси
ограничены на всей числовой оси 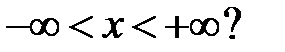
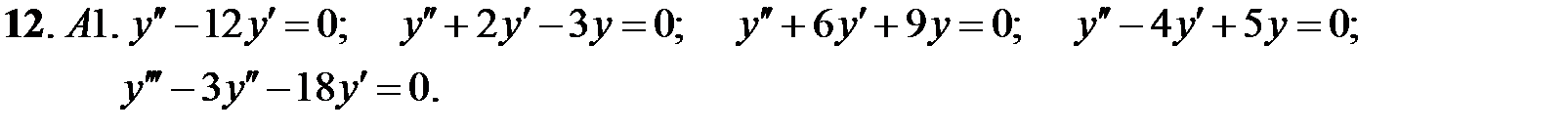
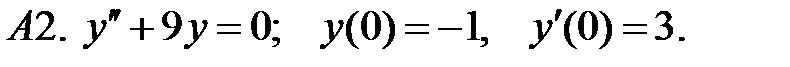
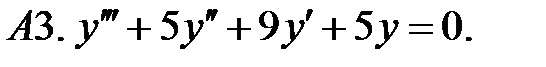
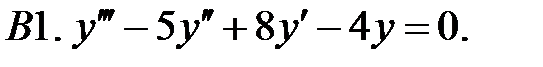
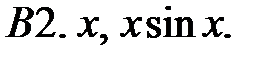
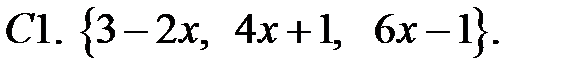
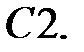 При каких действительных
При каких действительных 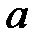 и
и 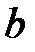 каждое решение уравнения
каждое решение уравнения 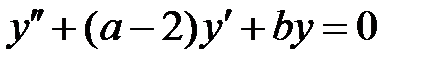 обращается в нуль на бесконечном множестве точек
обращается в нуль на бесконечном множестве точек 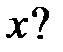
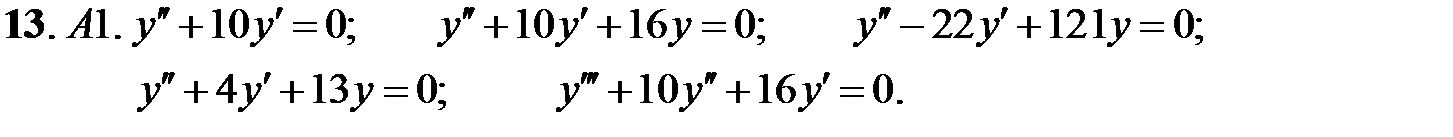
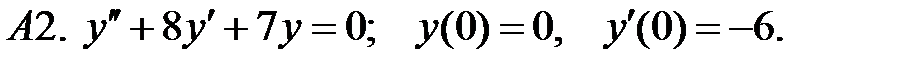
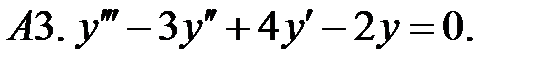
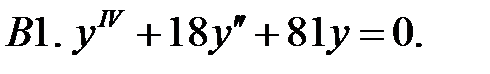
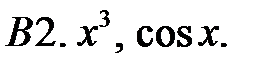
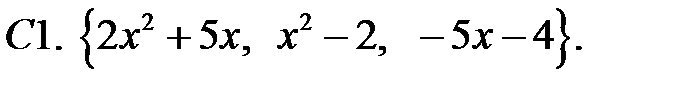
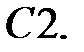 При каких действительных
При каких действительных 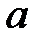 и
и 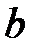 все решения уравнения
все решения уравнения 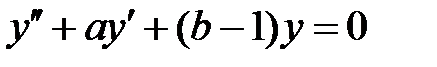 стремятся к нулю при
стремятся к нулю при 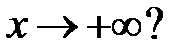
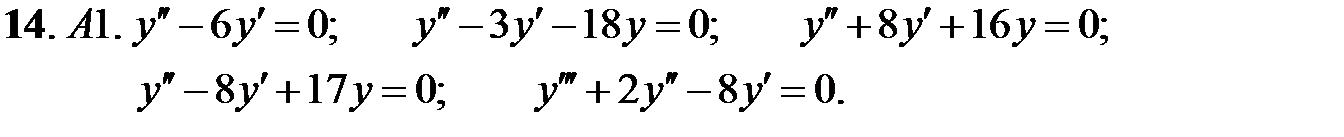
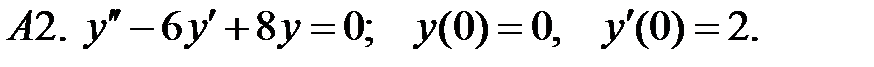
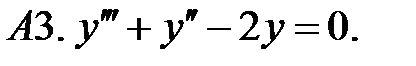
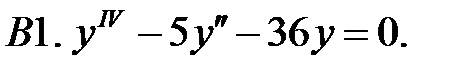
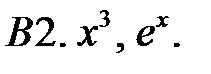
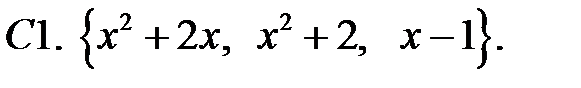
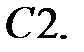 При каких
При каких 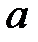 и
и 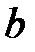 уравнение
уравнение 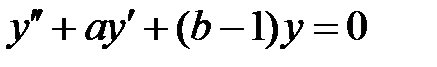 имеет хотя бы одно решение
имеет хотя бы одно решение 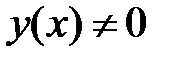 , стремящееся к нулю при
, стремящееся к нулю при 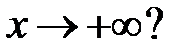
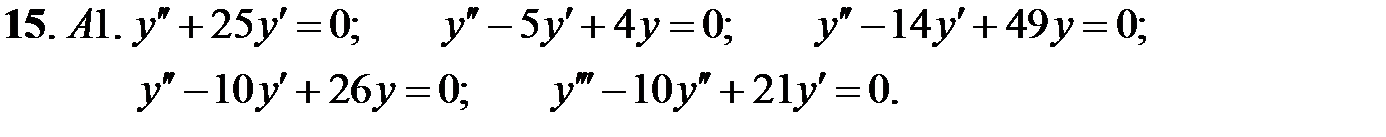
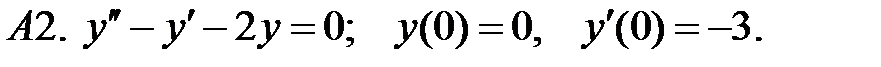
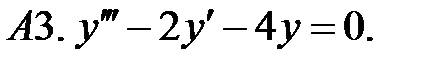
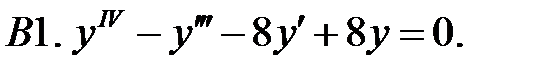
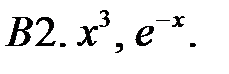
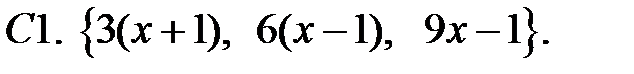
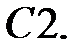 При каких действительных
При каких действительных 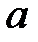 и
и 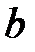 все решения уравнения
все решения уравнения 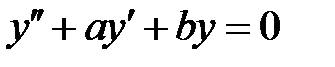 удовлетворяют соотношению
удовлетворяют соотношению 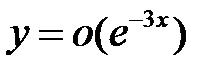 при
при 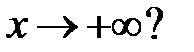
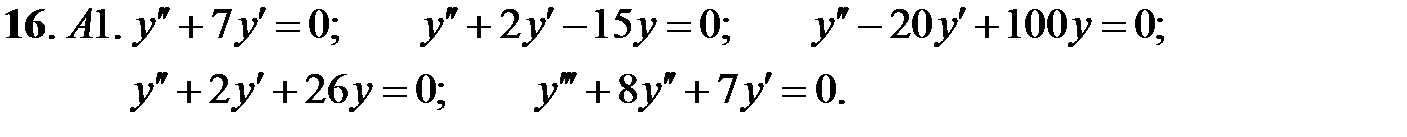
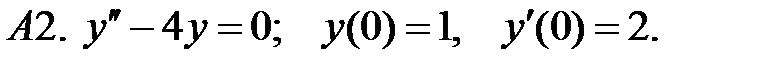
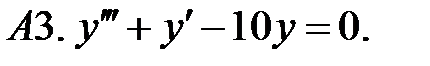
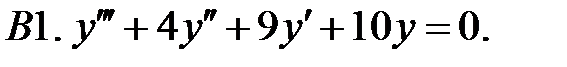
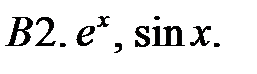
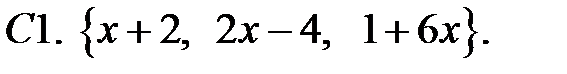
 При каких действительных
При каких действительных 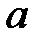 и
и 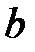 все решения уравнения
все решения уравнения 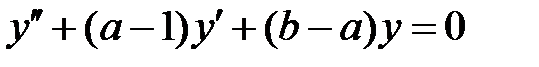 ограничены на всей числовой оси
ограничены на всей числовой оси 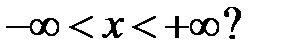
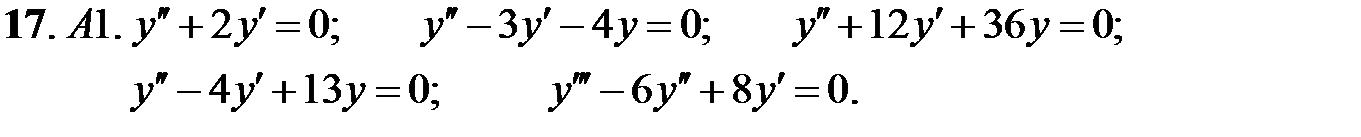
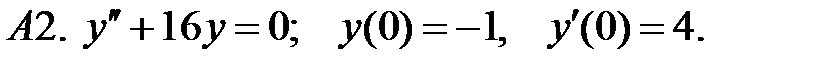
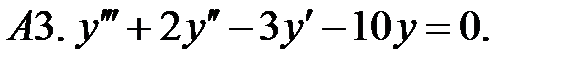
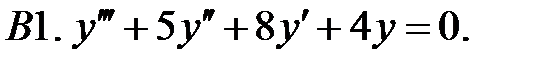
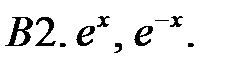
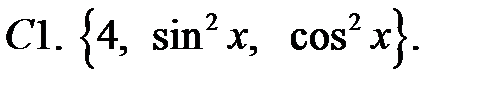
 При каких действительных
При каких действительных 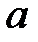 и
и 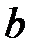 каждое решение уравнения
каждое решение уравнения 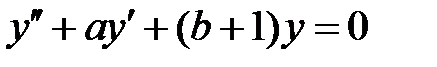 обращается в нуль на бесконечном множестве точек
обращается в нуль на бесконечном множестве точек 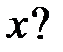
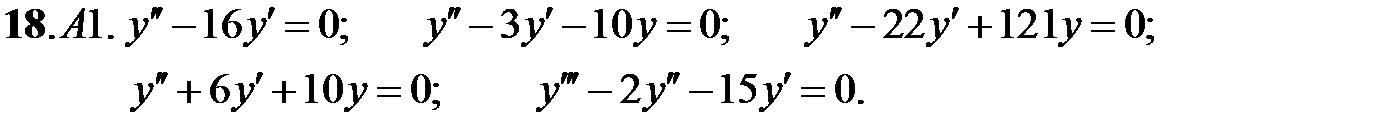
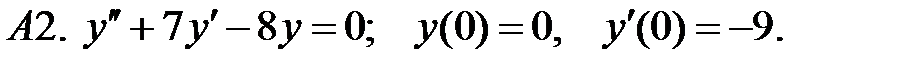
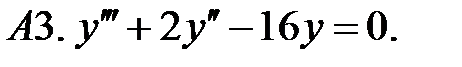
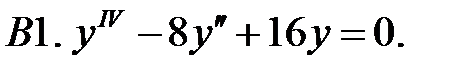
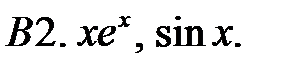
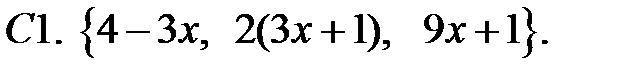
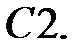 При каких
При каких 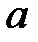 и
и 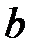 уравнение
уравнение 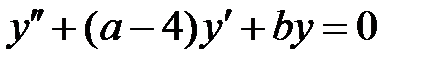 имеет хотя бы одно решение
имеет хотя бы одно решение 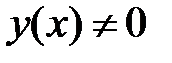 , стремящееся к нулю при
, стремящееся к нулю при 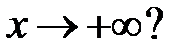
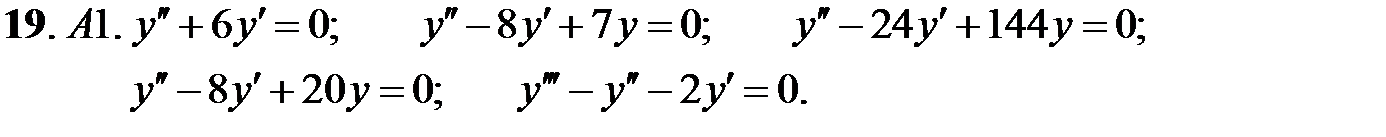
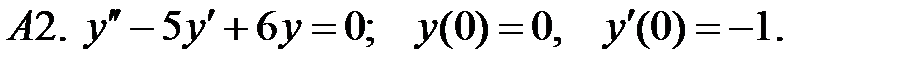
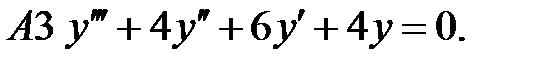
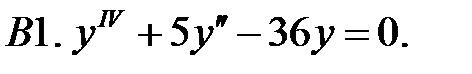
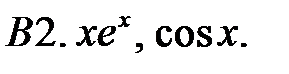
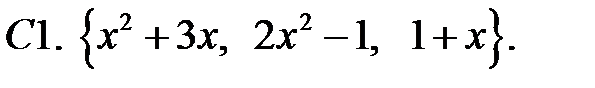
 При каких
При каких 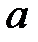 и
и 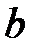 уравнение
уравнение 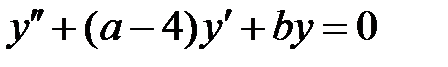 имеет хотя бы одно решение
имеет хотя бы одно решение 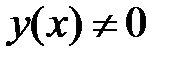 , стремящееся к нулю при
, стремящееся к нулю при 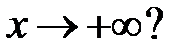
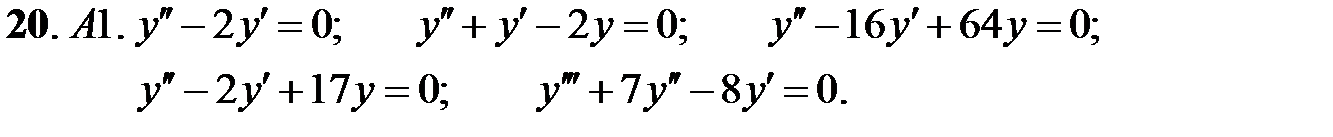
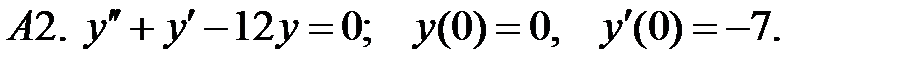
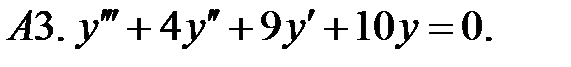
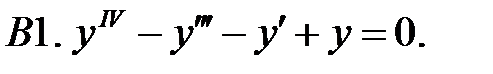
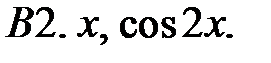
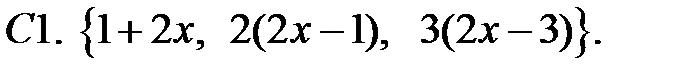
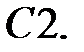 При каких действительных
При каких действительных 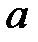 и
и 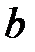 все решения уравнения
все решения уравнения 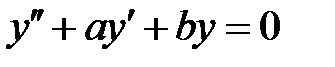 удовлетворяют соотношению
удовлетворяют соотношению 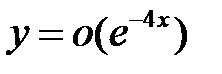 при
при 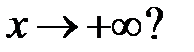
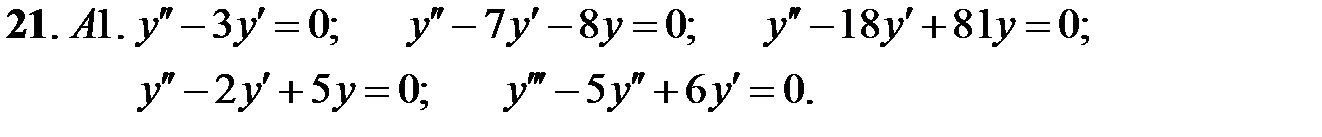
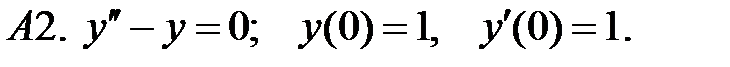
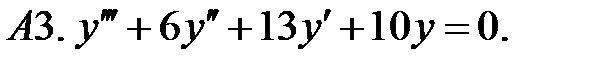
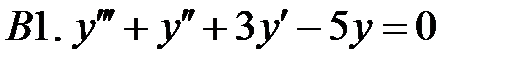
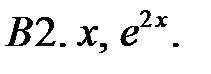
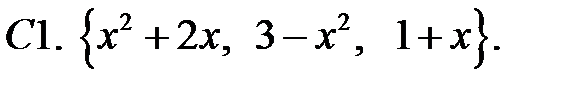
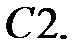 При каких действительных
При каких действительных 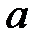 и
и 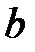 все решения уравнения
все решения уравнения 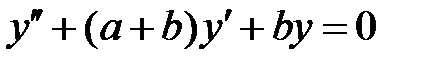 ограничены на всей числовой оси
ограничены на всей числовой оси 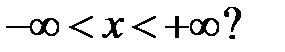
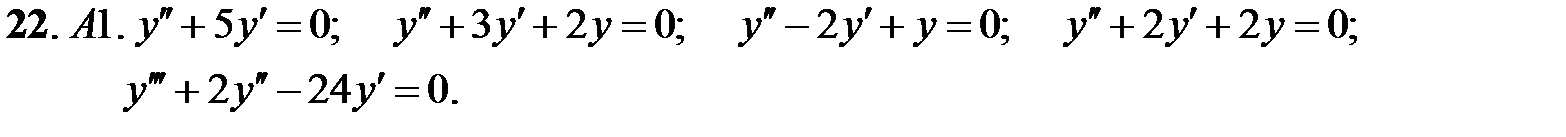
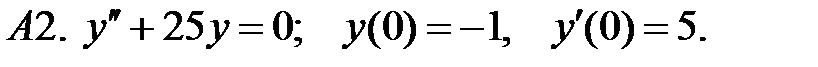
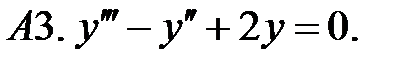
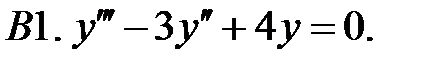
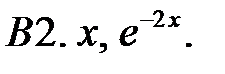
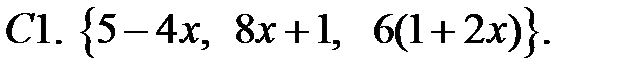
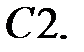 При каких действительных
При каких действительных 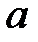 и
и 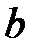 каждое решение уравнения
каждое решение уравнения 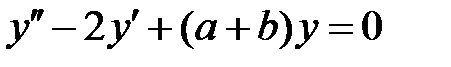 обращается в нуль на бесконечном множестве точек
обращается в нуль на бесконечном множестве точек 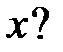
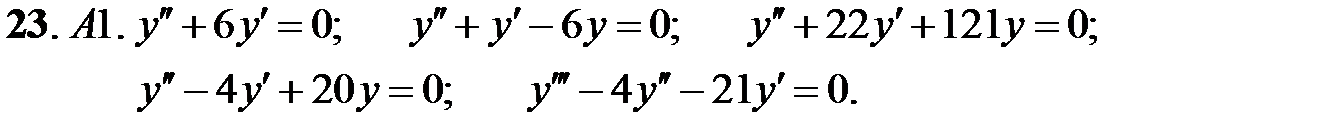
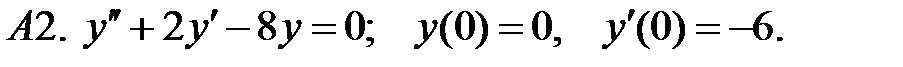
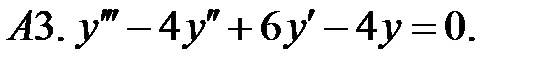
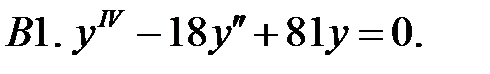
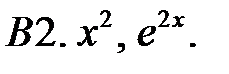
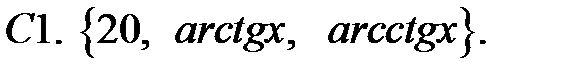
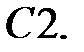 При каких действительных
При каких действительных 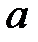 и
и 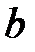 все решения уравнения
все решения уравнения 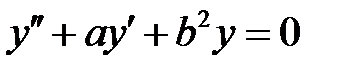 стремятся к нулю при
стремятся к нулю при 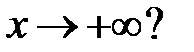
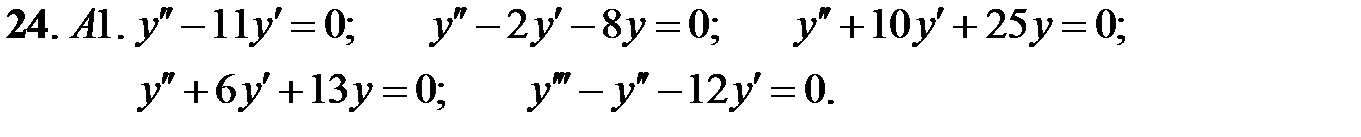
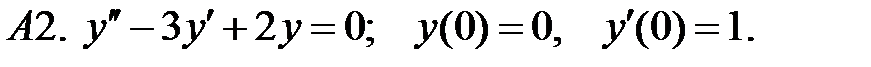
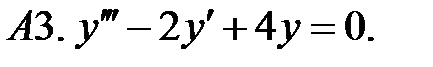
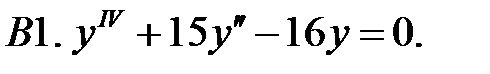
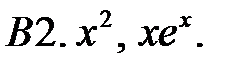
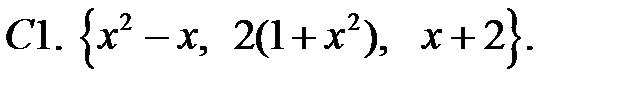
 При каких
При каких 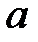 и
и 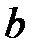 уравнение
уравнение 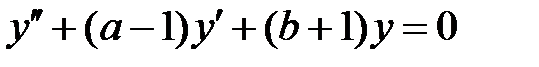 имеет хотя бы одно решение
имеет хотя бы одно решение 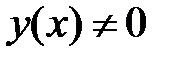 , стремящееся к нулю при
, стремящееся к нулю при 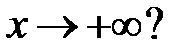
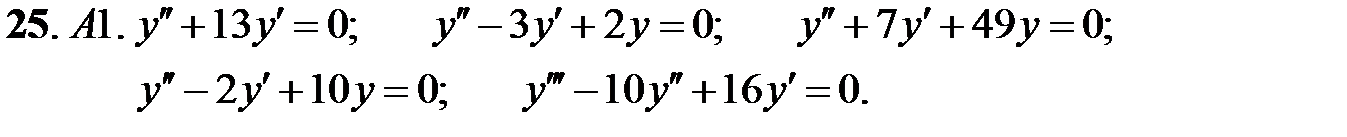
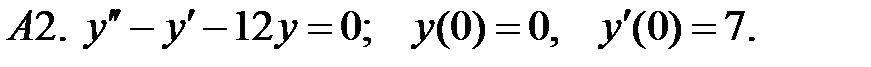
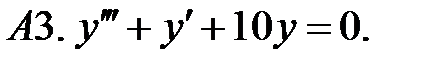
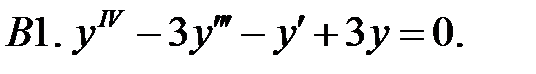
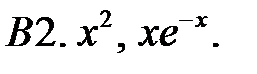
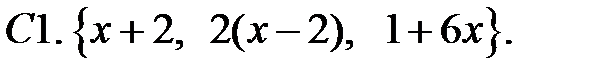
 При каких действительных
При каких действительных 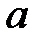 и
и 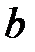 все решения уравнения
все решения уравнения 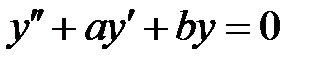 удовлетворяют соотношению
удовлетворяют соотношению 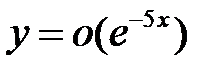 при
при