Линейные дифференциальные уравнения
5.1. Линейные уравнения с постоянными коэффициентами
Линейное неоднородное дифференциальное уравнение 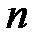 -го порядка имеет вид
-го порядка имеет вид
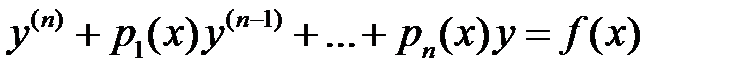 . (1)
. (1)
Здесь функции 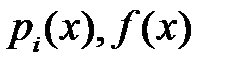
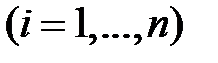 непрерывны на
непрерывны на 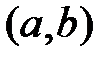 и принимают вещественные значения. Вместе с уравнением (1) рассмотрим соответствующее однородное уравнение
и принимают вещественные значения. Вместе с уравнением (1) рассмотрим соответствующее однородное уравнение
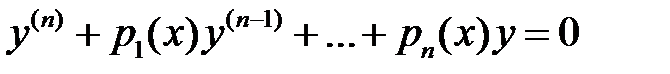 . (2)
. (2)
Линейное однородное уравнение всегда имеет решение 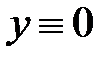 , которое называется тривиальным.
, которое называется тривиальным.
Функции 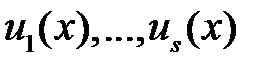 называются линейно зависимыми на
называются линейно зависимыми на 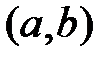 , если существуют постоянные
, если существуют постоянные 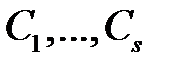 , не все равные нулю, такие, что имеет место тождество
, не все равные нулю, такие, что имеет место тождество
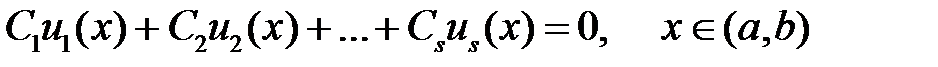 . (3)
. (3)
Если (3) выполняется только при 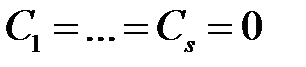 , то функции
, то функции 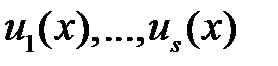 называются линейно независимыми.
называются линейно независимыми.
Пример 1. Показать, что система функций 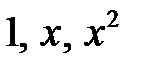 линейно независима на интервале
линейно независима на интервале 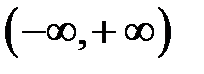 .
.
Решение. В самом деле, равенство
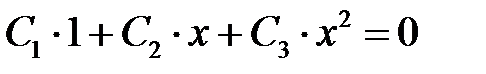
может выполняться для всех 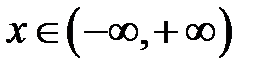 только при условии
только при условии 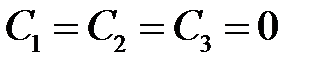 . Если же хотя бы одно их этих чисел не равно нулю, то в левой части равенства будем иметь многочлен степени не выше второй, а он может обращаться в нуль не более, чем при двух значениях
. Если же хотя бы одно их этих чисел не равно нулю, то в левой части равенства будем иметь многочлен степени не выше второй, а он может обращаться в нуль не более, чем при двух значениях 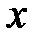 из данного интервала.
из данного интервала.
Пример 2. Исследовать на линейную зависимость следующие функции: 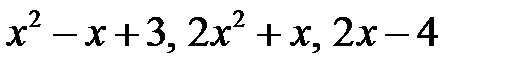 .
.
Решение. Выясним, можно ли найти такие постоянные 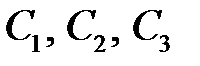 , чтобы на
, чтобы на 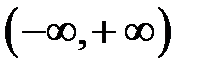 имело место тождество
имело место тождество
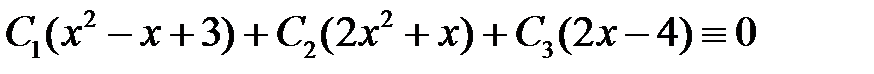
при 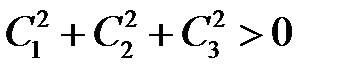 . Имеем
. Имеем
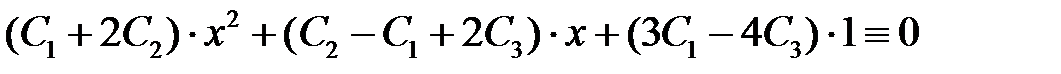 .
.
Поскольку функции 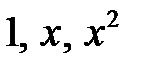 линейно независимы на
линейно независимы на 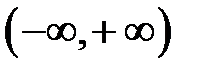 (см. предыдущий пример), то последнее тождество возможно при условиях
(см. предыдущий пример), то последнее тождество возможно при условиях
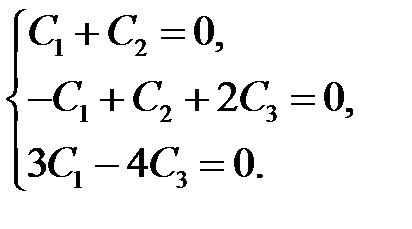
Так как главный определитель этой системы равен нулю, то наша система имеет нетривиальное решение (например, 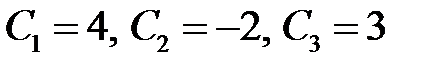 ). Следовательно, данные функции линейно зависимы.
). Следовательно, данные функции линейно зависимы.
Пример 3. Показать, что если
1) 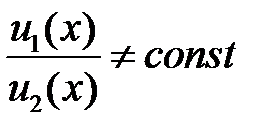 на
на  , то функции
, то функции 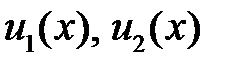 линейно независимы на
линейно независимы на 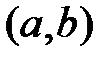 ;
;
2) 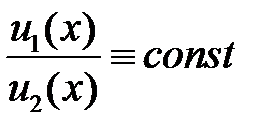 на
на 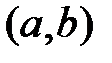 , то функции
, то функции 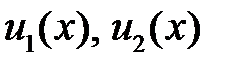 линейно зависимы на
линейно зависимы на 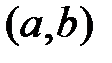 .
.
Решение. 1). Предположим, что 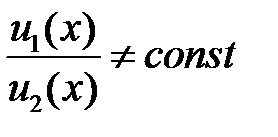 на
на 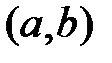 , но функции
, но функции 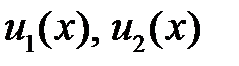 линейно зависимы на
линейно зависимы на 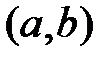 . Тогда имеет место тождество
. Тогда имеет место тождество
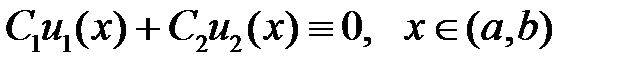 ,
,
причем 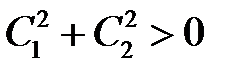 . Пусть, например,
. Пусть, например, 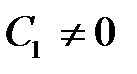 на
на 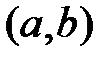 , имеем:
, имеем:
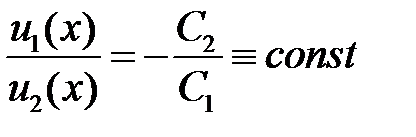 .
.
Это противоречит нашему предположению.
2). Предположим, что 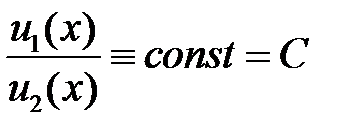 на
на 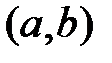 . Тогда имеет место тождество
. Тогда имеет место тождество 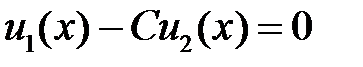 , причем, очевидно,
, причем, очевидно, 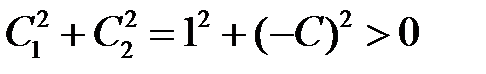 . Поэтому функции
. Поэтому функции 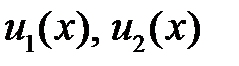 линейно зависимы на
линейно зависимы на 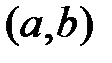 .
.
Фундаментальной системой решений называется система из 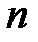 линейно независимых решений уравнения (2).
линейно независимых решений уравнения (2).
Теорема 1. Если 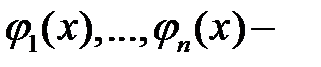 фундаментальная система решений (2), то для любого решения
фундаментальная система решений (2), то для любого решения 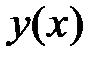 уравнения (2) существует единственный набор постоянных
уравнения (2) существует единственный набор постоянных 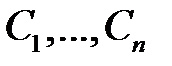 , такой, что
, такой, что
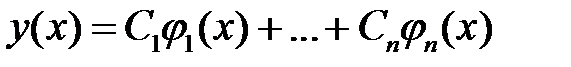 . (4)
. (4)
Поэтому общее решение уравнения (2) имеет вид (4), где 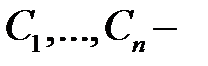 любые постоянные.
любые постоянные.
Если функции 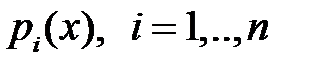 постоянны
постоянны 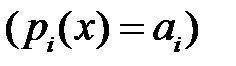 , то для построения фундаментальной системы решений применяется метод Эйлера. Ищем решения уравнения (2) в виде
, то для построения фундаментальной системы решений применяется метод Эйлера. Ищем решения уравнения (2) в виде 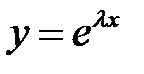 . Тогда получим тождество
. Тогда получим тождество 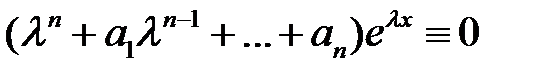 . Уравнение
. Уравнение
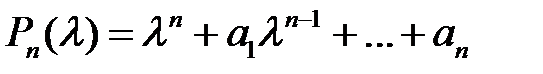 =0
=0
называется характеристическим для линейного однородного уравнения (2). Элементы фундаментальной системы решений находятся соответственно корням 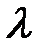 уравнения
уравнения 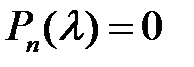 по следующему правилу:
по следующему правилу:
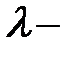 вещественный, простой
вещественный, простой 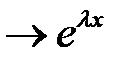 ;
;
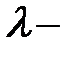 вещественный, кратности
вещественный, кратности 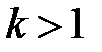
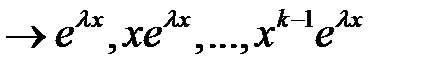 ;
;
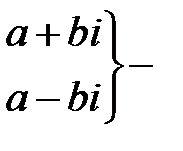 пара простых комплексно-сопряженных корней
пара простых комплексно-сопряженных корней 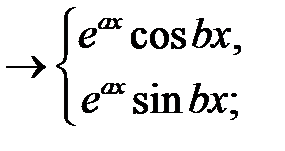
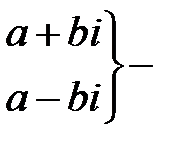 пара комплексно-сопряженных корней кратности
пара комплексно-сопряженных корней кратности 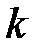
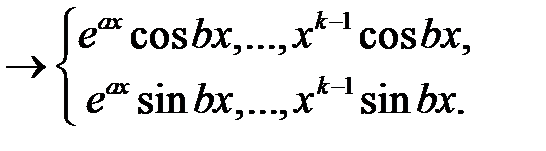
Пример 4. Найти общее решение уравнения 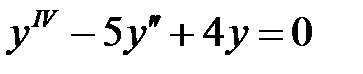 .
.
Решение. Составляем характеристическое уравнение
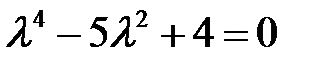 .
.
Находим его корни:
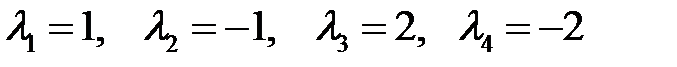 .
.
Так как они действительные и различные, то общее решение имеет вид
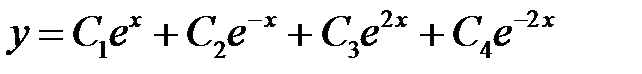 .
.
Пример 5. Найти общее решение уравнения 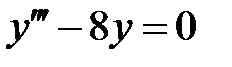 .
.
Решение. Характеристическое уравнение
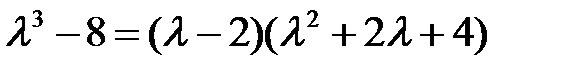 =0
=0
имеет корни
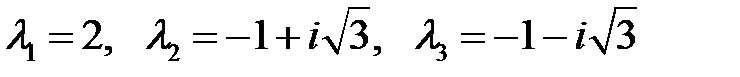 .
.
Общее решение имеет вид
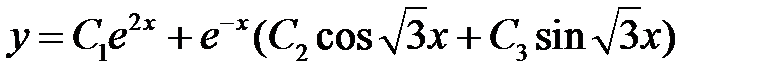 .
.
Пример 6. Найти общее решение уравнения 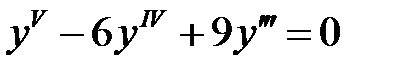 .
.
Решение. Характеристическое уравнение
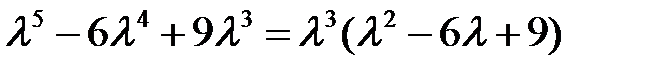 =0
=0
имеет корни 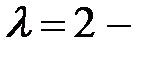 трехкратный и
трехкратный и 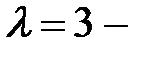 двукратный. Общее решение имеет вид
двукратный. Общее решение имеет вид
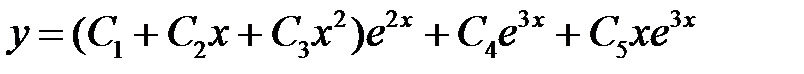 .
.
Пример 7. Найти общее решение уравнения
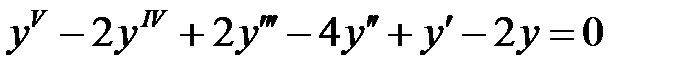 .
.
Решение. Составляем характеристическое уравнение
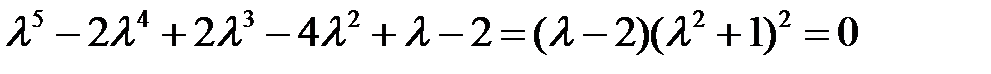 .
.
Оно имеет корни 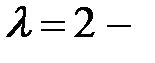 однократный и
однократный и 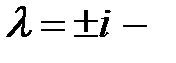 пара двукратных мнимых корней. Следовательно, общее решение имеет вид
пара двукратных мнимых корней. Следовательно, общее решение имеет вид
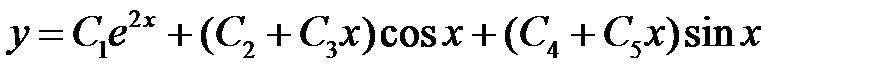 .
.
Задача Коши для линейного однородного уравнения (2) (линейного неоднородного уравнения (1)) ставится следующим образом: найти решение этого уравнения, удовлетворяющее начальным условиям
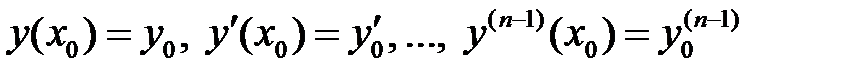 .
.
Пример 8. Найти решение задачи Коши
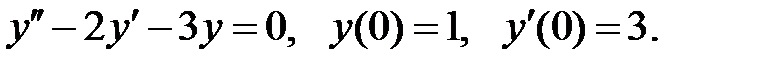
Решение. Характеристическое уравнение имеет вид
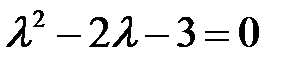 .
.
Решая его, получим корни 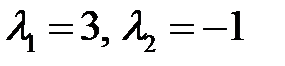 . Записываем общее решение уравнения
. Записываем общее решение уравнения
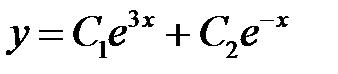 .
.
Теперь решаем задачу Коши, для этого вначале вычислим производную
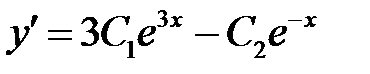 .
.
Используя начальные условия, имеем
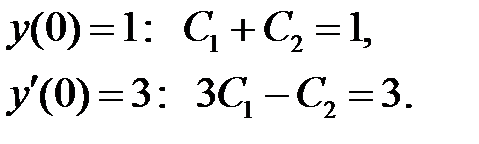
Отсюда находим 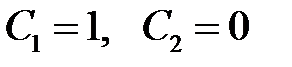 .
.
Наконец, можем записать окончательный вид частного решения исходного уравнения с заданными начальными условиями
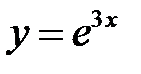 .
.
Пример 9. Составить линейное однородное уравнение с постоянными коэффициентами (возможно наименьшего порядка), имеющее следующие частные решения 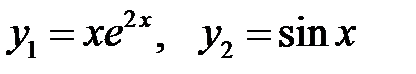 .
.
Решение. Частное решение 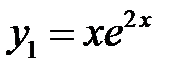 порождается двукратным корнем
порождается двукратным корнем 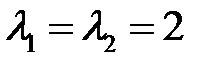 , а частное решение
, а частное решение 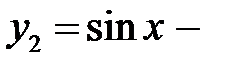 корнями
корнями 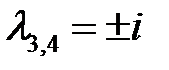 . Поскольку корни известны, то легко запишется характеристическое уравнение
. Поскольку корни известны, то легко запишется характеристическое уравнение
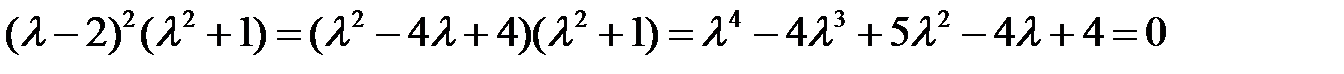 .
.
Ясно, что такому характеристическому уравнению соответствует дифференциальное уравнение
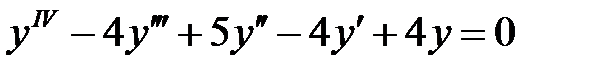 .
.
5.2. Метод неопределенных коэффициентов
Пусть 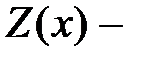 решение уравнения (1),
решение уравнения (1), 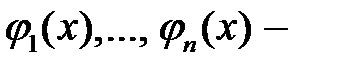 фундаментальная система решений соответствующего однородного уравнения (2). Тогда справедлива
фундаментальная система решений соответствующего однородного уравнения (2). Тогда справедлива
Теорема 2. Для любого решения 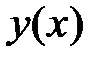 уравнения (1) существует единственный набор постоянных
уравнения (1) существует единственный набор постоянных 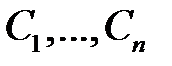 , такой, что
, такой, что
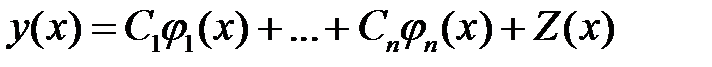 . (5)
. (5)
Отсюда, функция (5) является общим решением уравнения (1).
Для нахождения частного решения 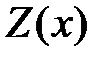 уравнения (1) используют метод неопределенных коэффициентов.
уравнения (1) используют метод неопределенных коэффициентов.
Пусть коэффициенты 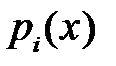 постоянны, а
постоянны, а 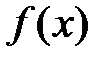 представима в виде
представима в виде
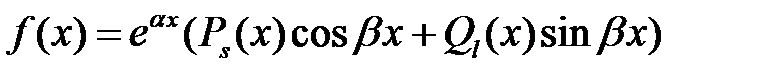 , (6)
, (6)
где 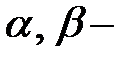 постоянные;
постоянные; 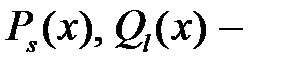 многочлены степени
многочлены степени 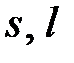 соответственно. Введем числа
соответственно. Введем числа 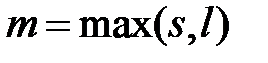 и
и

Теорема 3. Существует единственное решение 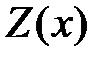 уравнение (1), имеющее вид
уравнение (1), имеющее вид
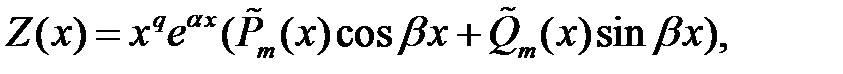 (7)
(7)
где 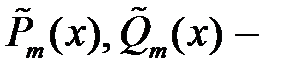 многочлены степени
многочлены степени 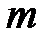 с неопределенными коэффициентами.
с неопределенными коэффициентами.
Для применения теоремы 3 функцию вида (7) подставляют в (1) и находят коэффициенты многочленов 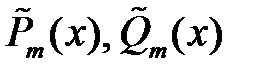 .
.
Пример 10. Решить уравнение 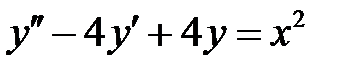 .
.
Решение. Характеристическое уравнение 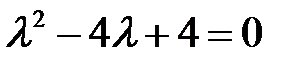 имеет кратные корни:
имеет кратные корни: 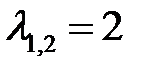 , поэтому общее решение
, поэтому общее решение 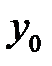 соответствующего однородного уравнения будет иметь вид:
соответствующего однородного уравнения будет иметь вид:
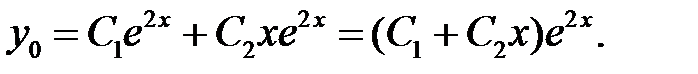
Так как число 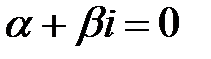 не является корнем характеристического уравнения, то частное решение данного уравнения надо искать в виде
не является корнем характеристического уравнения, то частное решение данного уравнения надо искать в виде
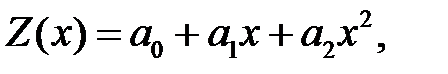
где 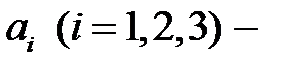 неизвестные пока коэффициенты, подлежащие определению. Подставляя выражение для
неизвестные пока коэффициенты, подлежащие определению. Подставляя выражение для 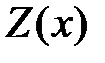 в данное уравнение, получаем
в данное уравнение, получаем
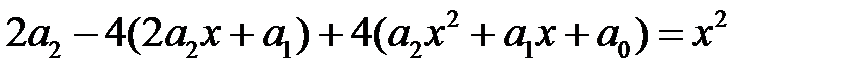 ,
,
откуда
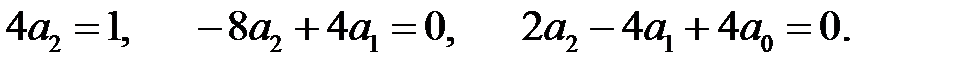
Решая эту систему, найдем 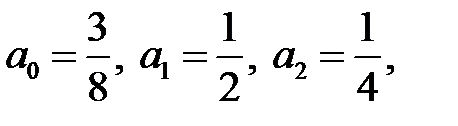 следовательно, частным решением будет
следовательно, частным решением будет
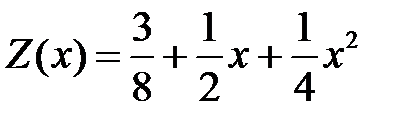 ,
,
и общее решение данного уравнения имеет вид
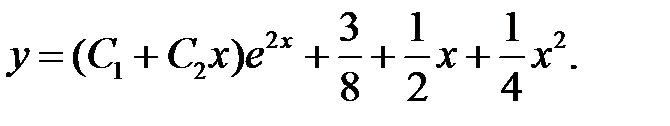
Пример 11. Решить уравнение 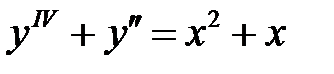 .
.
Решение. Характеристическое уравнение 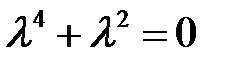 имеет корни
имеет корни 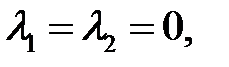
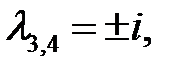 и поэтому общим решением соответствующего однородного уравнения будет функция
и поэтому общим решением соответствующего однородного уравнения будет функция
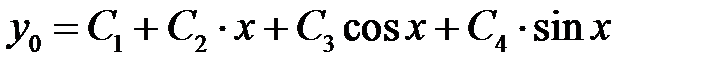 .
.
Так как число 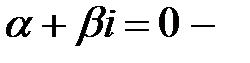 двукратный корень характеристического уравнения, то
двукратный корень характеристического уравнения, то 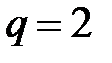 , и частное решение надо искать в виде
, и частное решение надо искать в виде
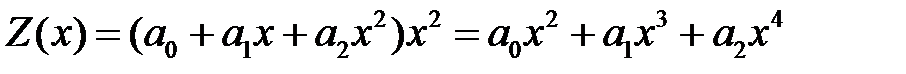 .
.
Подставляя выражение для 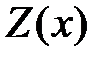 в данное уравнение, имеем
в данное уравнение, имеем
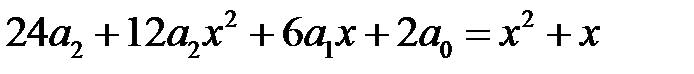 ,
,
откуда
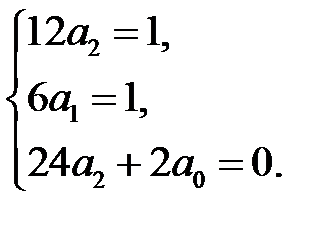
Эта система имеет решение: 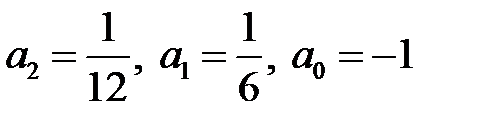 , а значит
, а значит
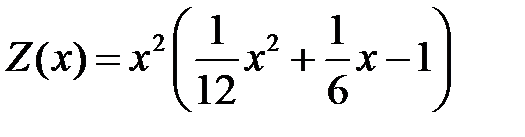 .
.
Общее решение данного уравнения имеет вид
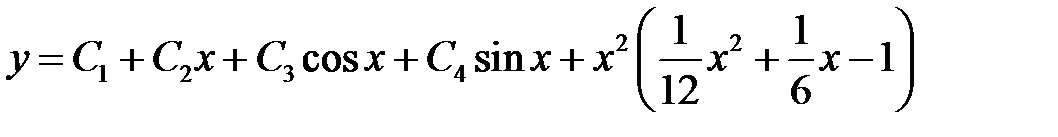 .
.
Пример 12. Решить уравнение 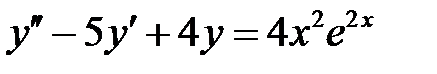 .
.
Решение. Характеристическое уравнение 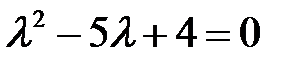 имеет корни
имеет корни 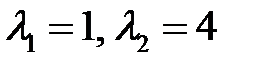 . Поэтому общее решение однородного уравнения имеет вид
. Поэтому общее решение однородного уравнения имеет вид
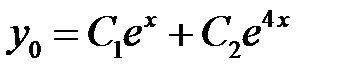 .
.
Число 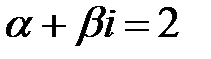 не является корнем характеристического уравнения, тогда частное решение
не является корнем характеристического уравнения, тогда частное решение 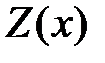 неоднородного уравнения ищем в виде
неоднородного уравнения ищем в виде
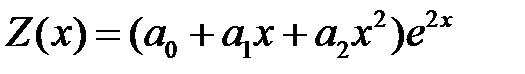 .
.
Подставляя его в исходное уравнение и сокращая обе части на 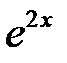 , будем иметь
, будем иметь
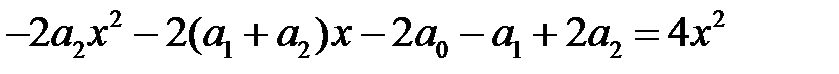 .
.
Приравнивая коэффициенты при одинаковых степенях 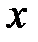 в левой и правой частях равенства, получаем линейную систему для нахождения коэффициентов
в левой и правой частях равенства, получаем линейную систему для нахождения коэффициентов 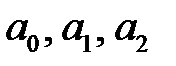 :
:
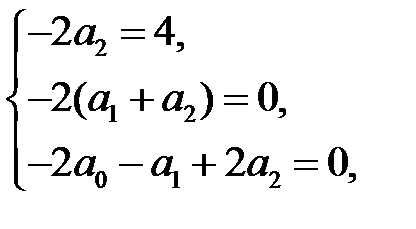
решая которую, находим 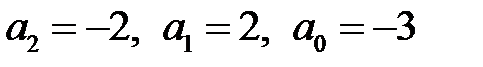 , так что
, так что
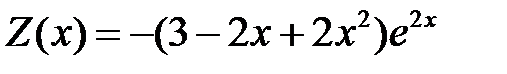 .
.
Следовательно, общее решение данного уравнения имеет вид
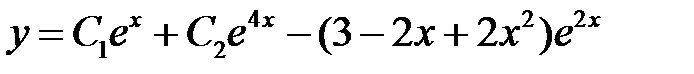 .
.
Пример 13. Решить уравнение 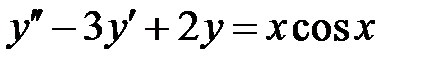 .
.
Решение. Характеристическое уравнение 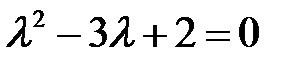 имеет корни
имеет корни 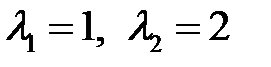 , поэтому
, поэтому
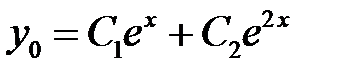 .
.
Так как число 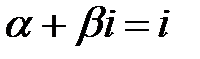 не является корнем характеристического уравнения, то
не является корнем характеристического уравнения, то 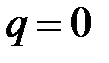 и частное решение ищем в виде
и частное решение ищем в виде
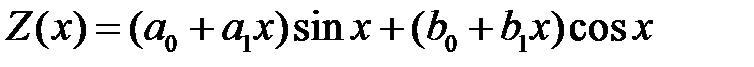 .
.
Подставляя его в исходное уравнение имеем
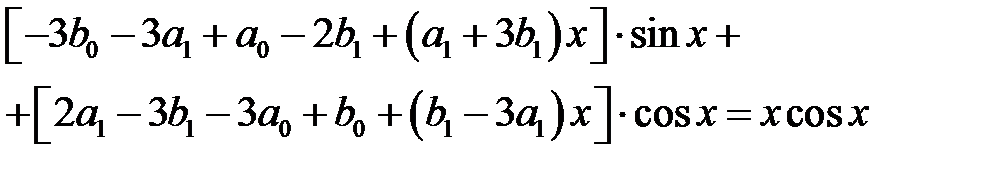 .
.
Отсюда получаем систему относительно 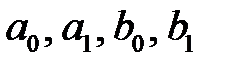 :
:
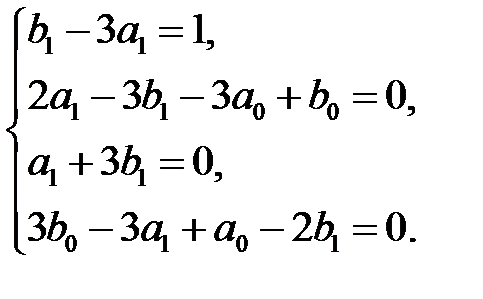
Решая эту систему, найдем 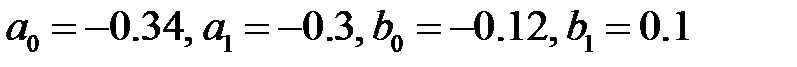 и частное решение запишется так:
и частное решение запишется так:
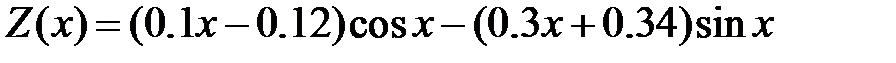 .
.
Общее решение исходного уравнения
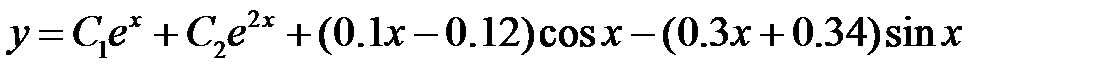 .
.
Пример 14. Решить уравнение 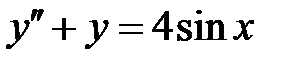 .
.
Решение. Характеристическое уравнение имеет корни 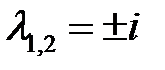 , поэтому общее решение однородного уравнения имеет вид
, поэтому общее решение однородного уравнения имеет вид
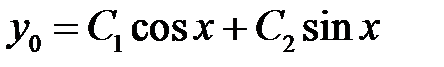 .
.
Число 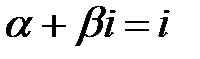 является корнем характеристического уравнения, тогда
является корнем характеристического уравнения, тогда 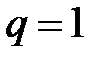 и частное решение неоднородного уравнения надо искать в виде
и частное решение неоднородного уравнения надо искать в виде
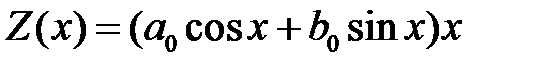 .
.
Подставляя полученное выражение в исходное уравнение, находим 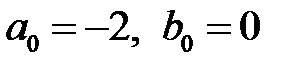 .
.
Отсюда
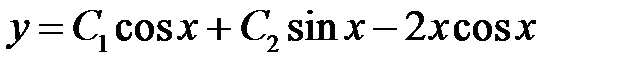 .
.
Пример 15. Решить уравнение 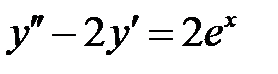 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям
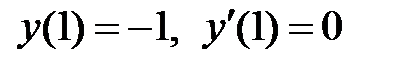 . (*)
. (*)
Решение. Находим общее решение уравнения:
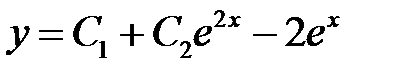 . (**)
. (**)
Для решения задачи Коши требуется определить значения постоянных  и
и  так, чтобы решение (**) удовлетворяло начальным условиям (*). Используя условие
так, чтобы решение (**) удовлетворяло начальным условиям (*). Используя условие 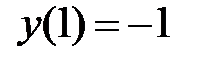 , получаем
, получаем
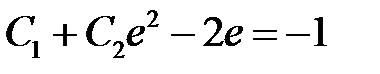 .
.
Дифференцируя (**), найдем
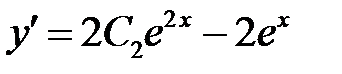 ,
,
откуда, в силу условия 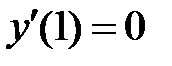 , будем иметь
, будем иметь
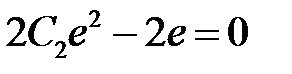 .
.
Для отыскания 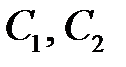 получим систему
получим систему
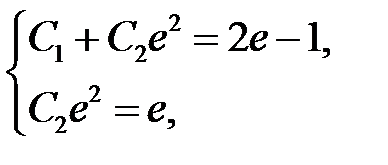
решая которую, находим 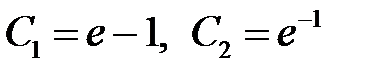 . Подставляя найденные значения произвольных постоянных в общее решение (**), получим решение задачи Коши
. Подставляя найденные значения произвольных постоянных в общее решение (**), получим решение задачи Коши
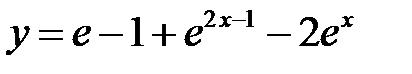 .
.
Пример 16. Определить вид частного решения уравнения
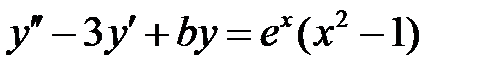 .
.
Решение. Запишем отдельно правую часть уравнения 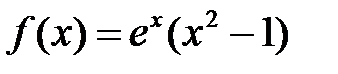 , где
, где 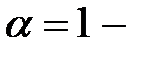 контрольное число,
контрольное число, 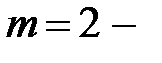 порядок многочлена. Различаем два случая
порядок многочлена. Различаем два случая 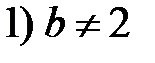 и
и 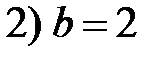 , так как характеристическое уравнение
, так как характеристическое уравнение
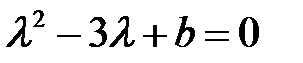 (*)
(*)
при 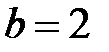 имеет корень
имеет корень 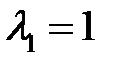 .
.
В первом случае контрольное число 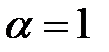 не совпадает с корнями характеристического уравнения (*), следовательно, частное решение имеет вид
не совпадает с корнями характеристического уравнения (*), следовательно, частное решение имеет вид
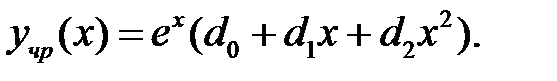
Во втором случае, при 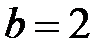 , характеристическое уравнение имеет корень
, характеристическое уравнение имеет корень 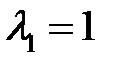 , который совпадает с контрольным числом
, который совпадает с контрольным числом 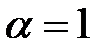 . Заметим, что кратность этого корня
. Заметим, что кратность этого корня 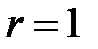 . Поэтому частное решение ищется в виде:
. Поэтому частное решение ищется в виде:
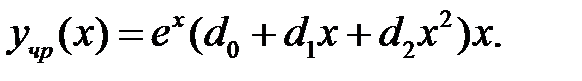
Задача Коши для линейного неоднородного уравнения (1): найти решение этого уравнения, удовлетворяющее начальным условиям
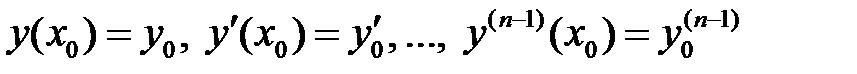 .
.
5.3. Метод Лагранжа (вариации произвольных постоянных)
Другим методом нахождения частного решения линейного неоднородного уравнения (1) является метод Лагранжа или метод вариации произвольных постоянных.
Этот метод применим как для уравнений с правыми частями специального вида (6), так и в случае правых частей общего вида.
Пусть известна фундаментальная система решений 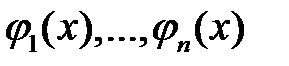 уравнения (2). Если для функций
уравнения (2). Если для функций 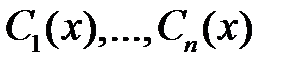 класса
класса 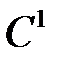 выполнены соотношения
выполнены соотношения
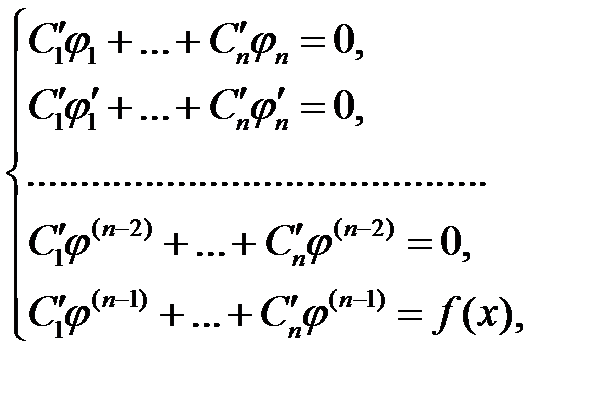 (8)
(8)
то 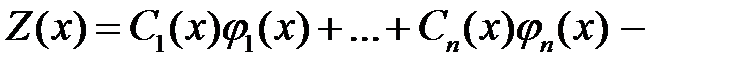 решение уравнения (1).
решение уравнения (1).
Пример 17. Решить уравнение 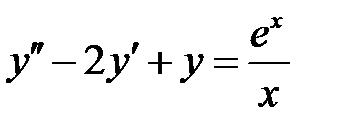 .
.
Решение. Так как правая часть уравнения не представима в виде (6), то общее решение может быть найдено методом вариации произвольных постоянных (методом Лагранжа). Общее решение однородного уравнения имеет вид
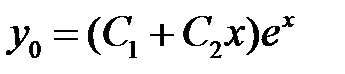 .
.
Составим систему (8):
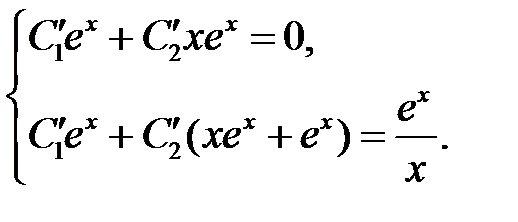
Отсюда
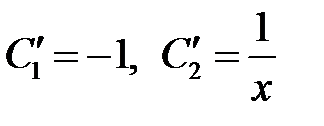 .
.
На 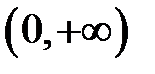 , выбирая
, выбирая 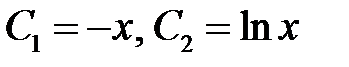 , получим
, получим
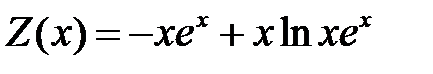 .
.
Следовательно, общее решение представимо в виде
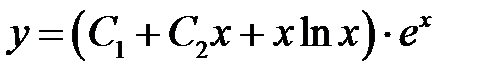 .
.
Пример 18. Решить уравнение 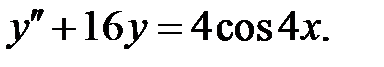
Решение. Соответствующее однородное уравнение
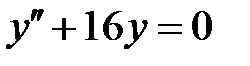
имеет следующую ФСР= 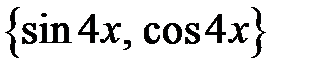 . Будем искать частное решение в виде
. Будем искать частное решение в виде
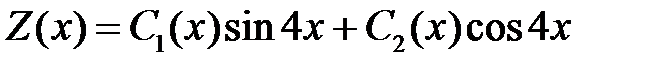 .
.
Из системы алгебраических уравнений
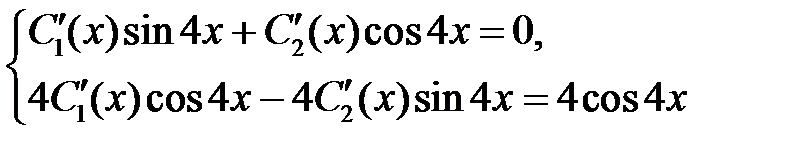
легко находим 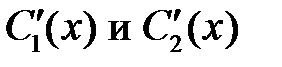 :
:
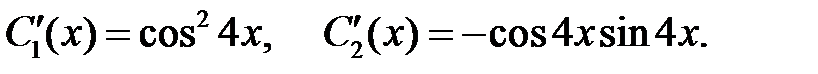
Откуда
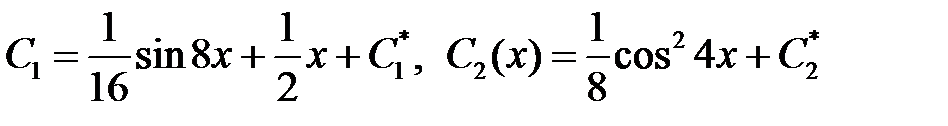 .
.
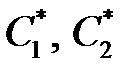 можем взять нулями. Следовательно,
можем взять нулями. Следовательно,
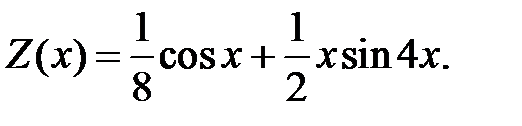
Отсюда
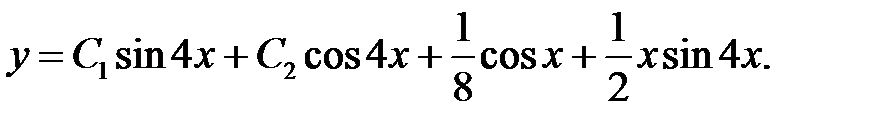
Пример 19. Найти решение уравнения 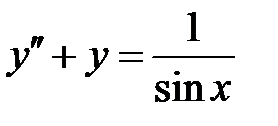 , удовлетворяющее условиям
, удовлетворяющее условиям 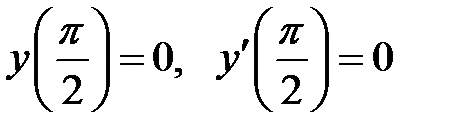 .
.
Решение. Решив известным способом соответствующее однородное уравнение, имеем
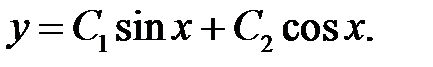
Для получения частного решения неоднородного уравнения воспользуемся методом Лагранжа.
Частное решение исходного уравнения ищем в виде
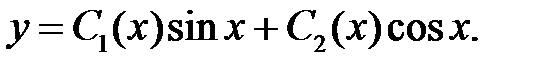
Система для определения 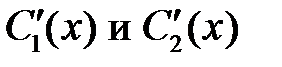 примет вид
примет вид
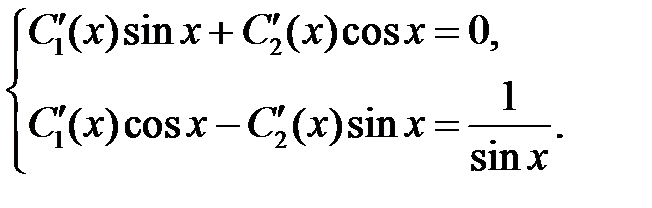
Решая её, получим
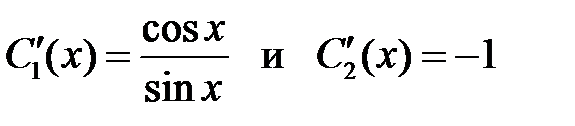 ,
,
откуда (ограничиваясь некоторым решением) находим
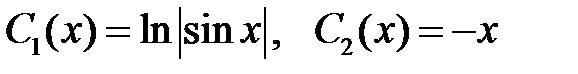 .
.
Тогда
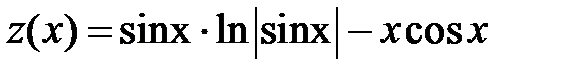
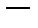 частное решение линейного неоднородного уравнения и
частное решение линейного неоднородного уравнения и
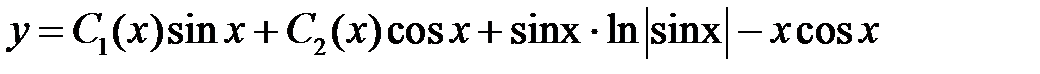
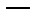 общее решение исходного уравнения.
общее решение исходного уравнения.
Вычислим производную
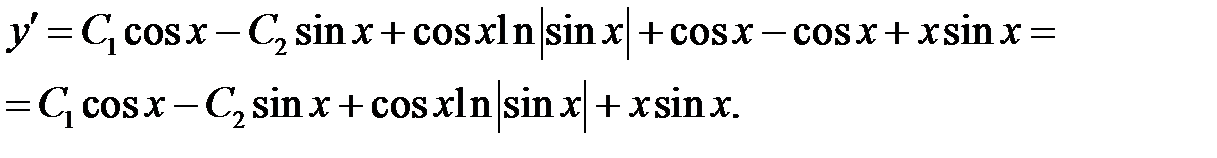
Учитывая начальные условия, составим систему
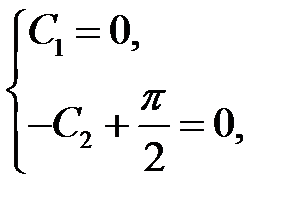
откуда 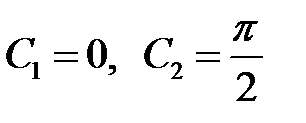 .
.
Решение задачи Коши имеет вид
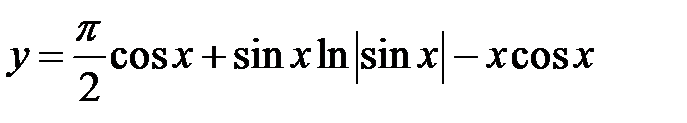 .
.
5.4. Принцип суперпозиции
Если 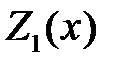
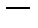 решение уравнения
решение уравнения
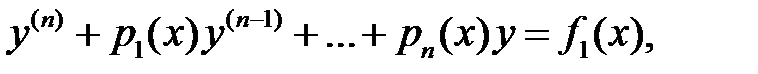
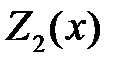
 решение уравнения
решение уравнения
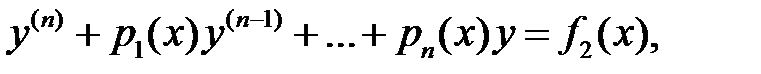
то 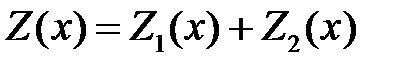
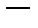 решение уравнения
решение уравнения
Пример 20. Решить уравнение 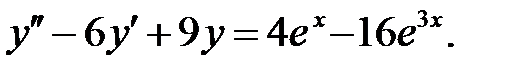
Решение. Характеристическое уравнение 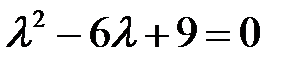 имеет корни
имеет корни 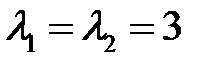 , а поэтому общим решением соответствующего однородного уравнения будет
, а поэтому общим решением соответствующего однородного уравнения будет
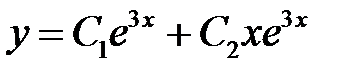 .
.
Для нахождения частного решения данного уравнения найдем частные решения двух уравнений
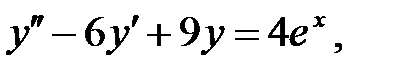 (*)
(*)
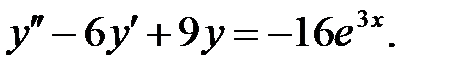 (**)
(**)
Первое из этих уравнений имеет частное решение 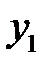 вида
вида 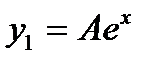 . Подставляя выражение для
. Подставляя выражение для 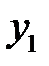 в уравнение (*), найдем
в уравнение (*), найдем 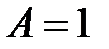 , так что
, так что 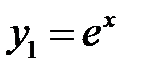 . Частное решение уравнения (**) ищем в виде
. Частное решение уравнения (**) ищем в виде 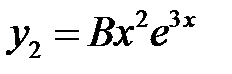 . Находим
. Находим 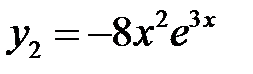 .
.
В силу принципа суперпозиции решений частное решение 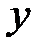 данного уравнения будет равно сумме частных решений
данного уравнения будет равно сумме частных решений 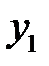 и
и 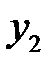 уравнений (*) и (**):
уравнений (*) и (**):
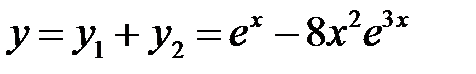 .
.
Общее решение уравнения
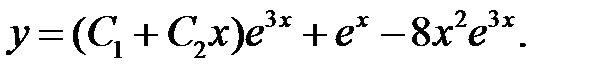
Пример 21. Решить уравнение 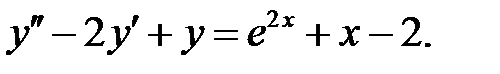
Решение. Характеристическое уравнение
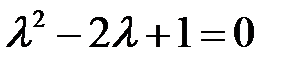
имеет корни 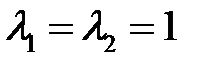 , а поэтому общим решением соответствующего однородного уравнения будет
, а поэтому общим решением соответствующего однородного уравнения будет
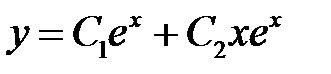 .
.
Для нахождения частного решения исходного уравнения найдем частные решения двух уравнений
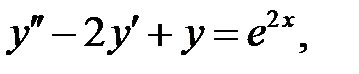
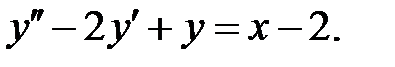
Первое уравнение имеет частное решение 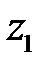 вида
вида 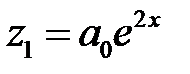 , а второе
, а второе 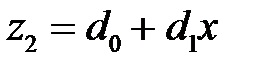 . Методом неопределенных коэффициентов находим неизвестные коэффициенты, и частными решениями будут
. Методом неопределенных коэффициентов находим неизвестные коэффициенты, и частными решениями будут 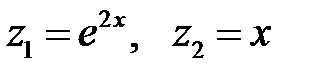 .
.
В силу принципа суперпозиции общее решение исходного уравнения имеет вид
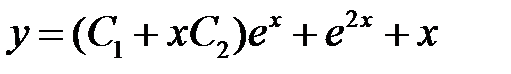 .
.
Пример 22. Определить вид частного решения (не находя числовые значения коэффициентов) уравнения 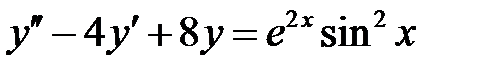 .
.
Решение. Прежде всего находим корни характеристического уравнения 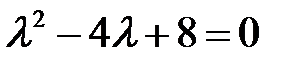 :
: 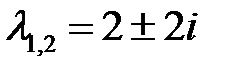 . Далее, запишем правую часть уравнения в виде
. Далее, запишем правую часть уравнения в виде
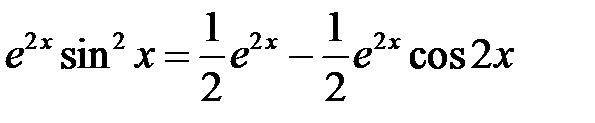 .
.
Для первого уравнения
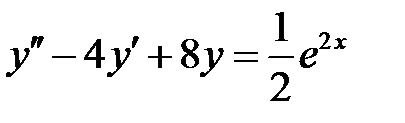
имеем 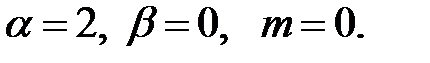 Так как контрольное число
Так как контрольное число 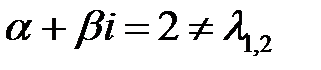 , то частное решение имеет вид
, то частное решение имеет вид
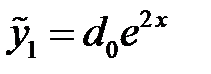 .
.
Для второго уравнения
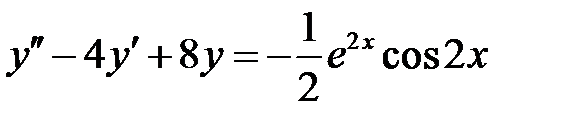
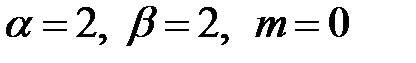 , то
, то 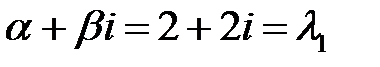 . Следовательно,
. Следовательно,
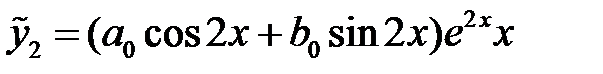 .
.
Сумма этих частных решений и есть частное решение данного уравнения.
5.5. Линейные уравнения с переменными коэффициентами
Если известно частное решение 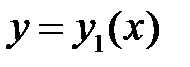 однородного уравнения (2), то его порядок можно понизить на единицу, сохраняя линейность уравнения. Для этого в уравнение надо подставить
однородного уравнения (2), то его порядок можно понизить на единицу, сохраняя линейность уравнения. Для этого в уравнение надо подставить 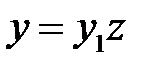 , где
, где 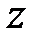 – новая неизвестная функция и затем понизить порядок заменой
– новая неизвестная функция и затем понизить порядок заменой 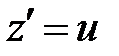 .
.
Чтобы найти общее решение линейного однородного уравнения второго порядка, у которого известно одно частое решение 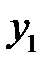 , можно понизить порядок уравнения указанным выше способом. Однако удобнее воспользоваться формулой Остроградского-Лиувилля:
, можно понизить порядок уравнения указанным выше способом. Однако удобнее воспользоваться формулой Остроградского-Лиувилля:
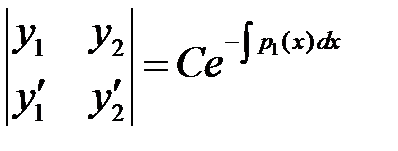 , или
, или 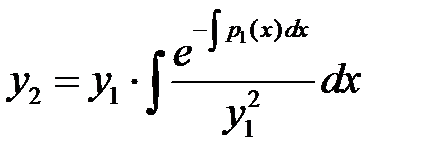 ,
,
где 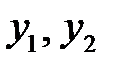 – любые линейно-независимые решения данного уравнения.
– любые линейно-независимые решения данного уравнения.
Пример 23. Решить уравнение 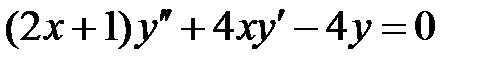 .
.
Решение. Общего метода для отыскания частного решения линейного уравнения второго порядка с переменными коэффициентами не существует. В некоторых случаях решение удастся найти путем подбора.
Ищем частное решение данного уравнения в виде многочлена
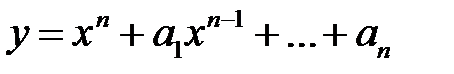 .
.
Коэффициент при старшем члене можно считать равным единице, так как решение линейного однородного уравнения можно умножить на произвольную постоянную. Подставляя многочлен в исходное уравнение и требуя, чтобы коэффициент при старшей степени обратился в нуль, получим 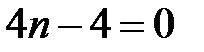 , откуда
, откуда 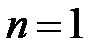 .
.
Если бы мы не получили ни одного целого положительного корня, то не существовало бы решения в виде многочлена. Итак, решение однородного уравнения может иметь вид: 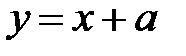 . Подставляя его в уравнение, получаем
. Подставляя его в уравнение, получаем 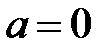 . Теперь можно понизить порядок данного уравнения на единицу подстановкой
. Теперь можно понизить порядок данного уравнения на единицу подстановкой 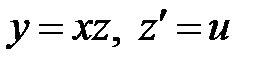 , или воспользоваться формулой Остроградского-Лиувилля:
, или воспользоваться формулой Остроградского-Лиувилля:
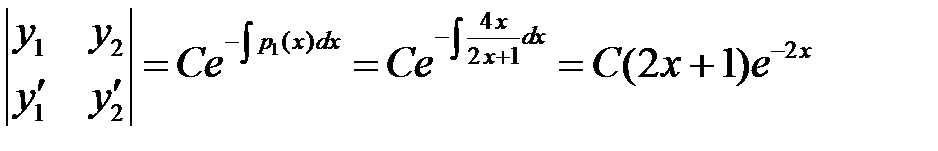 ;
;
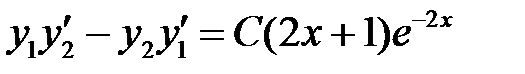 .
.
Так как функция 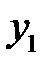 известна, то мы получили линейное уравнение первого порядка относительно
известна, то мы получили линейное уравнение первого порядка относительно 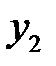 . Проще всего оно решается следующим способом. Разделив обе части уравнения на
. Проще всего оно решается следующим способом. Разделив обе части уравнения на 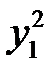 , получим слева производную от дроби
, получим слева производную от дроби 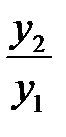 :
:
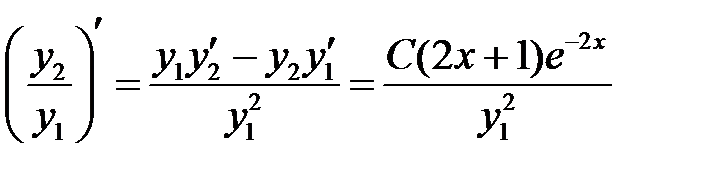 .
.
Так как 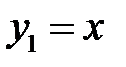 , то
, то
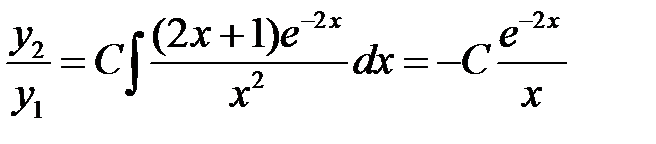 ;
;
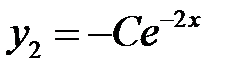 .
.
Следовательно, общее решение уравнения имеет вид
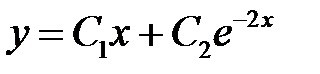 .
.
Пример 24. Решить уравнение 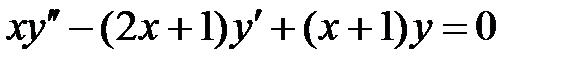 .
.
Решение. Ищем частное решение в виде показательной функции 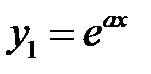 . Подставляя её в исходное уравнение, получим
. Подставляя её в исходное уравнение, получим 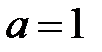 . Как и в примере 23, находим:
. Как и в примере 23, находим:
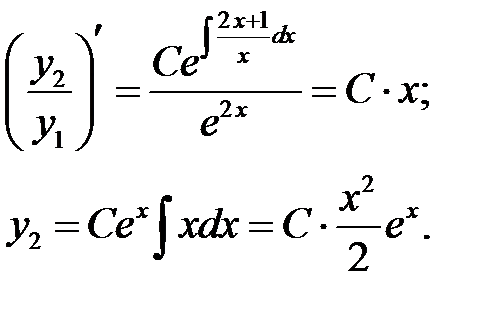
Общее решение данного уравнения имеет вид
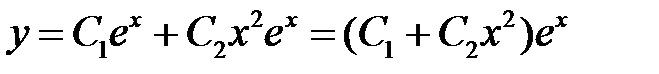 .
.
5.6. Уравнения Эйлера
Линейное уравнение вида
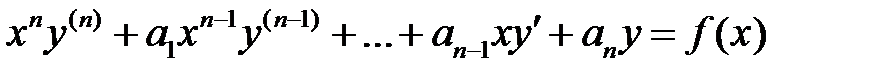 , (9)
, (9)
где все 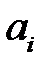
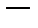 постоянные, называется уравнением Эйлера. Это уравнение сводится к линейному уравнению с постоянными коэффициентами заменой независимой переменной:
постоянные, называется уравнением Эйлера. Это уравнение сводится к линейному уравнению с постоянными коэффициентами заменой независимой переменной: 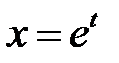 при
при 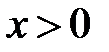 (или
(или 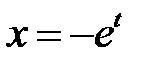 при
при 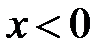 ). Для полученного уравнения с постоянными коэффициентами характеристическое уравнение имеет вид
). Для полученного уравнения с постоянными коэффициентами характеристическое уравнение имеет вид
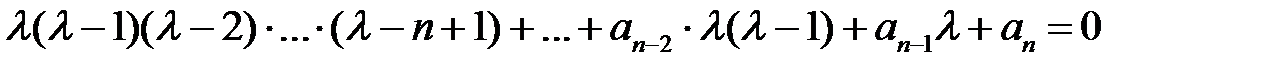 .
.
При составлении этого уравнения каждое произведение 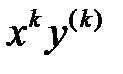 в (9) заменяется на произведение
в (9) заменяется на произведение 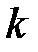 убывающих на 1 чисел
убывающих на 1 чисел
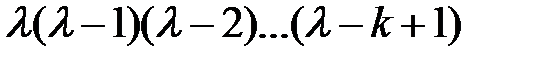 .
.
Замечание 1. Уравнение вида
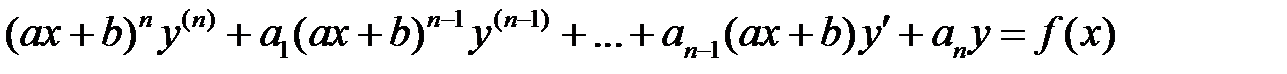
также называется уравнением Эйлера и сводится к линейному уравнению с постоянными коэффициентами заменой 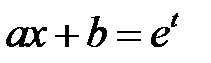 .
.
Замечание 2. Частные решения уравнения Эйлера можно сразу искать в виде 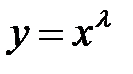 .
.
Пример 25. Решить уравнение 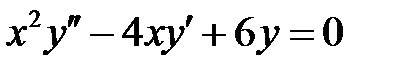 .
.
Решение. Первый способ. Сразу ищем характеристическое уравнение и решаем его:
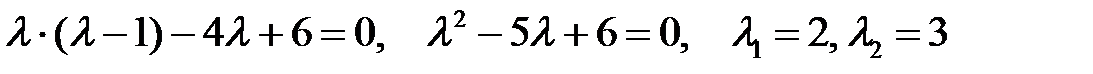 .
.
Следовательно, общим решением преобразованного уравнения будет функция
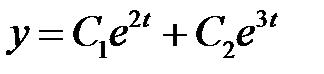 .
.
Но так как 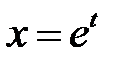 , то
, то
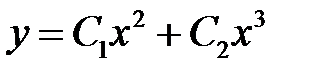 .
.
Второй способ. Будем искать решение данного уравнения в виде 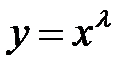 , где
, где 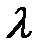 – неизвестное число. Подставляя
– неизвестное число. Подставляя 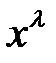 в уравнение, получаем
в уравнение, получаем
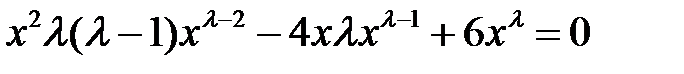 ,
,
или
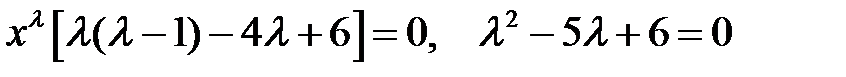 .
.
Корни этого уравнения 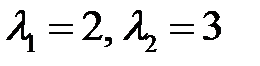 . Им соответствует фундаментальная система решений
. Им соответствует фундаментальная система решений 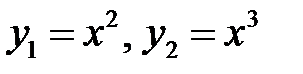 , и общее решение по-прежнему будет иметь вид
, и общее решение по-прежнему будет иметь вид
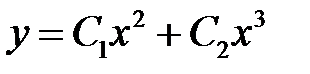 .
.
Пример 26. Решить уравнение 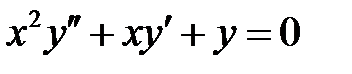 .
.
Решение. Запишем характеристическое уравнение и найдем его корни:
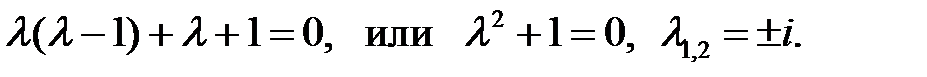
Общим решением преобразованного уравнения будет
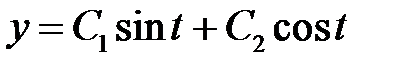
и, переходя к переменной 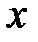 , получим общее решение исходного уравнения
, получим общее решение исходного уравнения
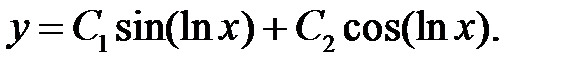
Пример 27. Решить уравнение 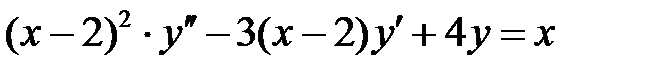 .
.
Решение. Сделаем замену независимой переменной по формуле 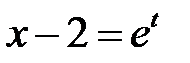 , тогда
, тогда
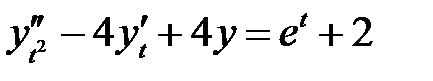 .
.
Характеристическое уравнение имеет корни 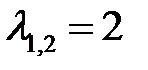 , следовательно, общее решение однородного уравнения
, следовательно, общее решение однородного уравнения
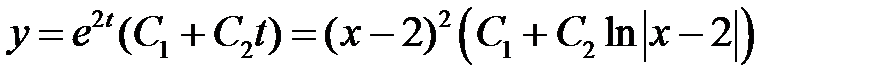 .
.
Правая часть неоднородного уравнения равна 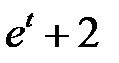 , поэтому следует искать частное решение по принципу суперпозиции в виде
, поэтому следует искать частное решение по принципу суперпозиции в виде 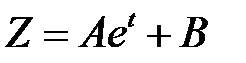 . Подставив в уравнение, получим
. Подставив в уравнение, получим 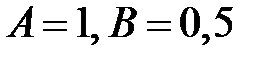 и
и
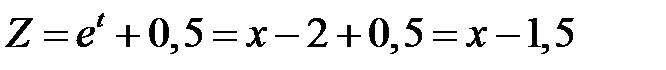 .
.
Следовательно, общее решение неоднородного уравнения
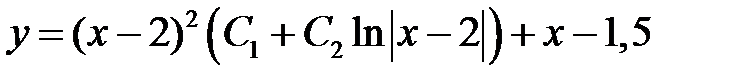 .
.
Пример 28. Составить линейное однородное дифференциальное уравнение (возможно меньшего порядка), имеющие частные решения 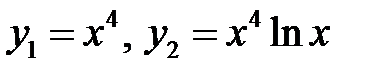 .
.
Решение. Очевидно, функции 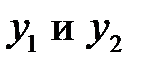 линейно независимые, следовательно, они могут быть фундаментальной системой решений линейного однородного уравнения второго порядка, которое может быть получено по формуле
линейно независимые, следовательно, они могут быть фундаментальной системой решений линейного однородного уравнения второго порядка, которое может быть получено по формуле
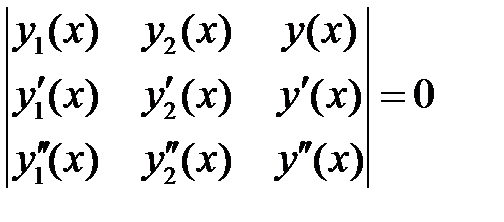 .
.
Заметим, что такие частные решения имеет уравнение Эйлера. Составим это уравнение. Корни характеристического уравнения кратные: 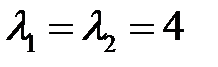 , следовательно, само уравнение имеет вид
, следовательно, само уравнение имеет вид
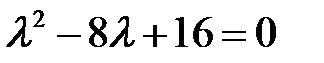 .
.
Этому уравнению соответствует промежуточное уравнение
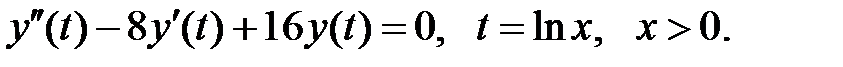
Переходя к переменной 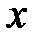 , получим уравнение Эйлера
, получим уравнение Эйлера
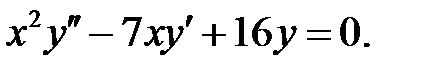
5.7. Краевые задачи
Для отыскания решения краевой задачи для линейного неоднородного уравнения 2 порядка с переменными коэффициентами
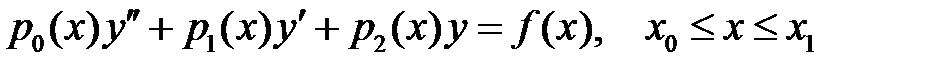 , (10)
, (10)
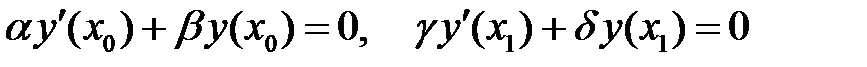 (11)
(11)
надо подставить общее решение уравнения (10) в краевые условия (11) и из этих условий определить, если это возможно, значения произвольных постоянных, входящих в формулу общего решения. В отличие от задачи с начальными условиями (задачи Коши), краевая задача не всегда разрешима, а если разрешима, то не обязательно единственным образом.
Пример 29. Найти решение уравнения 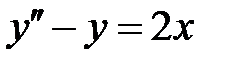 , удовлетворяющее краевым условиям
, удовлетворяющее краевым условиям 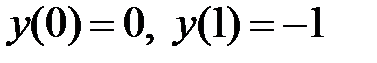 .
.
Решение. Подставляя общее решение
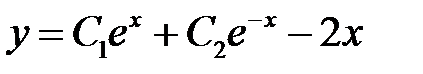
поочередно в краевые условия, получим
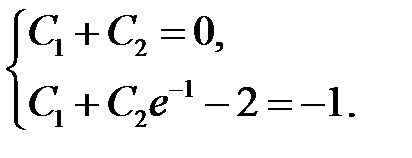
Откуда
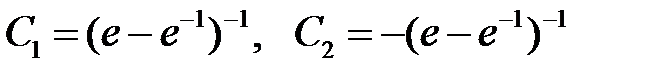 ,
,
так что искомым решением будет функция
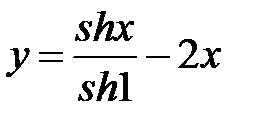 .
.
Пример 30. Решить краевую задачу
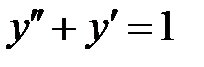 ,
, 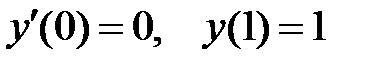 .
.
Решение. Общее решение данного уравнения
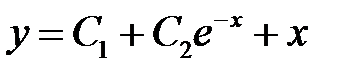 ,
,
отсюда 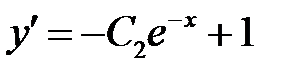 .
.
Учитывая краевые условия, получим для нахождения значений постоянных 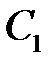 и
и 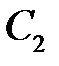 линейную систему
линейную систему
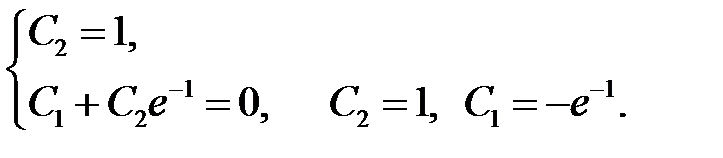
Поэтому искомым решением будет функция
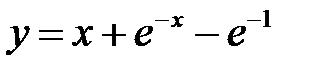 .
.
Пример 31. Решить краевую задачу
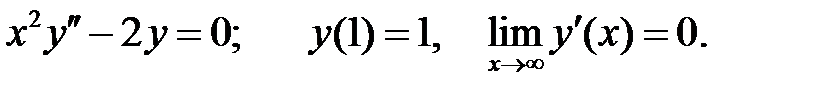
Решение. Общее решение данного уравнения имеет вид
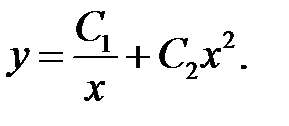
Выберем 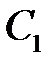 и
и 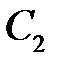 так, чтобы удовлетворялись краевые условия. Из условия
так, чтобы удовлетворялись краевые условия. Из условия 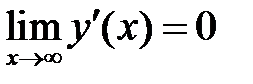 следует, что
следует, что 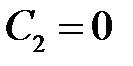 , а из условия
, а из условия 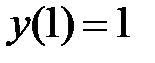 находим, что
находим, что 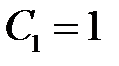 . Таким образом, указанная краевая задача имеет решение
. Таким образом, указанная краевая задача имеет решение 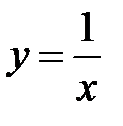 .
.
Функцией Грина краевой задачи (10), (11) называется функция 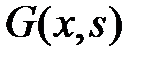 ,
, 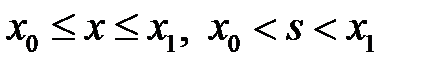 , при каждом фиксированном
, при каждом фиксированном 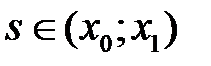 обладающая свойствами:
обладающая свойствами:
1) при 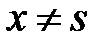
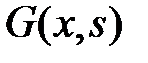 удовлетворяет уравнению
удовлетворяет уравнению
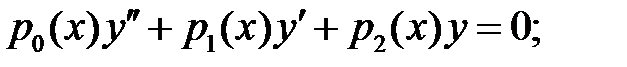 (12)
(12)
2) при 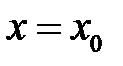 и
и 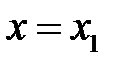
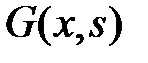 удовлетворяет заданным краевым условиям (11);
удовлетворяет заданным краевым условиям (11);
3) при 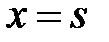
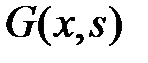 непрерывна по
непрерывна по 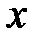 , а её производная по
, а её производная по 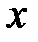 терпит разрыв первого рода со скачком, равным
терпит разрыв первого рода со скачком, равным 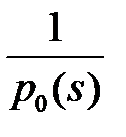 , т.е.
, т.е.
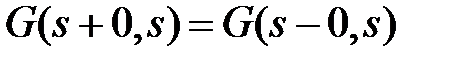 ,
, 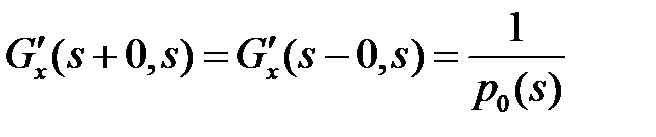 . (13)
. (13)
Чтобы найти функцию Грина краевой задачи (10), (11), надо найти два решения 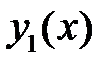 и
и 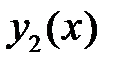 (отличные от
(отличные от 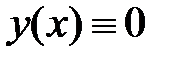 ) уравнения (12), удовлетворяющие соответственно первому и второму из краевых условий (11). Если
) уравнения (12), удовлетворяющие соответственно первому и второму из краевых условий (11). Если 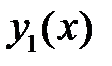 не удовлетворяет сразу обоим краевым условиям, то функция Грина существует и её можно искать в виде
не удовлетворяет сразу обоим краевым условиям, то функция Грина существует и её можно искать в виде
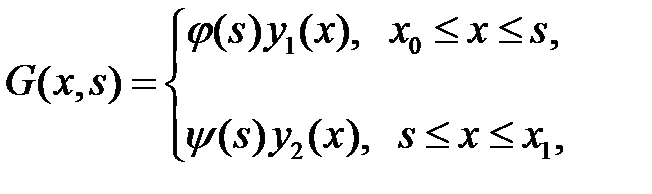
 (14)
(14)
где 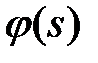 и
и 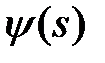 подбираются так, чтобы функция (14) удовлетворяла условиям (13), т.е. чтобы
подбираются так, чтобы функция (14) удовлетворяла условиям (13), т.е. чтобы
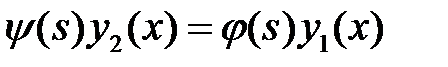 ,
, 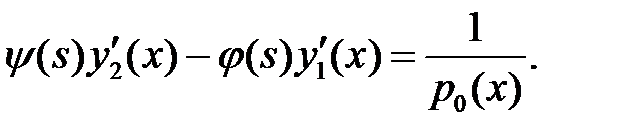 (15)
(15)
Если найдена функция Грина 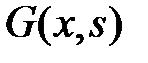 , то решение краевой задачи (10), (11) выражается формулой
, то решение краевой задачи (10), (11) выражается формулой
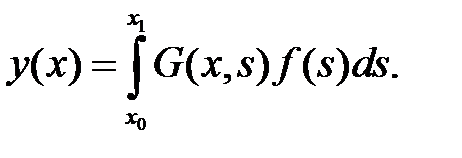
Пример 32. Построить функцию Грина для краевой задачи
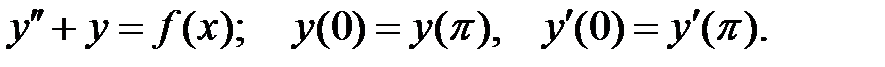
Решение. Общее решение уравнения 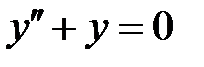 есть
есть 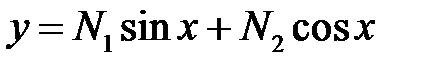 . Подберем постоянные
. Подберем постоянные 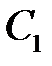 ,
, 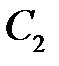 ,
, 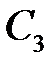 ,
, 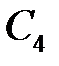 так, чтобы выполнялись краевые условия. Отсюда при
так, чтобы выполнялись краевые условия. Отсюда при 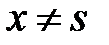 имеем
имеем
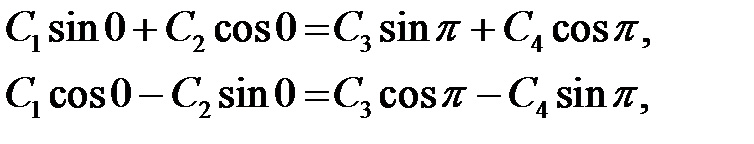
и
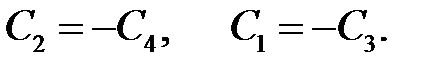 (*)
(*)
Из непрерывности 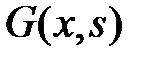 при
при 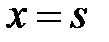 , а также скачка производной
, а также скачка производной 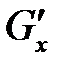 при
при 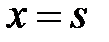
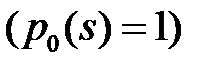 следуют соотношения
следуют соотношения
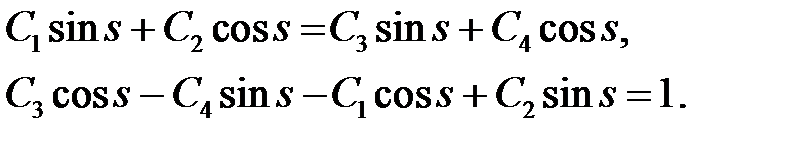 (**)
(**)
Из системы (*) и (**) находим

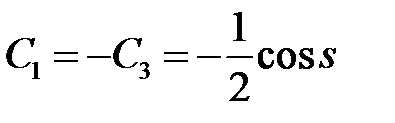 ,
, 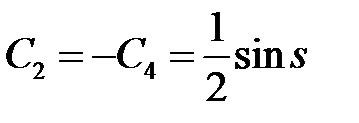 .
.
Таким образом, выбирая 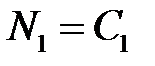 и
и 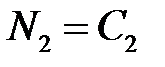 , получаем
, получаем
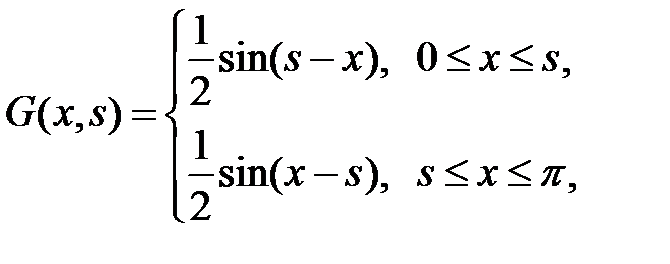
или 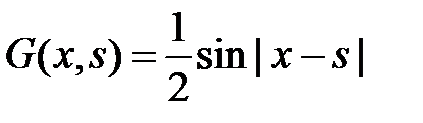 при
при 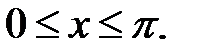
5.8. Индивидуальные задания








