Контрольные вопросы.
1. Дайте определение комплексного числа.
2. Какие числа называются комплексно – сопряженными?
3. Какие комплексные числа называются равными?
4. Как вычислить модуль комплексного числа?
5. Как производятся действия над комплексными числами в алгебраической форме?
Краткие теоретические сведения.
Для всякого комплексного числа z = a + ib справедливо равенство:
z = R ( cosφ + isinφ ) называют тригонометрической формой комплексного числа,
z = 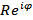 – называют п оказательной формой комплексного числа
– называют п оказательной формой комплексного числа
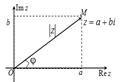 Здесь
Здесь 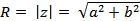 - модуль комплексного числа - расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора.
- модуль комплексного числа - расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора.
Угол φ между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке, называется аргументом комплексного числа - 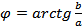 .
.
Действия над комплексными числами в тригонометрической форме.
| В тригонометрической форме z 1 = R 1 ( cosφ 1 + isinφ 1 ), z 2 = R 2 ( cosφ 2 + isinφ 2 ) | В показательной форме
Z1 = 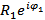 , Z2 = , Z2 = 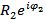
| |
| Умножение | Z1 ∙ Z2 = R1∙R2(cos(φ1+φ2) + isin(φ1+φ2)). | Z1·Z2= 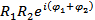
|
| Деление | 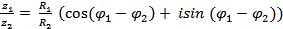 . .
| 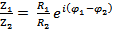 , ,
|
| Возведение в степень | zn =Rn(cos nφ + isin nφ) - формула Муавра | 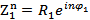 . .
|
| Извлечение корня | 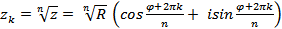 , k = 0,1,2.....n-1 , k = 0,1,2.....n-1
| 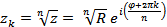 ,
k = 0,1,2.....n-1 ,
k = 0,1,2.....n-1
|
Примеры решения задач:
Пример. А) Представить числа z1 = 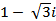 ,
, 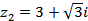 в тригонометрической и показательной форме,
в тригонометрической и показательной форме,
Б) вычислить в тригонометрической форме: 1) z1∙z2; 2) 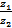 ; 3)
; 3) 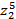 ; 4)
; 4) 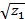
Решение: А). Получим тригонометрическую и показательную форму z1 = 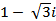 ,
,
1) Найдем модуль числа - 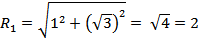 , 2) Найдем аргумент числа -
, 2) Найдем аргумент числа - 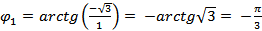 ,
,
3) запишем к.ч. в тригонометрической и показательной форме:
z1 = 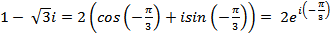 .
.
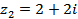 ,
,
1) 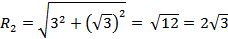 - модуль числа,
- модуль числа,
2) 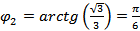 - аргумент числа
- аргумент числа
3) запишем к.ч. в тригонометрической и показательной форме:
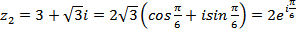 .
.
Б) Произведение:
z1∙z2 = 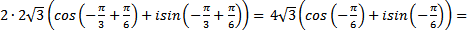
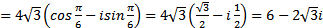 .
.
Частное:
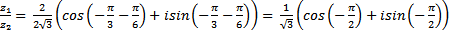 =
=
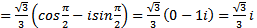 .
.
Возведение в степень:
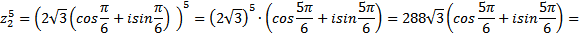
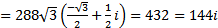 .
.
Извлечение из под знака корня:
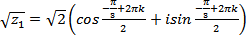 .
.
Пр k=0: 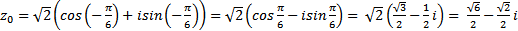 ;
;
Пр k=1: 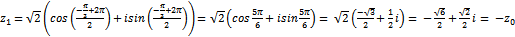 .
.








