Тема: « Действия над комплексными числами »
Цель работы: научиться выполнять действия над комплексными числами в алгебраической форме, решать квадратные уравнения с отрицательным дискриминантом.
Краткие теоретические сведения.
Комплексные числа - числа вида Z = a + ib, где a,b – вещественные числа, а i =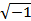 
- мнимая единица (i2 = −1). Множество комплексных чисел обозначается C.
Действительные числа a и b комплексного числа Z = a + ib, называются действительной и мнимой частью числа z и обозначаются, соответственно, Rez=x и Imz=y.
Два комплексных числа z1=a + ib и z2=c + id называются равными в том и только том случае, если a = c, b = d.
Запись Z=a + ib называют алгебраической формой комплексного числа z.
Числа Z=a + ib и 
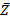=a − ib называют комплексно сопряженными.
Геометрическое представление комплексного числа
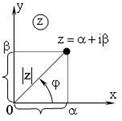
Если рассмотреть плоскость с прямоугольной системой координат, то любому комплексному числу z = a + ib можно сопоставить точку на этой плоскости с соответствующими координатами (a;b), и радиус-вектор R комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу (рис. 1). Данная плоскость называется комплексной. Действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.
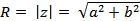- модуль комплексного числа - расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора.
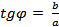, где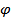 
- аргумент комплексного числа.
Действия над комплексными числами в алгебраической форме.
Сложение: Z1 + Z2 = (a+ib) + (c+id) = (a+c) + (b+d)i.
Вычитание: Z1 - Z2 = (a+ib) - (c+id) = (a-c) + (b-d)i.
Умножение: Z1 · Z2 = (a+ib)(c+id)=(ac − bd) + (ad + cb)i.
Деление: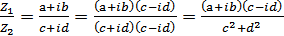 
.
Умножение на сопряженное:
Z ·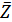 
=( a + bi )( a - bi )= a 2 – b 2 i 2 = a 2 – b 2 ·(-1) = a 2 + b 2 – квадрат суммы
Примеры решения задач:
Пример 1. Выполнить действия над комплексными числами, представив результат в алгебраической форме:
Z1 = 4+ 5i, Z2 = 6−9i.
Решение: 1) Z1 + Z2 = (4+ 5i) + (6−9i)= 4+6+5i -9i .= 10 – 4i
2) Z1 - Z2 = (4+ 5i) - (6−9i)= 4-6+5i +9i .= -2 + 14i
3) Z1 ·Z2 = (4+5i)(6− 9i)= 24 −36i + 30i− 45i2= 24 -6i - 45·(-1) = 69 -6i.
4) 
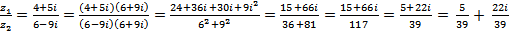
Ответ: Z1 + Z2 =10 – 4i, Z1 - Z2 = -2 + 14i, Z1 ·Z2 =69 -6i,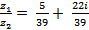 
Пример 2. Раскрыть скобки, используя формулы сокращенного умножения:
1) (2+ 3i)2 = 22 + 2·2·3i + (3i)2 = 4 +12i + 9·(-1) = -5+12i,
2) (5 + 4i)(5 - 4i)= 52 –42i2= 25 – 16·(-1) = 25 + 16 =4,
3) (3-5i)2 = 32 - 2·3·5i + (-5i)2 = 9 - 30i + 25(-1) = -16- 30i.
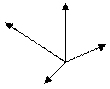
Пример 3. Изобразим на комплексной плоскости числа
Z1 = 2 + i; Z2 = 3i;
Z3 = -3 + 2i; Z4 = -1 – i.