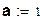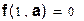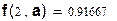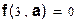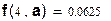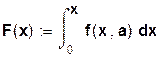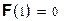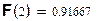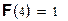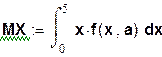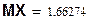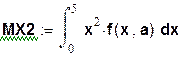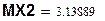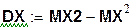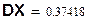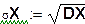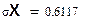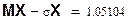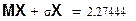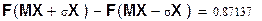ИДЗ ТВ-3 по теме « Дискретная и Непрерывная Случайная Величины»
Задание.
I ] ДСВ
1) На заданном случайном эксперименте определить ДСВ и построить её мат. модель.
2) Определить функцию распределения и изобразить схематически графики функции и ряда
распределения ДСВ.
3) Определить и вычислить математическое ожидание , дисперсию и СКО ДСВ.
4) Вычислить вероятность P(|X-MX| ≤ σX).
Рекомендация: результаты вычислений представить в виде таблицы
| x i | (x i )2 | P(x i ) | F( x≤ x i ) |
| x1 | |||
| ……. | |||
| x n | |||
| x>x n | - | - | |
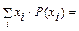
| 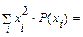
| 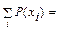
|
II] НСВ
1) Определить заданную функцию как плотность распределения НСВ; параметр определить из условие нормировки.
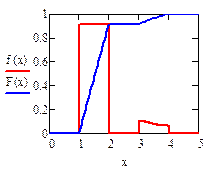
2) Определить и записать явный вид функции распределения НСВ; (изобразить схематически ее графики плотности и функции НСВ).
3) Определить и вычислить числовые характеристики НСВ.
4) Вычислить вероятность P(|X-MX|≤σX)
| 11∙12∙13∙04ДСВ Задача 1: За каждую из последовательно предлагаемых 4 задач, которые конкурсант может решить с вероятностями 0.9, 0.8, 0,7,0.6, начисляется 1 балл. Если задача не решена, конкурс прекращается. СВ Х- количество набранных конкурсантом баллов.
è1) В ведём обозначения: «1i»/ «0 i » - i- задача решена/ не решена. Мат. модель ДСВ:
Х={0,1,2,3,4} ó "01"; "11∙02"; "11∙12∙03”; "11∙12∙13∙04"; "11∙12∙13∙14" PX= { 0.1; 0.9*0.2; o.9*0.8* 0.3; 0.9*0.8*0.7*0.4; 0.9*0.8*0.7*0.6 } |
2) Функция распределения ДСВ: 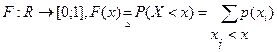
3) Математическое ожидание ДСВ: 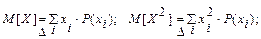
Дисперсия ДСВ: 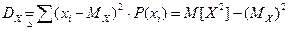 ; СКО ДСВ:
; СКО ДСВ: 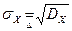
| x i | (x i )2 | P(x i ) | F(x i ) | |
| 0 | 0 | 0.1 | 0 | |
| 1 | 1 | 0.18 | 0.1 | |
| 2 | 4 | 0.216 | 0.28 | |
| 3 | 9 | 0.2016 | 0.496 | |
| 4 | 16 | 0.3024 | 0.6976 | |
| >4 | 1.000 | |||
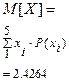
| 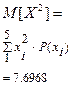
| 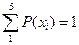
|
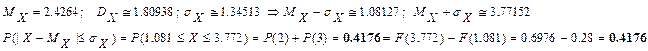
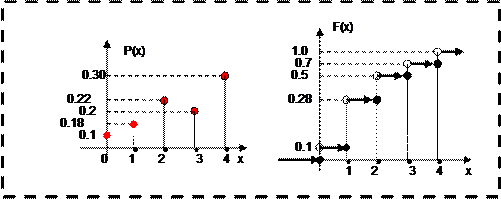
Результаты.
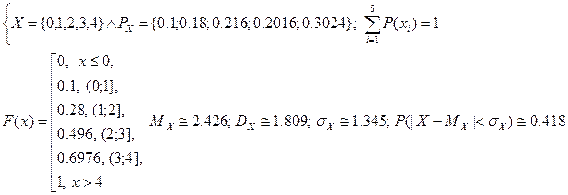
НСВ 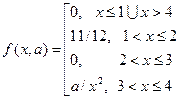
1) Определим заданную функцию f ( x , a ) как плотность распределения НСВ :
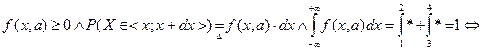 a=1
a=1
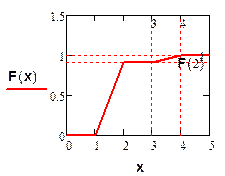
2) Функция распределения НСВ: 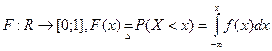
3) 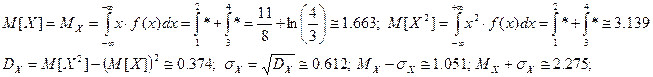 ;
;
|
|
|
|
4) 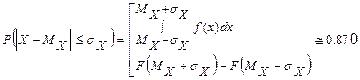
НСВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) Определим заданную функцию f ( x , a ) как плотность распределения НСВ :
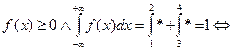 a=1
a=1
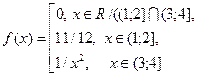 è
è 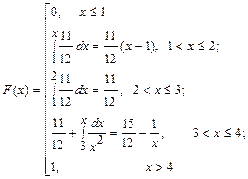
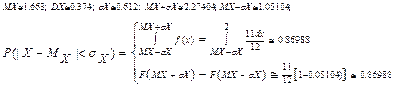









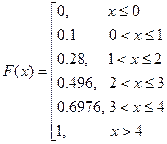
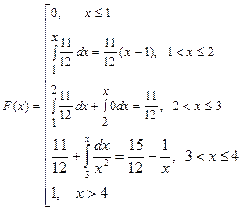
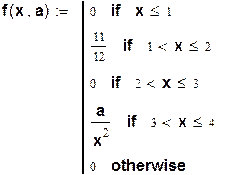
 11/12=0.91(6)
11/12=0.91(6)