Вариант направления ж.д. линии, у которого все значения частных критериев эффективности наилучшие (максимальные или минимальные соответственно), называется «абсолютным рекордистом »[51].
При многокритериальном выборе варианта направления ж.-д. линии по методу идеальной точки необходимо определить «расстояние» в многомерной (m-мерной) системе координат от реальных вариантов направлений, намеченных Вами по карте (xi, i=1, …n), до идеального варианта (идеальной точки в m-мерном пространстве частных критериев эффективности, того самого воображаемого “абсолютного рекордиста”). Идеальная точка, к которой каждый из вариантов “мечтает приблизиться”, расположена в начале координат m-мерного критериального пространства, т.е. нормализованные значения всех частных критериев для идеального варианта равны нулю, формально: rjидеал = 0, для всех j=1, …m.
Итак, нам необходимо определить «расстояние» до идеальной точки в m-мерном критериальном пространстве. Для этого рассчитаем для каждого сравниваемого i – того варианта направления величину ρ i , i=1,…n по формуле из работы /7, с.10, формула (5)/
ρ i = [ ∑ (cj · (rji )2) ]1/2 , для всех j=1, …m , (П1.3)
где cj – весовые коэффициенты частных критериев эффективности,
учитывающие “вес” – значимость каждого критерия в
общей оценке варианта направления ж.-д. линии;
безразмерные, причем должно выполняться условие
∑ cj = 1, j=1, …m, при 0‹ cj ‹ 1. (П1.4)
Таким образом, идея метода идеальной точки состоит в предположении, что чем ближе реальный вариант направления xi к идеальному варианту x идеал (в общем случае – недостижимому), тем лучше этот i-тый вариант, т.е., чем меньше ρ i - тем лучше вариант направления.
Следовательно, критерий ρ i , вычисляемый уже через нормированные значения частных критериев эффективности rji, является глобальным (основным, обобщенным, главным) критерием эффективности вариантов направлений.
Следует сделать замечание о введенных нами в формуле (П1.3) весовых коэффициентах частных критериев cj , которые иногда называют также шкалирующими коэффициентами, рангами или просто весами критериев. Наше замечание касается не той цели, которую преследуют во многих методах решения многокритериальных задач выбора, вводя подобные веса критериев[52] , но методам определения значений этих весов. Дело в том, что по результатам многочисленных исследований (см. работы /16/, /17/, /18/, /19/, /20/) ЛПР часто дает противоречивую прямую оценку весов критериев, допускает непоследовательность в расставленных приоритетах целей и др. Поэтому наиболее последовательно и обоснованно данную задачу (определения рангов или весов критериев) можно решить лишь с применением теории полезности (через определение точек равноценности, см. /3/, /4/, /21/, а также часть 6 пособия).
Однако в курсовом проекте, ввиду недостатка времени для решения подобной задачи, а также необходимости уделить большее внимание именно вопросам трассирования вариантов – проектированию их планов и профилей, мы допускаем непосредственное – прямое назначение весов частных критериев эффективности, так сказать, назначение cj по интуиции, но обязательно с письменным обоснованием принятых Вами cj в пояснительной записке, а также с соблюдением условия (П1.4).
Заметим также, что и вид условия (П1.4) неявно предполагает справедливость аддитивной функции полезности (ценности), хотя непосредственно установление справедливости такого предположения для ЛПР в задаче многокритериального выбора по методу идеальной точки – не производится.
Далее рассмотрим пример сравнения вариантов принципиальных направлений проектируемой ж.-д. линии при многих критериях по методу идеальной точки, которым Вы можете воспользоваться, если перед Вами будет стоять подобная задача. Подробнее о методе идеальной точки Вы можете прочитать в работе /15/.
Пример сравнения вариантов направления проектируемой
ж.-д. линии при многих критериях по методу идеальной точки
Дано: топографическая карта, на которой просматриваются несколько конкурентных принципиальных направлений проектируемой ж.-д. линии (водораздельное, косогорное, долинное) – см. рис. П1.1; описание района проектирования (река Светлая – судоходная II класса); расчетные размеры перевозок для проектируемой ж.-д. линии на перспективу (линия высокой категории – I); два руководящих уклона ip1 =11 ‰ (равен уклону линии примыкания) и ip2 =9 ‰ .
Требуется: выбрать два (может получиться - одно) принципиальных конкурентных направления проектируемой ж.-д. линии, по которым наиболее эффективно пройти различными значениями руководящих уклонов; обосновать свой выбор.
Решение.
1. На рис. П1.1 намечаем три принципиальных направления ж.-д. линии: водораздельное, косогорное, долинное. По каждому из этих трех направлений можно пройти уклонами ip1 =11 ‰ и
ip2 =9 ‰. Следовательно, всего возможны шесть вариантов
направления ж.-д. линии, см. рис. П1.1.
По всем трем направлениям сначала прокладывается магистральный ход[53] с руководящим уклоном, равным уклону линии примыкания, т.е. с ip1 =11 ‰, а затем пробуется второй заданный уклон ip2 =9 ‰.
Итак, в нашей задаче будет шесть вариантов.
Первый вариант - уклоном ip1 =11 ‰ по водораздельному направлению – альтернатива х1 (с тоннельным пересечением отрогов главного хребта, длина тоннеля около 5 км).
Второй вариант – уклоном ip2 =9 ‰ по водораздельному направлению – альтернатива х2 (без тоннельного пересечения, но с дополнительным развитием линии по главному водоразделу и его склонам).
Третий вариант – уклоном ip1 =11‰ по косогорному направлению – альтернатива х3 (максимально приближается к геодезической линии L0).
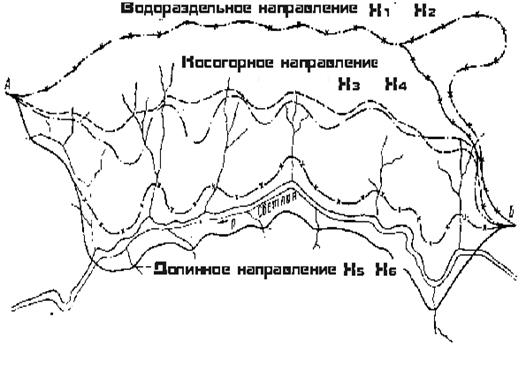 |
Рис. П1.1. Варианты конкурентных принципиальных направлений проектируемой ж.-д. линии А – Б (показаны магистральные ходы по направлениям, а не трассы, т.е. без вписывания кривых и т.д.), топографическая карта масштаба 1 : 500 000 (при издании пособия линейные размеры были искажены, горизонтали не показаны)
Четвертый вариант – уклоном ip2 =9 ‰ по косогорному направлению – альтернатива х4 (по замыслу – как третий вариант, но с большим развитием линии, из-за меньшей величины уклона необходимо глубже вписываться в боковые долины притоков реки Светлая).
Пятый вариант – уклоном ip1 =11 ‰ по долинному направлению – альтернатива х5 (учитывая тот факт, что правый склон долины реки Светлая более крутой, но не заболочен, пятый вариант проходит по правому склону, пересекая значительное число участков склона неблагоприятных в инженерно-геологическом отношении, при необходимости вписываясь в боковые долины притоков).
Шестой вариант – уклоном ip2 =9 ‰ по долинному направлению – альтернатива х6 (руководящий уклон по шестому варианту более пологий, чем по пятому варианту, поэтому для того, чтобы обеспечить приемлемые объемы земляных работ и не удлинять линию чрезмерно, пришлось пройти по левому склону долины реки Светлая – более пологому, но заболоченному и, кроме того, предусмотреть два больших мостовых перехода, длиной более 500 м каждый, через реку Светлая).
2. Назначаем частные критерии эфективности Rj , j=1, …m[54].
Строго говоря, количество частных критериев эффективности не ограничено, однако, в соответствии с проведенными исследованиями (см., например, работу /17/), не рекомендуется использовать более 9 критериев.
В нашем примере ЛПР[55] назначил семь частных критериев эффективности Rj , j=1, …7 . Ниже приведены описания всех семи частных критериев с кратким обоснованием их применения и направлением оптимизации.
è R1 – длина направления, км (определена примерно по карте путем укладки магистрального хода); обоснование критерия : критерий позволяет в первом приближении определить длину будущей трассы по каждому направлению, что очень важно для ж.-д. линии I категории, т.к. каждый «лишний» километр будущей трассы приведет к «лишним» тонно-километрам грузооборота; направление оптимизации: желательно минимизировать.
è R2 – сумма преодолеваемых высот в обе стороны (туда+обратно), м (определена примерно по магистральному ходу – по фиксированным точкам, разумеется по “земле”, т.е. без проектирования проектной линии продольного профиля); обоснование критерия : критерий дает возможность косвенно оценить величины эксплуатационных расходов – через механическую работу локомотива и сил сопротивления, через расход топлива (электроэнергии) и время хода и т.д.; направление оптимизации: желательно минимизировать.








