Пример решения задачи.

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Для желающих

повысить свой уровень по технической механике – ещё один вариант задачи по этой теме, более сложный. Зачтётся при подведении итогов – выполнение до 05.04.2020.

Варианты заданий – стр.86, свой вариант по списку студентов в группе

Учебник В.И.Сеткова, «Сборник задач по технической механике», пример 18, стр. 81.

Пример выполнения задания. Решение задач на определение линейных и угловых перемещений при поперечном изгибе статически определимых балок методом Мора с применением правила Верещагина.

Определить горизонтальное перемещение точки А. (с.82С\т). Для определения жёсткости ЕJ материал – сталь марки Ст3, а сечение – двутавровая балка № 18. Модуль продольной упругости Е = 2,1• 10⁵ МПа

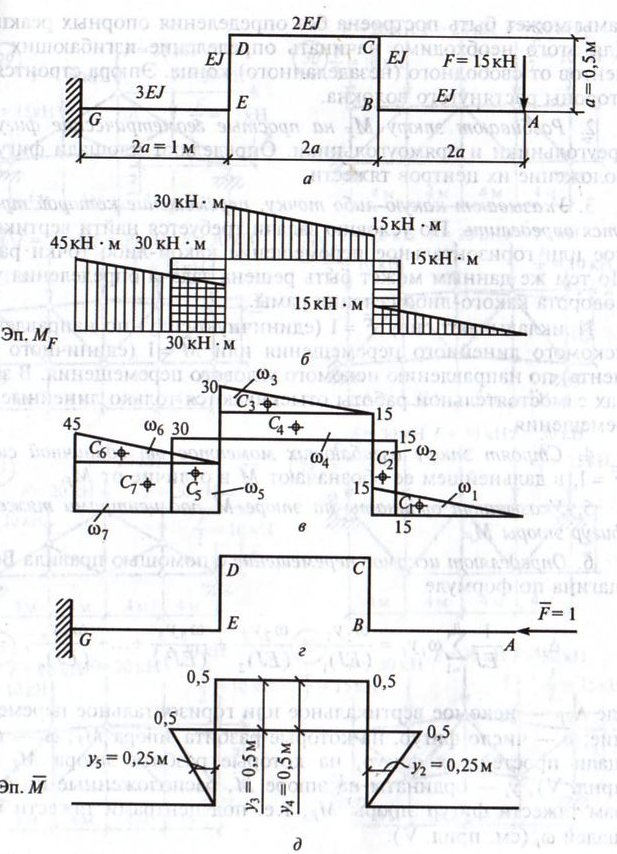
Решение.

1. Определим изгибающие моменты в характерных точках от силы F = 15кН

А) Элемент АВ

М_А = 0

М_в= - F•2а = -15•2•0,5 = -15 кН•м

Б) Элемент ВС

М_в = 0 М_в= - F•2а = -15•2•0,5 = -15 кН•м

М_с= 0 М_c= - F•2а = -15•2•0,5 = -15 кН•м

В) Элемент С D

М_c = 0 М_c= - F•2а = -15•2•0,5 = -15 кН•м

М_D = 0 М_D= - F•4а = -15•4•0,5 = -30 кН•м

Г) Элемент D Е

М_D = 0 М_D= - F•4а = -15•4•0,5 = -30 кН•м

М_Е= 0 М_Е= - F•4а = -15•4•0,5 = -30 кН•м

Г) Элемент Е G

М_Е= 0 М_Е= - F•4а = -15•4•0,5 = - 30 кН•м

М_G= 0 М_G= - F•5а = -15•5•0,5 = - 45 кН•м

По найденным значениям строим эпюру М _F ( C .82,б)

2. Разбиваем эпюру М _F на простейшие фигуры (C.82,в). Эпюра М_F разбита на 7 частей: 3 треугольника и 4 прямоугольника. Найдём их площади:

W₁ = 0,5 •1м •15 кН•м= 7,5 кН•м²

W₂= 0,5м •15 кН•м= 7,5 кН•м²

W₃= 0,5 •1м •15 кН•м= 7,5 кН•м²

W₄= 1м •15 кН•м= 15 кН•м²

W₅= 0,5м •30 кН•м= 15 кН•м²

W₆ = 0,5 •1м •15 кН•м= 7,5 кН•м²

W₇= 1м •30 кН•м= 30 кН•м²

Укажем центры тяжести каждой из фигур: С₁ С₂ С₃ С₄ С₅ С₆ С₇

3. По условию задачи требуется найти горизонтальное перемещение точки А. Прикладываем единичную силу (вектор) F = 1 в точке А и направляем её горизонтально (по направлению искомого перемещения). Направление действия силы принимается произвольно (C .82,г)

4. Определим изгибающие моменты в характерных точках от силы F ¯=1

А) Элемент АВ

¯М_А =¯М_B = 0

Б) Элемент ВС

¯М_B = 0

¯М_C = - F•а = - 1• 0,5 = - 0,5м

В) Элемент D Е

¯М_D = - F•а = - 1• 0,5 = - 0,5м

¯М_E = 0

Г) Элемент Е G

¯М_E =¯М_G = 0

По найденным значениям строим эпюру ¯М

5. По приложению V (c.218), укажем ординаты на эпюре М¯ под центрами тяжести эпюр М_F(площадей w_i)

у₁ = 0, т.к эпюры М на участке АВ нет.

у ₂ = 0,25 т.к.:

- С₂ расположен в середине участка ВС (на эпюре «в» – по прил. V)

- далее смотрим на эпюре «д» - эта середина соответствует 0,25

у ₃ = у ₄ = 0,5

- на участке DC – C₃ расположена на 1\3, C₄ посередине (на эпюре «в»)

- на эпюре «д» - постоянная величина 0,5

у ₅= 0,25 (аналогично у ₂)

у₆ = у₇ = 0, т.к эпюры М на участке EG нет.

6. Определим искомое перемещение по правилу Верещагина

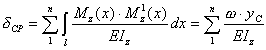Δ

Δ_iF = w₁• у₁\EJ + w₂• у₂\EJ + w₃• у₃\2EJ + w₄• у₄\2EJ + w₅• у₅\EJ+ w₆• у₆\3EJ+ w₇• у₇\3EJ

Δ_iF = 0 + 7,5•0,25\ EJ + 7,5•0,5\ 2EJ + 15•0,5\ 2EJ + 15•0,25\ EJ + 0 + 0 =

0 + 1,875\ EJ + 1,875\ 2EJ + 3,75 \ 2EJ + 3,75\ EJ + 0 + 0 = 11,25\ EJ

Для двутавровой балки № 18 момент инерции J_x = 1290 cм⁴, сталь марки Ст3, Е = 2,1• 10⁵ МПа.

Δ_iF = Δ_А ^гор =11,25• 10³ МН•м³\1290•10^-8 м⁴•2,1•10⁵МПа = 0,0042м = 0,42 см

Ответ: Δ_А ^гор = 0,42 см.

Обратная связь осуществляется :

8 912 669 76 26,

эл.почта teslia@uralweb.ru ,

группа в Контакте Строители колледж,

WhatsApp по телефону 8 953 821 01 05

Рекомендации

Задача простая, своих формул не изобретаем, всё по примеру.