Линейные преобразования стационарных случайных процессов
На практике часто приходится решать задачи типа : имеется некоторая система
S, на вход которой поступает сигнал X(t) . В результате преобразования входного сигнала системой S на ее выходе появляется с.п. Y(t), который называется “откли-
ком” или “реакцией системы” на входной сигнал X(t). Символичеки преобразова-
ние случайного поцесса X(t) в сигнал Y(t) системой S записывают в виде
Y(t) = P[X(t)] ,
здесь символ Р играет роль оператора преобразования . Среди множества всех
возможных операторов будем рассматривать только линейные однородные операторы L [ · ].
Определение: Оператор L [ · ] называется линейным однородным, если он
обладает свойствами:
1) линейный однородный оператор от суммы функций равен
сумме линейных однородных операторов от каждой функции
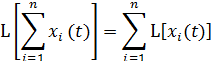
2) постоянную величину можно выносить за знак оператора L
L [ c×x(t) ] = c× L [ x(t) ] .
К линейным однородным операторам относятся операторы:
1) оператор дифференцирования у(t) = dx(t)/ dt ;
t
2) оператор интегрирования у(t) = a(t)× ò x(t) dt ;
0
3) оператор интегрирования с определенным весом u(t)
t
y(t) = ò u(t)×x(t) dt ;
0
4) оператор дифференциального уравнения второго порядка
у(t) = a2 · d2x(t)/ dt2 + a1· dx(t)/ dt + a0×x(t) .
Рассмотрим применение некоторых указанных операторов к стационарным случайным процессам.
Пример 12. Пусть X(t) - стационарный в широком смысле с.п. , для которого
математическое ожидание M[X(t)] = mx и ковариационная функция
Kx(t) известны.
Найти характеристики с.п. на выходе системы, заданной :
1. оператором дифференцирования;
2. оператором интегрирования.
Решение. 1. Используя формулу (25) получим
M[Y(t)] = my(t) = dmx/dt = 0
Вычисление корреляционной функции с.п. Y(t) производится по формуле
Ky(t) = - ¶2 Kx(t) / ¶t2.
Тогда спектральная плотность мощности процесса Y(t) будет
¥
Sу(w) = ò e- i w t (- ¶2 Kx(t)/ ¶t2 ) dt =
- ¥
∞ ∞
= ò e- i w t [ - ¶2 ( ò Sx(w) ei w t dw )/ ¶t2 ] dt =
-¥ -¥
¥ ¥
= ò w2 e- i w t ( ò Sx(w) ei w t dw) dt =
-¥ -¥
¥
= w2 ×ò Kx(t) e- i w t dt = w2 Sx(w) .
-¥
Таким образом спектральные плотности мощности сигнала X(t) и его производной Y(t) связаны соотношением
Sy(w) = w2 Sx(w). (48)
t
2. Рассмотрим оператор интегрирования Y(t) = ò X(t)dt.
0
Характеристики процесса Y(t) будут
t
M [ Y(t)] = ò mx×dt = mx×t ;
0
t1 t2 t2 t1
Ky(t1,t2) = ò ò Kx(s1,s2) ds1 ds2 = ò (t2 -t) Kx(t) dt + ò (t1-t)Kx(-t)dt =
0 0 0 0
t2- t1
= ò (t2-t1-t)Kx(t)dt. (49)
0
Полагая t1= t2 = t получим расчетное выражение для дисперсии
t t t
Dy(t) = ò (t-t)Kx(t)dt + ò (t-t)Kx(-t)dt = ò (t-t)[Kx(t)+ Kx(-t)]dt =
0 0 0
t
= 2 ò (t-t)Kx(t)dt . (53)
0
Пример 13. Стационарный случайный процесс X(t) имеет
корреляционную функцию Kx(t) = sx2 e-2l½t½. Определить
дисперсию случайного процесса
t
Y(t) = ò X(t)dt .
0
Решение. Применим формулу (50) и найдем
t t
D[Y(t)] = 2 ò (t-t)Kx(t)dt = 2sx2 ò (t-t)×e-2lt dt =
0 0
t t
= 2sx2 [ ò t× e-2lt dt - ò t× e-2lt dt ] =
0 0
t t
= 2sx2 [ t× (- 1/ 2l)× e-2lt½ + (1/ 2l) ò t d(e-2lt)] =
0
t t
= 2sx2 [(-t/ 2l)( e-2lt -1) + (1/ 2l)(t× e-2lt ½ - ò e-2lt dt)] =
0 0
sx2
= ¾ [ 2lt -1 + (1+ 2lt -2l)× e-2lt ]/ 2l2 .
2l2
Из полученного выражения и формулы (50) следует, что интеграл от стационарной случайной функции свойством стационарности не обладает.ð
Потоки событий
Потоком событий называется последовательность событий, происходя-
щих в случайные моменты времени. Примеры: поток вызовов, поступаю-
щих на телефонную станцию; поток почтовых отправлений на почте; поток
шайб, забитых при игре в хоккей и т.д.
В общем случае поток событий представляет собой последовательность
случайных точек t1, t2, ... , tn, ... на оси времени с разделяющими их случай-
ными интервалами T1, T2, ... , Tn = tn+1 - tn ( рис. 21).
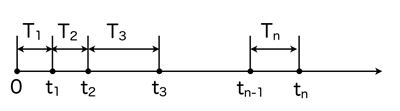
рис.21
Потоки событий отличаются друг от друга законами распределения интервалов T1, T2, ... , их зависимостью или независимостью между собой.
Важными характеристиками потоков является их ординарность, отсутст-
вие последействия, стационарность.
1. Ординарность. Поток событий называется ординарным, если события в нем
появляются поодиночке, а не группами.
Это означает, что вероятность попадания на участок времени D t двух и более событий очень мала по сравнению с вероятностью попадания на него ровно одного события.
Если обозначить р1(t, D t ) вероятность попадания на участок (t, t + D t ) ровно одного события, р 0 (t, D t ) вероятность непопадания на него ни одного события и р˃1(t, D t ) - вероятность попадания на него двух и более событий, то очевидно следующее равенство
р1(t, D t ) + р 0 (t, D t ) + р˃1(t, D t ) = 1.
Важной характеристикой потоков событий является интенсивность потока.
Обозначим Х (t, D t ) случайное число событий, попадающих на элементарный участок (t, t + D t ), для ординарного потока событий.
Интенсивностью ( плотностью) ординарного потока событий в момент t называется величина
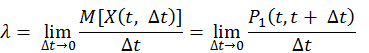 ,
,
если данный предел существует.
Физический смысл интенсивности потока событий - это среднее число событий, приходящихся на единицу времени для элементарного участка (t, t + D t).
Среднее число событий ординарного потока, приходящееся на интервал
(t, t + τ ) равно
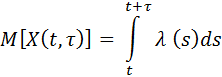
и при постоянной интенсивности потока λ( t ) = λ будем иметь
M [X ( t, τ )] = λτ .
2. Отсутствие последействия.
Поток событий называется потоком без последействия, если для любых
Неперекрывающихся участков времени τ 1 , τ 2 , …, τ n числа событий
X 1 = X ( t 1 , τ 1 ), X 2 = Х( t 2 , τ 2 ),…, Xn = Х( t n , τ n ), попадающих на эти участки, представляют собой независимые случайные величины.
Если поток без последействия, ординарен и имеет постоянную интенсивность λ, то число событий Х( t , τ ) , попадающих на участок времени τ, имеет распределение Пуассона с параметром α = λτ.
Ординарный поток событий, в котором отсутствует последействие,
называется пуассоновским потоком .
Для пуассоновского потока вероятность наступления за время t ровно m
событий определяется формулой
(α) m
Р(m) = ¾¾¾ × e - α ,
m!
а функция распределения F(t) = P(T < t) интервала Т между соседними событиями является показательной
F(t) = 1 - e - l t (t > 0).
3. Стационарность.
Поток событий называется стационарным, если все его вероятностные характеристики не меняются со временем.
Для стационарного потока событий вероятность попадания того или иного числа событий на участок длины τ зависит только от длины этого участка и не зависит от того, где именно на оси времени этот участок расположен . Это значит, что числа событий Х(t 1,τ ) и Х(t 2,τ ), попадающих на два участка одинаковой длины τ, будут иметь одинаковое распределение. Отсюда следует, что для стационарного потока событий его интенсивность λ( t ) есть величина постоянная: λ( t ) = λ = const.
Поток событий, обладающий всеми тремя свойствами, называется
простейшим потоком (или стационарным пуассоновским потоком).
Более сложным потоком событий, по сравнению с простейшим, является поток с ограниченным последействием. Так будем называть поток, у которого случайные интервалы Т 1, Т 2, … между событиями представляют собой последовательность независимых одинаково распределенных случайных величин.
Стационарный поток событий с ограниченным последействием называется потоком Пальма. Для такого потока событий интервалы Т 1, Т 2, … между соседними по времени событиями представляют собой независимые случайные величины.
Потоки Пальма широко применяются в теории восстановления – разделе теории надежности технических устройств.
Марковские процессы
Предположим, что физическая система может находится в одном из дис -
кретных состояний S1, S2, ..., Sn и переходить в определенные моменты вре -
мени tk (шаги) из одного состояния в другое. Например, прибор может на - ходиться в следующих состояниях: S1 - исправен; S2 - неисправен; S3 - cпи -
сан в отход; S4 - находиться в ремонте и в дальнейшем может вернуться в
эксплуатацию или быть списанным, если его ремонт невозможен .
Переход системы из одного состояния в другое удобно иллюстрировать
графом состояний ( рис. 22)
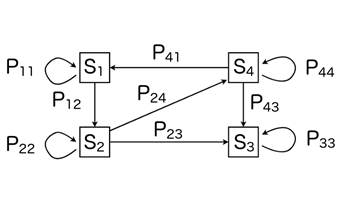
рис.22
Петля на рисунке означает, что в результате шага состояние системы не изменилось.
Нас интересует, в каком состоянии находится прибор в те или иные мо - менты времени tk (k= 0, 1, 2, ... ). Так как переходы из одного состояния в другое случайны, то правильнее задать вопрос, какова вероятность Pj (k),
что система на k- ом шаге находится в состоянии Sj .
Определение: Процесс, протекающий в такой системе называется марковс-
ким процессом с дискретными состояниями и дискретным
временем(марковской цепью), если для любого номера шага
k0 вероятность состояния системы в будущем (k> k0) зависит
от состояния системы в настояшем (k = k0) и не зависит от
от прошлого (k< k0).
Если процесс является марковской цепью, то для нахождения вероятно -
стей Pj(k) необходимо знать вероятности Pij(k) перехода системы из состоя-
нгия Si на k - 1 шаге в состояние Sj на k - ом шаге. Эти вероятности, как
правило, находят в результате анализа работы системы методами матема -
тической статистики в процессе эксплуатации системы.
Переходные вероятности Pij(k) формируют так называемую стохастичес-
кую матрицу
P11(k) P12(k) ... P1n(k)
P21(k) P22(k) ... P2n(k)
..................................
Pn1(k) Pn2(k) ... Pnn(k) .
Для нахождения вероятности Pj(k) необходимо еще знать состояние сис -
темы в начальный момент времени k = 0. Это состояние характеризуется
вероятностями Рi(0) того, что система в начальный момент находится в
определенном состоянии Si ( P1(0)+P2(0)+...+Pn(0) = 1 ).
Если известно, что в начальный момент система находится в определен -
ном состоянии Si , то Pi(0) = 1, Pj(0) = 0 (i ¹ j).
Зная состояние системы в начальный момент, по формуле полной вероят-
ности вычисляем вероятность нахождения системы в состоянии Sj после
первого шага
n
Pj(1) = P1(0) P1j(1) + P2(0) P2j(1) + ... + Pn(0) Pnj(1) = å Pi(0) Pij(1) .
i = 1
На втором шаге начальными условиями являются уже вероятности Pi(1),
найденные выше. Следовательно
n
Pj(2) = å Pi(1) Pij(2) и
i = 1
n
Pj(k) = å Pi(k-1) Pij(k) .
i = 1
Определение: Цепь Маркова называется однородной, если вероятности
Pij(k) одинаковы для всех шагов: Pij(k) = Pij .
Предположим, что процесс, протекающий в системе (рис. 22), является
однородной марковской цепью. Для этой системы стохастическая матрица
имеет вид
Р11 Р12 0 0
0 Р22 Р23 Р24
0 0 1 0
Р41 0 Р43 Р44 .
Пусть в начальный момент система находилась в состоянии S1 , т.е.
Р1(0) = 1, Р2(0) = Р3(0) = Р4(0) = 0, и Р11=0,8; Р12= 0,2 = Р22= Р23 ; Р24=Р41=0,6;
Р43= 0,1; Р44= 0,3.
Тогда Р1(1) = 0,8; Р2(1) = 0,2; Р3(1)= Р4(1)=0;
Р1(2) = Р1(1) Р11= 0,64;
Р2(2)= Р2(1)Р12+ Р2(1) Р22 = 0,2;
Р3(2)= Р2(1) Р23 = 0,04;
Р4(2)= Р2(1) Р24 = 0,12.
Следовательно Р1(3)= 0,584; Р2(3) = 0,168; Р3(3)= 0,092; Р4(3) = 0,156.
Марковская цепь является простейшей формой марковских процессов .
Более сложные варианты марковских процессов, имеющих большое прик -
ладное значение, рассмотрены в [ 1].
Вопросы для самопроверки
1. Дайте определение случайного процесса. Приведите примеры.
2. Дайте определение реализации случайного процесса. Что такое сечение случайного процесса(СП).
3. Дайте определение математического ожидания СП. Что характеризует математическое ожидание СП?
4. Дайте определение дисперсии СП. Что характеризует дисперсия СП?
5. Дайте определение ковариационной функции СП. Что характеризует дисперсия СП?
6. Какая функция называется автоковариационной функцией(АКФ) СП? Укажите ее основные свойства.
7. Какая функция называется взаимной ковариационной функцией(ВКФ) СП? Укажите ее основные свойства.
8. Дайте определение векторного СП. Какие функции характеризуют векторный СП?
9. Что понимается под вероятностными характеристиками СП.
10. Классификация СП по структуре реализации СП(т.е. по виду сечения Спи по времени).
11. Стационарные СП в узком и широком смысле.
12. Свойства АКФ стационарного в широком смысле СП.
13. Частотные характеристики СП: спектральная характеристика; спектральная плотность мощности.
14. Свойства спектральной плотности мощности СП.
15. Преобразования Винера – Хинчина.
16. Эргодические СП и их временные характеристики.
17. Гауссовский случайный процесс.
18. Марковский случайный процесс. Цепь Маркова. Переходные вероятности.
19. Дайте определение потока событий. Регулярный поток событий.
20. Свойства потоков событий. Простейший поток событий.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Общие указания
Контрольная работа выполняется студентом в отдельной тетради. Решение каждой задачи необходимо кратко пояснить и аккуратно записывать.
Студент должен быть готов дать во время экзамена(зачета) пояснения
по существу решения заданий.
Контрольная работа состоит из четырех заданий, в каждом из которых
в качестве k и m берутся две последние цифры студенческого билета, при -
чем k - предпоследняя цифра студенческого билета, m - последняя цифра
студенческого билета.
Задача 1. Задан случайный процесс Х(t) . Найти математическое
ожидание, ковариационную функцию и дисперсию случайного
процесса
У(t) = dХ(t)/dt
где u - случайная величина с известной плотностью распределе-
ния f(u).
| Предпоследняя цифра студенческого билета | Х(t) |
| 0 | 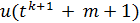
|
| 1 | 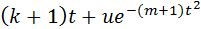
|
| 2 | 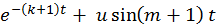
|
| 3 | 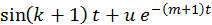
|
| 4 | 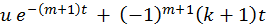
|
| 5 | 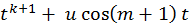
|
| 6 | 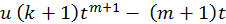
|
| 7 | 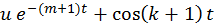
|
| 8 | 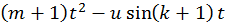
|
| 9 | 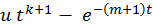
|
| Последняя цифра Студенческого билета | f(u) |
| 0 | c - u 2 ; u Î [ 0 ; 1 ] |
| 1 | c - (u -1) 2 u Î [ 1 ; 2 ] |
| 2 | u + 1 u Î [ 0 ; c ] |
| 3 | 1 - c × u 2 u Î [ -1 ; 1 ] |
| 4 | 1 + c × u ; u Î [ 0 ; 1 ] |
| 5 | c × u – 2 ; u Î [ 3 ; 4 ] |
| 6 | c /(u – 2) 2 ; u Î [ 0 ; 1,5 ] |
| 7 | c / u ; u Î [ 2 ; 3 ] |
| 8 | c / (u – 3) 2 ; u Î [ 0 ; 1 ] |
| 9 | c / u 2 ; u Î [ 2 ; 4 ] |
Выбор функций Х(t) и f(u) производится по двум последним цифрам
студенческого билета. При этом для функции Х(t) выбор значений k и m
производить следующим образом:
k - предпоследняя цифра студенческого билета;
m - последняя цифра студенческого билета.
Если k = 0 , то считать k = 3 ; если m = 0 , то считать m = 5.
Задача 2. Номер задачи выбирается по последней цифре студенческого билета 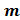 . Исходные данные в решаемой задаче выбираются по предпоследней цифре студенческого билета
. Исходные данные в решаемой задаче выбираются по предпоследней цифре студенческого билета 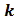 .
.
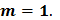 Корреляционная функция стационарного в широком смысле случайного процесса имеет вид:
Корреляционная функция стационарного в широком смысле случайного процесса имеет вид:
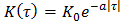
Найти дисперсию случайного процесса и его время корреляции 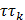 . Построит эскиз графика корреляционной функции и указать на нем значение времени корреляции.
. Построит эскиз графика корреляционной функции и указать на нем значение времени корреляции.
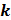
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
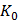
| 3 | 4 | 6 | 5 | 3 | 2 | 9 | 7 | 6 |
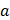
| 2 | 3 | 4 | 2 | 3 | 4 | 3 | 4 | 2 |
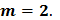 Спектральная плотность стационарного в широком смысле случайного процесса имеет вид:
Спектральная плотность стационарного в широком смысле случайного процесса имеет вид: 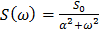 .Найти дисперсию случайного процесса и эффективную полосу частот
.Найти дисперсию случайного процесса и эффективную полосу частот 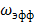 .
.
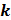
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
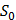
| 2 | 9 | 7 | 6 | 5 | 4 | 2 | 5 | 6 |
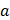
| 4 | 3 | 2 | 4 | 3 | 4 | 5 | 4 | 2 |
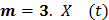 - стационарный в широком смысле случайный процесс с известными математическим ожиданием
- стационарный в широком смысле случайный процесс с известными математическим ожиданием 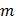 и корреляционной функцией
и корреляционной функцией 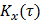 . Найти математическое ожидание, дисперсию и корреляционную функцию случайного процесса
. Найти математическое ожидание, дисперсию и корреляционную функцию случайного процесса 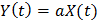 и доказать, что этот случайный процесс является стационарным в широком смысле.
и доказать, что этот случайный процесс является стационарным в широком смысле.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 3 | 5 | 6 | 7 | 4 | 5 | 4 | 3 | 2 |
 Корреляционная функция стационарного в широком смысле случайного процесса задана выражением:
Корреляционная функция стационарного в широком смысле случайного процесса задана выражением: 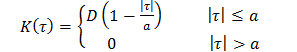 .Найти время корреляциии случайного процесса, нарисовать эскиз графика корреляционной функции и указать на нем значение времени корреляции.
.Найти время корреляциии случайного процесса, нарисовать эскиз графика корреляционной функции и указать на нем значение времени корреляции.
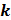
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
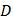
| 4 | 3 | 6 | 8 | 2 | 2 | 7 | 7 | 6 |
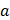
| 4 | 6 | 3 | 2 | 3 | 2 | 3 | 4 | 2 |
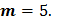 Корреляционная функция стационарного в широком смысле случайного процесса задана выражением:
Корреляционная функция стационарного в широком смысле случайного процесса задана выражением: 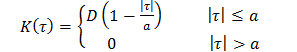 . Найти спектральную плотность данного случайного процесса.
. Найти спектральную плотность данного случайного процесса.
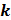
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
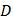
| 5 | 4 | 3 | 2 | 4 | 3 | 6 | 8 | 2 |
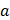
| 5 | 2 | 2 | 3 | 3 | 4 | 6 | 3 | 2 |
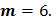 Спектральная плотность случайного процесса, стационарного в широком смысле, постоянна и равна
Спектральная плотность случайного процесса, стационарного в широком смысле, постоянна и равна 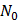 в полосе частот
в полосе частот 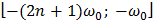 и
и 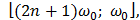 и нулю вне этих интервалов. Найти корреляционную функцию данного случайного процесса.
и нулю вне этих интервалов. Найти корреляционную функцию данного случайного процесса.
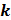
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 5 | 4 | 3 | 2 | 4 | 3 | 6 | 8 | 2 |
| 5 | 4 | 6 | 6 | 7 | 5 | 7 | 4 | 2 |
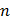
| 2 | 3 | 2 | 3 | 4 | 2 | 3 | 4 | 2 |
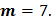 Спектральная плотность случайного процесса, стационарного в широком смысле, постоянна и равна
Спектральная плотность случайного процесса, стационарного в широком смысле, постоянна и равна 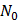 в полосе частот
в полосе частот 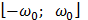 и нулю за пределами этого интервала. Найти корреляционную функцию данного случайного процесса.
и нулю за пределами этого интервала. Найти корреляционную функцию данного случайного процесса.
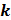
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
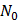
| 5 | 4 | 3 | 2 | 4 | 3 | 6 | 8 | 2 |
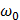
| 5 | 4 | 6 | 6 | 7 | 5 | 7 | 4 | 2 |
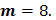 Случайный процесс X(t)- стационарный в широком смысле с известным математическим ожиданием
Случайный процесс X(t)- стационарный в широком смысле с известным математическим ожиданием 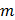 и корреляционной функцией
и корреляционной функцией 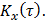 Найти математическое ожидание, дисперсию и корреляционную функцию случайного процесса
Найти математическое ожидание, дисперсию и корреляционную функцию случайного процесса 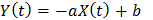 и доказать, что этот случайный процесс является стационарным в широком смысле.
и доказать, что этот случайный процесс является стационарным в широком смысле.
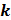
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
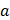
| 3 | 5 | 6 | 7 | 4 | 5 | 4 | 3 | 2 |
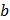
| 1 | 2 | 3 | 5 | 4 | 5 | 3 | 5 | 4 |
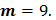 Дан случайный процесс
Дан случайный процесс 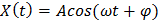 , где фаза
, где фаза 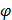 есть случайная величина, равномерно распределенная на отрезке
есть случайная величина, равномерно распределенная на отрезке 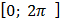 . Найти математическое ожидание, дисперсию и корреляционную функцию случайного процесса
. Найти математическое ожидание, дисперсию и корреляционную функцию случайного процесса 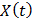 и доказать, что данный случайный процесс является стационарным в широком смысле.
и доказать, что данный случайный процесс является стационарным в широком смысле.
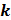
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
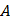
| 3 | 4 | 6 | 5 | 3 | 2 | 9 | 7 | 6 |
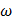
| 2 | 3 | 4 | 2 | 3 | 4 | 3 | 4 | 2 |
Задача 3. Цепь Маркова с тремя состояниями S1, S2, S3 характеризуется
однородной стохастической матрицей
Р11 0 Р13
Р21 Р22 0
Р31 Р32 Р33 ,
где Р11 = Р22 = Р33 = m/ m + 2 ; P13 = P21 = 2/ m + 2 ; P31= P32= 1/ m+2;
m - последняя цифра студенческого билета; если m = 0, то взять m=2.
Требуется: 1) изобразить граф состояний системы (сделать чертеж);
2) найти вероятность Рj(3) состояния системы на третьем шаге, если в
начальный момент система находилась в состоянии:
S1 для вариантов, у которых m = 0, 3, 6 и 9;
S2 для вариантов, у которых m = 1, 4 и 7;
S3 для вариантов, у которых m = 2, 5 и 8.








