Cпектральное разложение стационарных случайных процессов
При изучении детерминированных процессов( или сигналов) и реакции на них линейных систем с постоянными параметрами широко используются спектральные представления, базирующиеся на возможности представления сигналов рядом или интегралом Фурье (гармонический анализ). При этом математически сравнительно просто и физически наглядно можно найти сигнал на выходе линейной системы простым пересчетом отдельных спектральных составляющих входного сигнала через комплексную передаточную характеристику с последующим принципом суперпозиции. Представляется естественным желание распространить гармонический анализ на случайные процессы для решения аналогичных задач, хотя физический смысл результатов будет при этом несколько другим. Наиболее просто эта задача решается для стационарных с.п. с использованием понятия спектральной плотности процесса.
Стационарный в широком смысле случайный процесс X(t), заданный каноническим разложением вида
n n
X(t) = mx + å (uk× cos wkt + vk× sin wkt ) = mx + å zk(t) , (37)
k = 0 k = 0
где uk и vk - центрированные случайные величины, для которых выполняются условия M[vi× vj] = M[ui× uj] = Di , если i = j и M[vi× vj] = M[ui× uj] = 0 при i ¹ j;
M[vi ×uj ] = 0 для всех i, j = 0,1, ... , n; называется случайным процессом с
дискретным спектром.
Автокорреляционная функция такого процесса будет
n n n
Kx(t1,t2) = M[ å zk(t1) ×å zk(t2)] = å M[ zk(t1) zk(t2)] =
n k = 0 k = 0 k = 0
= å M[ uk2 cos wkt1 cos wkt2 + ukvk cos wkt1 sin wkt2 +
k = 0
+ ukvk sin wkt1 cos wkt2 + vk2 sin wkt1 sin wkt2 ] =
n
= å Dk(cos wkt1 cos wkt2 + sin wkt1 sin wkt2 ) =
k = 0
n n
= å Dk cos wk (t1 - t2) = å Dk cos wkt = Kx(t) . (38)
k = 0 k = 0
Отсюда следует, что дисперсия процесса определяется суммой дисперсий всех
гармоник n
Dx = Kx(0) = å Dk .
k = 0
Представления (37) и (38) называются спектральными представлениями соответственно случайного процесса и его корреляционной функции.
Стационарный случайный процесс X(t) называется случайным процессом с
непрерывным спектром, если существует такая действительная неотрицательная функция Sx(w), определенная на всей числовой оси частот -¥< w < + ¥ , называемая спектральной плотностью ( или спектральной плотностью мощности) и задаваемая преобразованием Фурье от
ковариационной(автоковариационной) функции
Sx(w) = 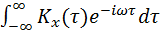 . (39)
. (39)
При этом имеет место обратное преобразование Фурье вида
Kx(t) = 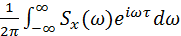 . (40)
. (40)
Пара преобразований Фурье (39) и (40) называется преобразованием Винера - Хинчина .
Спектральная плотность Sx(w) обладает свойствами:
1) спектральная плотность мощности неотрицательная функция
Sx(w) ³ 0, при -¥< w < + ¥ ;
2) спектральная плотность мощности четная функция
Sx(w) = Sx(-w) ;
это вытекает из четности ковариационной функции стационарного в широком
смысле случайного процесса Kx (t) = Kx (-t) .
3) Dx = Kx(0) = 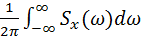
- интеграл от спектральной плотности в пределах wÎ(0;+¥) равен дисперсии
стационарного случайного процесса.
Для стационарного в широком смысле случайного процесса в силу четности
ковариационной функции формулы (39) и (40) будут иметь вид
Sx(w) = 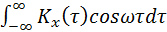 =
= 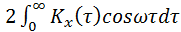 . (41)
. (41)
Kx(t) = 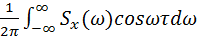 =
= 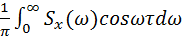 . (42)
. (42)
Для стационарного в широком смысле с.п. имеют место следующие важные
понятия :
- эффективная “ширина” спектральной плотности мощности, определяемая соотношением
¥
Dw = (1/Sx(0)) × ò Sx(w) dw ; (43)
-¥
- интервал корреляции (или эффективная длительность ковариационной функции) Dtк, определяемый соотношением
¥
Dtк = (1/Kx(0)) × ò Kx(t) dt . (44)
-¥
Cмысл определений (43) и (44) состоит в том, что площади под кривыми S x(w) и Kx(t) приравниваются к площадям прямоугольников с основаниями Dw и Dtк и высотами S x (0) и Kx(0) cоответственно (см. рис. 16 и рис. 17).
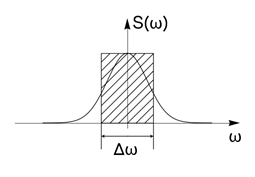
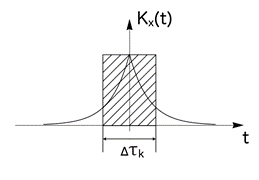
рис. 16 рис. 17
Пример 10. Автоковариационная функция стационарного с.п. X(t) задана в
виде Kx(t) = sx2 e-a½t½ ; -¥ <t< +¥ ; a > 0 .
Найти спектральную плотность мощности S x(w) и эффективные
характеристики Dw и Dtк .
Решение: Данная ковариационная функция является четной функцией, тогда
по определению (41) имеем
Sx(w) = 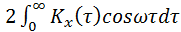 =
= 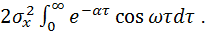
Применяя для вычисления полученного интеграла метод интегрирования по частям, найдем
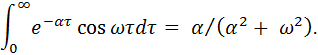
Окончательно спектральная плотность мощности с.п. будет равна
S x(w) = 2sx2×a / p(w2 + a2) . (45)
Для определения эффективной ширины спектра Dw предварительно
найдем
S x(0) = 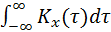 = 2×sx2 / a p.
= 2×sx2 / a p.
Окончательно получим
Dw 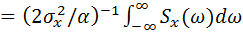 =
= 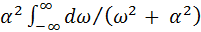 = a p.
= a p.
Для вычисления интервала корреляции Dt предварительно найдем
Kx(0) =Dx= 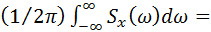
= 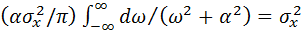
Подставляя полученный результат в формулу (44) окончательно
получим
Dtк = 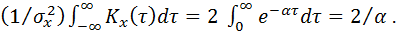 ð
ð
Между эффективной шириной спектра Dw и интервалом корреляции Dt имеет место количественная связь, которая выражается в виде соотношения неопределенности
Dw× Dtк ³ 2p .
Это соотношение показывает, что чем “уже” ширина спектра Dw, тем больше интервал корреляции Dtк и наоборот.
Важное значение в электро - и радиотехнике имеет понятие “белого шума”
Под “белым” шумом понимается стационарный с.п. n(t) в широком смысле с
дельта-видной корреляционной функцией, т.е. ковариационная функция такого с.п. равна произведению дельта-функции d(t) на постоянную величину N0/2
Kx(t) = d(t) × N0/2 .
Спектральная плотность мощности такого процесса будет
Sx(w) = 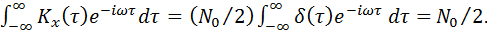
Поскольку в природе существуют только положительные частоты, то спект -
ральная плотность мощности S+(w) на положительных частотах будет
S+(w) = 2 S(w) = N0 .
Здесь величину N0 называют интенсивностью процесса n(t) , а сам процесс n(t),
обладающий равномерной (постоянной) спектральной плотностью на всех частотах wÎ(-¥,+¥), также называют “белым шумом”. Белый шум физически неосуществим, т.к. его дисперсия Dn (t) бесконечна.
Белый шум является полезной математической идеализацией, применимой в тех случаях, когда интервал корреляции много меньше существующих постоянных времени системы, на которую он воздействует , или, иначе, когда в пределах амплитудно-частотной характеристики системы спектральную плотность воздействующего реального шума можно приближенно считать постоянной.
Пример 11. Спектральная плотность Sx(w) стационарного в широком смысле
случайного процесса X(t) имеет вид ( рис. 18)
N0/2 при wÎ(-w2; -w1) и при wÎ(w1; w2) ;
Sx(w) = í
0 , в остальных случаях.
Найти ковариационную функцию с.п. X(t).
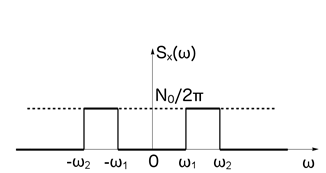
рис.18
Решение. По определению ковариационной функции (47) получим
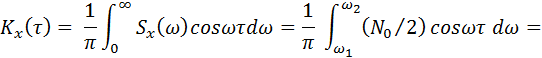
= (N0/2pt)×( sin w 2 t - sin w 1 t) = (N0/2pt)×2×cos[( w 2 + w 1)×t/2]×sin[(w 2-w 1)×t/2] =
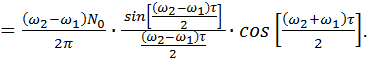 (46)
(46)
При w1 = 0 область определения спектральной плотности станет ½w½< w2 , а
ковариационная функция будет
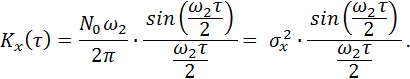 (47)
(47)
Графики ковариационных функций, соответствующие формулам (46) и (47)
приведены на рисунках 19 и 20.
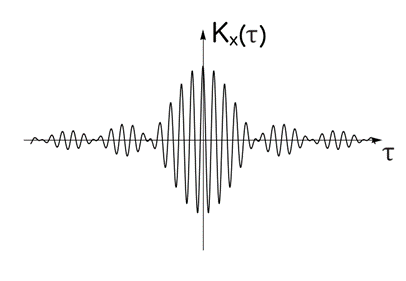
Рис.19
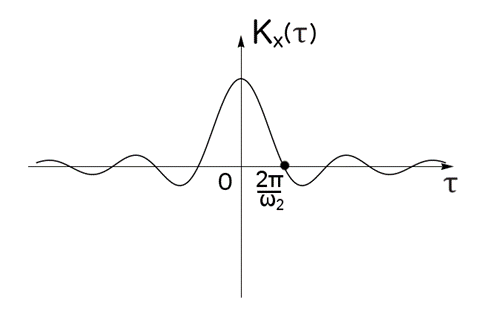
рис.20








