Cтационарные случайные процессы
Случайный процесс X(t) , -¥< t < +¥ , называется стационарным в узком
смысле ( или строго стационарным ) , если распределение вероятностей любых случайных величин X(t1), X(t2), ... , X(tn) такое же как и случайных величин X(t1+t), X(t2 + t), ... , X(tn + t), имеющих сдвиг по времени на постоянную величину t , -¥< t< +¥ . Если, например, X(t) случайная функция непрерывного типа, то условие стогой стационарности имеет вид
f (x1, ... , xn; t1, ... ,tn) = f (x1 , ... , xn; t1 + t, ... ,tn + t ) . (29)
Случайный процесс X(t), для которого M [X(t)]2 < +¥ , называется стационарным в широком смысле, если его среднее значение и дисперсия не зависят от времени, а ковариационная функция Kx(t1,t2) зависит лишь от разности t2 - t1 :
M[X(t)] = m = const ;
D [X(t)] = s2 = const ; (30)
Kx (t1,t2) = Kx(t) ; t = t2 - t1 .
Для нормальных случайных процессов оба понятия стационарности совпадают.
Автоковариационная функция стационарного в широком смысле процесса
обладает следующими свойствами:
1) Kx(t) = Kx(-t) ;
2) ½ Kx(t) ½ £ Kx(0) = D[X(t)]; (31)
3) Функция Kx(t) неотрицательно определена.
Если стационарная в широком смысле случайная функция X(t) является дифференцируемой и y(t) = dX(t) / dt , то y(t) - также стационарная в широком смысле случайная функция, для которой
M[y(t)] = 0; Ky(t) = - d2Kx(t) / dt2 ; D[y(t)] = Ky(0). (32)
Эргодические случайные процессы
Случайный процесс будем называть эргодическим , если любая его вероятностная характеристика, полученная усреднением по множеству реализаций, с вероятностью, сколь угодно близкой к единице, равна временно′му среднему, полученному усреднением за достаточно большой промежуток времени одной единственной реализации случайного процесса. Из эквивалентности двух способов усреднений по множеству и по времени следует, что для эргодического с.п. нет необходимости изучать большую совокупность реализаций , которой исследователь, как правило, не располагает, а достаточно одной реализации, наблюдаемой в течение длительного промежутка времени. Другими словами, эргодическое свойство состоит в том, что любая реализация стационарного с.п. является полным представителем всей совокупности реализаций стационарного с.п.
В большинстве случаев на практике интересуются не всеми, а только отдельными характеристиками процесса ( математическим ожиданием, ковариационной функцией и одномерной функцией распределения или плотностью вероятностей).
В связи с этим можно ввести понятие временны′х характеристик реализаций с.п.
Пусть реализация X(k)(t) случайного процесса наблюдается в течение промежутка времени 2Т; -Т < t < Т .
Временны′м средним или средним по времени от реализации стационарного с.п. называется числовая характеристика, определяемая выражением
1 T
<X(k)(t)> = lim ¾ ò X(k)(t) dt , (33)
T®¥ 2T -T
которую можно трактовать как постоянную составляющую этой реализации.
Средним по времени квадратом от реализации стационарного с.п. называется числовая характеристика, определяемая выражением
1 Т
<[X(k) (t)]2> = lim ¾ ò [X(k)(t)]2 dt . (34)
T®¥ 2T -T
Если реализация X(k)(t) представляет изменение напряжения или тока на единичной нагрузке, то средний во времени квадрат равен средней мощности данной реализации.
Временно′й ковариационной (автоковариационной) функцией реализации X(k)(t) , будем называть действительную величину, определяемую выражением
1 T
< X(k)(t) X(k)(t+t) > = lim ¾ ò [X(k)(t)-mx][ X(k)(t+t)-mx] dt . (35)
T®¥ 2T -T
Временно′й взаимной ковариационной функцией реализаций X(k)(t) и У(k)(t)
будем называть величину, определяемую выражением
1 T
< X(k)(t) У(k)(t+t) > = lim ¾ ò [X(k)(t)-mx][ У(k)(t+t)-mу] dt . (36)
T®¥ 2T -T
Пример 7. Пусть случайный процесс X(t) задан как неслучайная величина
X(t) = b. Найти его характеристики; определить, является ли этот
процесс стационарным и обладает ли он свойством эргодичности?
Решение. Найдем M[X(t)] = a; Dx(t) = Kx(t,t) = 0. Следовательно (30)
случайный процесс X(t) является стационарным и, кроме этого, он
будет и эргодическим. ð
Пример 8. Случайный процесс задан в виде X(t) = u, где u - случайная
величина.
Найти его характеристики. Определить является ли этот процесс
стационарным и обладает ли он свойством эргодичности ?
Решение. Найдем M[X(t)] = mu ; Kx(t1,t2) = M[(u-mu)2] = D(u) =Du .
Следовательно случайный процесс X(t) - стационарен, и, так как
lim Kx(t) = Du ¹ 0 , то он не обладает эргодическим свойством. ð
τ®¥
Пример 9. Случайный процесс X(t) представляет случайную телеграфную
волну которая образуется следующим образом. На оси 0t имеется
простейший (пуассоновский) поток событий с интенсивностью l.
Случайный процесс X(t) попеременно с равной вероятностью
принимает два значения -1 и +1. Одна из возможных реализаций
такого с.п. приведена на рис. 15. Найти характеристики с.п. X(t) .
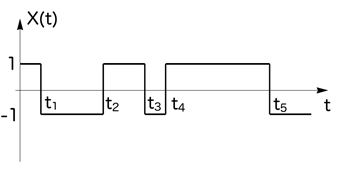
рис. 15
Решение. Закон распределения с.п. X(t) имеет вид
ê -1 ê +1 ê
X(t) : ¾¾¾¾¾¾
ê 1/2 ê 1/2 ê .
Найдем M[X(t)] = (-1)× 1/2 + (+ 1)× 1/2 = 0
D[X(t)] = (-1)2× 1/2 + (+ 1)2× 1/2 = 1.
Зафиксируем произвольные моменты времени t1 и t2 и будем искать ковариационную функцию в виде
Kx(t1,t2) = M[(X(t1) - mx) (X(t2) - mx)] = M[X(t1) X(t2)] .
Здесь произведение X(t1) X(t2) может принимать только два значения:
+1, если за интервал времени (t1, t2) произошло четное число перемен знака у телеграфной волны, и -1 , если за интервал (t1, t2) число перемен знака было нечетным. Найдем вероятность того, что на интервале t = t2 - t1 (t > 0) произошло четное число перемен знака
P(n = 2k) = P[ X(t1)X(t2) = +1] = 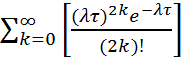 =
=
= 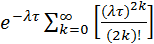 = e -lt × ch lt = (1 + e -2lt) / 2.
= e -lt × ch lt = (1 + e -2lt) / 2.
Отсюда вероятность того, что за интервал времени t = t2 - t1 произойдет нечетное число перемен знака будет равна
P(n¹2k) = 1 - P(n=2k) = (1 - e-lt)/ 2.
Тогда Kx(t1,t2) = M[X(t1) X(t2)] = (-1)× P(n¹2k) + (+1)× P(n=2k) = e-2lt .(à)
Для случая, когда t = t1-t2 < 0 (т.е. t2-t1=-t) , получим
Kx(t1,t2) = e-2l(-)t = e 2lt . (àà)
Объединяя две последние формулы (à) и (àà) в одну получим окончательно
Kx(t1,t2) = Kx(t) = e -2l½t½.
Полученные результаты позволяют сделать вывод о том, что случайный процесс – «телеграфная волна» - является стационарным и обладает
свойством эргодичности относительно математического ожидания, т.к.
lim Kx(t) = 0.
t®¥








