Определение: Нормированной корреляционной (автокорреляционной)

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

функцией случайного процесса называется нормированная

ковариационная (автоковариационная ) функция, получаемая

делением ковариационной функции на произведение

среднеквадратичных отклонений

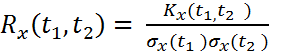. ( 11 )

Нормированная корреляционная функция случайного процесса R_x (t₁,t₂) обладает свойствами:

1) при t₁ = t₂ = t нормированная корреляционная функция равна 1

K_x(t,t) D_x( t)

R_x(t,t) = ¾¾¾¾¾ = ¾¾¾¾ = 1.

s_x(t) s_х(t) s_x² (t)

2) нормированная корреляционная функция случайного процесса симметрична относительно своих аргументов

R_x(t₁,t₂) = R_x(t₂,t₁).

3) нормированная корреляционная функция случайного процесса принимает значения от -1 до +1, т.е. ½R_x(t₁,t₂) ½ £ 1.

!Замечание! : В некоторых учебниках и задачниках, например [4],[5], корреляционная функция (10) называется ковариационной функцией, а нормированная корреляционная функция называется корреляционной функцией.

Более сложным объектом по сравнению со случайным процессом Х(t) является векторный случайный процесс Х^* (t), состоящий из k - компонент - случайных процессов Х _i (t)

Х^* (t) = {Х₁ (t), Х₂ (t), ... , Х _k (t) } . ( 12 )

Каждая компонента векторного случайного процесса (12) имеет характеристики:

М [Х_i (t)] = m _i (t) ; D[X_i (t)] = ϭ_i ² ; K(x_i ; t₁, t₂) = K_i (t₁ , t₂).

Для определения зависимости между компонентами векторного с.п. используют взаимную корреляционную функцию K_{i j} (t₁, t₂) двух случайных процессов.

Определение: Взаимной корреляционной функцией K_{i j} (t₁, t₂) двух случай-

ных процессов Х_i (t) и Х_j (t) называется неслучайная функция

двух аргументов t₁ и t₂ , которая при каждой паре значений

( t₁, t₂) равна ковариации двух сечений случайных процессов

Х_i (t) и Х_j (t) и вычисляется по формуле

K_{i j} (t₁, t₂) = М [Х⁰_i (t₁) Х⁰_j (t₂)] = M[(Х_i (t₁) - m_x(t₁)) (Х_j (t₂) - m_x(t₂))] =

= M[Х_i (t₁) Х_j (t₂) ] - m_i (t₁)m_j(t₂) . (13)

рис. 4 рис.5

Свойства взаимной корреляционной функции:

1) взаимная корреляционная функция K_{i j} (t₁, t₂) в общем случае не равна

K_{i j} (t₂, t₁), т.к. ковариация между сечениями Х_i (t₁) и Х_j (t₂) в общем случае не равна ковариации сечений Х_i (t₂) и Х_j (t₁)

К_{i j} (t₁, t₂) ¹ К_{i j} (t₂, t₁) ;

2) при одновременной перемене мест индексов и аргументов взаимная корреляционная функция не меняется

К_{i j} (t₁, t₂) = К_{j i} (t₂, t₁).

3) при равенстве индексов i = j взаимная корреляционная функция равна автокорреляционной функции

К_{i j} (t₁, t₂) = М[ Х_i (t₁) Х_j (t₂)] = К_i (t₁, t₂) .

Нормированная взаимная корреляционная функция определяется по формуле

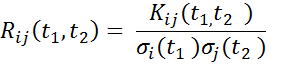. ( 14 )

Из свойств 1) ¸ 3) следуют свойства нормированной взаимной корреляционной функции:

а. R_{i j} (t₁, t₂) = R_{j i} (t₂, t₁) ;

б. R_{i i} (t₁, t₂) = R_i (t₁, t₂) .

Таким образом в качестве характеристик векторного случайного процесса

Х^* (t) = {Х₁ (t), Х₂ (t), ... , Х_n (t) }

рассматривают:

1. математическое ожидание векторного с.п. Х^* (t) - неслучайный вектор, зависящий от параметра t :

m_x(t) = { m₁(t), m₂(t), ... , m_k(t) },

где m_i(t) = M[ X_i (t) ] - математическое ожидание i - ой компоненты векторного с.п.

2. квадратную матрицу взаимных корреляционных функций

(размерности k´k) векторного с.п. :

K₁₁(t₁, t₂) K₁₂(t₁, t₂) ... K_1k(t₁, t₂)

K₂₁(t₁, t₂) K₂₂(t₁, t₂) ... K_2k(t₁, t₂)

½½ K_{i j} (t₁, t₂) ½½ = . . ( 15 )

. .

K_k1(t₁, t₂) K_k2(t₁, t₂) ... K_kk(t₁, t₂) ,

где каждая компонента K_{i j} (t₁, t₂) определяется по формуле ( 13 ).

Случайные процессы X_i ( t ) и X_j ( t ) называются некоррелированными, если соответствующая им взаимная корреляционная функция K_{i j} (t₁, t₂) обращается в ноль при любых значениях аргументов t₁ t₂ для всех i ¹ j.

Векторный случайный процесс X^* ( t ) называется процессом с некоррелированными составляющими, если матрица взаимных корреляционных функций является диагональной, т.е. К_{i j} ( t₁, t₂) при всех

i ¹ j.

В простых задачах случайные процессы можно представлять через элементарные случайные функции.

Определение: Элементарная случайная функция - это такая функция

аргумента t, в которой зависимость от t представлена

неслучайной элементарной функцией, а параметром является

одна или несколько случайных величин, не зависящих от

аргумента t.

Примеры элементарных случайных функций:

1) Y (t) = X ×e ^{- t} (t> 0) ,

где Х - непрерывная случайная величина с известным законом распределения

(например, равномерным на интервале [ -1, +1] ) ; e ^{- t} - элементарная функция;

2) Y (t) = e ^{- X× t} (t>0) ,

где Х - случайная величина , принимающая только положительные значения;

3) Y (t) = a×t + X;

4) Y (t) = a + X× t ;

5) Y (t) = X× cos (a× t) ;

где Х - случайная величина; a - неслучайный параметр.

Семейства реализаций случайных процессов 1) ¸ 5) представлены на рисунках 6 ¸ 10 :

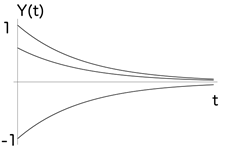
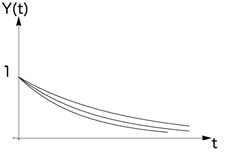
рис. 6 рис. 7

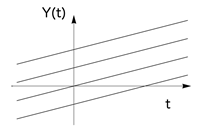
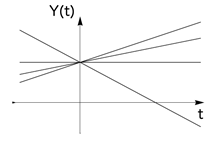
рис. 8 рис. 9

рис. 10

Рассмотрим некоторые примеры на определение основных характеристик случайных процессов, представленных элементарными функциями.

Пример 1. Элементарная случайная функция имеет вид Y (t) = X e ^{- t} (t>0),

где Х - равномерно распределенная на отрезке [ a, b ] случайная

величина . Найти характеристики с.п. Y (t) :

1) математическое ожидание М_у (t) ;

2) дисперсию D_y (t) ;

3) корреляционную К_у (t₁, t₂) и нормированную корреляционную

R _y (t_1, t₂) функции.

Решение: 1) Используя свойства математического ожидания получим

М_у(t) = М ( Х e^{- t}) = e ^{- t} M (X), где М(Х) = (a+b)/ 2 ; Þ M_y(t) = (a+b)× e^{- t} .

2) D _y (t) = D (X×e ^{- t}) = (e^{- t})× D(x) = (b-a)²× e^{- 2 t} / 12, где D(x) = (b - a)² /12 .

3) K _y (t₁, t₂) = M [(Y(t₁) - M_y(t₁))×( Y(t₂) - M_y(t₂))] = e ^{- (t}₁^{+ t}₂⁾ M[ (X - M(X))²] =

= e^{- (t}₁^{+ t}₂⁾ ×D(X).

При t₁ = t₂ = t в данном случае получим К_у(t, t ) = e ^{- 2t} D(x) = D_y (t)

Корреляционная функция для с.п. У (t) будет

R_y (t₁, t₂) = 1.

Пример 2. Элементарная случайная функция имеет вид У (t) = e ^{- хt} (t>0),

где случайная величина Х распределена по показательному

закону с плотностью f (x) = l× e ^{- l x} (x>0 ; l>0). Найти

характеристики с.п. У (t) :

1) М_у(t) ; 2) D_y(t) ; 3) K_y(t₁, t₂) и R_y(t₁, t₂) .

Решение: 1) По определению математического ожидания случайной величины найдем +¥ _+¥

М_у (t) = М (e ^{- хt}) = ò l× e ^{- xt} e ^-l dx = -l×(t + l)^-1 e^{- (t + l) x} ½ = l/( t+ l).

° ⁰

2) По определению дисперсии имеем D_y( t) = M[ Y²(t) ] - M² [ Y(t) ], где

_{+¥ +¥}

M[ Y²(t) ] = ò l e ^{- 2xt} e ^{- x} dx = [-l/( 2t+l)] e ^{- ( l + 2t) x} ½ = l/( 2t + l).

^{0 0}

Тогда D_y(t) = l/( t+ l) - [l/( 2t + l)]² = lt²/(2t + l) (t + l) .

3) Предварительно найдем M[ Y(t₁) Y(t₂)] = M( e^{- хt}₁ e^{- хt}₂) =

_+¥ l

= ò e ^{- x(t + t )} l e ^{- x} dx = ¾¾¾¾ ;

⁰ l + t₁ + t₂

Тогда K_y ( t₁, t₂) = M[ Y(t₁) Y(t₂)] - M_y(t₁) M_y(t₂) =

l l² l t₁ t₂

= ¾¾¾¾ - ¾¾¾¾¾¾ = ¾¾¾¾¾¾¾¾¾¾¾ .

l + t₁ + t₂ (t₁ + l) (t₂ + l) (l + t₁ + t₂) (t₁ + l) (t₂ + l)

l t²

При t₁ = t₂ = t получаем K_y (t, t) = D_y (t) = ¾¾¾¾¾¾ .

(l+ t)² (l + 2t)

Далее по определению найдем

_{_________ _________}

K_y( t₁, t₂) Ö 2t₁ + l × Ö 2t₂ + l

R_y (t₁, t₂) = ¾¾¾¾ = ¾¾¾¾¾¾¾¾¾ .

s_y(t₁) s_y(t₂) l + t₁ + t₂

Пример 3. Элементарная случайная функция имеет вид

Z ( t ) = Х× cos wt + У× sin wt , где w - постоянная величина; Х и У

- взаимно независимые гауссовские случайные величины с

нулевыми математическими ожиданиями m_x( t ) и m_y( t ) = 0 и

дисперсиями D (x) = D (y) = s² .

Найти одномерную f (z, t) и двумерную f ( z₁, z₂; t₁, t₂ ) плотности

распределения вероятностей.

Решение: Функции cos wt и sin wt являются детерминированными функциями,

т.е. известными функциями в любой момент времени при любом

значении параметра w . Тогда случайная величина Z = Z ( t ) при

любом фиксированном значении t представляет собой линейную

комбинацию гауссовских случайных величин и, в силу этого, также является гауссовской случайной величиной.

По этому для определения плотностей распределения f (z, t) и f ( z₁, z₂; t₁, t₂ )

необходимо найти математическое ожидание М_z ( t ) и корреляционную функ-

цию K_z ( t₁, t₂) . Так как m_x ( t ) и m_y ( t ) = 0 , то математическое ожидание

M_z ( t ) будет

M_z ( t ) = M [x× cos wt + y× sin wt] = cos wt× M(x) + sin wt×M(y) = 0.

Далее

K_z( t₁, t₂ ) = M[ z( t₁ ) z( t₂ ) ] = M[(x× cos wt₁ + y× sin wt₁)( x× cos wt₂ + y× sin wt₂)]=

= cos wt₁ cos wt₂ M(x²) + sin wt₁ cos wt₂ M(xy) + cos wt₁ sin wt₂ M(xy) +

+ sin wt₁ sin wt₁ M(y²) = cos wt₁ cos wt₂ M(x²) + sin wt₁ sin wt₁ M(y²) =

= cos wt₁ cos wt₂ s² + sin wt₁ sin wt₁ s² = s² cos w(t₂ - t₁),

поскольку M(xy) = M(x)× M(y) = 0.

Дисперсию D_z (t) получим из формулы для К_z (t₁ ,t₂), положив

t₁ = t₂ = t

D_z (t) = K_z (t, t) = s² .

Тогда одномерная функция плотности будет иметь вид

1

f (z, t) = ¾¾¾ exp { - [ z (t) ]² / 2s² }.

Ö 2 p s

Для нахождения двумерной функции плотности вероятностей вспомним функцию плотности двумерной гауссовской случайной величины

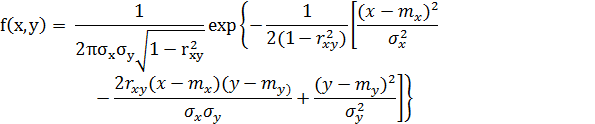
В нашем случае s_x = s_{y =} s ; r_xy = K_xy / s_xs_y = s² cos w(t₂-t₁) / s² = cos wt ,

где ( t₂ - t₁) = t . Тогда искомая двумерная плотность вероятностей будет

.

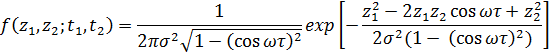Классификация случайных процессов.

Рассмотрим два варианта классификации случайных процессов.

1. Классификация случайных процессов по характеру реализаций x_i (t) с.п.,

т.е. в зависимости от возможных значений, принимаемых случайной функцией

X(t) и ее аргументом t.

Случайный процесс Х( t ) называется процессом с дискретным временем, если система в которой он протекает, может менять свои состояния только в моменты времени t₁, t₂, ... , t_i, ... , число которых конечно или счетно. Здесь множество параметров Т - дискретное множество.

Случайный процесс X(t) называется процессом с непрерывным временем, если переходы системы из состояния в состояние могут происходить в любой момент времени t наблюдаемого промежутка tÎ Т .

Случайный процесс X(t) называется процессом с непрерывными (дискретными) состояниями, если его сечение в любой момент времени t представляет непрерывную (дискретную) случайную величину.

Исходя из выше изложенного различают следующие виды случайных процессов:

1) Дискретная случайная последовательность - случайный процесс с дискретным временем и дискретным множеством состояний ( рис. 11). Процессы такого вида получаются после аналого-цифрового квантования по амплитуде и по времени.

2) Случайная последовательность - случайный процесс с дискретным временем и непрерывными состояниями (рис. 12 ).

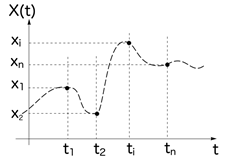
рис. 11 рис. 12

3) Дискретный (разрывный ) случайный процесс - с.п. с непрерывным временем и дискретными состояниями ( рис. 13).

4) Непрерывный( непрерывнозначный) случайный процесс - с.п. непрерывным временем и непрерывными состояниями (рис. 14). Примерами такого с.п. могут служить: напряжение в сети электропитания; амплитуда звукового сигнала на выходе радиоприемника и т.д.

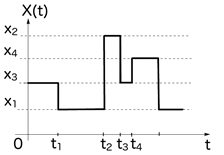
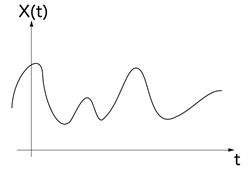
рис. 13 рис. 14

2. Классификация случайных процессов по виду закона распределения отдельного сечения или совокупности сечений процесса.

2-1. Гауссовский случайный процесс.

Случайный процесс называется гауссовским, если все его конечномерные расп ределения являются гауссовскими (нормальными). Многомерная плотность распределения вероятностей задается формулой

,

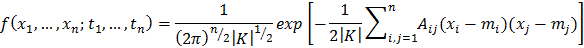(16)

где ½К½ - определитель ковариационной матрицы ( 15 ), А_{i j} – алгебраическое

дополнение элемента К_{i j} матрицы ( 15 ).

Векторная форма записи формулы ( 16 ) имеет вид

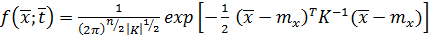(17)

где символ ( ) ^Т означает операцию транспонирования.

Гауссовский случайный процесс обладает следующими важными свойствами:

а) гауссовский с.п. исчерпывающим образом определяется заданием математического ожидания m_x(t) и ковариационной функцией K_ij (t₁,t₂), что видно из формулы( 16 );

б) для гауссовского с.п. некоррелированность значений процесса тождественна их независимости . Тогда многомерная плотность распре -

деления ( 16 ) распадается в произведение одномерных гауссовских плотностей

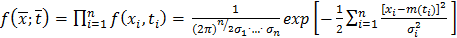(18)

2 – 2. Винеровский процесс или процесс броуновского движения

Винеровский процесс служит приближенной моделью хаотического (случайного) движения частиц.

Винеровским процессом, выходящим из начала координат, называется такой с.п. Х(t) , который обладает следующими свойствами:

а) Х(t = 0) = 0 ;

б) для любых 0 £ t₁ <t₂ < , ... ,< t_n случайные величины Х(t₂) -Х(t₁); Х(t₃) -Х(t₂); ... ; Х(t_n) -Х(t_n-1) независимы ;

в) случайные величины Х(t) - Х(s) распределены по нормальному закону с параметрами М [ Х(t) - Х(s) ] = 0 ; D [ Х(t) - Х(s) ] = t - s ; 0 £ s £ t .

2 – 3. Пуассоновский случайный процесс

Пуассоновским называется такой случайный процесс Х(t) с параметром l(l>0), который удовлетворяет следующим условиям:

а) Х(t = 0) = 0 ;

б) для любых 0 £ t₁ <t₂ < , ... ,< t_n случайные величины Х(t₂) -Х(t₁); Х(t₃) -Х(t₂); ... ; Х(t_n) -Х(t _n-1) независимы ;

в) случайные величины Х(t) - Х(s) ; 0 £ s £ t, распределены по закону Пуассона с параметром l ( t - s)

Р[ Х(t) - Х(s) = k ] = [l ( t - s)]^k × e ^{- l (t - s )} / k ! , k = 0,1,2, ... .

2 – 4. Марковский случайный процесс.

Марковским случайным процессом ( процессом А.А. Маркова) называется с.п. без последействия , для которого исчерпывающей вероятностной характеристикой является условная функция распределения, удовлетворяющая для любых n моментов времени t₁ < t₂ < , ... , < t_n соотношению

F ( x_n , t_n / x₁, t₁; ... ; x_n-1, t_n-1 ) = F ( x_n, t_n / x_n-1 , t_n-1 ). ( 19 )

Если существует условная плотность вероятностей f ( x_n, t_n / x_n-1 , t_n-1 ), которая называется переходной плотностью вероятностей , то важное свойство марковского с.п. состоит в том, что его совместная плотность вероятностей может быть представлена в виде произведения переходных вероятностей

_n

f(x₁, ... , x_n;t₁, ... ,t_n) = f (x₁, t₁)× P f (x_i , t_i / x_i-1 , t_i-1 ) . ( 20 )

^{i = 2}

Таким образом для марковского процесса условные функции распределения и переходные плотности вероятностей f (x_i , t_i / x_i-1 , t_i-1) его значений x_i в момент времени t_i зависят только от значений x_i-1 в момент t_i-1 и не зависят от значений процесса до момента времени t_{i - 1} .

Примерами марковских процессов являются пуассновский и винеровский с.п.

Для марковских процессов также применима классификация по “времени” и

по “состояниям”.

2 – 5. Случайные процессы с независимыми приращениями.

Случайным процессом с независимыми приращениями называется такой с.п.

Х(t) , приращения которого на непересекающихся отрезках времени не зависят

друг от друга и для t₁ <t₂ < , ... ,< t_n случайные величины

Х(t₂) -Х(t₁); Х(t₃) -Х(t₂); ... , Х(t_n) -Х(t_n-1) независимы .

Примерами таких с.п. являются рассмотренные выше винеровский и пуассо -

новский процессы.

Здесь же можно отметить случайные процессы с некоррелированными приращениями, для которых приращения на неперекрывающихся отрезках времени некоррелированы.

2 – 6. Стационарные случайные процессы.

Стационарным случайным процессом “в узком” смысле называется процесс

Х(t) , для которого для любого действительного t его конечномерные распределения не меняются при сдвиге на величину t

F(x₁, ... , x_n; t₁, ... ,t_n) = F (x₁ , ... , x_n; t₁ + t, ... ,t_n + t ) ,

где t₁ + t, ... ,t_n + t Î Т.

Стационарным случайным процессом “в широком” смысле называется про- цесс Х(t) , для которого существуют первый и второй начальные моменты и при этом выполняются условия:

а) М[ Х(t) ] = m ; D[ Х(t) ] = ϭ² ;

b) K (t₁, t₂) = K (t₂ - t₁) = K ( t ) ,

т.е. математическое ожидание с.п. не зависит от времени, а ковариационная функция не зависит от моментов времени t₁ и t₂ , а зависит лишь от разности

t = t₂ - t₁.