Основные характеристики случайных процессов

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

 

Основными характеристиками случайных процессов являются математическое ожидание, дисперсия, авто- и взаимная ковариационные ( или корреляционные) функции.

 

Определение: Математическим ожиданием случайного процесса Х (t)

называется неслучайная функция М[ Х(t)] = mx (t) , которая

для каждого фиксированного значения параметра t Î Т равна

математическому ожиданию соответствующего сечения и

вычисляется по формулам

 

,

 

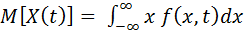если сечение с.п. - непрерывная случайная величина;

( 6 )

,

 

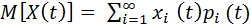если сечение с.п. - дискретная случайная величина.

 

Математическое ожидание с.п. Х(t) можно охарактеризовать как “среднюю”

функцию , около которой происходит разброс реализаций случайного процесса

( ярко выделенная линия на рис. 3).

 

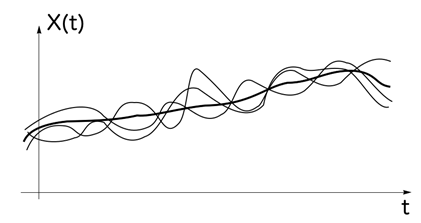
рис. 3

 

Определение: Дисперсией случайного процесса Х(t) называется неслучайная

функция D[ X(t) ] = Dx (t) = sx2, которая при каждом

фиксированном значении параметра tÎ T равна дисперсии

соответствующего сечения и вычисляется по формулам

 

M ,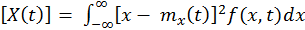

 

если сечение с.п. - непрерывная случайная величина;

(7)

,

 

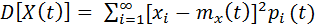если сечение с.п. - дискретная случайная величина.

 

Наиболее удобной для подсчета дисперсии является формула

 

D[ X(t) ] = М[ X2(t)] - M2[ X(t)]. ( 8 )

 

Если математическое ожидание М[ Х(t)] с.п. Х(t) представляет неслучайную “среднюю функцию”, около которой располагаются реализации с.п., то дисперсия D[ X(t) ] представляет собой неслучайную неотрицательную функцию, характеризующую степень разброса реализаций с.п. около своего математического ожидания.

Средним квадратическим отклонением sх(t) случайного процесса Х0(t) называется положительное значение корня квадратного из дисперсии D[ X(t) ] :

 

sх(t) = +Ö D[ X(t) ] .

 

Центрированным случайным процессом Х0(t) называется процесс, получаемый вычитанием из Х(t) его математического ожидания М[Х(t)]

 

Х0(t) = Х(t) - М[Х(t)]. ( 9 )

 

Используя определение математического ожидания с.п. и его свойства нетрудно показать, что М[Х0(t)] = 0.

 

Другой важной характеристикой с.п., определяющей степень линейной зависимости между сечениями Х(t1) и Х(t2) случайного процесса в различные моменты времени является ковариационная функция .

 

Определение: Корреляционной ( или автокорреляционной) функцией случай-

ного процесса Х(t) называется неслучайная функция Кх (t1, t2),

которая при каждой паре значений аргументов t1 и t2 равна

ковариации сечений Х(t1) и Х(t2) случайного процесса в

моменты времени t1 и t2

 

Кх(t1, t2) = М[Х0(t1) Х0(t2) ] = M[(Х(t1) - mx(t1)) (Х(t2) - mx(t2))] =

= M[Х(t1) Х(t2) ] - mx(t1)mx(t2) . ( 10 )

 

 

Корреляционная функция с.п. обладает свойствами:

 

1) при t = t = t корреляционная функция с.п. равна дисперсии случайного процесса

 

Кх(t, t) = М[ Х0(t) Х0(t) ] = M[ (Х(t) - mx(t))2 ] = D[ Х(t) ];

 

2) корреляционная функция с.п. симметрична относительно своих аргументов

 

Кх(t1, t2) = Кх(t2, t1);

 

3) корреляционная функция с.п. является положительно определенной, т.е. для любой произвольной функции a(t) ; tÎ T имеет место

 

òò a(t1) a(t2) К(t1, t2) dx1 dx2 ³ 0 ,

(В)

 

где В - подмножество Т.