Случайные функции. Случайные процессы.
Основные понятия и определения
Курс “Анализ случайных процессов” является разделом теории вероятностей и использует в своем изложении основные понятия, определения, свойства и теоремы из курса теории вероятностей.
Данный раздел высшей математики наиболее интенсивное развитие получил в начале ХХ века в связи с возросшим интересом к исследованию и построению математической модели броуновского движения, обнаруженного в 1827 г. английским ботаником Р. Броуном и заключающегося в том, что легкие частицы, взвешенные в жидкости, совершают беспорядочное движение. Для исследования процессов, аналогичных броуновскому движению, потребовался новый математический аппарат, дающий возможность количественного анализа не случайных величин, а случайных функций. Развитие электроники, радиотехники и космонавтики также способствовало совершенствованию теории и методов случайных функций, т.к. для создания сложных систем и управления ими требовался новый математический аппарат, адекватно описывающий поведение таких систем, находящихся в условиях постоянных случайных воздействий извне.
Поэтому естественно, что теория случайных функций, возникновение которой относится к началу ХХ века, в настоящее время является одним из наиболее быстро развивающихся разделов теории вероятностей.
На практике часто приходится решать задачи, связанные с определением вероятностных характеристик на выходе какой-либо системы при условии, что вероятностные законы входного воздействия (сигнала) известны при этом параметры системы могут быть как постоянными, не меняющимися во времени( в этом случае система называется детерминированной), так и изменяться случайным образом( в этом случае система называемся стохастической). Под вероятностными характеристиками случайных сигналов на входе и выходе исследуемой системы понимают функции распределения и (или ) функции плотности вероятностей, их числовые характеристики и ковариационные( или корреляционные) функции.
Случайные процессы, как объект исследования, возникают во многих задачах, имеющих практический интерес. В качестве примеров случайных процессов можно использовать показания термометра, отображающего суточную температуру в течение, например, одного месяца или года. Другим примером случайного процесса является амплитуда управляющего напряжения в кольце слежения либо за частотой, фазой или временной задержкой. Показания высотомера самолета также представляют собой случайный процесс.
В приведенных примерах показания термометра, высотомера самолета и амплитуда управляющего напряжения постоянно изменяются с течением времени, принимая случайные значения. Поэтому случайная функция характеризуется значением Х случайной величины x(t), принимаемым при произвольном неслучайном значении параметра t. Таким образом если задано некоторое множество Т действительных чисел и если каждому параметру tÎТ поставить в соответствие случайную величину x(w), то говорят, что на множестве Т задана случайная функция x(t,w) = Х(t) ; tÎТ, wÎW, ХÎХ.
Определение: Случайной функцией называется семейство случайных вели-
чин x(t,w), зависящих от параметра t, пробегающего заданное
множество Т.
Обозначение: Х(t) = x(t,w) = x t (w) ; tÎТ, wÎW, ХÎХ.
Если Т - подмножество прямой, а параметр t интерпретируется как время, то вместо термина “случайная функция” используют термин “случайный процесс”.
Наряду с названием “случайный процесс” ( сокращенно с. п.) в литературе встречаются эквивалентные термины - “вероятностный процесс”, “стохастический процесс”, которые выражают суть одного и того же.
При исследовании случайных функций( процессов) различают два случая:
1) аргумент случайной функции t может принимать любые значения в заданном интервале Т ( конечном или бесконечном);
2) аргумент t может принимать только определенные дискретные значения.
В первом случае Х(t) как правило называют случайным процессом; во втором - случайной последовательностью.
Например, текущие координаты цели, определяемые радиолокатором, вследствие ошибок измерения являются случайными функциями непрерывного времени, т.е. случайными процессами.
Не менее часты примеры, когда аргументом случайной функции является не время, а другой непрерывный параметр. Примерами здесь могут служить:
ордината волнового профиля поверхности моря для фиксированного момента времени как функция координаты точки моря; скорость ветра над заданной точкой земной поверхности как функция высоты рассматриваемой точки.
Для всех приведенных примеров случайных функций Х(t) = x(t,w)
характерно, что при фиксированном значении параметра t значения соответствующих функций являются случайными величинами x t (w); если же в функции Х(t) = x(t,w) зафиксировать элементарное событие w, то получим функцию х(t) = xw(t) - это неслучайная функция от tÎТ и называется выборочной функцией или траекторией ( реализацией) случайного процесса.
Совокупность траекторий { х1 (t), х2 (t), ... хn (t) } является случайным процессом Х(t) = x(t,w) " w i Î W.
Определение: Случайная величина x t (w) = Х( t0) при фиксированном
значении параметра t = t0 ÎТ называется сечением случайного
процесса.
На рис. 1 указаны сечения случайного процесса Х(t) в моменты времени t0, t1 и t2 , а также его различные траектории х1 (t), х2 (t), ..., х i (t), ..., хn (t).
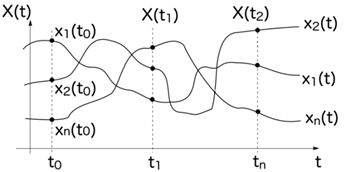
рис. 1
Совокупность всех сечений Х(t1), Х(t2), ... , Х(tn) случайного процесса Х(t) представляет собой многомерную случайную величину или случайный вектор
для всех ti Î Т. Таким образом случайный процесс это система случайных величин - всех сечений этого процесса.
Закон распределения системы случайных величин или случайного процесса задается многомерной функцией распределения
F( Х1, Х2, ... , Хn ) = Р { Х(t1)< Х1, Х(t2)< Х2, ... , Х(tn)< Х }. ( 1 )
Эти распределения при всевозможных t i Î T ; i = 1, n носят название конечномерных распределений случайной функции.
В качестве примера рассмотрим случайный процесс Х(t) , для которого сечение Х(t0) при любом фиксированном значении аргумента t = t0 представляет случайную величину с функцией распределения
F ( x; t0 ) = P { Х(t0) < х }. ( 2 )
Эта функция зависит от двух аргументов: во-первых от значения параметра
t = t0 , для которого берется сечение Х(t0) ; во- вторых от значения х , меньше которого должно быть значение, принимаемое случайной величиной Х(t0). Здесь функция (2) называется одномерным законом распределения случайного процесса Х(t) рис. 2.
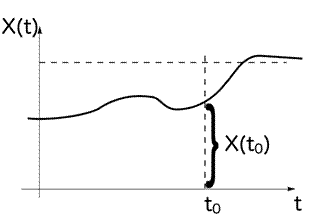
рис. 2
Соответствующая одномерная плотность существует , если сечение Х(t0) представляет непрерывную случайную величину, и в точках, где F ( x; t0 ) дифференцируема, справедливо равенство
¶F ( x; t0 )
f ( x; t0 ) = ¾¾¾¾¾¾ . ( 3 )
¶ x
Функция f ( x; t0 ) называется одномерной функцией плотности распределения вероятностей сечения случайного процесса в момент времени t = t0 .
Одномерные законы распределения F ( x; t0 ) и f ( x; t0 ) определяют вероятностное поведение ординат случайного процесса только в фиксированный момент времени t = t0 и ничего не позволяют сказать о значениях случайной функции в любой другой момент времени. Также функции F ( x; t0 ) и f ( x; t0 ) не отражают взаимной зависимости между значениями случайного процесса в различные моменты времени, что часто требуется в большинстве практических задач, например, в задачах прогнозирования ( или предсказания) случайных функций. Поэтому знание одномерных законов оказывается недостаточным и они не могут служить полной характеристикой случайного процесса.
Для получения более детальной характеристики случайного процесса рассматривают двумерные законы распределения:
F ( x1, x2; t1, t2 ) = P {x( t1) < x1 ; x(t2) < x2 } ; ( 4 )
¶2 F ( x1, x2; t1, t2 )
f ( x1, x2; t1, t2 ) = ¾¾¾¾¾¾¾¾¾ , ( 5 )
¶x1 ¶x2
где x( t1) и x(t2) - ординаты случайного процесса, являющиеся случайными величинами, соответственно в моменты времени t1 и t2 .
Здесь, как и прежде, двумерная плотность f ( x1, x2; t1, t2 ) существует , если случайный вектор { x( t1) ; x( t2) } является двумерной случайной величиной непрерывного типа, и если в точке (х1, х2) функция F(x1, x2; t1, t2 ) дважды дифференцируема, то имеет место соотношение ( 5 ).
Увеличение размерности законов распределения позволит получить еще более подробную характеристику случайного процесса и поэтому будем считать случайный процесс заданным, если заданы все многомерные законы распределения для любых значений t1, t2, ... , tn Î T, определяемые формулой (1).
В большинстве случаев на практике оказывается достаточным использование двумерных законов распределения. В частности, марковские процессы ( или процессы без последействия ), которые используют для описания процессов в радиоэлектронике, исчерпывающей вероятностной
характеристикой будет двумерный закон распределения, определяемый формулой ( 4 ).
Другой и важный класс случайных процессов - гауссовские ( или нормальные ) случайные процессы также полностью задается двумерным законом распределения ( 4 ).
Однако при исследовании случайного процесса для практических целей часто вообще отказываются от законов распределения вероятностей, а пользуются его основными характеристиками, которые описывают случайный процесс не полностью, а частично. Аналогично тому как числовые случайной величины позволяют в сжатой форме выразить наиболее существенные черты распределения случайной величины не подменяя при этом самого закона распределения. задаваемого функцией распределения.








