6. Составить канонические уравнения прямой
7. Составить уравнение окружности, имеющей центр в точке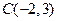 
и проходящей через точку 
.
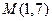8. Построить линию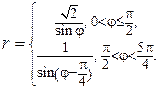 
9. Найти площадь параллелограмма, построенного на векторах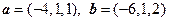 
.
10. Составить уравнение прямой, проходящей через точку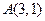 
перпендикулярно прямой 
.
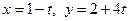11. Найти угол между плоскостями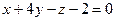 
и 
.
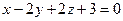12. Составить уравнения медианы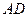 
треугольника с вершинами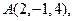 
.
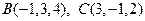13. Построить линию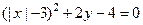 
.
14. Найти координаты вектора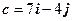 
в базисе 
.
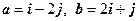15. Найти ориентацию тройки векторов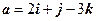 
, 
, 
.
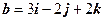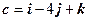16. Составить уравнение высоты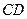 
в треугольнике с вершинами 
, 
, 
.
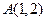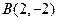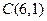17. A(0, 1, 1), В(–1, 2, 0), С(3, 0, 1). Составить уравнение плоскости, проходящей через точку пересечения медиан треугольника АВС параллельно плоскости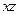 
.
18. Найти координаты точки пересечения прямой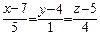 
с плоскостью 
.
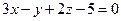19. Составить уравнение прямой, проходящей через точку (–2, 3) на одинаковых расстояниях от точек (5, –1) и (3, 7).
20. Составить уравнение плоскости, проходящей через точку (1, 1, –1) и перпендикулярной к плоскостям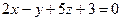 
и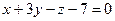 
.
21. Найти проекцию точки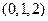 
на прямую 
.
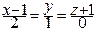22. Даны точк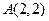и 
и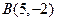 
. На оси абсцисс найти такую точку M, чтобы 
.
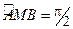23. Составить уравнение плоскости, проходящей через прямую 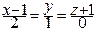и точку .
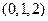24. При каком значении l плоскость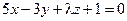 
будет параллельна прямой 
?
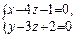25. Вычислить объем тетраэдра с вершинами в точках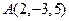 
, 
, 
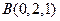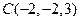и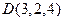 
.
26. Составить уравнение плоскости, проходящей через точк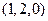и 
и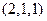 
перпендикулярно плоскости 
.
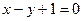27. Найти угол между прямой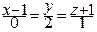 
и плоскостью 
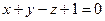и точку их пересечения.
28. 
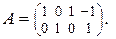
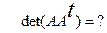
29. 
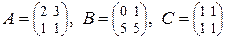. Решить уравнение 
.
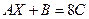30. Методом элементарных преобразований найти ранг расширенной матрицы системы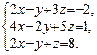 
31. Решить по правилу Крамера систему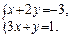 
32. Методом Жордана – Гаусса найти общее решение системы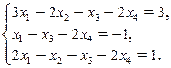 
33. 
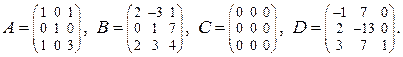
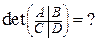
34. 
. 
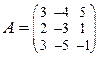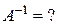
35. Методом элементарных преобразований найти ранг матрицы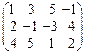 
.
36. Совместна ли система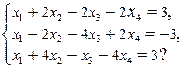 
37. Методом Жордана – Гаусса найти общее решение системы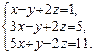 
38. 
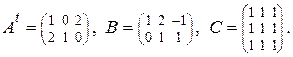
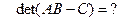
39. 
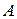– квадратная матрица четвертого порядка, 
, 
. 
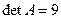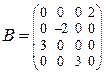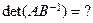
40. Решить по правилу Крамера систему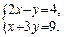 
41. Совместна ли система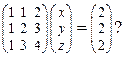 
42. Методом Жордана – Гаусса найти общее решение системы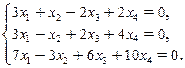 
43. Вычислить определитель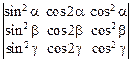 
.
44. Найти все значения параметра а, при которых система векторов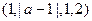 
, 
, 
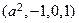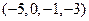линейно зависима.
45. Найти все значения параметра а, при которых система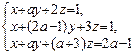 
совместна.
46. Вычислить определитель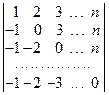 
порядка n.
47. Найти все значения параметра а, при которых система векторов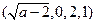 
, 
, 
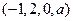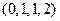линейно независима.
48. Найти все значения параметра а, при которых система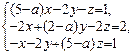 
несовместна.
49. Вычислить определитель 4-го порядка, в котором все элементы, стоящие на главной диагонали равны 0, а все остальные элементы равны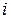 
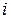( – мнимая единица).
50. Найти все значения параметра а, при которых система векторов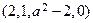 
, 
, 
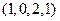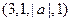линейно независима.
51. Найти все значения параметра а, при которых система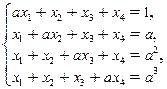 
совместна.