Пример 1. , , тогда фокус лежит на оси Ох. , тогда , и фокус лежит на оси Оу.
3.3. Линии второго порядка. 8
3.3.1. Окружность. 8
3.3.2. Эллипс. 8
3.3.3. Гипербола. 9
3.3.5. Парабола. 10
Линии второго порядка.
Определение. Кривой второго порядка называется линия, определяемая уравнением 2-ой степени относительно текущих координат x и у:
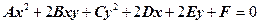
| (1) |
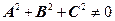 .
.
1. Окружность.
Определение. Окружностью называется геометрическое место точек, равноудаленных от одной заданной точки, называемой центром. При этом расстояние от любой точки окружности до центра называется радиусом.
Выведем уравнение окружности с центром в точке 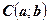 и радиусом
и радиусом 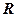 .
.
Расстояние от произвольной точки 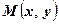 , принадлежащей окружности, до точки
, принадлежащей окружности, до точки 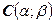 вычисляется по формуле
вычисляется по формуле 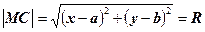 . Возведем обе части в квадрат и получим уравнение окружности с центром в точке
. Возведем обе части в квадрат и получим уравнение окружности с центром в точке 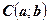
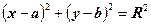
| (2) |
(2) - каноническое уравнение окружности.
2. Эллипс.
Определение. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.
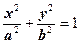
| (3) |
(3) – каноническое уравнение эллипса.
Если центром симметрии является не начало координат, а точка 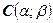 , то уравнение эллипса имеет вид
, то уравнение эллипса имеет вид
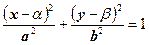
| (4) |
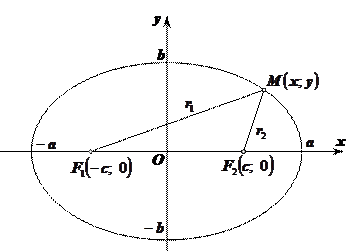
Фокусы эллипса расположены внутри(!!!) на большей оси.
а – большая полуось,
b – меньшая полуось,
2a – большая ось,
2b – меньшая ось.
Если 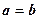 , то эллипс вырождается в окружность
, то эллипс вырождается в окружность 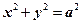 .
.
Пример 1. 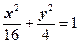
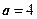 ,
, 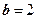 , тогда фокус лежит на оси Ох.
, тогда фокус лежит на оси Ох. 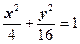 , тогда
, тогда 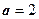 ,
, 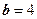 и фокус лежит на оси Оу.
и фокус лежит на оси Оу.
3. Гипербола.
Определение. Гиперболой называется геометрическое место точек, для которых модуль разности расстояний от двух данных точек, именуемых фокусами, есть величина постоянная, меньшая чем расстояние между фокусами.
Для вывода уравнения гиперболы введем на плоскости прямоугольную систему координат так, чтобы фокусы гиперболы лежали на оси абсцисс, а начало координат делило бы расстояние между фокусами пополам.
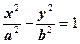
| (6) |
(6) – каноническое уравнение гиперболы.
Если центром симметрии будет точка 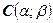 , то уравнение гиперболы имеет вид
, то уравнение гиперболы имеет вид
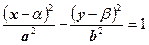
| (7) |
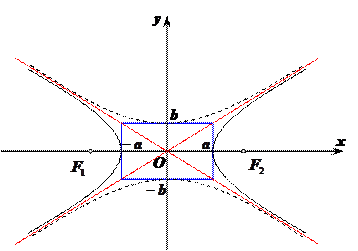
а – действительная полуось,
b – мнимая полуось,
2a – действительная ось,
2b – мнимая ось.
Фокусы гиперболы лежат за пределами основного прямоугольника.
Гипербола с равными полуосями 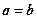 называется равносторонней.
называется равносторонней.
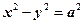 .
.
Пример 1. Построить кривую 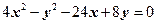 .
.
Решение. Выделим полные квадраты при х и у.
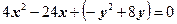
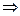
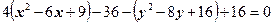
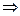
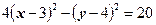
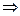
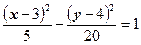 - гипербола с центром симметрии
- гипербола с центром симметрии 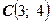
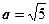 ,
, 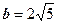
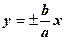
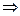
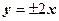 - асимптоты.
- асимптоты.
4. Парабола.
Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом. И от данной прямой, называемой директрисой и не проходящей через фокус.
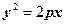
| (9) |
(9) – каноническое уравнение параболы. Так как уравнение (9) содержит у в четной степени, то парабола симметрична относительно оси Ох. Поэтому достаточно изучить лишь ее часть, лежащую в верхней полуплоскости. Решим уравнение (9) относительно у:
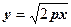
| (10) |
Точка О называется вершиной параболы, ось Ох – осью параболы. Параметр 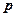 выражает расстояние от фокуса до директрисы. Посмотрим как он влияет на форму параболы. Предположим,
выражает расстояние от фокуса до директрисы. Посмотрим как он влияет на форму параболы. Предположим, 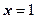 , тогда
, тогда 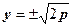 , получаем 2 точки на параболе:
, получаем 2 точки на параболе: 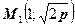 ,
, 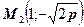 симметричные относительно ее оси. Расстояние между ними равно
симметричные относительно ее оси. Расстояние между ними равно 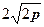 и чем больше р, тем больше это расстояние. Таким образом параметр р характеризует «ширину» области, ограниченной параболой. В этом и заключается геометрический смысл параметра р.
и чем больше р, тем больше это расстояние. Таким образом параметр р характеризует «ширину» области, ограниченной параболой. В этом и заключается геометрический смысл параметра р.
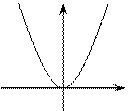
Частные случаи:
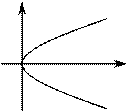
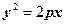
| 
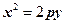
|
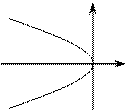
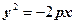 , , 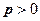
|
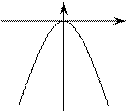
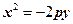 , , 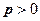
|
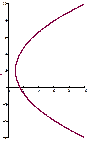
Если вершина параболы находится в точке 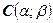 , то она описывается уравнением
, то она описывается уравнением
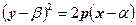 .
.
Пример. 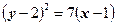
Решение. Вершина параболы находится в точке 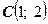 ,
, 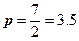
Задание.
1. Привести уравнение кривой 2-го порядка к каноническому виду, определить кривую и построить график:
2 х2- 6 х + 4 у2 + 3 у – 8 = 0 .








