Что такое анализ данных?
Уделим немного времени самому термину «анализ». Он происходит от древнегреческого ἀνά [ana] + λύω [luō], что означает «освобождать», «распутывать». В этом есть смысл, но слишком высокопарный, чтобы помочь нам уловить, что это действительно означает. Для целей бизнеса можно воспользоваться определением Марио Фариа из главы 1:
Анализ — преобразование данных в выводы, на основе которых будут приниматься решения и строиться действия с помощью людей, процессов и технологий.
Давайте остановимся на этом подробнее. Надеюсь, из главы 2 и главы 3 у вас уже сложилось понимание, что такое массив данных, а вот что такое аналитические выводы?
Согласно «Википедии», аналитические выводы — понимание конкретных причин и следствий в конкретном контексте[74]. В английском языке у этого термина (insight) есть несколько сопутствующих значений:
• информация;
• «озарение» — понимание внутренней сути вещей и процессов;
• самоанализ;
• проницательность, способность делать глубокие наблюдения и выводы;
• понимание причин и следствий на основе установления взаимосвязи и поведения в рамках модели, контекста или сценария.
Итак, понимание взаимосвязи причин и следствий, понимание внутренней природы вещей и процессов и так далее. Это будет нам полезно.
Термин «информация»[75], то есть «результат обработки данных для придания им контекста и смысла», часто используется как синоним термина «данные», хотя технически это не одно и то же (см. ниже врезку, а также статью The Differences Between Data, Information and Knowledge («Разница между понятиями “информация”, “данные” и “знания”»)[76].
ДАННЫЕ, ИНФОРМАЦИЯ И ЗНАНИЯ
Данные представляют собой сырые, необработанные факты об окружающем мире. Информация — собранные, обработанные данные, в то время как знания — это набор ментальных моделей и убеждений об окружающем мире, который сформировался на основе информации, полученной на протяжении какого-то периода времени.
Температура на данный момент составляет 6 °C. Это количественный факт. Он существует и соответствует действительности вне зависимости от того, зафиксировал ли его кто-то. К сожалению, этот факт бесполезен (для всех, кроме меня), так как из-за отсутствия контекста (когда? где?) он не позволяет сделать никаких выводов.
В Нью-Йорке 2 ноября 2014 года в 10 утра температура составила 6 °C. У этих данных есть контекст. Однако это по-прежнему лишь констатация факта без интерпретации.
Температура 6 °C гораздо ниже климатической нормы. Это информация. Мы обработали данные и объединили их с другими данными, чтобы определить понятие климатической нормы и оценить, как соотносятся значения.
При температуре 6 °C на улице прохладно, я надену пальто. Вы объединили информацию за какой-то период времени и построили мыслительную модель, что это означает. Это знания. Конечно, все эти модели относительны. Например, житель Аляски может посчитать температуру 6 °C в ноябре не по сезону теплой.
Исходя из глубины информации, мы вновь можем вернуться к подробному определению анализа (рис. 5.1). Хотя в нем по-прежнему остаются такие термины, как «понимание» и «контекст», надеюсь, теперь у вас более четкое представление о том, что такое анализ, по крайней мере концептуально. На этом новом уровне понимания давайте изучим набор инструментов, находящийся в распоряжении аналитиков. Сейчас речь идет не о программных инструментах, таких как Excel или R, а о статистических инструментах и о видах анализа данных, которые можно проводить.
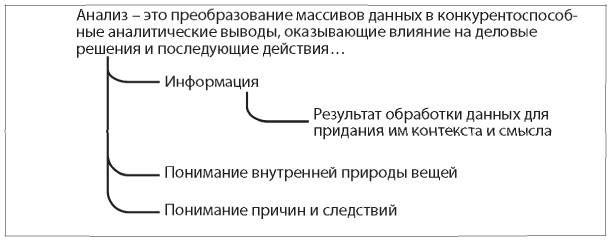
Рис. 5.1. Результат двухуровневого раскладывания определения термина «анализ»
Виды анализа данных
Джеффри Лик, старший преподаватель биостатистики в Университете Джонса Хопкинса, а также один из редакторов блога о статистике[77], выделяет шесть типов анализа данных[78]. Они перечислены далее от простого к сложному:
• описательный (descriptive);
• разведочный (exploratory);
• индуктивный (inferential);
• прогностический (predictive);
• каузальный (причинно-следственный) (causal);
• механистический (mechanistic).
Мы рассмотрим первые пять типов анализа. Механистический тип в большей степени связан с фундаментальной наукой, исследованиями и разработками, и к нему больше подходит термин «моделирование», чем «анализ». Механистическое моделирование и анализ отличаются очень глубоким пониманием системы, которое приходит в результате многолетнего контролируемого изучения стабильной системы посредством большого числа экспериментов. Именно на этом основана моя ассоциация с фундаментальной наукой. Это редкость для большинства компаний, за некоторыми исключениями, такими как научно-исследовательские подразделения фармацевтических компаний и инженерно-проектные подразделения технических компаний. Иными словами, если вы проводите анализ данных на этом уровне, который представляет собой вершину анализа, то практически наверняка вам не требуется читать в этой книге, как его выполнять. Если вернуться к главе 1, то сейчас у вас должен прозвучать звоночек. Ранее мы говорили о восьми уровнях аналитики. Сейчас мы говорим о шести типах анализа данных, при этом у нас встретилось всего одно общее слово — «прогностический». Что все это значит?
В предыдущем списке перечислены типы статистического анализа. Важно отметить, что они могут относиться к разным уровням аналитики. Например, на основе разведочного анализа данных (о котором шла речь в главе 2) можно подготовить ad hoc отчет (уровень аналитики 2). Также на его основе можно сформулировать бизнес-логику для системы оповещения (уровень аналитики 4), например определить 98-й процентиль в распределении и установить сигнал оповещения, если соответствующий показатель превысит этот уровень.
На рис. 5.2 показана попытка соотнести эти два списка: уровни аналитики (по вертикали) и пять типов анализа данных (по горизонтали). Интенсивность цвета каждой ячейки обозначает примерную оценку усилий или времени, затраченных на проведение этого типа анализа. Например, подготовка стандартных отчетов обычно осуществляется на основе описательного и разведочного типов анализа, при этом крайне маловероятно использование причинно-следственных моделей. С другой стороны, аналитика оптимизации строится на описательном и разведочном анализе, но в первую очередь сосредоточена на прогностическом и, возможно, причинно-следственном анализе.
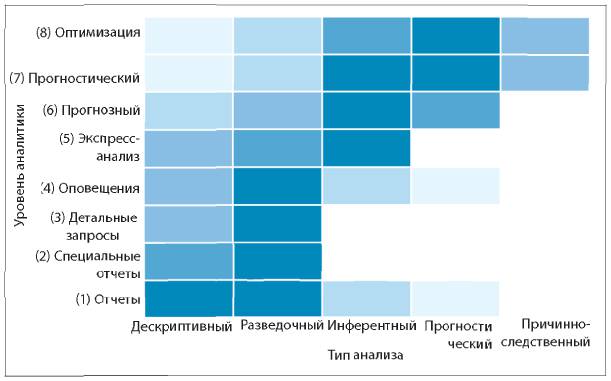
Рис. 5.2. Примерное соотношение между уровнем аналитики (по вертикали) и типом анализа (по горизонтали). Объяснение см. в тексте
Необходимо прояснить один момент. Существует множество других видов количественного анализа, например анализ выживаемости, анализ социальных сетей, анализ временных рядов. При этом каждый из них связан с конкретной областью профессиональных знаний или типом данных, а применяемые аналитические инструменты и подходы включают в себя шесть более общих аналитических инструментов и подходов. Например, при анализе на основе временных рядов можно вычислить период действия явления (описательный анализ), затем определить переменную во времени (разведочный анализ) и, наконец, смоделировать и прогнозировать будущие показатели (прогностический анализ). Вы получаете общую картину. Иными словами, перечисленные шесть классов представляют собой архетипы анализа. Кроме того, есть другие типы качественного анализа. Например, анализ основных причин, метод «Пять “почему”» от Toyota[79] и методология «Шесть сигм». Принимая это во внимание, давайте рассмотрим пять типов анализа.
СЛОВАРЬ ТЕРМИНОВ
Вы еще не запутались во всех этих «показателях», «переменных», «значениях»? Не переживайте. Эти термины пересекаются, и насчет их определении нет согласия. Ниже представлены мои варианты.
Переменная (Variable)
Показатель, который склонен меняться со временем, пространством или единицами выборки. Например, «Допустим, переменная v = скорость движения автомобиля» или «Пол — категориальная переменная».
Измерение (Dimension)
Это переменная. В то время как термин «переменная» чаще используют ученые и программисты, для представителей деловых кругов больше характерно употребление термина «измерение». Измерение — переменная, характеризующая факты и количественные показатели, она может отражать параметр категории или времени, а также рейтинга, рэнкинга или числа. Например, вы можете проанализировать совокупный объем продаж (значение) относительно страны (измерение) или года (измерение) или же рассчитать процент отказов (значение) относительно пола (измерение). В моем представлении измерения, как правило, находятся на оси х, а показатели — на оси y.
Значение (Measure)
Количественный показатель какого-либо свойства объекта, например длина, или стандартная единица измерения. В области бизнес-аналитики этот термин обычно относится к функции (например, BMI) или агрегированному значению, например минимальное, суммарное или среднее значение количественных данных. Может рассматриваться в виде чистого или производного значения чего-либо.
Показатель (Metric)
Функция от двух или более значений (с точки зрения измерения) или просто значение (в функциональном смысле). Производное значение.
Статистический показатель (Statistic)
Определенный показатель какого-то свойства в выборке значений, например среднее арифметическое = 6,3. Это функция, примененная к набору числовых данных, которая представляет собой отдельное значение. Несколько сбивает с толку, что и сама функция, и итоговое ее значение — статистические показатели.
Ключевые показатели эффективности деятельности (Key performance indicator)
В контексте ведения бизнеса этот показатель связан с целью деятельности и/или некоторыми основными ценностями (подробнее о KPI мы поговорим в следующей главе). То есть этот показатель связан с целью бизнеса или стартовой точкой.
ОПИСАТЕЛЬНЫЙ АНАЛИЗ
Наиболее простой тип анализа данных — описательный (дескриптивный). Он обеспечивает количественное описание набора данных. Важно отметить, что этот тип анализа касается только выборки данных, по которой проводится анализ, и не описывает ту совокупность, из которой он взят. На основании описательного анализа часто формируются данные, которые отображаются в дашбордах, например количество новых пользователей за неделю или размещенных заказов с начала года (см. раздел «Дашборды» в главе 7).
Давайте начнем с одномерного анализа, то есть описывающего одну переменную (ряд или поле) из набора данных. В главе 2 мы уже обсуждали составление пятичисловой сводки, однако есть множество других возможных статистических показателей; их можно условно разделить на меры среднего уровня («середина» данных), меры рассеивания (разброса данных) и формы распределения. Ниже перечислены показатели, относящиеся к числу простейших, но при этом наиболее важных.
Размер выборки
Количество единиц (записей) в выборке данных.
Далее перечислены меры среднего уровня.
Среднее значение
Чтобы найти среднее арифметическое, нужно сложить все значения и разделить на их количество.
Среднее геометрическое
Этот показатель применяется для определения среднего значения при наличии мультипликативного эффекта, например сложных процентов со ставкой, меняющейся из года в год. Чтобы найти среднее геометрическое, нужно перемножить все значения и извлечь из них корень. Степень корня определяется количеством значений. Если вы получили 8 % в первый год, а затем по 6 % следующие три года, средняя процентная ставка составит 6,5 %.
Среднее гармоническое
Средним гармоническим называется число, обратное среднему арифметическому их обратных. Например, если вы доехали до магазина со скоростью движения 80 км/ч, а на обратной дороге попали в пробку и скорость вашего движения составила 32 км/ч, ваша средняя скорость составит не 56, а 47 км/ч.
Медиана
Медиана — 50-й процентиль.
Мода
Наиболее часто встречающееся значение.
К мерам рассеяния относятся следующие.
Минимум
Наименьшее значение в выборке (0-й процентиль).
Q1
25-й процентиль. Значение выборки такое, что одна четвертая остальных значений выборки меньше него.
Q3
75-й процентиль. Значение выборки такое, что одна четвертая остальных значений выборки больше него.
Максимум
Максимальное значение в выборке (100-й процентиль).
Межквартильный размах
Центральные 50 % данных, разность между третьим и первым квартилями.
Размах
Разница между максимумом и минимумом.
Стандартное отклонение
Наиболее распространенный показатель рассеивания значений случайной величины относительно ее математического ожидания. Вычисляется как квадратный корень из дисперсии. Измеряется в тех же единицах, что и сама случайная величина.
Дисперсия
Мера разброса значений случайной величины относительно ее математического ожидания. Вычисляется возведением стандартного отклонения в квадрат. Измеряется в квадратах единицы измерения случайной величины.
Стандартная ошибка
Вычисляется путем деления стандартного отклонения на квадратный корень размера выборки. Показывает ожидаемое стандартное отклонение среднего значения выборки, если бы мы повторно получали выборки такого же размера из того же источника генеральной совокупности.
Коэффициент Джини
Количественный показатель, изначально разработанный, чтобы показать степень неравенства при распределении доходов. Тем не менее его можно использовать более широко. Он равен половине ожидаемой абсолютной разницы между доходами двух случайно выбранных людей, деленной на средний доход.
Меры формы включают следующие.
Коэффициент асимметрии
Величина, характеризующая асимметрию распределения. Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен в противном случае. Число фолловеров среди пользователей сервиса Twitter характеризуется положительным коэффициентом асимметрии (см., например, отчет An In-Depth Look at the 5 % of Most Active Users[80] и статью Tweets loud and quiet[81]).
Коэффициент эксцесса
Мера остроты пика распределения случайной величины. У распределения с высоким коэффициентом эксцесса[82] острый пик и плоские хвосты. На это стоит обратить внимание при инвестировании, так как это означает вероятность более резких колебаний по сравнению с переменной с нормальным распределением.
Кроме того, мне кажется, что тип распределения также можно назвать полезной описательной статистикой. Например, нормальное распределение (распределение Гаусса), логарифмически нормальное распределение, экспоненциальное распределение и унимодальное распределение — обычные. Зная тип, а следовательно, и форму распределения, можно узнать его потенциальные характеристики (например, что в нем могут быть редкие, но сильно отклоняющиеся значения), понять логику процесса генерации данных, а также определить, какие еще показатели требуется собрать. Например, если распределение представляет собой ту или иную форму экспоненциального закона, как распределение фолловеров в Twitter, очевидно, что следует вычислить отрицательный показатель экспоненты, который представляет собой важный критерий.
Не все переменные — непрерывные. Например, пол и продуктовая линейка относятся к категориальным переменным. Таким образом, описательный анализ может включать таблицы частотности для разных категорий или факторные таблицы, подобные следующей.
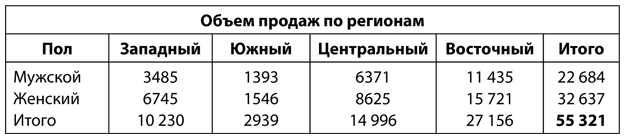
На этом уровне анализа проводящий его специалист должен знать, по какому критерию следует группировать данные, и понимать, когда какие-то данные выделяются из общей массы и представляют интерес. Например, в предыдущей таблице интересно, почему настолько велика доля женщин, совершающих покупки, в западном регионе.
При работе с двумя переменными описательный анализ может включать меры ассоциации, например вычисление коэффициентов корреляции и ковариации.
Цель описательного анализа состоит в числовом описании основных характеристик выборки. Он должен прояснять основные значения, отражающие распределение данных, кроме того, он может описывать взаимоотношения между переменными с показателями, описывающими ассоциации, или в сводных таблицах.
Некоторые из этих простых показателей могут оказаться весьма ценными сами по себе. Возможно, вам потребуется узнать и отследить среднее число заказов или наибольшую длительность их выполнения для разрешения практического вопроса с клиентом. Таким образом, этих данных может быть достаточно для составления стандартного и ad hoc отчетов, запроса или оповещения (уровни аналитики 1–4), и это может принести пользу компании. Кроме того, вы можете убедиться в качестве данных. Например, если максимальный возраст игрока, который зарегистрировался на сайте игры — «стрелялки» от первого лица, указан как 115 лет, то либо пользователь ошибся при вводе этой информации, либо в графе с датой рождения была установлена дата по умолчанию 1900 (ну, или это реально крутая бабушка). Помочь это определить могут простые минимум и максимум, размах выборки и гистограммы.
Наконец, описательный анализ обычно бывает первым шагом — возможностью познакомиться с данными — к более глубокому анализу.
РАЗВЕДОЧНЫЙ АНАЛИЗ
Описательный анализ — важный первый шаг. При этом просто итоговых цифр может быть недостаточно. Одна из проблем заключается в том, что большое число значений сводится к нескольким итоговым цифрам. А потому не стоит удивляться, что одни и те же итоговые статистические показатели могут описывать разные выборки с разным распределением данных, формами и свойствами.
На рис. 5.3 представлены две выборки с одинаковым средним значением, равным 100, но очень разным распределением.
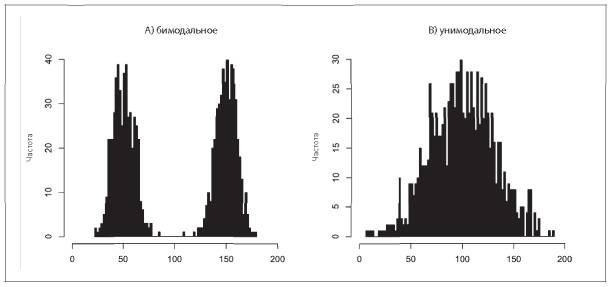
Рис. 5.3. А) бимодальное распределение и B) унимодальное распределение. В обоих случаях среднее значение одинаковое, примерно равно 100
Теперь это кажется не таким удивительным. У нас имеется простой итоговый статистический показатель — среднее значение одной переменной. Существует множество потенциальных «решений», или выборок, которым может соответствовать это значение.
Сейчас я покажу вам гораздо более удивительный пример. Предположим, у вас четыре набора данных с двумя переменными со следующими характеристиками.

Это система с жесткими заданными ограничениями. Значит, графики этих четырех наборов данных с идентичными статистическими характеристиками должны быть достаточно похожими, не так ли? А вот рис. 5.4 показывает, что это далеко не так.
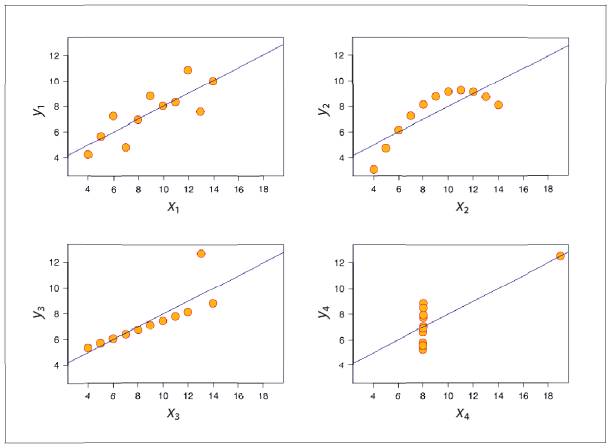
Рис. 5.4. Квартет Энскомба. В каждом из четырех наборов данных идентичны среднее значение х, среднее значение y, дисперсия х, дисперсия y, корреляция и прямая линейной регрессии (до двух знаков после запятой)
Источник: https://en.wikipedia.org/wiki/Anscombe’s_quartet
Это так называемый квартет Энскомба[83], названный по имени математика и статистика Фрэнсиса Энскомба, который составил его в 1973 году. Энскомб выступил против существовавшей на тот момент доктрины в области статистических вычислений, которая гласила, что:
1) числовые данные точные, а графики — приблизительные;
2) для каждого конкретного вида статистических данных существует только один набор вычислений, обеспечивающий правильный статистический анализ;
3) выполнение сложных расчетов — единственно верный путь, изучение данных только вводит в заблуждение.
Энскомб утверждал:
Большинство статистических вычислений строятся на предположениях относительно поведения данных. Эти предположения могут оказаться неверными, и тогда результаты вычислений тоже будут содержать ошибку. Всегда следует пытаться проверять, являются ли предположения верными. А если они ошибочны, мы должны быть способны понять, что с ними не так. В этом весьма полезны графики.
Применение графиков для визуализации и изучения данных получило название разведочного анализа данных. Наибольшую известность он приобрел благодаря продвижению американским математиком Джоном Тьюки в книге Exploratory Data Analysis (Pearson), опубликованной в 1977 году. При правильном подходе графики помогают видеть более масштабную картину, а также отмечать очевидные или необычные закономерности (это врожденное свойство человеческого мозга). Нередко аналитические выводы и понимание данных начинают формироваться именно на этом этапе. Почему у этой кривой такое отклонение? В какой момент наступает снижение возврата на маркетинговые расходы?
Разведочный анализ позволяет опровергнуть или подтвердить наши предположения относительно данных. Поэтому, когда в главе 2 шла речь о качестве данных, я рекомендовал использовать команду pairs() в среде R. Часто у нас сформированы обоснованные ожидания, что может быть не так с качеством данных, в отличие от ожиданий, какими должны быть достоверные данные.
По мере того как мы набираемся опыта и знаний в профессиональной области, у нас развивается интуитивное понимание, какие факторы и возможные отношения могут быть задействованы. Разведочный анализ, с его широким набором способов рассмотреть данные и их взаимоотношения, предлагает набор «луп» для изучения системы.
Это, в свою очередь, помогает специалисту по анализу данных выдвинуть новые гипотезы относительно того, что может произойти, если вы понимаете, какие переменные находятся под вашим контролем и какими рычагами вы можете воспользоваться для движения показателей, например выручки или конверсии, в нужном направлении. Кроме того, разведочный анализ способен показать пробелы в наших знаниях и определить, что можно сделать для их ликвидации.
Для одномерных непрерывных (действительные числа) или дискретных данных (целые числа) обычно строят диаграмму «стебель-листья» (рис. 5.5), гистограммы (рис. 5.6) и диаграммы размаха, или коробчатые диаграммы (рис. 5.7).
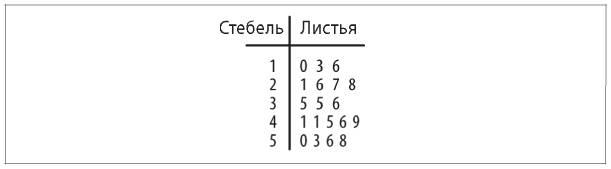
Рис. 5.5. Диаграмма «стебель-листья»
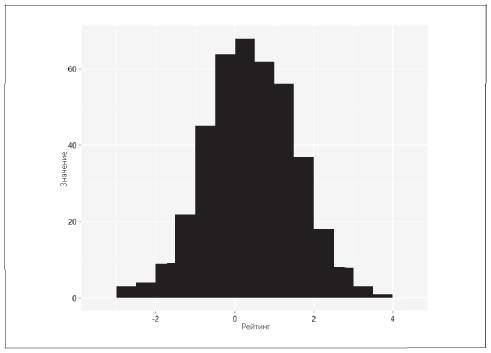
Рис. 5.6. Гистограмма
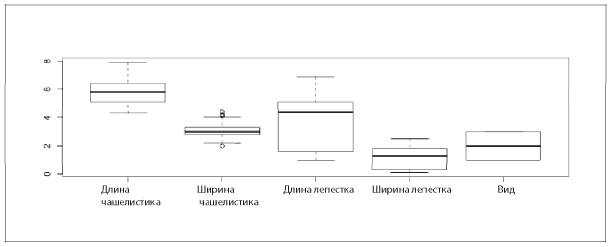
Рис. 5.7. Коробчатая диаграмма
Если гистограмма строится в таком масштабе, что ее площадь равна 1, это функция плотности распределения вероятностей.
Еще один полезный способ представить те же самые данные — составить интегральную функцию распределения.
Это может выделить интересные точки распределения, включая основные опорные точки.
На рис. 5.8, 5.9, 5.10 представлены основные графики для одномерных категориальных (качественных) переменных.
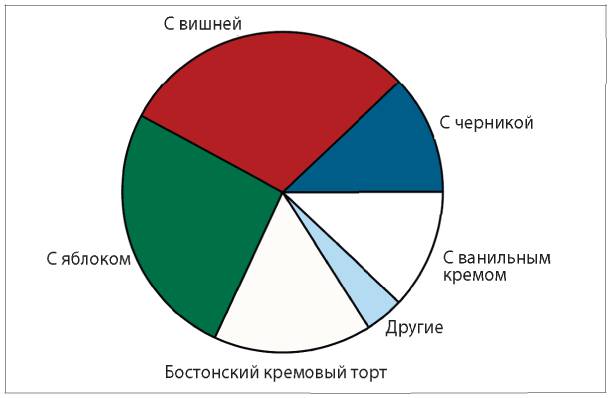
Рис. 5.8. Круговая диаграмма
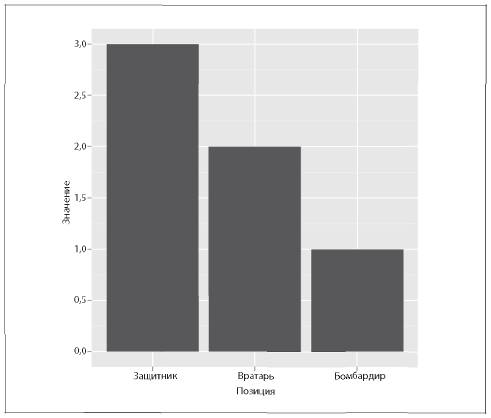
Рис. 5.9. Столбиковая диаграмма
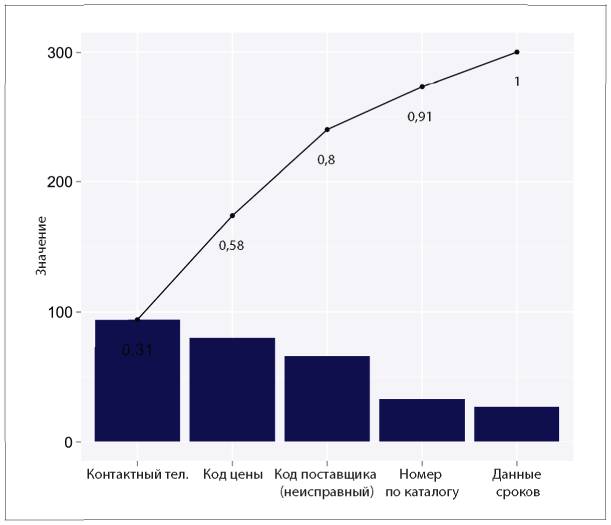
Рис. 5.10. Диаграмма Парето
Для визуализации двух переменных можно воспользоваться разными типами графиков.
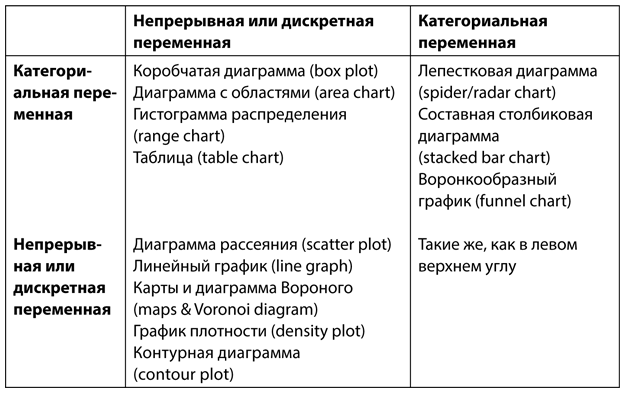
(См. также рис. 7.5.)
Есть целый набор графиков для одновременного изучения трех переменных. Некоторые из них более общие и привычные (график поверхности (surface), пузырьковая диаграмма (bubble plots), 3D-диаграмма рассеивания (3D scatter)), а некоторые применяются для особых целей (см. the D3 gallery[84]).
В случае, когда одна из переменных — время (например, годы) или категориальная переменная, также можно использовать подход небольших множеств (small multiples), при котором создается решетка из одномерных или двумерных графиков (рис. 5.11).
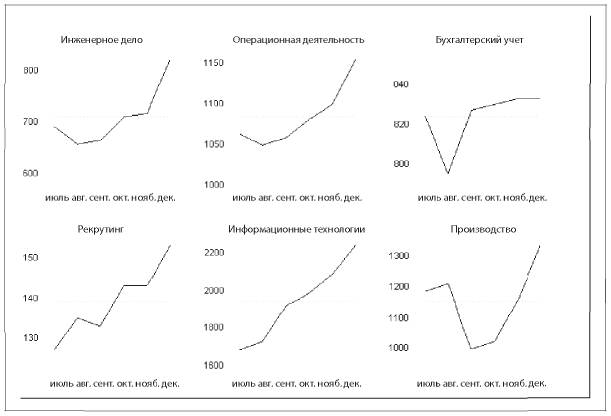
Рис. 5.11. Пример маленьких множеств
Источник: https://en.wikipedia.org/wiki/Small_multiple

Не ограничивайтесь использованием одного или двух типов диаграмм. Каждый из этих типов диаграмм выполняет свою задачу. Изучите их преимущества и недостатки и применяйте те из них, которые лучше всего отражают интересные сигналы, тренды или образцы. (Мы еще вернемся к некоторым из этих аспектов в главе 7.)
Там, где возможно, пользуйтесь командами, например pairs(), при автоматическом создании графиков и диаграмм для различных комбинаций переменных, которые вы можете быстро просмотреть в поисках интересных деталей или странностей, заслуживающих дополнительного внимания.








