Плоский точечный источник и сток
Рассмотрим комплексный потенциал
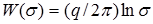, (1.26)
где q - некоторая постоянная величина.
Это уравнение представим в виде
,
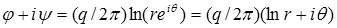где r - расстояние до точки с координатами х, у (полярный радиус); q - полярный угол.
Из полученного уравнения следует, что
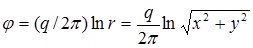; (1.27)
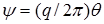. (1.28)
Из (1.27) находим, что радиальная составляющая скорости (по направлению радиуса r)
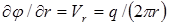, (1.29)
а составляющая по нормали к этому радиусу Vs =0.
 |
Таким образом, получили поток, линии тока (траектории) которого представляют собой семейства прямых, проходящих через начало координат (это же следует из уравнения линии тока y = const). Такой радиальный поток, идущий от начала координат, называется плоским точечным источником (рис. 1.2).
Рис. 1.2. Схема плоского точечного источника
Расход жидкости через контур радиуса r: 2 p rVr = Q . Внося сюда значение Vr из (1.29), найдем: Q = q . Следовательно, постоянная q определяется расходом жидкости из источника. Эта величина q называется мощностью или интенсивностью источника.
Наряду с источником существует вид движения жидкости, называемый плоским точечным стоком. Комплексный потенциал стока
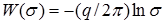. (1.30)
Знак минус указывает, что, в отличие от источника, движение будет происходить к центру. Сток, как и источник, характеризуется мощностью, или интенсивностью q (расходом в единицу времени).
Пространственный источник и сток
Помимо плоских существуют пространственные точечные источники (стоки). Поток от них задается следующими условиями:
; 
; 
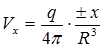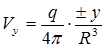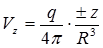, (1.31)
где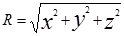 
, q - интенсивность источника (знак плюс) или стока (знак минус). Интенсивность источника (стока) равна величине q, определяемой как секундный расход через поверхность сферы радиусом R. Полная скорость
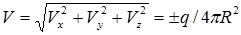(1.32)
и совпадает с направлением радиуса-вектора R. Поэтому потенциал скоростей зависит только от R и, следовательно:
.
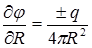После интегрирования
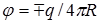, (1.33)
где знак минус относится к источнику, а знак плюс - к стоку.
Диполь
Рассмотрим поток, комплексный потенциал которого
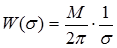, (1.34)
где М - постоянная величина. В соответствии с этим уравнением
.
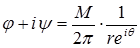Преобразуем правую часть этого равенства. Учитывая, что
,
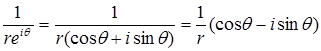получаем
.
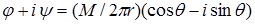Отсюда
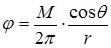, (1.35)
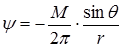. (1.36)
Полагая y = const и учитывая, что
; 
,
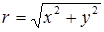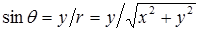получаем уравнение семейства линий тока рассматриваемого течения:
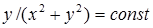. (1.37)
Семейство линий тока представляет собой бесчисленную совокупность окружностей, проходящих через начало координат и имеющих центры на оси у (рис. 1.3а).
Чтобы представить физическую картину этого течения, рассмотрим поток, который получается в результате сложения течений от источника и стока одинаковой интенсивности, расположенных на оси х на малом расстоянии e от начала координат (рис. 1.3б). Для точки М(х, у) потенциал скоростей потока от источника, расположенного на расстоянии r 1, jист=( q /2 p ) lnr 1, а от стока, расположенного на расстоянии r 2 этой точки, jст=(- q /2 p ) lnr 2 .
 |
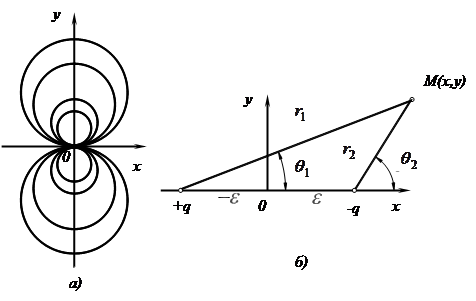Рис. 1.3. Схема определения диполя:
а - линии тока диполя, б - схема образования диполя
Чтобы определить суммарное течение от источника и стока, воспользуемся методом наложения несжимаемых потоков. По этому методу потенциал скоростей суммарного течения j = jист+ jст . Действительно, в силу уравнения неразрывности (уравнения Лапласа) [5], общий вид которого
,
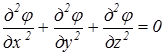получаем
.
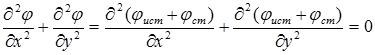Так как функции jист и jст удовлетворяют уравнениям
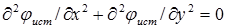и 
,
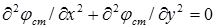то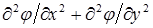 
тождественно равно нулю. Следовательно, суммарная функция j удовлетворяет уравнению неразрывности. Суммарный потенциал от источника и стока
.
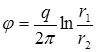Так как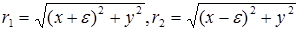 
, то
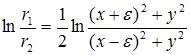, или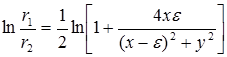 
.
Величину e можно выбрать такой, что второй член в скобках будет мал по сравнению с единицей. Применяя формулу разложения в ряд для логарифма и пренебрегая членами более высокого порядка малости, получим
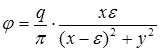. (1.38)
Пусть источник и сток сближаются (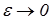 
) и одновременно с этим увеличиваются их мощности так, что произведение q 2 e в пределе при совмещении источника и стока стремится к некоторой конечной величине М. Образующийся при этом сложный поток называется дипо лем, величина М, характеризующая этот поток, — моментом диполя, а ось х — осью диполя. Переходя к пределу в (1.38) для j пр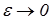и и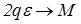 
, для диполя получаем выражение
,
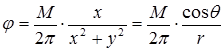совпадающее с (1.35). Таким образом, рассматриваемый поток, характеризующийся комплексным потенциалом (1.34), является диполем. Это же можно показать, если рассмотреть функцию тока такого совмещенного течения, которая будет совпадать с (1.36).
Осуществляя дифференцирование (1.35), определим составляющие скорости диполя:
, 
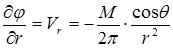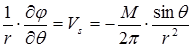. (1.39)
Рассмотрим пространственный случай. Для течения, созданного источником и стоком одинаковой интенсивности q , помещенными на оси Ох на малом расстоянии e от начала координат, потенциальная функция в соответствии с (1.33)
,
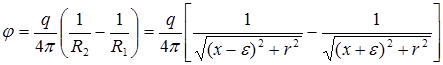где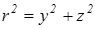 
.
Для малых значений e
.
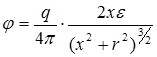Отсюда при переходе к пределу при 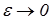, считая что произведение q 2 e стремится к конечному пределу М, получим для течения, созданного диполем с моментом М, потенциал скоростей
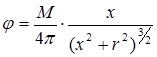, (1.40)
или
,
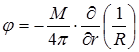где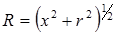 
.