Комплексный потенциал

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Движение безвихревого несжимаемого потока можно полностью определить, если известна потенциальная функция j или функция тока y, связь между которыми дается уравнениями (1.15), известными в теории функций комплексного переменного как уравнения Коши-Римана. Эти уравнения выражают необходимые и достаточные условия того, что комбинация из двух функций j + i y является аналитической функцией комплексного переменного 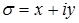, т.е. дифференцируемой во всех точках некоторой области.

Введем обозначение для этой функции:

W ( s )= j + i y . (1.16)

Функция W ( s ), которая определяется, если функция от двух действительных переменных j = j ( x , y ) и y = y ( x , y ) удовлетворяет дифференциальным уравнениям (1.15), называется комплексным потенциалом. Если значения функций j ( x , y ) или y ( x , y ) позволяют однозначно определить поле скоростей в движущейся жидкости, то, следовательно, любой двухмерный плоский поток может быть задан комплексным потенциалом. Отсюда задачу о расчете такого потока можно свести к нахождению функции W ( s ). Вычислим производную по комплексному переменному s от функции W( s ):

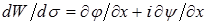. (1.17)

Так как 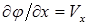, , 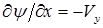то

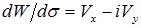. (1.18)

Это выражение называется комплексной скоростью, модуль которой дает величину самой скорости: 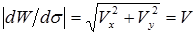. Очевидно, что действительный вектор скорости 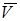= V_x + iV_y является зеркальным отображением относительно оси х вектора комплексной скорости. Обозначим q угол между вектором dW / d s и осью х и определим скорост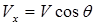и: и 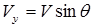. Используя формулу Эйлера:

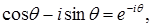
получаем

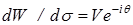. (1.19)

Виды потоков жидкости

Рассмотрим характерные виды потоков несжимаемой жидкости, их геометрическую картину (аэродинамический спектр), выражения для комплексных потенциалов, а также соот­ветствующих потенциальных функций и функций тока.

Плоскопараллельный поток

Пусть движение жидкости задано комплексным потенциалом

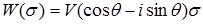, (1.20)

где V и q - некоторые величины, постоянные для данных условий.

В соответствии с (1.16)

,

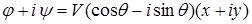откуда находим потенциал скоростей и функцию тока:

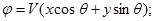(1.21)

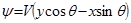. (1.22)

Из выражений для j или y следует, что рассматриваемый поток плоский и установившийся, так как время в них явно не входит. В таком потоке линии тока и траектории совпадают.

Из (1.21) можно найти составляющие скорости потока:

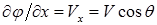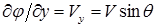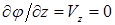, , . (1.23)

Здесь V - полная скорость потока, а q - угол между ее направлением и осью х. Приравнивая функцию тока y (1.22) к постоянной и включая в нее V, получаем уравнение

, (1.24)

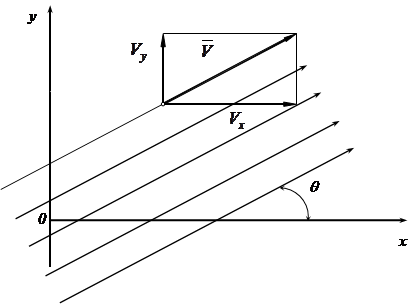из которого видно, что линии тока представляют собой параллельные прямые, наклоненные к оси х под углом q (рис. 1.1). Так как составляющие скорости V_x и V_y положительные, то направление потока будет таким, как показано на рис. 1.1. Такой поток называется поступательным плоскопараллельным.

Рис. 1.1. Общий вид поступательного плоскопараллельного потока

В частном случае, когда поток параллелен оси х (q=0, V_x = V , V_y =0), комплексный потенциал

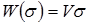. (1.25)